
Modeling Multi-agent Logistic Process System using
Hybrid Automata
Ammar Mohammed and Ulrich Furbach
Koblenz-Landau University, Computer Science Department, D-56070 Koblenz, Germany
Abstract. Multi-agent systems are a widely accepted solution to handle complex
problems. One application of multi-agent system is autonomous logistics. In au-
tonomous logistic processes, potentially every element in a logistic supply chain
is modeled as cooperating software agent. Thus, there exist modeling languages
that are used to model such multi-agent systems. However, these modeling lan-
guages do not allow verifying the properties of systems. Hybrid automata can be
used to model hybrid systems by capturing both discrete and continuous changes
of a system. Fortunately, hybrid automata are equipped with formal semantics
that make formal methods possible to apply to them in order to prove certain
properties of the specified systems. In this paper, we model multi-agent system
behaviors in autonomous logistic processes using the concept of hybrid automata.
With the help of model checking techniques, we can prove some properties of a
modeled system before involving in the implementation of a system.
1 Introduction
Software agents and multi-agent systems (MAS) are an approach to implementing au-
tonomous and interacting software systems. An agent is an autonomous decision maker
on behalf of some real world entity. Generally, agents are able to perceive from their
environment with sensors, and to act with actuators. The agents choose their action
as because of a reasoning process. In particular, agents in multi-agent system are able
to communicate and coordinate with each other to fulfill tasks in cooperation or com-
petition depending on their respective goals and abilities. This enables them to solve
complex problems and tasks in a distributed way [9] .
There are severalapproaches for modeling multi-agent system like [11], [12]. Among
of them, Agent UML [1] is one of the widely accepted languages for modeling multi-
agent system . This language is chosen by FIPA
1
association as an acceptable language
to model interactions among agents. Unfortunately, although most multi-agent system
modeling languages are clear to understand, they are not able to verify some properties
of the modeled system, because there is no formal semantics of agent decision making.
One important aspect of multi-agent systems is that the agents interact with a physi-
cal environment. Such interactions typically consist of continuous changes of behaviors
of an agent (e.g. a movement of an agent in logistic transportation, or an agent waiting
for some events), as well as discrete changes of the behaviors. The previous scenario
1
www.fipa.org
Mohammed A. and Furbach U. (2008).
Modeling Multi-agent Logistic Process System using Hybrid Automata.
In Proceedings of the 6th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages
141-149
DOI: 10.5220/0001729501410149
Copyright
c
SciTePress

can be captured using hybrid automata [7]. In hybrid automata, the discrete changes are
modeled using state chart, while the continuous changes are modeled using differential
equations. Fortunately, hybrid automata are equipped with formal semantics that make
them accessible to formal validation of modeled behaviors. Thus, it becomes possibly
to prove desirable features as well as to prove absence of unwanted properties for the
modeled behavior automatically with the help of model checking methods.
To this end, the aim of this paper is to model a multi-agent system scenario in au-
tonomous logistic processes using hybrid automata and by using model-checking tech-
niques [2], we can prove certain properties of the modeled system. Each agent in the
involvedscenario is described using Hybrid automaton and the communication between
agents is represented using shared variables and synchronization labels. However, be-
fore we begin describing the subsequent sections, we will use the term Automaton and
Agent synonymously. The remainderof this paper is divided as follows. Section 2 shows
the concept of hybrid automata. In section 3, we will discuss autonomous logistic pro-
cess and our proposed model scenario. Section 4 comes with verifying some properties
of the modeled scenario. Finally, section 5 concludes the paper.
2 Hybrid Automata
A hybrid system is a system with a phased evolution. Within each phase, the system
evolves continuously according to a dynamic law. When an event occurs, the system
makes a discrete transition from one phase to the next. A non-deterministic automaton
can be used to describe the discrete behavior, and the continuous behavior within each
phase can be described by a differential equation. This leads to the notion of hybrid au-
tomaton. Hybrid automata have been introduced as a formal model for hybrid systems
that combine discrete control graphs, usually called finite state automata, with continu-
ously evolving variables. The syntax of hybrid automata is defined as follows, and for
more detail, you can see [7].
2.1 Formal Definition
A hybrid automaton A is a tuple (X,V,F,I,Init,E,Jump,
P
,Syn) where:
– X is a finite set of n real-valued variables. For example, the variable Tdistance
,in the automaton truck Fig. 1, represents the speed of a truck inside the automaton.
– V is a finite set of locations. For example, the automaton Fig.2 has locations, named,
Begin,Goodcondition, Badcondition,and Finish.
– F is the flow function which maps set of locations V to predicate over X
S
˙
X, where
˙
X is the set of differential equations of the set of variables X. When the control of a
hybrid automaton A is at location v∈V, the variables evolve according to differen-
tiable functions, which satisfy the flow conditions F at this location. For example,
location GoodCondition, in Fig.2, has a flow condition denoted as F:
˙
envT ime=1.
A flow may be omitted if nothing changes continuously.
– I is the invariant that is a mapping from the set of locations V to the predicate over
the variables in X. I:v means the invariant condition at location v,and it permits
142

that the control will be at location v, whenever the condition is true. For instance,
the location GoodCondition Fig.2 has invariant I:envTime≤gtime, which
means that the control will be at this location until the condition is violated. The
invariant I:True means that the invariant is always achievable at the respective
location.
– Init Is a mapping from the set of locations V to the predicate over X that repre-
sents the initial condition at each location. Init(v) is called the initial condition of
location v. Initial conditions, graphically, are expressed as incoming arrow marked
with condition in an automaton. For example, envTime=0 represents the initial
condition at location GoodCondition Fig.2.
– E is a finite set of edges, called transition. A transition e=(v,
´
v) is a directed edge
between a source location v ∈ V and target location
´
v ∈ V.
– Jump is a mapping, which assigns to each edge e∈E a jump condition. If the jump
condition a transition e∈E holds, the transition e can take place and may change
the values of the variables X by executing a specific action (assignment). For in-
stance, the transition between GoodCondition and BadCondition (Fig.2)
has a jump condition envTime=gtime, and when it holds it updates the value of
the variable envTime to the value 0 using envTime:=0.
–
P
is a finite set of synchronization labels and a labeling function Syn that assigns
each transition e∈E a synchronization label from
P
. The synchronization labels
are used to define the parallel composition of two automata. If both automata share
the same synchronization label s∈
P
, then each s-transition of one automaton must
be accompanied by s-transition of the other automata. For example, both truck and
environmentautomaton (see Fig.1 and Fig. 2) share the same synchronizationlabels
Tobad, Done, and ToGood.
2.2 Parallel Composition
Parallel composition of hybrid automata can be used for specifying larger systems. A
hybrid automaton is given for each part of the system, and communication between the
different parts may occur via shared variables and synchronization labels. Technically,
the parallel composition of hybrid automata is obtained from the different parts using
a product construction. The transitions from the different automata are interleaved, un-
less they share the same synchronization label. In this case, they are synchronized the
execution simultaneously. In our scenario, the system is built using the parallel com-
position of four automata, two trucks, environment, and cargo automaton, as
we will show in the next sections.
3 Autonomous Logistic Processes
Getting the right goods to the right place at the right time are the requirements on lo-
gistics. Nevertheless, with highly dynamic markets and increasingly complex logistic
networks it is becoming more and more difficult to meet these standards with con-
ventional methods of planning and control. In the future, aspects such as flexibility,
adaptability and reactivity will be of primary importance. The paradigm of autonomous
143

logistic processes [10] addresses these aspects by decentralizing logistic control to sin-
gle logistic entities (e.g. freight items, transport containers, means of transport, or stor-
age facilities). Therefore, autonomous logistic processes aim at managing logistics in
a highly distributed way by transferring decision-making competencies to the logistic
entities. MAS is an adequate and promising technique to implement the autonomous
logistic process [5]. Logistic entities as well as secondary logistic services (e.g. traffic
information, route planning, and service brokerage) are represented by software agents
interacting with each other to coordinate the logistic process. Agent communication and
coordination follows standards defined by FIPA association, i.e., using Agent Commu-
nication Language (ACL) and interaction protocols for specific agent conversations.
In the next subsections, we will describe a multi-agent system in logistic scenario and
show how this can be modeled with hybrid automata.
3.1 Case Study: Logistic Process Scenario
Our multi-agent scenario constitutes four agents: cargo, environment, and two trucks.
The cargo has the objective to be transported to some destination city. The trucks may
offer transportation service. Additionally, the environment agent represents an external
disturbance to the transportation process. In the following, we will discuss the scenario
in more details.
Initially, the cargo tries to contact the two different trucks for requesting the trans-
portation service. The two trucks are located in two different cities. When the cargo
calls for a proposal, it sends information, including destination point of the shipment,as
well as its due time (deadline), to trucks. As soon as each truck receives the call for
proposal, it evaluates and estimates this request according to decision criteria (e.g. its
speed limit, transport distance, deadline for transportation). The reason behind the es-
timation and evaluation processes is that the truck has to check if it may perform the
transportation due to some constraints like (the delivery not after deadline). If it can
offer transportation, it accepts the proposal and proposes its desired price. On the other
hand, if the cargo received multiple proposals, it can pick up the one, which has the
lowest price.
Once a selected truck begins the process of transportation, it may be exposed to
some environment condition (un-anticipated environmental interactions e.g. traffic or
bad weather, etc.). For simplicity, we will use two different environment conditions;
named bad and good conditions. These conditions influence the speed of the truck ac-
cording to their state (i.e. bad or good). The truck slows down its speed to its min-
imum limit, whenever it is subjected to a bad condition received from the environ-
ment, whereas it accelerates to its maximum limit, whenever environment conditions
are good. The influence of the environment is of course seriously limited in this way.
In reality, these conditions are more complex than our scenario. In a more realistic
model of the environment, a stochastic characterization of disturbances would be used.
Stochastic models, however, go beyond the expressiveness of hybrid automata. At the
end of the transportation process, the truck reports its delivery time with comparison
to the due time. Therefore, if the truck delivered the shipment after the deadline, it in-
forms the cargo with failure in the transportation otherwise, it informs the cargo that the
transport was successful.
144
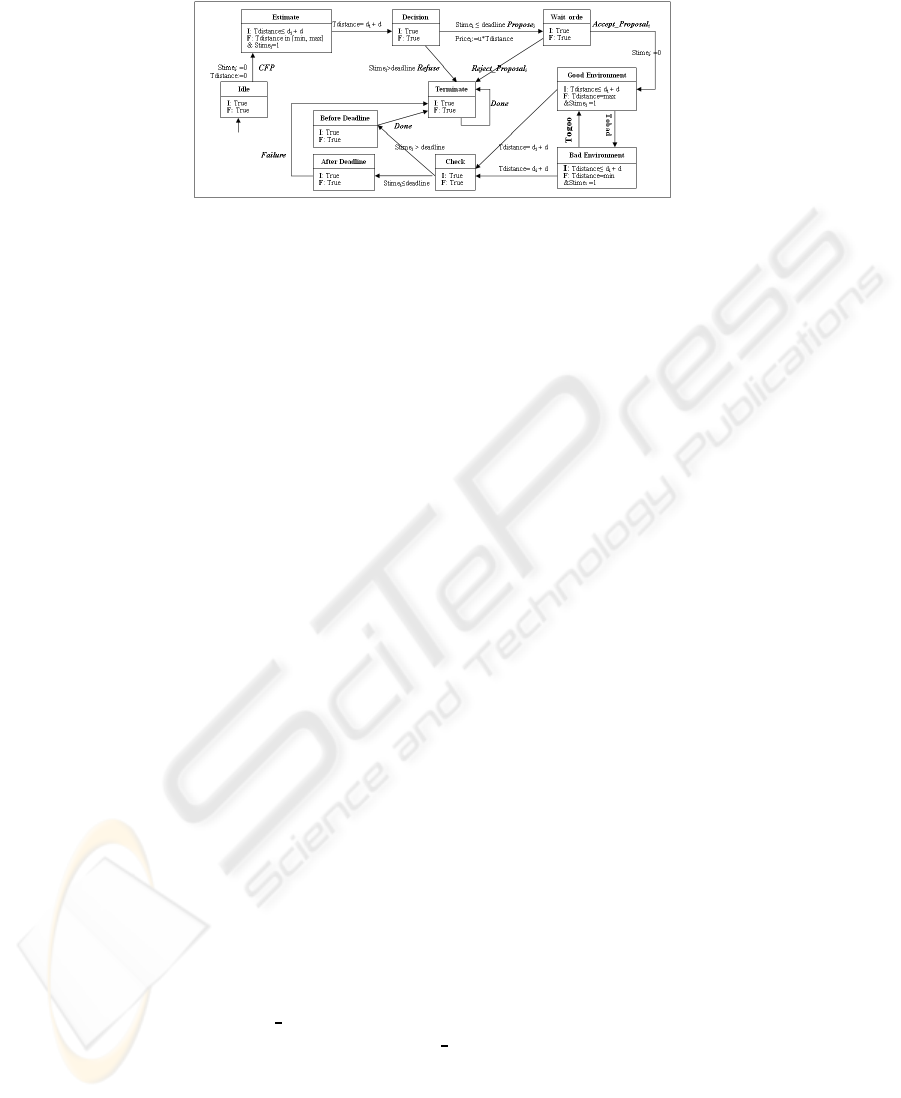
Fig.1. Truck Automaton.
Surely, the previous scenario can be modeled using FIPA contract net protocol
[3]. As we mentioned before, FIPA specification gains widely acceptance in model-
ing multi-agent system especially for representing the interactions among the agents.
It lacks, however, from proving certain properties to the modeled multi-agent system.
Therefore, we intend in the next sections to model the previous scenario using hybrid
automata, and with the help of model checking we check desirable features.
3.2 The Model
As stated earlier, hybrid automata allow to model systems as a set of concurrent pro-
cesses. We model the logistic scenario described in the previous section as a concurrent
hybrid automata. Each automaton represents an agent in the modeled scenario. Truck
automaton, cargo automaton, and environment disturbance automaton will be described
in the following subsections in more details.
Truck Automaton. Figure 1 depicts the automaton(agent) truck. In our scenario, we
have two trucks with the same behaviors, but with different capabilities (e.g. speed,
price, total distance the truck will pass). Each truck has desired price to perform the
transportation, and has different speed capability.
Initially, the behavior of a truck control starts at location Idle, and waits for in-
coming proposal from the cargo. The proposal is represented by the synchronization
label CFP. Once a truck receives a CFP message, the control goes to location Esti-
mate. At the later location, the truck estimates, according to its minimum and maxi-
mum speed limit,as well as, the expected time it will take to perform the transportation
process. Once the estimation process terminates, the control goes to location Decision
. From this location, the control goes to either location Terminate or Wait-order. The
former location is chosen whenever the expected estimation time exceeds the deadline
for transporting the shipment. However, if it goes to Wait-order, the truck proposes to
perform the transportation as well as the intended price. From location Wait-order, the
control goes to either location GoodEnvironment or Terminate. This is depending on
the received message from the cargo. The control goes to location Terminate; when
the truck receives proposal rejection from the Cargo (which is represented by synchro-
nization label Reject proposal in Fig. 1). However, when the truck receives ac-
cept proposal(indicated in Fig.1 as Accept proposal), the control goes to location
GoodEnvironment and the control mutually changed between GoodEnvironment and
BadEnvironment according to the influence of the environment to the truck. The truck
145
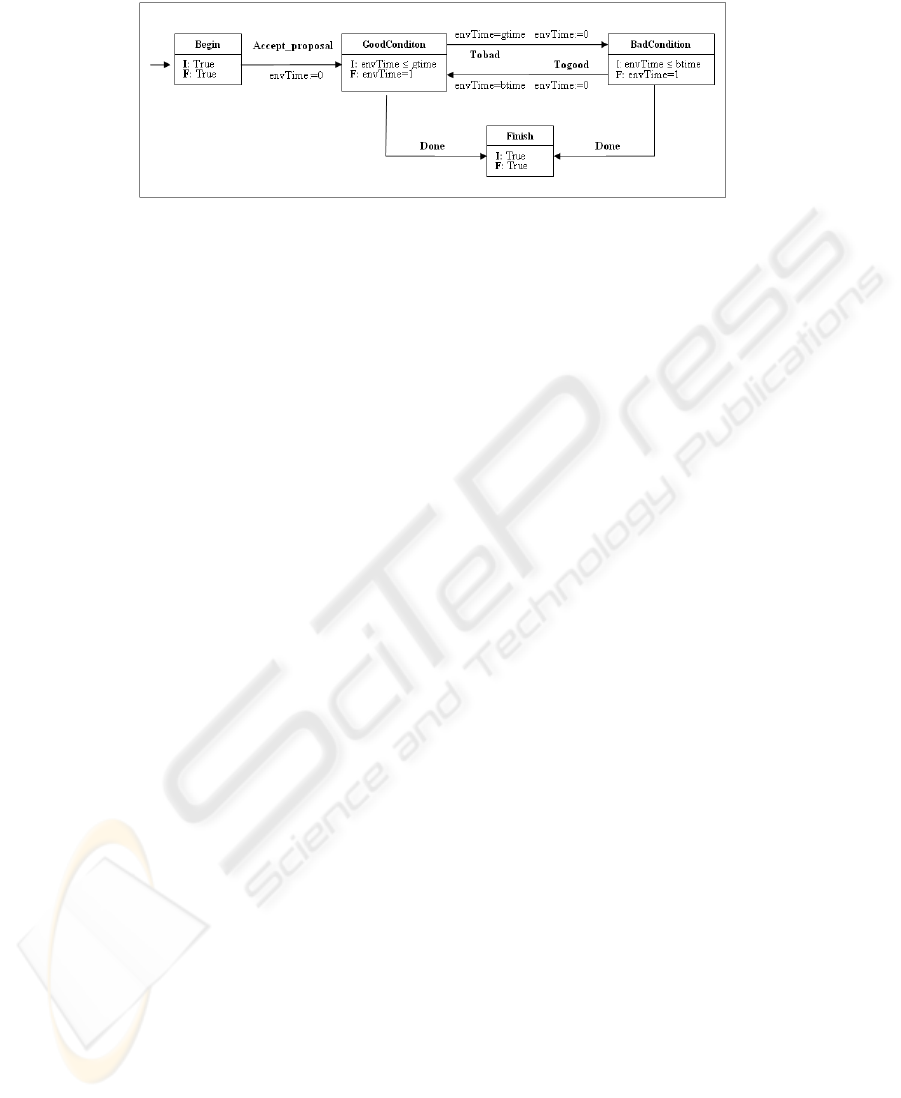
Fig.2. Environment Automaton.
receives disturbance from the automaton environment using the synchronization labels
Togood and Tobad. At both locations, the truck either speeds up to its maximum or
slows down to its minimum speed. After certain time passes, the control goes to loca-
tion Check, which assure that the truck reaches to the required destination point. In such
a case, a truck arrives either before deadline or after deadline. In both cases, the truck
has to inform the cargo wither with failure or with done, when it arrives after or before
deadline respectively.
Environment Automaton. Figure 2 models an environment that generates disturbance
during transportation process. This disturbance could be due to traffics, or a change in
weather. The Environment automaton is augmented with the variable envtime that
calculates the elapsed time at both location GoodConditon and BadCondition. The be-
havior of the environment automaton mutually oscillates between these two locations.
The control waits for gtime units at the location GoodCondition, while it waits for
btime time units at BadCondition location. Both gtime and btime represent the
time that environment takes at both locations.
Cargo Automaton. The automaton cargo is shown in Fig.3. The control of the cargo
begins at location Start. Then, it requests proposals from the participating trucks and the
control goes to location Wait-proposals. At this location, the cargo reports the received
messages that are coming from the different trucks (the messages are represented ei-
ther by Refuse
i
or Propose
i
synchronization labels and i={1,2}) . After all trucks
send their desired proposals, the control goes to location Evaluate-propos. From this
location, the control may go to one of the location Terminate, SelectAgent, or Bid. The
choice among these locations is depending on how many trucks propose to perform the
transportation. For example, if no truck proposes a proposal, the control goes to location
Terminate that means there is no truck agreed to perform the transportation. If there is
only one truck proposes a proposal, the control goes to location Bid. While, if more than
trucks propose proposal, the control goes to location SelectAgent. At this latter location,
the cargo selects a truck that provides a minimum price, and then the control goes to
location Bid. At location Bid, the cargo informs a selected truck with acceptance of the
proposal. In addition, the cargo will exclude the remaining truck using synchronization
label Reject-proposal . After that, the control goes to location Wait-arrived and
the cargo at this location waits for an incoming report from a truck that is responsi-
ble for the transportation process. Whenever the cargo receives Failuremessage, the
control goes to location Unsafe then goes to location Terminate.
146
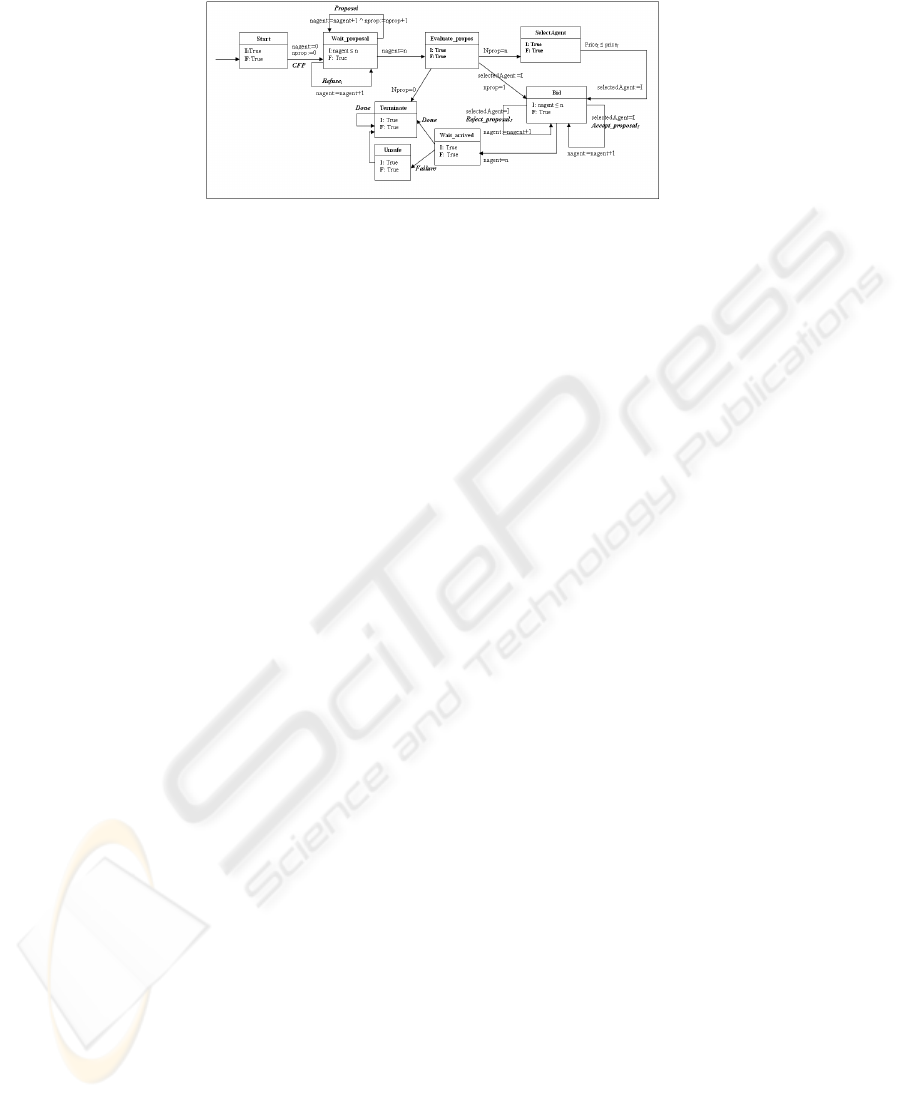
Fig.3. Cargo Automaton.
3.3 Entire Automaton
The previous multi-agent scenario typically consists of several agents that operate con-
currently and communicate with each other. We described each agent as a hybrid au-
tomaton component. Component automata coordinate through shared data variables and
synchronization labels. Nevertheless, the hybrid automaton that models the entire sys-
tem should be constructed to analyze behaviors of the modeled system. However, when
numbersof automata and numbers of states in each automata increase, it will be difficult
to understand the behavior of the entire system. This is because the entire automaton is
constructed from a product operation of the all participant automata. Fortunately, there
are model-checking tools that automatically construct the entire automaton and make
it accessible for formal verification (as we will see in the next section). Therefore, this
gives us the ability to concentrate on each automaton separately, and then input these
automata in a proper format to a model-checking tool, which in turn constructs the
entire automaton and performs some verification experiments.
4 Model Checking
Generally, a formal verification is a process in which mathematical techniques are used
to guarantee the correctness of a dosing with respect some behavior. A formal model of
a system allows its verification before it is built in order to determine design problem, or
it can be used to improve an existing one. Currently,the most successful approach to the
verification of formal models against formally expresses requirements is that of model
checking [2]. Generally, Model checking techniques allow verifying formally and auto-
matically if some properties of a system are satisfied in all possible system evolutions.
The process of model checking includes modeling, specification, and verification. In
modeling, a design is converted to a formalism accepted by a model checker (in our
case study we use hybrid automata). The specification process asserts the properties, de-
scribed in temporal logic, that the model has to satisfy. The verification process asserts
that the model meets the specification. Ideally, the verification using model checking is
completely automatic.
There are several existing model checker tools that are used to verify the properties
of the hybrid automata. Among of them are Hytech [8], and PHAVER [4]. We imple-
ment our model using Hytech. Hytech takes a textual representation of hybrid automata
as input and performs reachability analysis by exploring the entire state space of the
147

system. For more details about Hytech syntax, see [6]. Hytech computes the reacha-
bility of the entire state space by computing the set all states reachable from the initial
state, and then perform checking for needed properties using the resulting set. More-
over, Hytech provides a way that aids in design and debugging a system. For example,
if a system description contains design parameters, whose values are not specified, then
Hytech computes the necessary and sufficient constraints on the parameter values that
guarantee correctness. In addition, if a system fails to satisfy a correctness requirement,
then Hytech generates an error trajectory, which contains a time stamped sequence of
events that leads to a violation of the requirement.
In the rest of this section, we present some model checking experiments on our sce-
nario. We have proved various properties, depending on different values of the involved
variables in our model. Here, we will spot on some of them.
DEADLOCK OCCURRENCE: One system property, that is of general interest, is
the absence of deadlocks in the modeled system. This means that there is no con-
figuration that prevents one of the component automata from reaching its final loca-
tion(in our model, location Terminate in both cargo and truck is the final loca-
tion). Using Hytech, we showed that our model is indeed free of deadlocks by asking
if the formula f: location[Truck1]=terminate & location[Truck2]=terminate & loca-
tion[Cargo]=terminate is reached.
IS THERE A TRUCK THAT CAN PERFORM THE TRANSPORTATION? In our
scenario, there are two trucks involved in the process of transportation. We ensure that
only one truck will be responsible for performing the transportation by checking the
reachability of the formula f: location [Cargo] =selectAgent is reached. Moreover, this
truck always provides the minimum price.
DEADLINES: One of the most importance topic in the logistics domain is the ques-
tion whether a deadline can be met or not. Clearly ,the question if a truck will arrive
before or after a given deadline depends on a number of factors like the environmental
conditions during the transport, the transport distance ,and of course the deadline itself.
Using Hytech we did some experiments to answer this question for various values of
the deadline,as well as,the times gtime and btime of the environment. The speed of
the trucks in our experiments lays between 60 and 90, and the total distance that the
trucks had to travel, was 1100 and 1150. With btime=0 and gtime=5 several values
for the deadline were investigated. It turned out that the truck could always reach its
destination on time if the deadline was 17 time units, while a deadline of 12 time units
was impossible to meet. In order to determine the closest deadline for which the truck
was guaranteed to be on the due time,we use parametric analysis provided by Hytech.
This yielded 15.55 time units as the closest deadline that could always be met.
Similarly, some experiments were done to investigate the influence of the environ-
ment during the transport. For a given deadline=17and btime=5. Hytech’s analy-
sis has shown, that gtime = 0.888 time units is enough to ensure that the truck will
always arrive on time. If, on the other hand, gtime=2, then deadline=17can only
be met if btime <= 14.33. It is easy to see that the knowledge of boundaries and
dependencies between certain values as we presented above will help both the transport
agent and the customer to negotiate a contract that suits both parties.
148

5 Conclusions
Currently, most of multi-agent systems modeling languages are not able to verify some
properties of the modeled system. Therefore, we demonstrated, in this paper, how to
model a multi-agent system using the formalism of hybrid automata. This is because
hybrid automata are equipped with formal semantics that make them accessible to for-
mal validation of modeled behaviors using model-checking techniques. The context in
which we modeled our multi-agent system is taken from logistics process. This scenario
is mainly depending on FIPA contract net protocol. However, FIPA protocols are not
able to verify the properties of modeled multi-agent systems. Therefore, we modeled the
multi-agent system scenario using hybrid automata and with the help of HyTech model
checker; we verified certain properties of this scenario.Reachability analysis, which is
provided by model checking, helps us for finding out the possible paths, which could
help in the pre-computation of multi-agent system implementations. This point will be
subject of future work. Further, we intend to integrate a knowledge base with hybrid
automaton to reasoning about the dynamic behaviors of Multiagent system specially in
the logistic domain.
References
1. Bauer, B., Muller, J., and J. Odell.: Agent UML, a formalism for specifying multiagent soft-
ware systems, in Agent-Oriented Software Engineering, Ciancarini, P. and Wooldridge, M.,
Editors. LNCS, Vol. 1957, Vol., 2001: Springer, pp. 91-103
2. Clark, M., Grumberg, O., and Peled, D.: Model Checking. MIT Press. 2000
3. FIPA: FIPA contract net interaction protocol specification. Technical report, FIPA
(2002).Available from: http://www.fipa.org/specs/fipa00029/SC00029H.pdf
4. Frehse, G.: PHAVer:Alogrithmic verification for hybrid systems past Hytech. In Morari, M.,
Thiele, L. editors, Hybrid system: computation and control, 8th international workshop, pro-
ceedings, LNCS 3414, pages 258-273. Springer, 2005
5. Gehrke, J.D.,Behrens, C.,Jedermann, R., Morales-Kluge, E.: The intelligent Container-
Toward Autonomous Logistic Processes. In KI 2006 Demo Presentations, pp. 15?18, Jun 2006
6. Henzinger, T., Pei-Hsin, H., and Wong-Toi, H.: A user guide to HyTech. Proceedings of the
First International Conference on Tools and Algorithms for the Construction and Analysis of
Systems (TACAS), Lecture Notes in Computer Science 1019, Springer, 1995, pp. 41-71
7. Henzinger, T.: The theory of hybrid automata. In Proceedings of the 11th Annual Symposium
on Logic in Computer Science, pages 278-292. IEEE Computer Society Press, 1996
8. Henzinger, T., Pei-Hsin, H., and Wong-Toi, H.: HyTech: A Model Checker for Hybrid Sys-
tems. Software Tools for Technology Transfer 1:110-122, 1997
9. Russell, S., Norvig, P.: Artificial Intelligence: A Modern Approach. Prentice Hall, Upper Sad-
dle River, NJ, 2nd edition, 2003
10. Scholz-Reiter, B., Windt, K, and Freitag. M.: Autonomous logistic processes - New demands
and first approaches. In Proceedings of the 37th CIRP- International Seminar on Manufactur-
ing Systems, pp. 357?362, 2004
11. Wood, M., DeLoach, S.: An overview of the multiagent systems engineering methodology,
in Agent-Oriented Software Engineering, Ciancarini, P., Wooldridge, M., Editors. LNCS, Vol.
1957, 2001: Springer, pp. 207-221
12. Wooldridge, M., Jennings, N.R., and Kinny, D.: The Gaia methodology for agent-oriented
analysis and design. Autonomous Agents and Multi-Agent Systems, 2000
149
