
Key Establishment Algorithms for Some Deterministic
Key Predistribution Schemes
Sushmita Ruj and Bimal Roy
Applied Statistics Unit, Indian Statistical Institute
203 B T Road, Kolkata 700 108, India
Abstract. Key establishment is a major problem in sensor networks because of
resource constraints. Several key predistribution schemes have been discussed in
literature. Though the key predistribution algorithms have been described very
well in these papers, no key establishment algorithm has been presented in some
of them. Without efficient key establishment algorithm the key predistribution
schemes are incomplete. We present efficient shared-key discovery algorithms
for some known deterministic key predistribution schemes. Our algorithms run in
O (1) and O(
3
√
N) time and the communication overhead is at most O(log
√
N)
bits, where N is the size of the network. The efficient key establishment schemes
make deterministic key predistribution an attractive option over randomized sche-
mes.
1 Introduction
Distributed Sensor Networks (DSN) consist of sensor nodes which are resource con-
strained. Sensor networks have wide application in military as well as civilian purposes.
To ensure secure communication, any two sensor nodes should communicate in an en-
crypted manner using a common secret key.
The keys are either predistributed in the sensor nodes or online key exchange pro-
tocols can be used. Though public key cryptosystems using RSA and ECC have been
used in low end devices [1], they are not efficient where several hundred thousand nodes
with very limited resources are required. In key predistribution keys are placed in sen-
sor nodes prior to deployment. Any two nodes can communicate with each other if they
have some common key. Communication is carried out by encrypting messages using
the common key. Key establishment is carried out in the following way. First two nodes
find out if they have any common key and the identifier or the value of this common
key. This step is called shared key discovery. If two nodes do not share a common key
then a path key needs to be found. Path key establishment is discussed in Section 4.
The efficiency of key establishment algorithms depends on two factors.
1. The communication overhead - the amount of information that needs to be broad-
casted to enable other nodes to find the common keys.
2. Efficient shared key discovery algorithms - algorithms which are efficient in terms
of computation and storage.
Ruj S. and Roy B. (2008).
Key Establishment Algorithms for Some Deterministic Key Predistribution Schemes.
In Proceedings of the 6th International Workshop on Security in Information Systems, pages 68-77
DOI: 10.5220/0001729900680077
Copyright
c
SciTePress

Key predistribution techniques can be randomized, deterministic or hybrid. In ran-
domized technique of key predistribution by Eschenauer and Gligor [2] and Chan Per-
rig and Song [3], keys are drawn randomly from a key pool and placed in each sensor
node. Suppose each sensor contains k keys. In some schemes such as [2, 3], sensor
nodes broadcast the entire list of key identifiers. On receiving a list of identifiers a sen-
sor nodes compares it with its own identifier list to find a common identifier or a key
is computed from the common identifiers. All encryption and decryption is done using
this common key. For a key chains consisting of k keys O(k log v), bits needs to be
sent, where v = number of keys in the key pool. The identifiers may be sorted which
requires O(k log k) time. Then to find a common key identifier it takes O(k) time. This
fact was discussed by Lee and Stinson in [4, Section 2.1.2]. Another way is to use
Merkle puzzles as done by Eschenauer and Gligor in [2] and Chan, Perrig and Song
in [3]. Then to find a common shared key between two nodes, each node has to broad-
cast a list {α, E
k
i
(α), i = 1, 2, ··· , k}, where α is a challenge. The decryption of E
k
i
with proper key by the other node would reveal the challenge α and establish a shared
key with the broadcasting node. The communication overhead for the schemes [2, 3]
will be O(k log v), where v is the number of keys in the key pool. The calculation of
E
k
i
(α), i = 1, 2, ··· , k encryption will require O(k) time. However this is not a very
efficient way, since communication and computation complexity increases.
Deterministic key predistribution has the advantage that keys are placed in sensor
nodes in a predetermined manner. This helps us to device efficient algorithms for estab-
lishing the common keys between sensor nodes. Deterministic key predistribution using
combinatorial designs have been studied in [5–9]. Hybrid designs combine the above
two approaches and have been studied in [5, 10]. Though key predistribution algorithms
have been discussed in details [5, 8, 9], key establishment algorithms have not been
given in any of them. Without efficient key establishment algorithms the predistribution
schemes are incomplete. In ISPA ’07 Ruj and Roy proposed key predistribution scheme
using PBIBD (Partially balanced incomplete block designs) and in Inscrypt ’07 Dong,
Pei and Wang proposed a key predistribution scheme using 3 − designs. In both these
two schemes it was assumed that communication was carried using common shared
keys. However no algorithm for key establishment was given in both these papers. In
this paper we present efficient shared-key discovery algorithms for the key predistribu-
tion schemes given by Roy and Ruj [8] and Dong, Pei, Wang [9]. The algorithms run in
O(1) and O(
3
√
N) respectively. This makes them highly suitable for sensor networks.
The communication overhead is also very less, at most O(log
√
N) bits, where N is
the size of the network. Hence our schemes are better than those given in [2, 3]. The
design of these algorithms will motivate us towards designing deterministic predistri-
bution schemes.
The rest of the paper is organized as follows. In Section 2 and 3 we present key
establishment strategies for the key predistribution schemes given by Dong, Pei and
Wang in [9] and Ruj and Roy in [8]. Path key establishment has been represented in 4.
We conclude with some open problems in Section 5.
69

2 Shared-key Discovery for Key Predistribution Scheme given by
Dong, Pei and Wang [9]
The key predistribution scheme proposed by Dong et al. in [9] makes use of 3−designs.
In particular they use inversive planes to assign keys in the sensor nodes. We present
an algorithm to find a common key between two given nodes or report failure if no
common key is present. For completeness we present the key predistribution algorithm
using 3-designs. A detailed discussion on 3−designs can be found in [11, Section 9.2.1].
Let q be a prime. We use an irreducible polynomial f (x) of order 2 to construct a
field F
q
2
= Z
q
/(f(x)). Let f(x) = x
2
+ f
0
1
x + f
0
0
.
Let the field elements be f
0
= 0, f
1
= 1, f
2
, ···, f
q
2
−1
. We choose a, b, c, d ∈ F
q
2
,
such that ad − bc 6= 0. Let ∞ /∈ F
q
. We define a function
π
a b
c d
(x) =
ax+b
cx+d
if x ∈ F
q
and cx + d 6= 0
∞ if x ∈ F
q
, cx + d = 0 and ax + b 6= 0
a
c
if x = ∞ and c 6= 0
∞ if x = ∞, c = 0 and a 6= 0
Let P GL(2, q
2
) to consist of all distinct permutations π
a b
c d
, where a, b, c, d ∈
F
q
2
, such that ad − bc 6= 0. It can be proved as in [11, Lemma 9.25] that there are
q
6
−q
2
such permutations. We create blocks in the following way. For each permutation
π
i
, (i = 0, 1, 2, ··· , q
6
−q
2
−1) block B
π
i
consists elements π
i
(j), j = 0, 1, ··· , q −
1, ∞. So each block consists of q + 1 elements. The resulting design gives rise to a
3 − (q
2
+ q + 1, q + 1, 1) design.
We consider the distinct blocks and map the blocks to the nodes and preload each
node with the keys contained in that particular block. Since the number of distinct
blocks is q
3
+ q, the number of nodes supported by the network is q
3
+ q. Let the
key chain belonging to node i be denoted by {k
(i)
t
: 0 ≤ t ≤ q}. Any two nodes
can share at most two keys. Next we describe an algorithm to find the common keys
between any two nodes if one exists, or report failure if one doesn’t exists.
2.1 Algorithm to find Common Key
Let node i want to communicate with node j. The node j broadcasts corresponding
values of a, b, c, d. Denote these values by a
j
, b
j
, c
j
, d
j
. We give below the algorithm
to find the common key that i shares with j. When j wants to calculate the common key
that it shares with i, it runs the same algorithm and finds x
j
and calculates the common
key as ck =
a
j
x
j
+b
j
c
j
x
j
+d
j
. (See step 25). All calculations are done modulo q.
70
Algorithm 1. Shared key discovery for the scheme of Dong et al. [9].
Require a
i
, b
i
, c
i
, d
i
, a
j
, b
j
, c
j
, d
j
1 if c
i
= 0 and c
j
= 0
2 ck = ∞
3 else if a
i
/c
i
= a
j
/c
j
6= 0
4 ck = a
i
/c
i
5 else
6 tag = 0
7 for s = 0 to q
8 if k
(i)
s
= ∞
9 tag = 1
10 endif
11 endfor
12 if tag = 1
13 for s = 0 to q
14 if c
j
s + d
j
= 0
15 ck = ∞
16 else
17 Print : No solution exists
18 endif
19 endfor
20 else
21 Solve the equation
a
i
x
i
+b
i
c
i
x
i
+d
i
=
a
j
x
j
+b
j
c
j
x
j
+d
j
for x
i
.
22 if No solution exists then
23 Print : No solution exists
24 else
25 ck =
a
i
x
i
+b
i
c
i
x
i
+d
i
26 endif
27 endif
28 endif
Correctness of Algorithm 1. Suppose c
i
= 0 and c
j
= 0, then π
i
(∞) = π
j
(∞) = ∞,
hence ck = ∞ and Step 1-2 holds. If π
i
(∞) = a
i
/c
i
, if a
i
/c
i
6= 0. So if a
i
/c
i
=
a
j
/c
j
6= 0, then π
i
(∞) = π
j
(∞) = a
i
/c
i
and Step 3-4 holds. If one of the keys in
node i is ∞, and c
j
x
j
+ d
j
= 0, for some x
j
∈ F
q
S
{∞}, then ∞ is a common key
between the nodes i and j. The only condition that remains if that when x
i
, x
j
6= ∞
and c
i
x
i
+ d
i
6= ∞ and c
j
x
j
+ d
j
6= ∞. In such a case we try to find if there exists x
i
and x
j
, such that
a
i
x
i
+b
i
c
i
x
i
+d
i
=
a
j
x
j
+b
j
c
j
x
j
+d
j
. Hence if a solution to this equation exists, then
the common key will be
a
i
x
i
+b
i
c
i
x
i
+d
i
. By the design we know that any two nodes will share
maximum of two keys. We now show that we can find all the values of x
i
if they exist,
or report failure if no keys are common.
We know that a, b, c d are all one degree polynomial with coefficients in F
q
. Let
a
i
= a
i1
x + a
i0
, b
i
= b
i1
x + b
i0
, c
i
= c
i1
x + c
i0
, d
i
= d
i1
x + d
i0
,
a
j
= a
j1
x + a
j0
, b
j
= b
j1
x + b
j0
, c
j
= c
j1
x + c
j0
, d
j
= d
j1
x + d
j0
,
We solve for x
i
in the following equation. Note that all calculations are done modulo
q.
71

a
i
x
i
+b
i
c
i
x
i
+d
i
=
a
j
x
j
+b
j
c
j
x
j
+d
j
⇒ (a
i
x
i
+ b
i
)(c
j
x
j
+ d
j
) = (c
i
x
i
+ d
i
)(a
j
x
j
+ b
j
)
⇒ {(a
i1
x + a
i0
)x
i
+ (b
i1
x + b
i0
)}{(c
j1
x + c
j0
)x
j
+ (d
j1
x + d
j0
)}
= {(c
i1
x + c
i0
)x
i
+ (d
i1
x + d
i0
)}{(a
j1
x + a
j0
)x
j
+ (b
j1
x + b
j0
)}
⇒ {(a
i1
x
i
+ b
i1
)x + (a
i0
x
i
+ b
i0
)}{(c
j1
x
j
+ d
j1
)x + (c
j0
x
j
+ d
j0
)}
= {(c
i1
x
i
+ d
i1
)x + (c
i0
x
i
+ d
i0
)}{(a
j1
x
j
+ b
j1
)x + (a
j0
x
j
+ b
j0
)}
⇒ x{(a
i1
x
i
+ b
i1
)(c
j0
x
j
+ d
j0
) + (a
i0
x
i
+ b
i0
)(c
j1
x
j
+ d
j1
) +
(q − f
0
1
)(a
i1
x
i
+ b
i1
)(c
j1
x
j
+ d
j1
)} +
(a
i0
x
i
+ b
i0
)(c
j0
x
j
+ d
j0
) + (q − f
0
0
)(a
i1
x
i
+ b
i1
)(c
j1
x
j
+ d
j1
)}
= x{(a
j1
x
j
+ b
j1
)(c
i0
x
i
+ d
i0
) + (a
j0
x
j
+ b
j0
)(c
i1
x
i
+ d
i1
) +
(q − f
0
1
)(a
j1
x
j
+ b
j1
)(c
i1
x
i
+ d
i1
)} +
(a
j0
x
j
+ b
j0
)(c
i0
x
i
+ d
i0
) + (q − f
0
0
)(a
j1
x
j
+ b
j1
)(c
i1
x
i
+ d
i1
)}
Equating the coefficients of x and the constant term we get two equations
P
1
x
i
x
j
+ Q
1
x
i
+ R
1
x
j
+ S
1
= 0 (1a)
and
P
2
x
i
x
j
+ Q
2
x
i
+ R
2
x
j
+ S
2
= 0 (1b)
where,
P
1
= a
i1
c
j0
+ a
i0
c
j1
+ (q − f
0
1
)a
i1
c
j1
− (a
j1
c
i0
+ a
j0
c
i1
+ (q − f
0
1
)a
j1
c
i1
),
P
2
= a
i0
c
j0
+ (q − f
0
0
)a
i1
c
j1
− (a
j0
c
i0
+ (q − f
0
0
)a
j1
c
i1
),
Q
1
= a
i1
d
j0
+ a
i0
d
j1
+ (q − f
1
)a
i1
d
j1
− (b
j1
c
i0
+ b
j0
c
i1
+ (q − f
0
1
)b
j1
c
i1
),
Q
2
= a
i0
d
j0
+ (q − f
0
0
)a
i1
d
j1
− (b
j0
c
i0
+ (q − f
0
0
)b
j1
c
i1
),
R
1
= b
i1
c
j0
+ b
i0
c
j1
+ (q − f
0
1
)b
i1
c
j1
− (a
j1
d
i0
+ a
j0
d
i1
+ (q − f
0
1
)a
j1
d
i1
),
R
2
= b
i0
c
j0
+ (q − f
0
0
)b
i1
c
j1
− (a
j0
d
i0
+ (q − f
0
0
)a
j1
d
i1
),
S
1
= b
i1
d
j0
+ b
i0
d
j1
+ (q − f
0
1
)b
i1
d
j1
− (b
j1
d
i0
+ b
j0
d
i1
+ (q − f
0
1
)b
j1
d
i1
),
S
2
= b
i0
d
j0
+ (q − f
0
0
)b
i1
d
j1
− (b
j0
d
i0
+ (q − f
0
0
)b
j1
d
i1
).
Eliminating the term x
i
x
j
, we get
(
Q
1
P
1
−
Q
2
P
2
)x
i
+ (
R
1
P
1
−
R
2
P
2
)x
j
=
S
2
P
2
−
S
1
P
1
x
j
= U + V x
i
(2)
where, U = (
S
2
P
2
−
S
1
P
1
)(
R
1
P
1
−
R
2
P
2
)
−1
and V = q − (
Q
1
P
1
−
Q
2
P
2
)(
R
1
P
1
−
R
2
P
2
)
−1
Substituting the value of x
j
in ( 1a) we get
P
1
(V x
i
+ U)x
i
+ Q
1
(V x
i
+ U) + R
1
(V x
i
+ U) + S
1
= 0
⇒ P
1
V x
2
i
+ x
i
(UP
1
+ V Q
1
+ V R
1
) + UP
1
+ UQ
1
+ UR
1
+ S
1
= 0
where
The above equation can have either one or two or no solutions which can be calcu-
lated easily. Hence, we obtain a maximum of two values for x
i
. Then the common key
72

will be
a
i
x
i
+b
i
c
i
x
i
+d
i
. Thus the algorithm gives all the common keys or reports failure if none
is present.
Time Complexity of Algorithm 1. Steps 7 to 10 are executed at most q times. All the
other steps require constant time. Since the number of nodes N is O(
3
√
N), the time
complexity is O(
3
√
N). Only the four values of a, b, c and d need to be broadcasted.
Hence the communication overhead is O(log q) bits, which is quite efficient compared
to algorithms proposed in [2, 3].
3 Shared-key Discovery for Ruj and Roy Schemes of Key
Predistribution [8]
Two key predistribution schemes have been discussed in [8]. Both the schemes make
use of Partially balanced incomplete block designs for key predistribution.
Ruj and Roy Scheme [8] I. The authors use a triangular association scheme to predis-
tribute the keys in the sensor network. The design can be found in [8, Section 3]. We
now give an algorithm to find at least one common key between two given nodes.
3.1 Algorithm to find Common Key
Let nodes P and Q want to communicate with each other. For this purpose we store
the location of the node in the array A. The nodes broadcast their position in the array
A. We need to calculate a simple function which will give the identity of one or more
common key between any two nodes. Given the position (x, y) of a node P the value
in the matrix at position (x, y) is given by
f(x, y) =
∗, for x = y
y − x, for x = 1, x < y
x − y, for y = 1, x > y
n + y − x − 1, for x = 2, x < y
n + x − y − 1, for y = 2, x > y
(x − 1)n − (x + 1)(x − 2)/2 + (y − x − 1), for x < y, x > 2
(y − 1)n − (y + 1)(y − 2)/2 + (x − y − 1). for x > y, y > 2
Given any node P it can find the ids of the keys in common with another node Q at
position (x
0
, y
0
) in the following way.
1. If x = x
0
, then a
f(x,t)
and a
f(y,y
0
)
are the common keys between P and Q for
t = 1, 2, ··· , n and t 6= x, y, y
0
.
2. If y = y
0
, then a
f(t,y)
and a
f(x,x
0
)
are the common keys between P and Q for
t = 1, 2, ··· , n and t 6= x, y, x
0
.
3. If x 6= x
0
and y 6= y
0
, then the keys a
f(x,x
0
)
, a
f(x,y
0
)
, a
f(y,x
0
)
and a
f(y,y
0
)
are com-
mon between P and Q.
Since there are more than one keys in common, the nodes can choose any of the com-
mon keys. Since f(x, y) can be calculated in constant time, key agreement can be done
in O(1) time. Also the memory overhead is O(log n) = O(log
√
N) bits, since only
the position of the node in the array is sent.
73

Ruj and Roy Scheme [8] II. The second scheme given in [8] is an extension of Scheme
I. Here a second array A
0
is used in conjunction to the array A given above. Array A
0
is given in [8, Section 5.1]. The first n(n − 1)/2 are loaded as given in the Scheme I.
For the next n(n − 1)/2 nodes, keys are chosen according to the pattern in array A
0
.
For the n(n − 1)/2 + ith node, the ids of the keys are the elements in the row and the
column in which i belongs. The element in the position (x, y) in the matrix A
0
is given
by f
0
(x, y) =
∗, for x = y
(x − y − 1)(2n − x + y)/2 + y, for x > y
(y − x − 1)(2n − y + x)/2 + x otherwise
3.2 Algorithm to find Common Key
Let the nodes i and j want to communicate with each other. Any node j broadcasts the
following information.
1. Array s from which j was derived. m[s] = 0 if j is derived from A and m[s] = 1
if j is derived from A
0
. This requires one bit.
2. Position (x
j
, y
j
) of j in the array from which it has been derived. This requires
O(log
√
N).
Given the above information node i can calculate the common keys using Algorithm 2.
3.3 Proof of Correctness and Time Complexity of Algorithm 2
If both the nodes i and j are derived from the same array, then we follow the algorithm
similar to that given in Section 4.1. We will consider the case when i and j are derived
from arrays A
0
and A respectively. The case where i and j are derived from arrays A
and A
0
respectively will follow similarly.
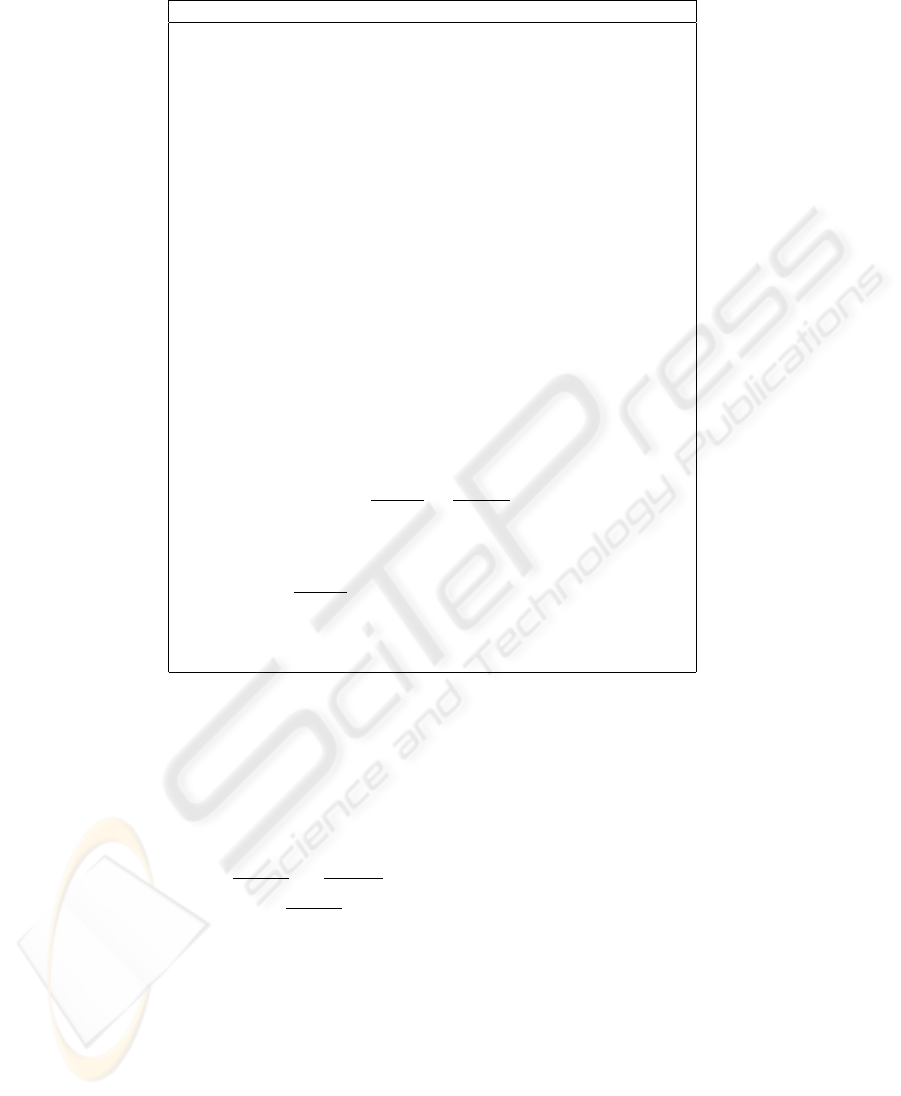
We consider the following example
Example. Suppose position of i = (5, 7) in array A
0
and that of j = (4, 6) in array A.
Ids of keys belonging to j are 3, 9, 14, 19, 21, 22 and 5, 11, 16, 23, 26, 27. These have
been marked in array A
0
as below. We mark four diagonal lines and two vertical lines
and two horizontal lines. We find all the crossed elements that lie in the 7th column.
These are the elements common between i and j which occur along the two diagonals.
These are 26 and 21. Similarly, all the crossed elements that lie in the 5th row are the
common elements between i and j. These are 19 and 5 in the above example. So the
common keys have identifiers 5, 19, 21 and 26.
74

Algorithm 2. Shared key Discovery for Scheme II.
1 if m[i] = m[j] = 0
2 if x
i
= x
j
3 Ids of the common keys are a
f(x
i
,t)
and a
f(y
i
,y
j
)
, for t = 1, 2, ··· , n
and t 6= x
i
, y
i
, y
j
4 else if y
i
= y
j
5 Ids of the common keys are a
f(t,y
i
)
and a
f(x
i
,x
j
)
, for t = 1, 2, ··· , n
and t 6= x
i
, y
i
, x
j
6 else
7 Ids of the common keys a
f(x
i
,x
j
)
, a
f(x
i
,y
j
)
, a
f(y
i
,x
j
)
and a
f(y
i
,y
j
)
.
8 endif
9 else if m[i] = m[j] = 1
10 if x
i
= x
j
11 Ids of the common keys are a
f
0
(x
i
,t)
and a
f
0
(y
i
,y
j
)
, for t = 1, 2, ··· , n
and t 6= x
i
, y
i
, y
j
.
12 else if y
i
= y
j
13 Ids of the common keys are a
f
0
(t,y
i
)
and a
f
0
(x
i
,x
j
)
, for t = 1, 2, ··· , n
and t 6= x
i
, y
i
, x
j
.
14 else
15 Ids of the common keys a
f
0
(x
i
,x
j
)
, a
f
0
(x
i
,y
j
)
, a
f
0
(y
i
,x
j
)
and a
f
0
(y
i
,y
j
)
.
16 end if
17 else if m[i] = 1 and m[j] = 0
18 Ids of the common keys as calculated by i will be a
f
0
(a,b)
where
1. (a, b) = (y
i
− x
j
, y
i
), (y
i
− y
j
, y
i
), (y
i
+ x
j
, y
i
), (y
i
+ y
j
, y
i
), (x
i
, x
i
− x
j
),
(x
i
, x
i
− y
j
), (x
i
, x
i
+ x
j
), (x
i
, x
i
+ y
j
), such that 0 < a, b ≤ n and a 6= b.
2. (a, b) = (x
i
, x
j
), (x
i
, y
j
) if a < b, x
i
6= x
j
3. (a, b) = (x
j
, y
i
), (y
i
, y
i
) if a > b, y
i
6= y
i
4. (x
i
, 1), (x
i
, 2), ··· , (x
i
, x
i−1
) if x
j
= x
i
.
5. (1, y
i
), (2, y
i
), ··· , (y
i−1
, y
i
) if y
j
= y
i
.
19 else
20 Ids of the common keys will be calculated as above except that the f
(a,b)
will be calculated instead of f
0
(a,b)
.
21 endif
Proceeding as in the example above there will be at most four diagonal lines and two
vertical lines and two horizontal lines. The position of the elements along the marked
diagonals that lie on the same column as i will be given by, (a, b) = (y
i
−x
j
, y
i
), (y
i
−
y
j
, y
i
), (y
i
+ x
j
, y
i
), (y
i
+ y
j
, y
i
) such that 0 < a, b ≤ n and a 6= b.
Similarly, all the positions of the elements along the marked diagonals that lie on the
same row as i and is given by (a, b) = (x
i
, x
i
−x
j
), (x
i
, x
i
−y
j
), (x
i
, x
i
+x
j
), (x
i
, x
i
+
y
j
), such that 0 < a, b ≤ n and a 6= b.
If both i and j belong to the same row (ie, x
i
= x
j
), then the position of the common
elements will be (a, b) = (x
i
, 1), (x
i
, 2), ··· , (x
i
, x
i−1
). These elements lie on one of
the marked rows. If both i and j belong to the same column (ie, y
i
= y
j
), then the
position of the common elements will be (a, b) = (1, y
i
), (2, y
i
), ··· , (y
i−1
, y
i
). These
elements lie on one of the marked columns. If i and j do not belong to the same row
75

*
*
1
*
*
*
*
*
2 3 4 5 6 7
9 10 11 12 13
14
15 16 17 18
19 20 21 22
23 24 25
26 27
28
1
2
3
4
5
6
7
8
9
10
11
12
13
*
14
15
16
17
18
19
20
21
22
23
24
25
26
27 28
8
(a) array 1
*
*
1 8 14
2 9 15 20
19 23 26 28
24 27
* 3 10 16 21 25
* 4 11 17 22
* 5 12 18
* 6 13
* 7
1
8
19
23
26
28
2
9
15
20
24
27
3
10
16
21
4
5
6
7 *
11
17 12
1315 1822
14
(b) array 2
Fig. 1. Array 1 and array 2.
or column, then the positions will be given by (a, b) = (x
i
, x
j
), (x
i
, y
j
) if a < b and
(a, b) = (x
j
, y
i
), (y
i
, y
i
) if a > b. So the ids of the common keys are given by f
0
(a,b)
. To
communicate, the nodes can choose any of the common keys. All the steps take O(1)
to be done. Hence the overall time complexity is O(1).
Each node broadcasts the array to which it belongs (this requires just one bit) and its
position in the array from which it is derived. Since the order of each array is O(
√
N)
(where N is the number of nodes), O(log
√
N) bits have to be broadcasted.
4 Path Key Establishment
Where shared key exists between nodes, a secure channel is created and all communica-
tions between the nodes are performed using the common key. However there may exist
situations where nodes may not share common keys (as in the scheme of [9] which uses
t − designs) or when common shared keys are exposed because of node compromise.
In such cases a path needs to be established between the nodes. Suppose u and v having
no common key need to communicate with each other. u establishes communication
with some node n
1
through some common key which further establishes communica-
tion with n
2
and so onwards. Let u, n
1
, n
2
, ··· , n
l
, w be the path between u and v. Let
u share a common key k
1
with n
1
. Similarly, let n
1
share a common key k
2
with n
2
,
and n
l−1
share a common key k
l
with n
l
and n
l
share a common key k
l+1
with w. u
generates a random key K, encrypts with k
1
and sends it to n
1
. n
1
decrypts K using
k
1
and encrypts it using k
2
and sends it to n
2
and the process continues. Ultimately
K reaches v using k
l+1
. So v can decrypt using k
l+1
and obtain K. K is the path key
and communication between u and v is done using K. This approach has been taken in
[12]. The path is found in a breadth first manner.
5 Conclusions
Various deterministic key predistribution have been studied in literature. However effi-
cient key establishment has not been discussed for many key predistribution schemes.
We present key shared-key discovery algorithms for the key predistribution schemes
76

given by Ruj and Roy in [8] and by Dong, Pei and Wang in [9] , which had not been
presented in these papers. The algorithms run in O(1) and O(sqrt[3]N) respectively.
Also communication requires at most O(log
√
N) bits, where N is the size of the net-
work. Randomized key predistribution algorithms lack efficient key management strate-
gies because there is no underlying pattern. The efficient key establishment strategies of
deterministic schemes as given in this paper motivates us to use deterministic schemes
for key predistribution. We are working towards devising algorithms for shared key dis-
covery for other known key predistribution schemes. One interesting problem will be to
design efficient key establishment schemes for randomized key predistribution schemes.
References
1. Gura, N., Patel, A., Wander, A., Eberle, H., Shantz, S.C.: Comparing elliptic curve cryp-
tography and rsa on 8-bit cpus. In Joye, M., Quisquater, J.J., eds.: CHES. Volume 3156 of
Lecture Notes in Computer Science., Springer (2004) 119–132
2. Eschenauer, L., Gligor, V.D.: A key-management scheme for distributed sensor networks. In
Atluri, V., ed.: ACM Conference on Computer and Communications Security, ACM (2002)
41–47
3. Chan, H., Perrig, A., Song, D.X.: Random key predistribution schemes for sensor networks.
In: IEEE Symposium on Security and Privacy, IEEE Computer Society (2003) 197–
4. Lee, J., Stinson, D.R.: On the construction of practical key predistribution schemes for
distributed sensor networks using combinatorial designs. ACM Trans. Inf. Syst. Secur. 11
(2008)
5. C¸ amtepe, S.A., Yener, B.: Combinatorial design of key distribution mechanisms for wireless
sensor networks. In Samarati, P., Ryan, P.Y.A., Gollmann, D., Molva, R., eds.: ESORICS.
Volume 3193 of Lecture Notes in Computer Science., Springer (2004) 293–308
6. Lee, J., Stinson, D.R.: Deterministic key predistribution schemes for distributed sensor net-
works. In Handschuh, H., Hasan, M.A., eds.: Selected Areas in Cryptography. Volume 3357
of Lecture Notes in Computer Science., Springer (2004) 294–307
7. Lee, J., Stinson, D.R.: A combinatorial approach to key predistribution for distributed sensor
networks. In: IEEE Wireless Communications and Networking Conference, WCNC 2005,
New Orleans, LA, USA. (2005)
8. Ruj, S., Roy, B.K.: Key predistribution using partially balanced designs in wireless sensor
networks. In Stojmenovic, I., Thulasiram, R.K., Yang, L.T., Jia, W., Guo, M., de Mello, R.F.,
eds.: ISPA. Volume 4742 of Lecture Notes in Computer Science., Springer (2007) 431–445
9. Dong, J., Pei, D., Wang, X.: A key predistribution scheme using 3-designs. In: INSCRYPT.
(2007)
10. Chakrabarti, D., Maitra, S., Roy, B.K.: A key pre-distribution scheme for wireless sensor
networks: Merging blocks in combinatorial design. In Zhou, J., Lopez, J., Deng, R.H., Bao,
F., eds.: ISC. Volume 3650 of Lecture Notes in Computer Science., Springer (2005) 89–103
11. Stinson, D.: Combinatorial Designs: Constructions and Analysis. Springer-Verlag, New
York (1987)
12. Du, W., Deng, J., Han, Y.S., Varshney, P.K.: A key predistribution scheme for sensor net-
works using deployment knowledge. IEEE Trans. Dependable Sec. Comput. 3 (2006) 62–77
77
