New Attack Strategy for the Shrinking Generator
Pino Caballero-Gil
1
, Amparo F´uster-Sabater
2
and M. Eugenia Pazo-Robles
3
1
Faculty of Mathematics, University of La Laguna, 38271 Tenerife, Spain
2
Institute of Applied Physics, C.S.I.C., Serrano 144, 28006 Madrid, Spain
3
Argentine Business University, Lima 717, Buenos Aires, Argentina
Abstract. This work shows that the cryptanalysis of the shrinking generator re-
quires fewer intercepted bits than what indicated by the linear complexity. Indeed,
whereas the linear complexity of shrunken sequences is between A· 2
(S−2)
and
A· 2
(S−1)
, we claim that the initial states of both component registers are easily
computed with fewer than A · S shrunken bits. Such a result is proven thanks to
the definition of shrunken sequences as interleaved sequences. Consequently, it is
conjectured that this statement can be extended to all interleaved sequences. Fur-
thermore, this paper confirms that certain bits of the interleaved sequences have a
greater strategic importance than others, which must be considered as a proof of
weakness of interleaved generators.
1 Introduction
Stream ciphers are considered nowadaysthe fastest encryption procedures. Consequent-
ly, they are implemented in many practical applications e.g. the algorithms A5 in GSM
communications [10], the encryption system E0 in Bluetooth specifications [2] or the
algorithm RC4 [15] used in Microsoft Word and Excel.
From a short secret key (known only by the two interested parties) and a public al-
gorithm (the sequence generator), a stream cipher procedure is based on the generation
of a long sequence of seemingly random bits. Such a sequence is called the keystream
sequence.
For the encryption the sender realizes the bit-wise (Exclusive-OR) XOR operation
among the bits of the original message or plaintext and the keystream sequence. The
result is the ciphertext to be sent. For the decryption, the receiver generates the same
keystream, realizes the same bit-wise XOR operation between the received ciphertext
and the keystream sequence and obtains again the original message.
Most keystream generators are based on Linear Feedback Shift Registers (LFSRs)
[8], which are linear structures characterized by their length (the number of memory
cells), their characteristic polynomial (the feedback function) and their initial states
(the seed or key of the cryptosystem). If the characteristic polynomial is a primitive
polynomial [14], then the LFSRs generate Pseudo- Noise sequences (PN-sequences)
with good characteristics of pseudorandomness.
For a survey on primitive LFSRs, PN-sequences, and shift equivalences the in-
terested reader is referred to [8]. In stream cipher procedures, the PN- sequences are
Caballero-Gil P., Fúster-Sabater A. and Pazo-Robles M. (2008).
New Attack Strategy for the Shrinking Generator.
In Proceedings of the 6th International Workshop on Security in Information Systems, pages 59-67
DOI: 10.5220/0001735200590067
Copyright
c
 SciTePress

combined by means of nonlinear functions in order to produce keystream sequences of
cryptographic application. Combinational generators, nonlinear filters, clock-controlled
generators,irregularly decimated generators ... are just some of the most popular nonlin-
ear sequence generators. All of them produce keystreams with high linear complexity,
long period and good statistical properties (see [6] and [3]).
Most cryptanalysis on stream ciphers are performed under a known plaintext hy-
pothesis, that is to say, it is assumed that the attacker has direct access to a portion
of the keystream sequence (the intercepted sequence). From the intercepted bits, the
attacker has to deduce the cryptosystem key. Once the key is known, as the sequence
generator is public, the whole keystream sequence can be reconstructed. The complex-
ity of this attack is always compared with that of the key exhaustive search. If the former
complexity is lesser, then the cryptosystem is said to be broken.
This work focuses on a particular kind of stream ciphers based on LFSRs: the class
of shrinking generators. They are made out of two LFSRs and an irregular decimation.
Shrinking generators have been thoroughly analyzed in several papers such as [17],
[13] and [4]. Nevertheless, we present a new and efficient cryptanalytic attack requiring
much lesser amount of intercepted bits than that of the previous attacks. The basic idea
of this cryptanalysis consists in defining the output sequence of a shrinking generator as
an interleaved sequence (see [9] and [12]). The characteristics of interleaved sequences
reveals weaknesses that lead to practical attacks. In addition, we conjecture that these
weaknesses can be extended to all interleaved sequence generators with application in
cryptography.
The paper is organized as follows: in section 2, the description and characteristics
of the shrinking generator is introduced. Interleaved configuration and related results
are developed in section 3. A cryptanalitic attack against the shrinking generator that
exploits the condition of interleaved sequence is presented in section 4, while the gen-
eralization of this technique to other cryptographic interleaved generators appears in
section 5. Finally, conclusions in section 6 end the paper.
2 The Shrinking Generator
The so-called Shrinking Generator (SG) is a nonlinear keystream generator composed
by two LFSRs [5] so that a control register SRS decimates the sequence produced by
the other register SRA. S and A denote respectively their corresponding lengths and
fulfil that (S,A) = 1 and S < A. P
S
(x) and P
A
(x) ∈ GF(2)[x] denote their corresponding
primitive characteristic polynomials.
The sequence {s
i
} produced by SRS controls the bits of the sequence {a
i
} produced
by SRA which are included in the output shrunken sequence {z
j
} according to the fol-
lowing rule: If s
i
= 1 then z
j
= a
i
, and if s
i
= 0, then a
i
is discarded.
As different pairs of SRA/SRS initial states can generate the same shrunken se-
quence, in the sequel we assume that the first term of the sequence {s
i
} equals 1, that is
s
0
= 1. According to [5], the period of the shrunken sequence is:
T = (2
A
− 1)2
(S−1)
, (1)
60

its linear complexity, notated LC, satisfies the following inequality:
A· 2
(S−2)
< LC ≤ A· 2
(S−1)
, (2)
and its characteristic polynomial is of the form:
P
ss
(x) = (P(x))
p
(3)
where P(x) is an A-degree primitive polynomial in GF(2)[x] and p is an integer in the
interval 2
(S−2)
< p ≤ 2
(S−1)
. Moreover,it can be proven [16] that the shrunken sequence
has also good distributionalstatistics. Therefore, this scheme has been traditionally used
as keystream sequence generator with application in secret-key cryptography.
3 Interleaved Configuration
The (2
A
−1)·2
(S−1)
bits of a period of any shrunken sequence {z
j
} can be arranged into
a(2
A
−1)×2
(S−1)
matrix that we will call interleavedconfiguration and will denote by
IC. In fact,
IC =








z
0
z
1
· z
2
S−1
−1
z
2
S−1
z
2
S−1
+1
· z
2·2
S−1
−1
z
2·2
S−1
z
2·2
S−1
+1
· z
3·2
S−1
−1
z
3·2
S−1
z
3·2
S−1
+1
· z
4·2
S−1
−1
··· ··· · ···
z
(2
A
−2)·2
S−1
z
(2
A
−2)·2
S−1
+1
· z
(2
A
−1)·2
S−1
−1








Now the following result allows one to identify each element of the matrix IC with
the corresponding term of the sequence {a
i
}.
Theorem 3.1. The interleaved configuration matrix IC can be written in terms of the
elements of the sequence {a
i
} such as follows:
IC =








a
o0
a
o1
···
a
2
S−1
+o0
a
2
S−1
+o1
···
a
2·2
S−1
+o0
a
2·2
S−1
+o1
···
a
3·2
S−1
+o0
a
3·2
S−1
+o1
···
··· ··· ···
a
(2
A
−2)·2
S−1
+o0
a
(2
A
−2)·2
S−1
+o1
···








where the additive sub-indices o j ( j = 0,1,··· ,2
S−1
− 1) depend on the bits of the
sequence {s
i
} in the following way: if s
i
= 1, then the corresponding sub-index oj
equals the sub-index i, o j = i. All the sub-indices are taken module 2
A
− 1, that is to
say, the period of the sequence {a
i
}.
Proof. Since the period of the PN-sequence {s
i
} is (2
S
− 1), the number of bits with
value 1 in a period is exactly 2
S−1
, and all the elements of any column of IC come from
the same term s
i
= 1 of the PN-sequence, the above expression for the matrix IC in
terms of the elements of {a
i
} is obtained. 
61

According to the assumption s
0
= 1, the sub-index o0= 0. Next, the followingresult
analyzes the characteristics of the columns of the matrix IC.
Theorem 3.2. The sequences {d
j
} = {a
k+oj
: k = 0,(2
S
− 1),2· (2
S
− 1),··· ,(2
A
− 2) ·
(2
S
− 1)}( j = 0,1, · · · ,2
((S−1)
− 1) corresponding to the columns of the matrix IC are
shifted versions of a unique PN-sequence whose characteristic polynomial is given by:
P
D
(x) = (x+ α
N
)(x+ 2N)(x+ α
2·N
)·· · (x+ α
2·(A−1)·N
)
where N is an integer defined as N = 2
0
+ 2
1
+ ··· + 2
(S−1)
and α ∈ GF(2
A
) a root of
the primitive polynomial P
A
(x).
Proof. Every sequence {d
j
} corresponding to the j-th column of IC is a regular
decimation of the PN-sequence {a
i
}. More precisely, such a sequence is obtained by
taking one out of (2
S
− 1) terms in {a
i
}. The primality between A and S guarantees the
primality between (2
A
− 1) and (2
S
− 1). Thus, the decimated sequence { d
j
} is also a
PN-sequence. In addition, as every {d
j
} has been obtained from {a
i
} with a decimation
ratio of value (2
S
− 1), then its characteristic polynomial P
D
(x) is the polynomial of
the cyclotomic coset (2
S
− 1) in the Galois Field GF(2
A
) generated by the roots of the
polynomial P
A
(x), see [4]. The starting point of each {d
j
} is given by the corresponding
sub-index oj. 
4 Cryptanalytic Attack
The cryptanalytic attack consists in the computation of the initial states of both registers
SRA and SRS. In fact, from some known bits of the shrunken sequence we have to
determine the first A bits (a
0
,a
1
,··· , a
A−1
) of the sequence {a
i
} as well as the first S
bits (s
0
,s
1
,··· , s
S−1
) of the sequence {s
i
}. This attack can be divided into two different
steps. In the first one, the computation of the initial state of SRA is carried out. In the
second step and based on the SRA initial state, we determine the corresponding initial
state of the register SRS.
4.1 SRA Initial State
Previously to the computation of the initial state, the following result is introduced.
Lemma 4.1. Given A bits of the shrunken sequence corresponding to A successive ele-
ments of any column of IC, the remaining bits of such a column can be determined.
Proof. Theorem 3.2 determines P
D
(x) the characteristic polynomial of the PN-sequence
corresponding to every column of IC. Thus, knowing A successive bits of any column
and its characteristic polynomial, the linear recurrence relationship allows one to com-
pute the remaining bits of such a column. 
Now the computation of the SRA initial state is described in the next result.
Theorem 4.2. Given A bits of the shrunken sequence corresponding to A successive
elements of the first column of IC, the bits of the initial state of the register SRA can be
determined.
62

Proof. Lemma 4.1 shows that the knowledge of A successive elements of the first
column of IC allows one to generate the remaining bits of such a column. On the other
hand, from Theorem 3.1 we know that the (n+ 1)-th element of the first column of IC
corresponds to a
n·(2
S
−1)
, that is to say, the (n · (2
S
− 1) + 1)-th term of the sequence
generated by the register SRA. Consequently, we first solve the following system of
modular equations in the unknowns n
i
n
i
· (2
S
− 1) ≡ i mod(2
A
− 1)(i = 0,1,··· , (A − 1)),
and then we compute successively the (n
i
+ 1)-th (i = 0, 1, · · · ,(A− 1)) elements of the
first column of IC in order to obtain a
0
,a
1
,··· , a
A
− 1, respectively. 
4.2 SRS Initial State
The computation of the SRS initial state is described in the next result.
Theorem 4.3. Given A· S bits of the shrunken sequence corresponding to the top-left
corner (A× S) sub-matrix of IC, the bits of the initial state of the register SRS can be
determined.
Proof. Firstly, from the knowledge of the (A× S) sub-matrix of IC,
SUB
IC
=








a
0
a
o1
···
a
2
S
−1
a
(2
S
−1)+01
···
a
2·2
S
−1
a
2·(2
S
−1)+01
···
a
3·2
S
−1
a
3·(2
S
−1)+01
···
··· ··· ···
a
(A−1)·2
S
−1
a
(A−1)·(2
S
−1)+01
···








and according to Lemma 4.1, we can deduce the remaining bits of those S columns.
Secondly, the relative shifts among columns may be computed from the comparison
between consecutive columns. Since the sequence in every column of IC is exactly the
same but starting at different points given by a
oj
, as soon as a relative shift is found
the sub-index oj may be easily computed. In addition, each sub-index oj indicates the
position of the (j + 1)-th 1 in the initial state of SRS while the intermediate bits are 0’s.
Thus, the above procedure can be repeated for j = 1,2,··· till we get oj ≥ (S− 1). In
this way, the initial state of the register SRS is thoroughly determined. 
4.3 Illustrative Example
Let us consider a shrinking generator characterized by:
(1) SRA with length A= 5, characteristic polynomial P
A
(x) = x
5
+ x
4
+ x
3
+ x
2
+ 1
and output sequence {a
i
} .
(2) SRS with length S= 4, characteristic polynomial P
S
(x) = x
4
+ x
3
+ 1 and output
sequence {s
i
}.
(3) The characteristic polynomial of the shrunken sequence is P
ss
(x) = P
D
(x)
p
=
(x
5
+ x
3
+ x
2
+ x+ 1)
8
.
Given 20 bits of the shrunken sequence corresponding to a (5× 4) sub-matrix of IC
63

SUB
IC
=






1 0 1 1
1 0 0 1
0 1 0 1
0 1 1 1
0 0 0 1






we can launch a cryptanalytic attack against the shrinking generator in order to obtain
the initial states of both LFSRs. Table 1 shows the calculations carried out for cryptan-
alyzing the above described generator. The most left column represents the indices n
i
numbered (0,··· , 2
A
− 2 = 30). Next column shows from Theorem 3.1 the position of
the terms (a
0
,a
1
,··· ,a
4
) of the sequence {a
i
} in the first column {d
o
} of the matrix IC.
The following columns of the Table 1 represent the matrix IC: in boldface the (5 × 4)
sub-matrix with the known bits, the remaining bits of {d
0
} are the bits computed to
determine the initial states of SRA and SRS, and the symbol - corresponds to unknown
bits of the shrunken sequence.
Computation of the SRA Initial State: According to Theorem 4.2, we compute the
positions of the (n
i
+ 1)-th elements of the first column of IC by solving the equation
system
n
i
· 15 ≡ mod 31 (i = 0,1, ..., 4).
That is to say, n
0
= 0,n
1
= 29,n
2
= 27,n
3
= 25,n
4
= 23. Then, by means of the char-
acteristic polynomial P
D
(x) we determine the values of the (n
i
+ 1)-th (i = 0,1,...,4)
elements of the first column {d
0
} of IC. Consequently, a
0
= 1,a
1
= 0,a
2
= 0,a
3
=
1,a
4
= 1 (see Table 1). Therefore, the initial state of the register SRA (1, 0, 0, 1, 1) has
been determined.
Computation of the SRS initial state: According to Theorem 4.3, we compute the
relative shifts between consecutive columns in the matrix IC:
- Computation of o1: We know a
1
at the (29+1)-th position of the first column fd0g
and compute its S−1= 4 successive bits. We compare these 5 bits (0, 0, 1, 1, 0) with the
first 5 bits (0, 0, 1, 1, 0) of the second column {d
1
} (see Table 1). There is coincidence,
thus o1 = 1.
- Computation of o2: We know a
2
at the (27+1)-th position of the {d
0
} and compute
its 4 successive bits. We compare these 5 bits (0, 1, 0, 0, 1) with the first 5 bits (1, 0, 0, 1,
0) of the third column {d
2
} . There is no coincidence, thus we analyze the following bit
a
3
.We know a
3
at the (25+1)-th position of {d
0
} and compute its 4 successive bits.We
compare these 5 bits (1, 0, 0, 1, 0) with the first 5 bits (1, 0, 0, 1, 0) of { d
2
} (see Table
1). There is coincidence, thus o
2
= 3. Since o
2
= 3 ≥ S − 1, we have determined the
initial state of SRS. In fact, s
0
= 1, o
1
= 1 implies s
1
= 1, o
2
= 3 implies s
2
= 0 and
s
3
= 1. Therefore, the SRS initial state is (s
0
,s
1
,s
2
,s
3
) = (1,1,0,1). Remark that only
the knowledge of three columns of the sub-matrix has been necessary to identify the
initial state of SRS. Indeed, this number equals the number of bits 1 in the initial state
of the selector register. The maximum number of known bits corresponds to SRS initial
state with all bits 1. In the remaining cases, less bits are sufficient.
Once the initial states of both register are determined, the whole shrunken sequence that
is the keystream sequence can be computed.
64

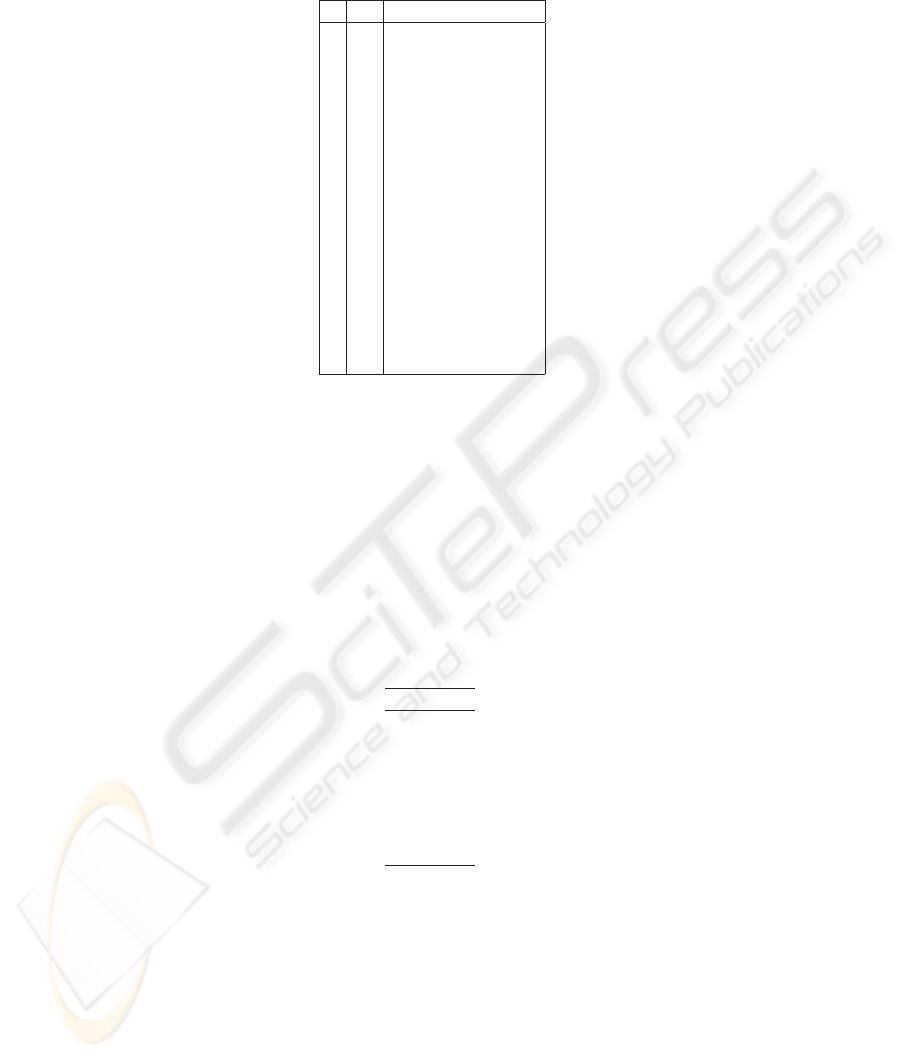
Table 1. Matrix IC corresponding to the described SG.
n
i
{a
i
} d
0
d
1
d
2
d
3
d
4
·· · d
7
0 a
0
1 0 1 1 - - -
1 1 0 0 1 - - -
1 1 0 0 1 - - -
2 0 1 0 1 - - -
3 0 1 1 1 - - -
4 0 0 0 1 - - -
5 - - - - - - -
·· · - - - - - - -
23 a
4
1 - - - - - -
24 - - - - - - -
25 a
3
1 - - - - - -
26 0 - - - - - -
27 a
2
0 - - - - - -
28 1 - - - - - -
29 a
1
0 - - - - - -
30 0 - - - - - -
5 Generalization to Interleaved Sequences
First of all, we introduce the general definition of interleaved sequence [12].
Definition 5.1. Let f (x) be a polynomial over GF(q) of degree r and let m be a positive
integer. For any sequence {u
k
} over GF(q), we write k = i·m+ j with (i = 0,1,...) and
( j = 0,...,m − 1). If every sub-sequence {u
j
} of {u
k
} defined as {u
i·m+ j
} is generated
by f(x), then the sequence {u
k
} is called an interleaved sequence over GF(q) of size m
associated with the polynomial f(x).
Table 2. Interleaved sequence with 4 shifted versions of the same PN-sequence.
u
o
u
1
u
2
u
3
1 1 1 1
1 0 1 0
0 0 1 1
0 1 0 1
1 0 0 1
0 1 1 0
1 1 0 0
Table 2 shows the interleaved sequence {u
k
} over GF(2) associated with the 3-
degree characteristic polynomial f(x) = x
3
+x+ 1 over GF(2) and size m = 4. Reading
by rows, the interleaved sequence is {u
k
} = {1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1,
1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0 } while by columns the sequence is made out of {u
j
}
( j = 0, ..., 3) four shifted versions of the PN-sequence generated by f(x).
Interleaved sequences are currently used as keystream sequences with application
in cryptography. They can be generated in different ways:
65

(1) By a LFSR controlled by another LFSR (which may be the same one) e.g. multi-
plexed sequences [11], clock-controlled sequences [1], cascaded sequences [7], shrink-
ing generator sequences [5] etc.
(2) By one or more than one LFSR and a feed-forward nonlinear function e.g. Gold-
sequence family, Kasami (small and large set) sequence families, GMW sequences,
Klapper sequences, No sequences etc. See [9] and the references cited therein.
In brief, a large number of well-known cryptographic sequences are included in
the class of interleaved sequences. Next, the link between interleaved sequences and
shrunken sequences is expressed in the following result.
Theorem 5.2. Shrunken sequences are interleaved sequences of size 2
(S−1)
.
Proof. Let {z
k
} be a shrunken sequence with characteristic polynomial P(x)
p
where
P(x) is an A-degree primitivepolynomial and p is an integer in the interval 2
(S−2)
< p ≤
2
(S−1)
. According to the interleaved configuration IC, we may express {z
k
} in terms of
m sequences {z
j
} where {z
j
} = {z
i·m+ j
} with i ≥ 0,m = 2
(S−1)
and ( j = 0,...,m −
1). Since by Theorem 3.2 the sequences {z
j
} are generated by the same characteristic
polynomial P
D
(x), we get that the shrunken sequence {z
k
} is an interleaved sequence
of size 2
(S−1)
associated with the polynomial P
D
(x). 
The previous theorem proves that shrunken sequences are interleaved sequences.
Moreover, section 4 shows that the knowledge of a number of bits of the shrunken
sequence allows us to mount a cryptanalytic attack against the shrinking generator.
As many cryptographic sequence generators produce interleaved sequences, then the
previous considerations take us into the following conjecture:
Conjecture 5.3. Given a number of bits corresponding to an initial sub-matrix of the in-
terleaved configuration IC of an interleaved sequence, it is possible to obtain the whole
interleaved sequence. The confirmation of this conjecture would prove the weakness of
interleaved generators for cryptographic purposes.
6 Conclusions
In this work a new cryptanalytic attack against the class of shrinking generators has
been proposed. The amount of intercepted bits necessary to realize such an attack is
much lesser than that of other standard cryptanalysis. The basic idea consists in defin-
ing the shrunken sequence as an interleaved sequence. Hence the weaknesses inherent
to interleaved sequences can be advantageously used in the practical attack. A direct
consequence of this technique is its generalization to other interleaved sequence gener-
ators of cryptographic purpose. In this way, the security of this kind of generators must
be carefully checked.
Acknowledgements
This work has been done in the frame of the project HESPERIA (http://www.proyecto-
hesperia.org) supported by CDTI under programme CENIT.
66

References
1. T. Beth, F. Piper, The Stop-and-Go Generator, in Proceedings of EUROCRYPT’84, in: Lec-
ture Notes in Computer Science, vol. 228, Springer Verlag, 1985, pp. 228-238.
2. Bluetooth, Specifications of the Bluetooth system,, available at http://www.bluetooth.com/
3. P. Caballero-Gil, A. F´uster-Sabater, A Wide Family of Nonlinear Filter Functions with a
Large Linear Span, Information Sciences, 164 (2004) 197-207.
4. P. Caballero-Gil, A. F´uster-Sabater, Using Linear Hybrid Cellular Automata to Attack the
Shrinking Generator, IEICE Transactions on Fundamentals of Electronics Communications
and Computer, E89-A (2006) 1166-1172.
5. D. Coppersmith, H. Krawczyk, H. Mansour, The Shrinking Generator, in Proceedings of
CRYPTO’93, in: Lecture Notes in Computer Science, vol. 773, Springer-Verlag, 1994, pp.
22-39.
6. A. F´uster-Sabater, Run Distribution in Nonlinear Binary Generators, Applied Mathematics
Letters 17 (2004) 1427-1432.
7. D. Gollmann, W.G. Chambers, Clock-Controlled Shift Register, IEEE J. Selected Areas
Commun 7 (1989) 525-533.
8. S.W. Golomb, Shift Register-Sequences, Aegean Park Press, Laguna Hill, 1982.
9. G. Gong, Theory and Applications of q-ary Interleaved Sequences, IEEE Trans. Information
Theory 41 (2) (1995) 400-411.
10. GSM, Global Systems for Mobile Communications, available at http://cryptome.org/gsm-
a512.htm
11. S.M. Jennings, Multiplexed Sequences: Some Properties, in Proceedings of EURO-
CRYPT’83, in: Lecture Notes in Computer Science, vol. 149, Springer Verlag, 1983, pp.
210-221.
12. S. Jiang, Z. Dai and G. Gong. On interleaved sequences over finite fields. Discrete Maths,
252 (2002) 161-178.
13. A. Kanso, Clock-Controlled Shrinking Generator of Feedback Shift Registers, in: Lecture
Notes in Computer Science, vol. 2727, Springer Verlag, 2003, pp. 443-451.
14. R. Lidl, H. Niederreiter, Introduction to Finite Fields and Their Applications, Cambridge
University Press, 1986.
15. R.L. Rivest, RSA Data Security, Inc., March 12, 1998.
16. I. Shparlinski, On Some Properties of the Shrinking Generator, Designs, Codes and Cryp-
tography 23 (2001) 147-156.
17. L. Simpsom, J. Golic, E. Dawson, A Probabilistic Correlation Attack on the Shrinking Gen-
erator, in Proceedings of EUROCRYPT’98, in: Lecture Notes in Computer Science, vol.
1438, Springer Verlag, 1998, pp. 147-158.
67