
Robust Pattern Recognition with Nonlinear Filters
Saúl Martínez-Díaz and Vitaly Kober
Department of Computer Science, Division of Applied Physics, CICESE
Km 107 Carretera Tijuana-Ensenada, Ensenada, B.C. 22860, México
Abstract. Nonlinear composite filters for robust and illumination-invariant pat-
tern recognition are proposed. The filters are based on logical and rank order
operations. The performance of the proposed filters is compared with that of
various linear composite filters in terms of discrimination capability. Computer
simulation results are provided to illustrate the robustness of the proposed fil-
ters when a target is embedded into cluttered background with unknown illumi-
nation and corrupted by additive and impulsive noise.
1 Introduction
Correlation-based filters have been an area of extensive research over past decades
[1-4]. A usual way to design filters is by optimizing some performance criteria. Vari-
ous performance measures for correlation filters have been proposed and summarized
[1]. For example, the classical matched spatial filter (MSF) [2] is optimal if an input
image is corrupted by additive Gaussian noise. However, many real images are cor-
rupted by non-Gaussian noise. Besides, the MSF is not able to discriminate effec-
tively an object of one class and that belonging to other classes. Composite filters
based on synthetic discriminant functions (SDF) [3] can be used for multiclass pattern
recognition. SDF filters utilize a set of training images to synthesize a template that
yields prespecified correlation outputs in response to training images. A drawback of
SDF filters is appearance of false peaks on the correlation plane. A partial solution of
this problem is to control the whole correlation plane by minimizing the average
correlation energy (MACE) [4]. MACE filters suppress sidelobes while produce
sharp correlation peaks at the target location. However, the filters are not tolerant to
input noise.
Traditionally correlation-based filters use a linear correlation operation. Minimiza-
tion of the mean absolute error (MAE) leads to a nonlinear correlation, which is com-
puted as a sum of minima. The MAE criterion is often used to solve optimization
problems in rank-order image filtering. This criterion is more robust when the noise
has even slight deviations from the Gaussian distribution, and produces a sharper
peak at the origin.
5
Recently, local adaptive correlations based on rank order opera-
tions were proposed to improve recognition in scenes with non-Gaussian noise [6,7].
However, their performance is poor in scenes with highly illuminated background.
In this paper we propose illumination-invariant nonlinear composite filters derived
from the MAE criterion. With the help of computer simulations the performance of
Martínez-Díaz S. and Kober V. (2008).
Robust Pattern Recognition with Nonlinear Filters.
In Proceedings of the 8th International Workshop on Pattern Recognition in Information Systems, pages 223-230
Copyright
c
SciTePress

the proposed filters is compared with that of linear composite filters. The paper is
organized as follows: Section 2 provides a review of composite linear filters. Section
3 introduces the proposed filters. In section 4 we provide computer simulation results.
Section 5 summarizes our conclusions.
2 Linear Composite Filters
Composite filters are usually used for distortion-invariant pattern recognition. In this
case a set of training images that are sufficiently descriptive and representative of
expected distortions can be employed to improve the recognition.
2.1 SDF filter
Conventional SDF filters are a linear combination of MSFs for different patterns. The
coefficients of the linear combination are chosen to satisfy a set of constraints on the
filter output requiring a prespecified value for each pattern used.
Suppose there are N training images from a true class, each image contains d pix-
els. We convert the 2D arrays of the images into the 1D column vector by lexico-
graphical ordering. These vectors are the columns of a matrix R of size d×N. The
column vector u contains N elements, which are the desired values of the output cor-
relation peaks corresponding to each training image. If the matrix (R
+
R) is nonsingu-
lar, the conventional SDF filter can be expressed as follows [3]:
hRRRu
SDF
+−
=
1
() ,
(1)
here superscript + means conjugate transpose. The main shortcoming of the linear
SDF filters is appearance of sidelobes owing to the lack of control over the whole
correlation plane.
2.2 MACE filter
In order to suppress false correlation peaks, the MACE filter minimizes the average
correlation energy of the correlation outputs for a set of training images, satisfying at
the same time the correlation peak constraints at the origin. Suppose that there are N
training images, each image with d pixels. First, the 2D Fourier transform is per-
formed on each training image and converted into 1D column vector. Then, a matrix
X with N columns and d rows is constructed. The columns of X are given by the
vector version of each transformed image. The frequency response of the MACE
filter can be expressed as [4]
-1 + -1 -1
hDX(XDX)u
MACE
=
,
(2)
where the column vector u contains desired correlation peak values of the training
images and the
dxd diagonal matrix D contains the average power spectrum of the
training images.
224

3 Nonlinear Composite Filters
We wish to design a nonlinear composite filter, which is invariant to illumination,
robust to noise, cluttered background, and false objects. The proposed filtering is a
locally adaptive processing of the signal in a moving window. The moving window is
a spatial neighborhood containing pixels surrounding the central window pixel geo-
metrically. The neighborhood is referred to as the
W-neighborhood. The shape of the
W-neighborhood is similar to the region of support of the target. The size of the
neighborhood is referred to as
W , and it is approximately taken as the size of the
target. In the case of nonstationary noise or cluttered background (space-varying
data), it is assumed that the
W-neighborhood is sufficiently small and the signal and
noise can be considered stationary over the window area.
3.1 Illumination-Invariant Correlation
Let {T(k,l)} and {S(k,l)} be a target image and a test scene respectively, both with Q
levels of quantization. Here
(k,l) are the pixel coordinates. The local nonlinear corre-
lation derived from the MAE criterion between a normalized input scene and a shifted
version of the target at coordinates (
k,l) can be defined as
() ()( )()( )
,
,,,,,,
mn W
Ckl MINaklSm kn l bkl Tmn
∈
=+++
⎡⎤
⎣⎦
∑
,
(3)
where the sum is taken over the
W-neighborhood. The coefficients a(k,l) and b(k,l)
take into account unknown illumination and a bias of the target respectively. The
normalization coefficients can be computed by minimizing the mean squared error
between the window signal and the target as:
()
()( )
()
()
()
()
()
,
2
2
,
,, ,
,
,,
mn W
mn W
Tmn Sm kn l WT Skl
akl
Sm kn l W Skl
∈
∈
⋅++−⋅⋅
=
++−⋅
∑
∑
,
(4)
()
(
)
(
)
,,,bkl T akl Skl=− ⋅
,
(5)
here
T and
(
)
,Skl are the average of the target and local window signal over the W-
neighborhood at the (
k,l)’th window position, respectively.
3.2 Nonlinear Composite Correlation Filters
According to the threshold decomposition concept [8], a gray-scale image X(k,l) can
be represented as a sum of binary slices:
1
1
(,) (,)
Q
q
q
X
kl X kl
−
=
=
∑
,
(6)
225

where
{}
(,), 1,... 1
q
Xklq Q=− are binary slices obtained by decomposition of the
image with a threshold q as follows:
1, ( , )
(,)
0,
q
if X k l q
Xkl
otherwise
≥
⎧
=
⎨
⎩
.
(7)
Now, assume that there are N objects from the true class
(
)
{
}
,, 1...
i
Tkli N= and M
objects to be rejected
()
{}
, , 1...
i
P
kl i M= (the false class). We construct N reference
images as logical combinations of the training images:
() () ()
1
1
1
ˆ
, , , , 1...
Q
M
qq
ii j
q
j
Tkl T kl P kl i N
−
=
=
⎡⎤
==
⎢⎥
⎢⎥
⎣⎦
∑ IU
,
(8)
where
{}
(,), 1,... 1, 1,...
q
i
Tklq Q i N=−= and
{
}
( , ), 1,... 1, 1,...
q
i
Pklq Q i M=−= are
binary slices obtained by threshold decomposition from corresponding training im-
ages of true and false classes respectively.
U
and
I
represent the logical union
and intersection, respectively. Finally, the nonlinear composite correlation is com-
puted by
() ()
ˆ
,,,1...
i
i
u
Ckl MAX C kl i N
t
⎛⎞
⎧
⎫
==
⎜⎟
⎨
⎬
⎜⎟
⎩⎭
⎝⎠
.
(9)
where
()
ˆ
,Ckl
is the composite correlation at the coordinates (k,l),
(
)
,
i
Ckl is the i’th
correlation (see equation 3) between the input scene and the i’th reference image
(computed with equation 8), MAX (X
i
) is the maximum value among all the X
i
, u is
the desired value at the correlation output, and
() ()
1
,1
1
,,
Q
M
qq
ii j
kl Wq
j
tTklPkl
−
∈=
=
⎡
⎤
=
⎢
⎥
⎢
⎥
⎣
⎦
∑∑ IU
.
One can show that the composite correlation yields the value u at output correlation
for objects belonging to the true class, while the output correlation peaks for the false
objects are zeros.
4 Computer Simulations
In this section computer simulation results obtained with the proposed filters are pre-
sented. The performance of nonlinear filters is compared with that of SDF and
MACE filters in terms of discrimination capability (DC). The DC is formally defined
as the ability of a filter to distinguish a target among other different objects [9], and
can be expressed as:
()
()
2
2
00
1
00
B
O
C,
DC
C,
=−
,
(10)
226

where C
B
(0,0) is the maximum in the correlation plane over the background area to
be rejected and C
O
(0,0) is the maximum in the correlation plane over the area of the
object to be recognized. The area of the object to be recognized is determined by the
region of support of the target. The background area is complementary to the area of
the object to be recognized.
(a) (b)
Fig. 1. (a) Objects used in experiments (target is marked with the arrow), (b) test scene with
objects embedded into a cluttered background.
Figure 1(a) shows the objects used in computer simulations. The target is marked
with an arrow. The size of the moving window is about 19×35 pixels. The signal
range of images is [0-255]. The objects of the true class are the target and its version
rotated by 5 degrees. Figure 1(b) illustrates the objects embedded into a background.
The size of scenes is 256x256.The mean of target is 92.3 and its standard deviation is
47.9. The mean of background is 93.8 with standard deviation of 48.7. We designed a
filter with 2 objects from the true class and 1 object from the false class. 30 statistical
trials in different positions of the objects were conduced and averaged. The DC val-
ues for the SDF, the MACE and the nonlinear filter are 0.13, 0.90, and 0.93, respec-
tively.
Next the mean of background is varied while its standard deviation is fixed. Figure
2 shows the results. Note that the performance of linear filters deteriorates quickly
when the background becomes highly illuminated, while the proposed nonlinear filter
is illumination-invariant. The SDF filter fails to recognize the target in highly illumi-
nated background.
227

25 50 75 100 125 150 175 200 225 250
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Mean of background
Discrimination Capability
Nonlinear filter
MACE filter
SDF filter
Fig. 2. Performance of filters in terms of DC as a function of the mean of background.
Now we show the robustness of filters to different kinds of noise. First, the scene is
corrupted by impulsive salt and pepper noise. The probability of impulsive noise is
varied from 0.04 to 0.2 with equal probability of occurrence for negative and positive
impulses. To guarantee statistically correct results, 30 statistical trials of each experi-
ment for different realizations of random processes were performed. Figure 3(a) is an
example of the test scene corrupted by impulsive noise with probability of 0.2.
(a) (b)
Fig. 3. Test input scene corrupted by (a) impulsive noise with probability of 0.2, (b) mixed
additive noise with standardp deviation of 40 and impulsive noise with probability of 0.2.
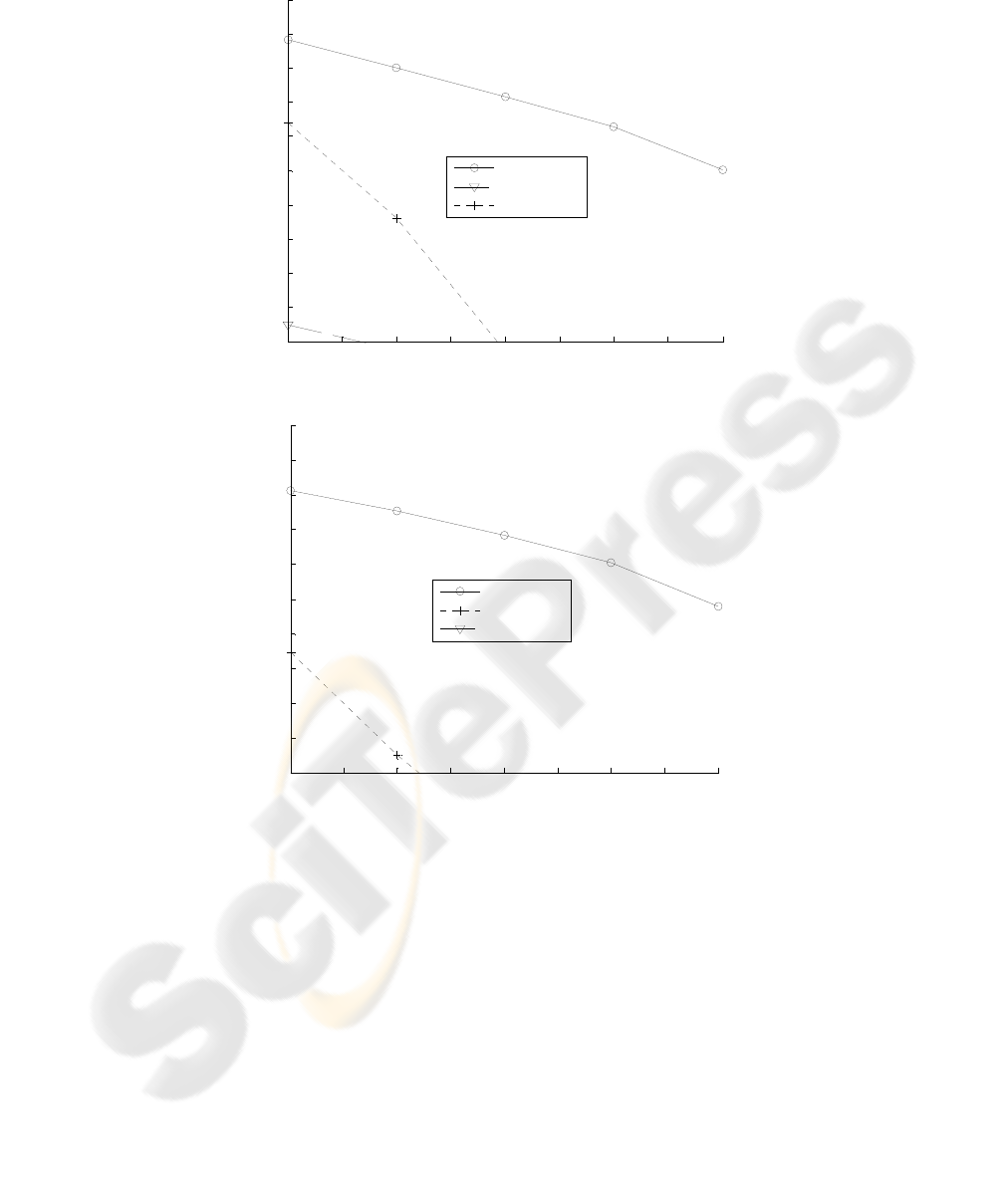
Figure 4(a) illustrates the performance of filters as a function of the probability of
impulsive noise.
228
0.04 0.08 0.12 0.16 0.2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Prob. of impulsive noise
Discrimination Capability
Nonlinear filter
SDF filter
MACE filter
(a)
0.04 0.08 0.12 0.16 0.2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Prob. of impulsive noise
Discrimination Capability
Nonlinear filter
MACE filter
SDF filter
(b)
Fig. 4. Performance of filters in terms of DC as a function of impulsive noise probability for (a)
impulsive noise only, (b) mixed additive and impulsive noise.
Note that performance of linear filters degrades rapidly, while the proposed filter is
able to recognize targets. Finally the scene is corrupted by mixed additive Gaussian
and impulsive noise. The standard deviation of additive noise is 40 and the probabil-
ity of impulsive noise is varied from 0.04 to 0.2.
Figure 3(b) shows an example of a test scene corrupted with mixed noise, the prob-
ability of impulsive noise is 0.2. Figure 4(b) shows the computer simulation results. It
229

can be seen that the linear filters rapidly fail to recognize the objects, while the
nonlinear filter is able to correctly detect objects in extremely noisy scenes.
5 Conclusions
In this paper, composite nonlinear filters were proposed. Their recognition perform-
ance and noise robustness were compared to those of composite linear filters in terms
of discrimination capability. Extensive computer simulations illustrated an improve-
ment in pattern recognition of multiple objects when the proposed filters are used.
References
1. Vijaya-Kumar, B. V. K., Hassebrook, L.: Performance Measures for Correlation Filters.
Appl. Opt. Vol. 29 No. 20. (1990) 2997-3006.
2. VanderLugt, A. B.: Signal Detection by Complex Filtering. IEEE Trans. Inf. Theory. Vol..
10. (1964) 139-135.
3. Hester, C. F., Casasent, D.: Multivariant Technique for Multiclass Pattern Recognition.
Appl. Opt. Vol.19 No. 11. (1980) 1758-1761.
4. Mahalanobis, A., Vijaya-Kumar, B. V. K., Casasent, D.: Minimum Average Correlation
Energy Filters. Appl. Opt. Vol. 31. (1987) 1823-1833
5. Maragos, P.: Morphological Correlation and Mean Absolute Error Criteria. Proc. conf. IEEE
Trans. Acoust. Speech Signal Process. (1989). 1568-1571
6. Kober, V., Alvarez-Borrego, J., Ovseyevich, I.A.: Adaptive Rank Order Correlations. Pat-
tern Recognition and Image Analysis. Vol. 14 No. 1. (2004) 33-39.
7. Kober, V., Mozerov, M., Alvarez-Borrego, J. Pattern Recognition Based on Rank Correla-
tions. Applications of Digital Image Processing, Proceedings of SPIE. Vol. 5558. (2004)
99-104
8. Fitch, J.P., Coyle, E.J., Gallagher, N.C. Jr.: Median Filtering by Threshold Decomposition.
IEEE Trans. Acoust. Speech Signal Process. (1984) 1183-1188.
9. Yaroslavsky, L. P.: The Theory of Optimal Methods for Localization of Objects in Pictures.
In: Progress in Optics XXXII, E. Wolf, Ed.., Elsevier. (1993) 145-201.
230
