The Linear Conditional Probability Matrix Generator

for IT Governance Performance Prediction

Mårten Simonsson, Robert Lagerström and Pontus Johnson

Department of Industrial Information and Control Systems

Osquldas väg 12, KTH, Royal Institute of Technology, 100 44 Stockholm, Sweden

Abstract. The goal of IT governance is not only to achieve internal efficiency

in an IT organization, but also to support IT’s role as a business enabler. The

latter is here denoted IT governance performance, and cannot be controlled by

IT management directly. Their realm of control includes IT governance matur-

ity, indicated by e.g. different IT activities, documents, metrics and roles. Cur-

rent IT governance frameworks are suitable for describing IT governance, but

lack the ability to predict how changes to the IT governance maturity indicators

affect the IT governance performance. This paper presents a Bayesian network

for IT governance performance prediction, learned with experience from 35

case studies. The network learns using the proposed Linear Conditional Prob-

ability Matrix Generator. The resulting Bayesian network for IT governance

performance prediction can be used to support IT governance decision-making.

1 Introduction to IT Governance

The concept of IT governance emerged in the nineties. Hendersen & Venkatraman [6]

and Loh & Venkatraman [15] then used the term to describe the array of interfirm

relationships involved in achieving strategic alignment of business and IT. Effective

IT governance provides mechanisms that enable IS/IT management to develop inte-

grated business and IT plans, allocate responsibilities, and prioritize IT initiatives

[12], [23], [29]. It is important to ensure that the IT governance is not only designed

to achieve internal efficiency in the IT organization, such as deploying good IT proc-

esses and making sure that the means and goals are documented. The final goal of

good IT governance is to provide the business with the best support needed in order

to conduct business in a good manner. The IT governance mechanisms should be

chosen so that the impact on the business is maximized. There are many activities in

the IT organization that can be changed, but clearly, not all changes affect the busi-

ness in a positive way. From an IT manager’s point of view, it would be of great

interest to know what impact each change made to the IT organization would have on

the business, in order to choose the most beneficial way to govern IT.

There already exist several frameworks aiming to support IT governance. Weill &

Ross have developed an IT governance framework based on just a few questions that

can be used to assign responsibilities for high level IT decision making, but their

work gives no further guidance on how the IT organization should actually transform

theory into practice [30]. The ISO/IEC 20000 and its predecessor IT Infrastructure

Simonsson M., Lagerström R. and Johnson P. (2008).

The Linear Conditional Probability Matrix Generator for IT Governance Performance Prediction.

In Proceedings of the 6th International Workshop on Modelling, Simulation, Veriﬁcation and Validation of Enterprise Information Systems, pages

170-179

DOI: 10.5220/0001736301700179

 SciTePress

Library (ITIL) might aid the creation of processes related to delivery and support

[8],[19], [20]. ITIL also details establishment and maintenance of service level

agreements (SLA). ITIL has traditionally provided little support for strategic IT con-

cerns. However, this has been improved in recent ITIL v3 publications. Currently, the

Control Objectives for Information and related Technology (COBIT) is most well-

known framework for IT governance improvement, risk mitigation, IT value delivery

and strategic alignment maturity assessments [2], [5], [7], [22], [28]. The COBIT

framework was first issued by the IT Governance Institute, ITGI, in 1998 [9]. It de-

scribes the IT organization by means of 34 processes, within four domains: Plan &

Organize, Acquire & Implement, Deliver & Support, and Monitor & Evaluate. A

recent addition to COBIT is the Val IT framework, taking IT governance onto a

higher level of abstraction by providing general directions on how to manage IT from

a business point of view [10].

In this paper, the term IT governance performance is used to describe the good-

ness of an enterprise’s IT organization from a business point of view. The frame-

works presented in the paragraph above are mainly of descriptive nature, i.e. they

describe the state of an IT organization according to best practice on IT governance

or IT management. None of them has however the ability to foresee how the IT gov-

ernance performance is linked to the maturity of the IT organization in terms of its

activities, level of documentation, etc. The purpose of this paper is to propose a

method for prediction of IT governance performance within an enterprise. In particu-

lar, by using such method, it is possible to compare the current state with future sce-

narios. For instance, if the decision-making authority for acquisition of commodity

software is moved from business unit level to IT operations level, how would that

affect the IT governance performance? Making such predictions also enables pre-

scription, i.e. not only evaluating different scenarios, but also to chose rationally

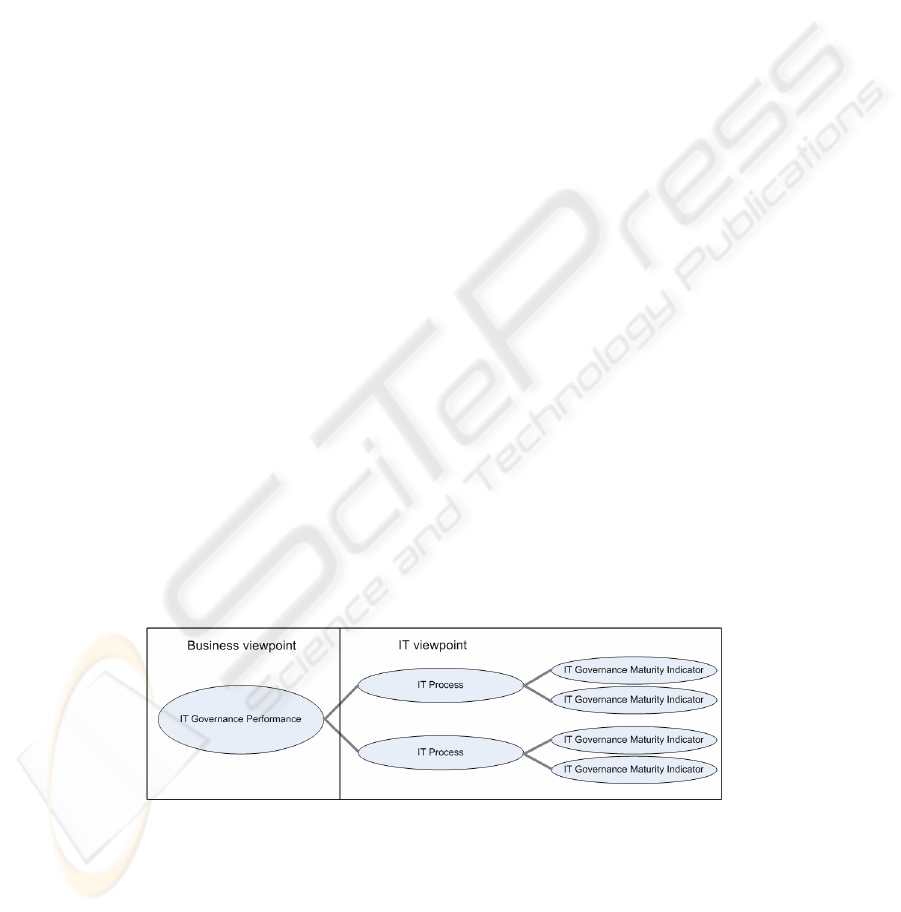
between them. Fig. 1 shows a conceptual view of the model for IT governance per-

formance prediction proposed in this paper. On the left side, there is the actual, intrin-

sic, IT governance performance, as seen from the business point of view. Clearly, the

aim of any organization would be to improve the IT governance performance to in-

crease stakeholder satisfaction and make sure that business runs as smoothly as possi-

ble. The IT governance performance is not directly controllable by IT management, but

IT processes for e.g. hardware acquisition, IT project management and IT strategy are in

the realm of control.

Fig. 1. The conceptual model for IT governance performance prediction. The IT governance

performance, as seen from the business viewpoint, is not directly controllable. Within the

realms of control for IT management are IT processes and IT governance maturity indicators.

171

Such IT processes are difficult to measure directly, but they comprise numerous

and measurable IT governance maturity indicators, including maturity of individual

IT related activities, level of monitoring, level of documentation, level of role as-

signment, etc. It is reasonable to believe that some of the IT governance maturity

indicators are correlated with the intrinsic IT governance performance, even though it

might be hard to establish the strength of the correlation. A model for prediction of IT

governance performance would need to take into account and define the impact of

each one of the IT governance performance indicators.

Several prediction methods are used in the research community today, including

Dempster-Shafer, Bayesian networks, neural networks, and multivariate analysis. Of

the above presented methods, Bayesian networks fulfill most requirements as pre-

sented in [12]. Therefore, such networks are used for IT governance maturity predic-

tion in this paper.

2 Bayesian Networks

Friedman describes a Bayesian network, B=(G, P), as a representation of a joint prob-

ability distribution, where G=(V, E) is a directed acyclic graph consisting of vertices,

V, and edges, E [3],[4]. The vertices denote a domain of random variables X

,…, X

also denoted chance nodes. Each chance node, X

, may take on a value x

from the

finite domain Val(X

). The edges denote causal dependencies between the nodes, i.e.

how the nodes relate to each other. The second component, P, of the network B, de-

scribes a conditional probability distribution for each chance node, P(X

), given its

parents Pa(X

) in G. It is possible to write the joint probability distribution of the

domain X

,…, X

using the chain rule of probability, in the product form

() ()()

∏

iin

XPaXPXXP

|,...,

In order to specify the joint distribution, the respective conditional probabilities that

appear in the product form must be found. The second component P describes distri-

butions P(x

| pa(X

)) for each possible value x

of X

, and pa(X

) of Pa(X

), where

pa(X

) is the set of values of Pa(x

). These conditional probabilities are represented in

matrices, here on called conditional probability matrices (CPMs). Using a Bayesian

network, it is possible to answer questions such as what is the probability of X = x

given that Y = y

and Z = z

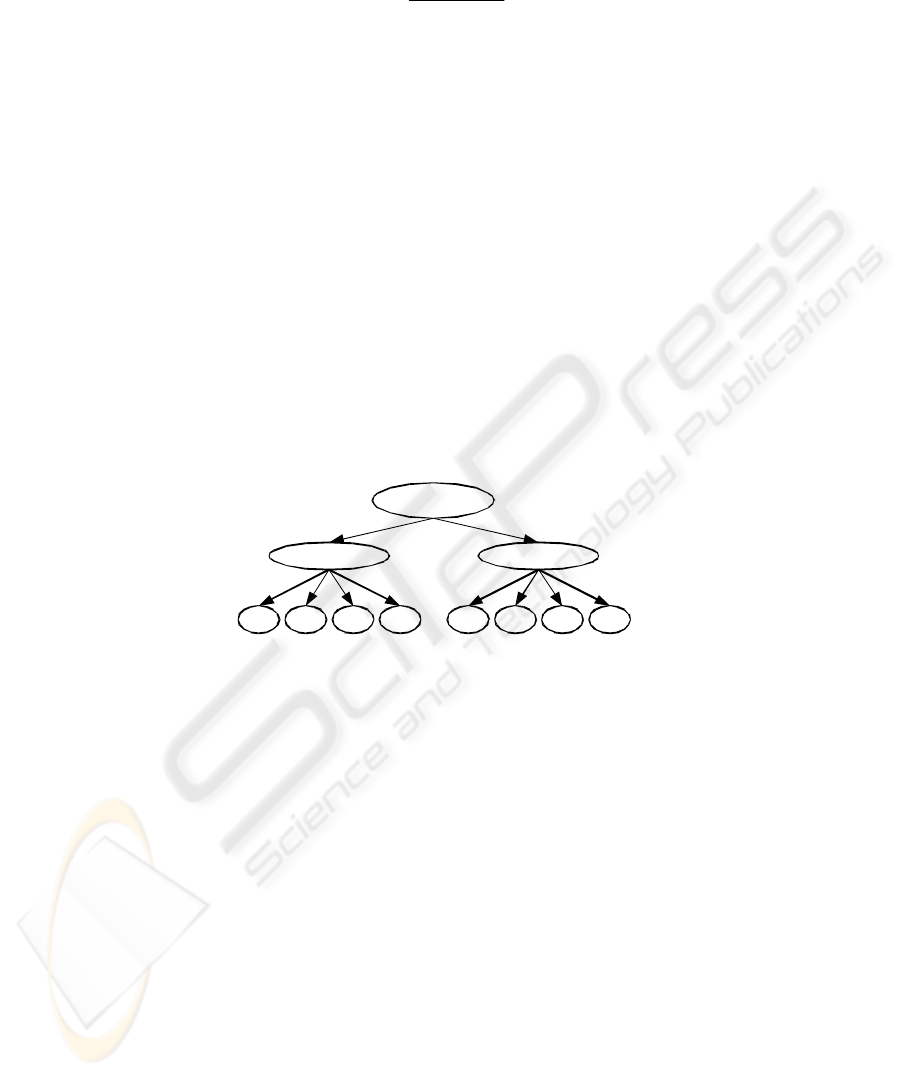
. An example of a Bayesian network and a CPM repre-

senting the chance nodes X, Y, and Z is shown in Fig.

2. The CPM next to the network

answers the question

()

121

,| zyxP

stated above. More comprehensive treatment on

Bayesian networks can be found in the literature [11], [18], [21], [24]. The generic

process for constructing Bayesian networks consists of three steps to define the nodes,

relations and conditional probability matrices. These are described in the context of IT

governance performance prediction in the following sections.

Y Z

P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)P(x

| y

)

Fig. 2. A Bayesian network and the conditional probability matrix for X given Y and Z.

172

3 Defining Nodes

It was decided to base the predictive Bayesian network on COBIT, as the framework

provides the most relevant and detailed support for IT governance. The motivation for

this choice can be found in previous publications [25], [26].

The concept of IT governance as consisting of processes, activities, roles, docu-

ments and metrics was adopted from COBIT. The use of processes to describe an IT

organization is commonly employed in many frameworks, and is also used in the

herein proposed approach. Further, each process contains one or more activities,

which represent the actual content of the work performed within the IT organization.

The documents correspond to process inputs and outputs as stated in COBIT. Metrics

are used to monitor the execution of each process, and a representation for metrics

monitoring is also incorporated. The concept of Roles being responsible, accountable,

consulted or informed on the execution of different activities is also incorporated. The

role representation features the distinction between executives, business and IT as

stated by Weill & Ross and IT Governance Institute, [10], [30] but also employs IT

operations and audit roles taken from COBIT [9].

Indicators for IT governance maturity, as seen from IT’s viewpoint, can be ob-

tained by gathering information on the above mentioned entities for each IT process.

Then, the activity execution (A), metrics monitoring (M), documents in place (D),

and the responsibility assignment (R) can be evaluated according to previous work by

Simonsson [26]. These four are represented as chance nodes with maturity levels

ml0-ml5 in the Bayesian network for IT governance performance prediction. The

entire IT organization is represented by means of 136 different nodes, so called IT

governance maturity indicators, that together form the 34 processes detailed in

COBIT. As mentioned earlier the purpose of the Bayesian network is not solely to

study the IT organization in terms of controllable maturity indicators bur also to pre-

dict the uncontrollable business perception of IT governance performance by study-

ing the controllable IT governance maturity indicators, cf. Fig. 1. Weill & Ross have

previously determined IT governance performance in 250 organizations by means of

letting senior management judge their organization’s performance with respect to two

objectives [30], cf. Table 1. The same objectives have been used in the research pre-

sented in this paper.

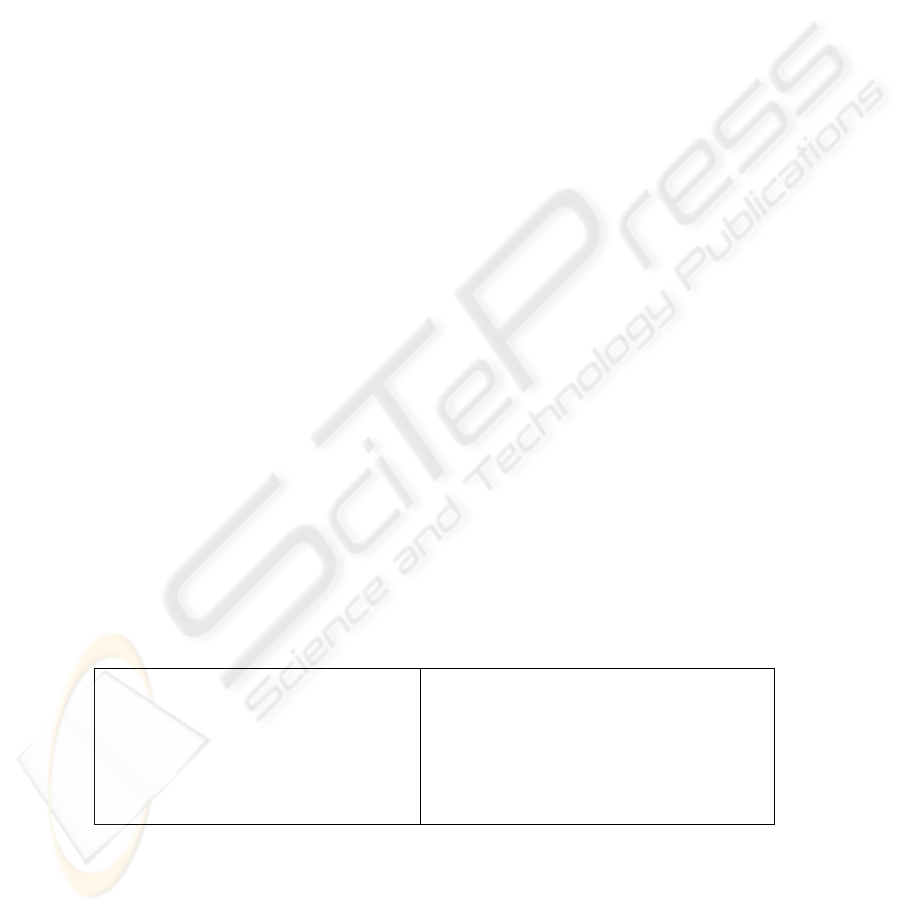
Table 1. Objectives employed in order to represent the IT governance performance node

in the Bayesian network [30].

O1. How important are the following outcomes

of your IT governance, on a scale from 1 (not

important) to 5 (very important)?

Cost effective use of IT

Effective use of IT for growth

Effective use of IT for asset utilization

Effective use of IT for business flexibility

O2. What is the influence of IT governance in your

business on the following measures of success, on a

scale from 1 (not successful) to 5 (very successful)?

Cost effective use of IT

Effective use of IT for growth

Effective use of IT for asset utilization

Effective use of IT for business flexibility

Weill & Ross’ objectives were aggregated and transformed into performance levels

pl0-pl5 for the node ITG_Performance according to Formula (1).

173

⎟

⎠

⎞

⎜

⎝

⎛

−=

∑

2*1

25.1_

ePerformancITG

(1)

4 Defining Relations

In order to use a Bayesian network for predictions, not only knowledge about differ-

ent nodes and their maturity levels or intrinsic performance levels is needed. It is also

necessary to define how the nodes are related. The processes in COBIT well delimit

the scope of the work performed by the IT organization [26]. The IT processes are

controllable by IT management, and it is reasonable to believe that the maturity of an

IT process is causally linked to the IT governance performance, but the IT processes

are not measurable. However, each process consists of different activities, documents,

metrics, roles and responsibilities. These are controllable by IT management and

measurable in terms of IT governance maturity indicators. A causal relation exists

between the IT governance maturity indicators, and the IT processes.

By determining only the maturity of one or more of the indicators as discussed in

Section 3, the network can predict IT governance performance, which is the idea

behind the Bayesian network, cf. Fig.

3. The strength of the causal relations in the

network is mathematically described as CPMs.

PO1_ITProcessMaturity

ITG_Performance

ME4_ITProcessMaturity

PO1_A PO1_M PO1_D PO1_R ME4_A ME4_M ME4_D ME4_R

...

Fig. 3. The Bayesian network for IT governance maturity prediction features

34 IT Process Maturity nodes ranging from PO1 to ME4 [9].

5 Defining Conditional Probability Matrices

The CPMs defining the chance nodes in the network must be learned, i.e. the parame-

ters in the matrices need to be determined. The basic approach is to collect empirical

data for the nodes by conducting case studies and then use Bayesian network learning

algorithms to assign the parameters to the matrices.

5.1 Requirements on Methods for Learning Bayesian Networks

There are several methods for learning Bayesian networks. This subsection presents a

set of requirements that has been used in order to evaluate the four methods in focus

of this paper. Performing case studies is a time consuming activity, which is also

highly dependent on the number of accessible cases. The amount of data sets that the

174

network can learn from is often limited. Therefore, the learning method must be able

to obtain conditional probabilities based on a fairly small number of datasets. As

discussed previously, the structure of the network has already been determined and a

learning method should not change it. In other words, the user herself should be able

to choose network structure. The desired ability to learn conditional probabilities

without changing the structure of the network is denoted parameter learning. Finally,

it is deemed that the output of the method should be a conditional probability matrix.

5.2 Evaluation of Methods for Learning Bayesian Networks

Four methods have been evaluated, including the Expectation Maximization (EM), B-

Course, Path Condition (PC), and the Necessary Path Condition (NPC) algorithms.

The evaluation is focused on the requirements presented in the previous subsection,

namely support for learning from a limited number of data sets, parameter learning,

user choice of structure, and method outcome.

The most common method for learning Bayesian networks with statistical data is

called the EM algorithm [3],[14]. The main disadvantage with EM learning is that,

when using only a small number of datasets, the learning will result in conditional

probability matrices with zero entries. This means that if a set of values has not ap-

peared in any of the learning cases, the set cannot be used for prediction.

B-course is a web-based online data analysis method proposed by Myllymäki [17]

that allows the user to analyze data for multivariate probabilistic dependencies. The

outcome of the method is a Bayesian network structure with learned conditional

probability matrices. The main drawback with this method is that it learns the struc-

ture from data. It is not possible to force an already set structure upon B-course and

only learn the parameters of the variables. B-course also requires large number of

datasets to provide useable conditional probability matrices.

The PC algorithm is a constraint-based learning algorithm. This means that the al-

gorithm uses statistical tests to derive a set of conditional independent and dependent

statements, and learns the structure of a Bayesian network. The NPC algorithm is an

enhancement of the PC algorithm which intends to bridge the latter’s deficiencies in

learning from small number of data sets. Both algorithms have the disadvantage that

their outcomes are structures and not CPMs [16].

To summarize, the main requirement is that the method should be able to learn pa-

rameters based on collected data, which excludes the PC and NPC algorithms. Since

data collection in the case of IT governance performance prediction is made through

case studies, a key requirement is the limited amount of data sets available. Neither

the EM algorithm nor B-course addresses this issue. The result of the evaluation of

the methods and the proposed approach is visualized in Table 2. Linear regression is a

commonly used method for prediction of the outcome of one variable based on the

information of other variables [1],[27]. It may thus also be appropriate for learning

conditional probability matrices in Bayesian networks. The main weakness of this

approach is that the outcome of a linear regression is not a conditional probability

matrix, but rather an equation y=ax+b. However, if the outcome of linear regression

could be translated into a CPM, the approach would be appropriate for our purposes.

175

5.3 The Linear Conditional Probability Matrix Generator

Unfortunately, no linear learning approach with conditional probability matrices as

outcome exists in the readily available tools for Bayesian statistics. Therefore, the

Linear Conditional Probability Matrix Generator (LCPMG) was developed. In gen-

eral, LCPMG takes into account gathered observation data, processes it, and returns a

conditional probability matrix made with an assumption of linearity in the input data.

The generator works according the following steps:

Observations on a quantitative scale of measurement are made and a structure is

decided upon. For pedagogic purposes, assume 20 observations of the variable

and 20 simultaneous observations of

. The nodes

and

are causally related to

one another in the network,

affecting

. The observed values are on a continuous

scale

[]

5...0∈

and

[]

5...0∈

. The choice of scales of measure is due to the equally

graded scales for IT governance maturity assessment used in the COBIT framework [9].

A linear regression on the observations is performed according to standard proce-

dures described by e.g. Cohen and Walsh [1],[27]. The result is an equation

baXY

estimate

, where a and

are scalar constants. The residuals constitute the

difference between the linear approximation that is fitted to the observations

()

YX ,

and the actual observations

estimate

YYR

−

. The standard deviation S of the residuals,

an approximation of the certainty with which the linear approximation is made, is

calculated. The purpose of the LCPMG is to generate a discrete CPM from a continu-

ous linear approximation

estimate

Y . In order to do that, six different ranges for y

are

created:

5.55.45.35.25.15.05.0

543210

≤

<≤<≤− yyyyyy

[]

5,4,3,2,1,0

∈

Based on the linear approximation and the standard deviation S, the probability mass

P(y

| x

) in each cell of the CPM is calculated. The total probability

1)|(

∑

xyP

for each

[]5,4,3,2,1,0

∈

. As an example, if the linear approximation is

15.0 += xy

estimate

, and the standard deviation for the residual vectors equals

5.0

, this

corresponds to P(

) = 68.27 % [1]. In summary, the LPCMG has now trans-

formed two arrays with observations on a continuous scale, to a CPM describing the

causal relation between two nodes in a Bayesian network. Returning to the require-

ments on methods for learning Bayesian networks and comparing the LCPMG to

other already available methods one finds that the LCPMG fulfills all four require-

ments. Table 2 shows a final comparison of some common learning approaches for

Bayesian networks and the here proposed LCPMG.

Table 2. A comparison of different learning approaches for Bayesian networks.

Requirement

Method

EM Algorithm B-Course PC Algorithm NPC Algorithm LCPMG

ĆĆ

ĆĆ Ć

ĆĆ

CPM CPM & Structure Structure Structure CPM

Support for learning from a

limited number of data sets

User choice of structure

Method outcom e

Param eter learning

176

5.4 Using LCPMG for Creation of a Bayesian Network for IT Governance

Performance Prediction

The LCPMG is suitable for generating the CPMs of nodes that are linearly related to

one another. In the case of IT governance maturity prediction, the Bayesian network

has three hierarchical levels. The first level contains the measureable, yet not control-

lable IT governance performance node. The second level contains 34 IT process

nodes that are controllable, but not measureable. On the third level, 136 measureable

and controllable IT governance maturity indicator nodes reside, cf. Fig. 1. The CPMs

of all nodes at all levels must be defined, and the LCPMG can be applied stepwise in

order for the network to learn the CPMs.

Calculate the regressions for all IT governance maturity indicator nodes and the IT

governance performance node. Use the regressions to assign normalized weights w

each of the four node types; activities, metrics, documents and responsibilities.

The maturity for an IT process, m

, can be calculated as

prpdpmpap

rmlwdmlwmmlwamlwm _*_*_*_* +++=

. Calculate the m

for each of the

N*34 IT processes, where N represents the number of different observations made.

Use LCPMG to determine the CPMs for each of the 34 IT process nodes, based on

the m

:s and the ITG_Performance node. Use LCPMG to determine the CPMs for

each of the 136 maturity indicator nodes, based on maturity levels for the maturity

indicators, and the m

:s. Finally, the prior of the ITG_Performance node is set by

analyzing the occurrence of each one of the possible levels pl0-pl5.

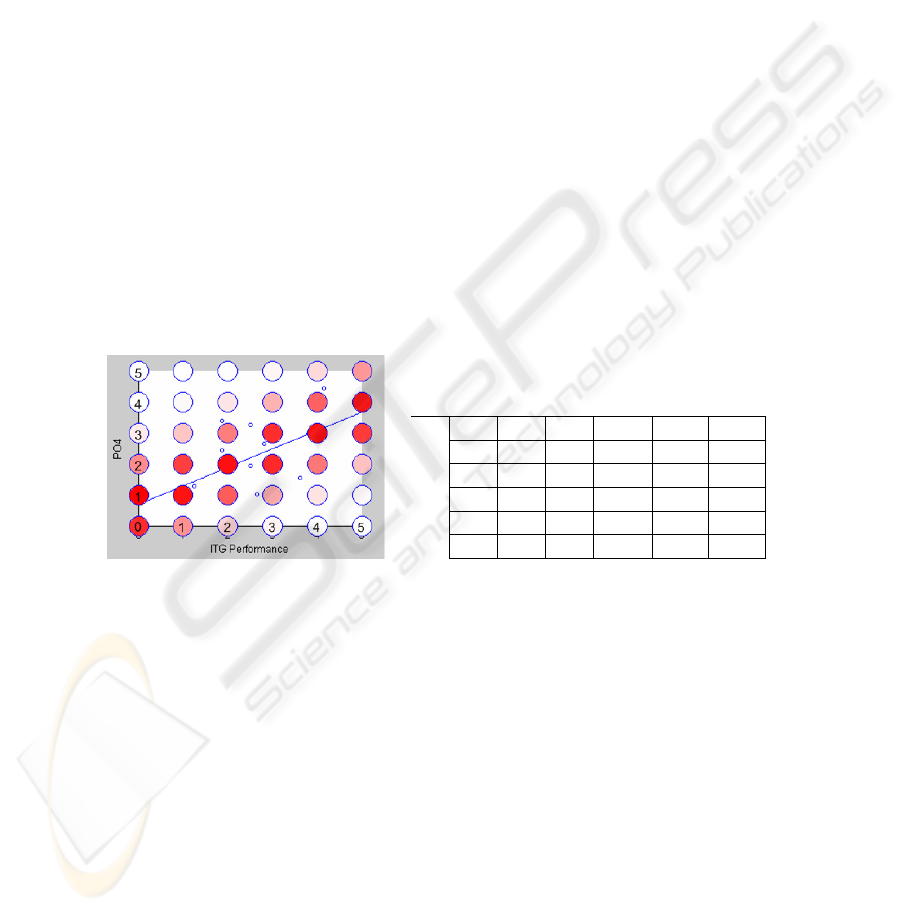
CPM for PO4 and ITG_Performance (rounded)

pl0 pl1 pl2 pl3 pl4 pl5

ml5 0,01 0,01 0,01 0,02 0,06 0,17

ml4 0,01 0,01 0,04 0,13 0,26 0,39

ml3 0,03 0,10 0,22 0,35 0,40 0,33

ml2 0,19 0,32 0,40 0,35 0,23 0,10

ml1 0,42 0,39 0,27 0,14 0,05 0,01

ml0 0,35 0,18 0,07 0,02 0,01 0,01

Fig. 4. Calculations of IT process PO4’s maturity and observations of ITG_Performance (small

dots), the linear approximation of the relation between them (ITG_Performance = 0.60*PO4 +

0.69, S = 0.96), and how these fit into the CPM (colored bubbles). The resulting CPM is shown

to the right.

S denotes the standard deviation of the residuals [1],[27]. A small S indicates a good

fit to the linear model. If only a limited amount of datasets have been used in order

for the Bayesian network to learn, all levels of ITG_Performance have perhaps not

been observed. This can be corrected for by using Laplace’s estimation, i.e. add 1 to

the number of observations assigned to each state [10]. In this way, no zeros will be

present in the resulting CPM and it is thus resulting in a better and more smoothly

predicting Bayesian network. Fig.

4 shows observations for Y = PO4 (Define the IT

processes, Organization and Relationships) and X = ITG_Performance, the linear

approximation and a graphic representation of the probability mass for each cell in

177

the CPM. The darker red the color of a bubble, the higher the probability mass P(y

)

of the corresponding cell in the CPM.

6 Discussion & Conclusions

As of March 2008, about 160 interviews have been conducted within in 35 different

organizations. The collected data spans a variety of industries, including banks, the

public sector, telecommunications, electric utilities and manufacturing. The LCPMG

has been applied upon the collected data in order for the Bayesian network for IT

Governance Performance to learn. In spite of the variety of empirical data, correla-

tions between IT governance performance and IT governance maturity indicators are

clearly visible, and the Bayesian network is already usable for making predictions.

Based on the current sets of data it seems that the maturity indicators that most

strongly correlate with IT governance performance do not differ among industries. In

summary, this paper has been discussing the use of Bayesian networks for prediction

of IT governance performance. The Linear Conditional Probability Matrix Generator,

LCPMG, is proposed as a way for Bayesian networks to learn from small datasets.

The resulting network can be employed to make well-informed decisions regarding

IT governance performance. Finally, the authors would like to thank Professor Stefan

Arnborg for his valuable input on Bayesian statistics.

References

1. Cohen, J., Cohen, P.: Applied Multiple Regression/Correlation Analysis for the Behavioral

Sciences. Lawrence Erlbaum Associates. (1983)

Debraceny, R.S.: Re-engineering IT Internal Controls - Applying Capability Maturity

Models to the Evaluation of IT Controls. Proceedings of the 39th Hawaii International

Conference on System Sciences. (2006)

Friedman, N.: The Bayesian Structural EM Algorithm. In Proceedings of the Fourteenth

Conference on Uncertainty in Artificial Intelligence (UAI '98), San Francisco, United

States. (1998)

Friedman, N., Linial, M., Nachman, I., Pe’er, D.: Using Bayesian Networks to Analyze

Expression Data. Journal of Computational Biology. 7(3-4) (2000) 601-620

Guldentops, E.: Governing Information Technology through COBIT. In: Van Grembergen, W.

(ed.): Strategies for Information Technology Governance. Idea Group Publishing (2004)

Hendersen, J.C., Venkatraman, N.: Strategic Alignment: Leveraging Information Technol-

ogy for Transforming Organizations. IBM Systems Journal, Vol. 32(1) (1993) 472-485

Holm Larsen, M., Kühn Pedersen, M., Viborg Andersen, K.: IT Governance – Reviewing

17 IT Governance Tools and Analyzing the Case of Novozymes A/S. Proceedings of the

39th Hawaii International Conference on System Sciences. (2006)

International Organization for Standardization.: ISO/IEC 20000-1 & ISO/IEC 20000-2.

(2005)

IT Governance Institute.: Control Objectives for Information and Related Technology, 4

Edition, http://www.itgi.org. (2005)

10.

IT Governance Institute.: Val IT Framework, http://www.itgi.org. (2007)

11.

Jensen, F.: Bayesian Networks and Decision Graphs. Springer-Verlag (2001)

178

12. Johnson, P., Lagerström, R., Närman, P., Simonsson, M.: Enterprise Architecture Analysis

with Extended Influence Diagrams. Information Systems Frontiers, Vol. 9, No. 2, 2007.

13.

Korac-Kakabadse, N., Kakabadse, A.: IS/IT Governance: Need For an Integrated Model.

Corporate Governance 4 (1). (2001) 9-11

14.

Lauritzen, S.: The EM Algorithm for Graphical Association Models with Missing Data.

Computational Statistics and Data Analysis, Vol. 19. (1995) 191-201.

15.

Loh, L. and N. Venkatraman.: Diffusion of Information Technology Outsourcing: Influ-

ence Sources and the Kodak Effect. Information Systems Research 3(4) (1992) 334-359.

16.

Madsen, A., Lang, M., Kjaerulff, U., Jensen, F.: The Hugin Tool for Learning Bayesian

Networks. Symbolic and Quantitative Approaches to Reasoning with Uncertainty, Vol.

2711. Springer Berlin/Heidelberg (2004) 594-605.

17.

Myllymäki, P., Silander, T., Tirri, H., Uronen, P.: B-Course: A Web-Based Tool for Bayes-

ian and Causal Data Analysis. International Journal on Artificial Intelligence Tools, Vol.

11 (2002) 369-387

18.

Neapolitan, R.: Learning Bayesian Networks. Prentice-Hall (2003)

19.

Office of Government Commerce.: IT Infrastructure Library Service Delivery. The Sta-

tionery Office (2003)

20.

Office of Government Commerce.: Service Strategy Book. The Stationery Office (2007)

21.

Pearl, J.: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference.

Morgan Kaufmann (1988)

22.

Ridley, G., Young, J., Carroll, P.: COBIT and its Utilization - A Framework from the

Literature. Proceedings of the 37th Hawaii International Conference on System Sciences,

Hawaii. (2004)

23.

Ross, J.W.: Creating a Strategic IT Architecture Competency - Learning in Stages. MIT

Sloan School of Management Working Paper No. 4314-03. (2003)

24.

Shachter, R.: Probabilistic inference and influence diagrams. Operations Research, 36(4)

(1988) 589-604

25.

Simonsson, M., Johnson, P., Wijkström, H.: Model-based IT governance maturity assess-

ments with Cobit. Proceedings of the European Conference on Information Systems.

(2007)

26.

Simonsson, M., Johnson, P.: The IT Organization Modeling and Assessment Tool: Corre-

lating IT Governance Maturity with the Effect of IT. Proceedings of the 41:st Hawaii Inter-

national Conference on System Sciences, Hawaii, United States (2008)

27.

Walsh, C.: Statistics for the Social Sciences with Computer Applications. Harper & Row

Publishers (1990)

28.

Warland, C., Ridley, G.: Awareness of IT Control Frameworks in an Australian State Gov-

ernment: A Qualitative Case Study. Proceedings of the 38th Hawaii International Confer-

ence on System Sciences, Hawaii. (2005)

29.

Weill, P., Woodham, R.: Dont Just Lead, Govern: Implementing Effective IT Governance.

MIT Sloan School of Management Working Paper No. 4237-02 (2002)

30.

Weill, P., Ross, J.: IT Governance – How Top Performers Manage IT Decision Rights for

Superior Results. Harvard Business School Press (2004).

179