
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN
Case of the Wholesale Price Contract
Omar Kallel
1,2
, Ines Ben Jaafar
1
, Lionel Dupont
2
and Khaled Ghedira
1
1
SOIE – Stratégies d’Optimisation des Informations et de la connaissancE,
ISG de Tunis Cité Bouchoucha, Bardo 2000, Tunisie
2
Ecole des Mines d’Albi-Carmaux Centre Génie Industriel
Campus Jarlard, Route de Teillet, 81013 Albi Cedex 09, France
Keywords: Multiagent systems, Automated negotiation, Contracts.
Abstract: In this paper, we propose a multi-agent negotiation model for the wholesale price contract (price: W,
quantity: Q) in a supply chain with a retailer buying from several subcontractors. We assumed that the
retailer stocks up from several subcontractors in order to face a market with fixed demand. Each
subcontractor has a normal production capacity (CN) which can be increased until a maximal capacity (CM)
but with an additional cost. The demand is superior to the sum of normal capacities and inferior to the sum
of maximal capacities. Thereby, the negotiated and agreed price between the retailer and each subcontractor
relies on the ordered quantity and the extra cost generated by any excess capacity (above the CN level).
Under asymmetric informational context, we propose a multi-agent model which is a duplication of the
considered supply chain; subcontractor agents negotiate a combination (price, quantity) in order to
maximize their benefits and a retailer agent negotiates several combinations (price, quantity) with the
different subcontractor agents in order to satisfy demand, allocate quantities and maximize its margin.
Experimental results shows that the objective of reaching agreements and establish a long-lasting “win-win”
partnership is totally reached but repartition of benefits is not so fair.
1 INTRODUCTION
In the current economic context, competition is no
more between different “stand-alone” companies but
between different groups of companies constituting
different supply chains. Founding strong links of
cooperation and synergy between companies of the
same supply chain has become a key success factor.
Therefore, companies try to establish a long-lasting
partnership between them. Those relations are
materialized by contractual engagements which are
subject of negotiations where each contracting party
tries to protect his interests in a long-lasting
relationship. Several contract types have been
investigated in the economic literature (Cachon,
2004) (Duvallet & al., 2006) (Gomez-Padilla, 2005).
These researches have focused on the impact that
these contracts may have on the performance of the
supply chain and its actors. They converge to the
point that such contractual modalities are fully
integrated into the decision-making process of
companies (Duvallet & al., 2006). Nevertheless, an
important aspect remains untreated (Cachon, 2004)
which is the negotiation of those contractual
relations. Those contracts were well studied in the
economic literature but ignored as to the negotiation
aspect. In order to investigate this important aspect,
we propose in this paper a multi-agent negotiation
system for a particular contract type which is the
wholesale price contract. With this contract, the
retailer pays the ordered quantity Q to a
subcontractor at a unitary price W.
Automated negotiation has received a significant
attention in the literature. Indeed, several approaches
have been studied (Jennings & al., 2001); game-
theoretic approaches, heuristic-based approaches,
and argumentation-based approaches. The first kind
of these approaches employs technics from game
theory in order to establish the negotiation process
and the strategies undertaken by the negotiator
agents. These negotiation technics have the
advantage and the ability of providing optimal
solutions. However, they require long and important
computation duration and capabilities. They also
assume that negotiator agents have complete
305
Kallel O., Ben Jaafar I., Dupont L. and Ghedira K. (2008).
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN - Case of the Wholesale Price Contract.
In Proceedings of the Tenth International Conference on Enterprise Information Systems, pages 305-314
DOI: 10.5220/0001737603050314
Copyright
c
SciTePress

information. The heuristic-based approach allows
overcoming the limits of the game-theoretic
approach, however, it doesn’t produce optimal
solutions but good solutions. This approach provides
more flexibility for the designer of agents; models
are based on more realistic assumptions, negotiator
agents don’t need to have complete information to
evolve in the negotiation process and the
computation requirements is pretty low. The
argumentation-based approach is based on
information exchange. Indeed, an argumentation-
based model is a negotiation process whereby agents
are allowed to send information in addition to their
offers in order to influence the counterpart.
Among these approaches, we selected and used
the heuristic-based approach for two main reasons;
first, it allows dealing with more realistic
assumptions and second, in our context, information
exchange is asymmetrical at the beginning of the
negotiation (for assumptions) and useless during the
negotiation process.
In this paper, we propose a multi-agent
negotiation model for the wholesale price contract
(price: W, quantity: Q) (Cachon, 2004) (Gomez-
Padilla, 2005) (Spengler, 1950) in a supply chain
with a retailer buying from several subcontractors.
Each subcontractor has a normal production capacity
(CN) which can be increased until a maximal
capacity (CM) with an additional cost. For the goods
produced above the CN level, each subcontractor
has an additional cost which can be low or high
according to his productive system. Therefore, the
negotiated and agreed price with the retailer should
rely on the ordered quantity and the additional cost
caused by any excess capacity. On the other side, the
retailer faces a market with fixed demand which is
superior to the sum of normal production capacities
and inferior to the sum of maximal production
capacities of the different subcontractors. He musts
allocate quantities and agree on the wholesale prices
with the subcontractors in order to maximize his
benefits.
The information exchange is asymmetrical in the
model. Public information are the fixed demand, the
selling price and capacities (normal and maximal) of
each subcontractor. Information concerning costs
calculation systems of each actor are considered as
private and not shared.
The proposed multi-agent model is a
representation of the related supply chain;
subcontractor agents negotiate a combination (price,
quantity) in order to maximize their benefits and a
retailer agent negotiates several combinations (price,
quantity) with the different subcontractor agents in
order to satisfy demand, allocate quantities and
maximize its margin.
The objective of the proposed model is to help
agents reach an agreement for a long lasting
partnership and establish a win-win relation which is
a key success factor in every supply chain. The ideal
objective is that repartition of benefits happen as fair
as possible which means that repartition occur
approximately according to the added-value of each
actor (each actor costs relatively to the global chain
costs).
The paper is organized as follows. The next
section presents related works. In section 3, we
present the mathematic modelling of the related
supply chain. Section 4 describes the multiagent
model including the architecture and the negotiation
dynamic. Section 5 outlines experimental results.
And finally, the last section contains concluding
remarks and future works.
2 RELATED WORK
Coordination by contracts is one of the main
problems in the supply chain management area. A
contract is a convention between two or several
parties ending to create between them a legal bond.
This main problem has received significant
attention. Indeed, several researches (Cachon, 2004)
(Duvallet & al., 2006) (Gomez-Padilla, 2005) have
investigated the impact that several contract types
may have on the performance of a supply chain and
its actors. Seven contract types have been studied,
proposed and applied in order to find or to assure an
efficient coordination where we maximize, at the
same time, profit of the chain and profits of the
different actors (Cachon, 2004) (Gomez-Padilla,
2005) :
The wholesale price contract which stipulates
that the unit price is defined beforehand and
does not change whatever is the ordered
quantity for the contract duration.
The quantity discount contract represents an
improved variant of the wholesale price
contract. The difference is that price is
decreasing according to the bought quantity.
The buy back contract stipulates that the
supplier or subcontractor rebuys the unsold
quantity from the retailer at a price agreed
beforehand.
The quantity flexibility contract represents a
variant of the buy back contract. In this type,
the supplier or the subcontractor rebuys the
ICEIS 2008 - International Conference on Enterprise Information Systems
306

minimum between the unsold quantity and a
percentage agreed beforehand.
The sales rebate contract stipulates that the
supplier or subcontractor grants a rebate to the
retailer for the bought units above a threshold
prefixed in the contract.
The revenue sharing contract stipulates that
the retailer pays a fixed price (relatively low)
to the supplier or the subcontractor and enlists
to pour him a percentage of sold units.
The reservation capacity contract stipulates
that the retailer reserves a capacity at the
supplier or the subcontractor. Consequently,
he pays a price per reserved unit, a price per
unit actually ordered from the reserved
capacity and a price per ordered unit in excess.
Investigated researches converge to the point that
those contractual modalities are fully integrated into
the decision-making process of companies (Duvallet
& al., 2006). Those researches (Duvallet & al.,
2006) (Gomez-Padilla, 2005) (Cachon, 2004)
essentially focused on how to identify the set of
contracts that coordinate the supply chain and
arbitrarily allocate its profit. The agreed contract is
not a subject of negotiation process. In such cases, it
seems that either the firm that offers the contract
does not matter because the aim is the supply chain
coordination. However, it is unlikely in practice that
either firm makes a single offer which is considered
as the final offer (Cachon, 2004). It is more
convenient that companies exchange several offers
and counter offers before they settle on some
agreement. The negotiation aspect of those contracts
remains untreated and additional research is surely
needed on this issue (Cachon, 2004).
Among the approaches considering supply
chains and especially negotiation in supply chains,
the multi-agents systems is an approach spilt enough
in the academic literature (Jiao & al., 2006). The
choice of such paradigm is justified by the
distributed nature of a supply chain. Indeed, every
supply chain is composed generally by autonomous,
reactive and proactive actors. Those features are the
same of an agent (Ferber, 1995). Moreover,
negotiation using multi-agent systems has received a
significant attention in the literature and several
approaches have been investigated (Jennings & al.,
2001); game-theoretic approaches, heuristic-based
approaches, and argumentation-based approaches. In
the heuristic-based approach, which is the approach
we picked out, several negotiation strategies have
been proposed. Faratin implemented (Faratin, 2000)
a multi-agent system in which agents make trade-
offs under informational uncertainty and resource
limitations context. In order to make the trade-offs,
agents employ an algorithm using the notion of
fuzzy similarity. The authors’ objective has been to
find negotiation solutions that are beneficial for both
parties. (Kraus, 2001) presented a strategic model of
negotiation where a set of agents need to reach an
agreement on a given issue. The model consists of a
protocol for the agents’ interactions, utility functions
and strategies of the agents. The utility functions
have been used to evaluate possible terminations of
the negotiation and to respond consequently. (He &
al., 2003) implemented a muti-agent system in
which autonomous agents (seller agents and buyer
agents) trade services. Those agents employ
heuristic fuzzy rules and fuzzy reasoning
mechanisms to determine the best bid to make given
the state of the marketplace. (Zhang & al., 2005)
presented a cooperative, multi-step negotiation
mechanism for task allocation. This mechanism
combines marginal utility gain and marginal utility
cost to structure the search process. It searches over
multiple attributes that reflects the concerns of both
agents in the negotiation in order to find a solution
that maximizes the agents’ combined utility. In
(Rahwan & al., 2007), the authors present a
methodology for designing agent negotiation
strategies. The authors’ aim has been to provide
some guidance for designers of strategies either in
heuristic-based or argumentation-based approaches.
In this paper, we present a negotiation model
which consists of the interaction protocol of agents
and the decision-making model of each kind of
agent. The agents use heuristics, trade-offs functions
(reduce and Increase) and utility functions (margin)
in order to reach agreements. The model differs from
the proposed negotiation models not only by the
implemented heuristics and trade-offs functions, but
also because it is studied in a particular context
which is assuring a long-lasting partnership by the
wholesale price contract. The negotiation of the
several contracts mentioned above has not been
investigated. Those contracts were well studied in
the economic literature but ignored as to the
negotiation aspect.
3 MATHEMATIC MODELLING
The model is a supply chain composed by several
subcontractors and a retailer (Figure 1). The retailer
stocks up from several subcontractors in order to
face a market with fixed demand D. Each
subcontractor has a normal production capacity
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN - Case of the Wholsale Price Contract
307
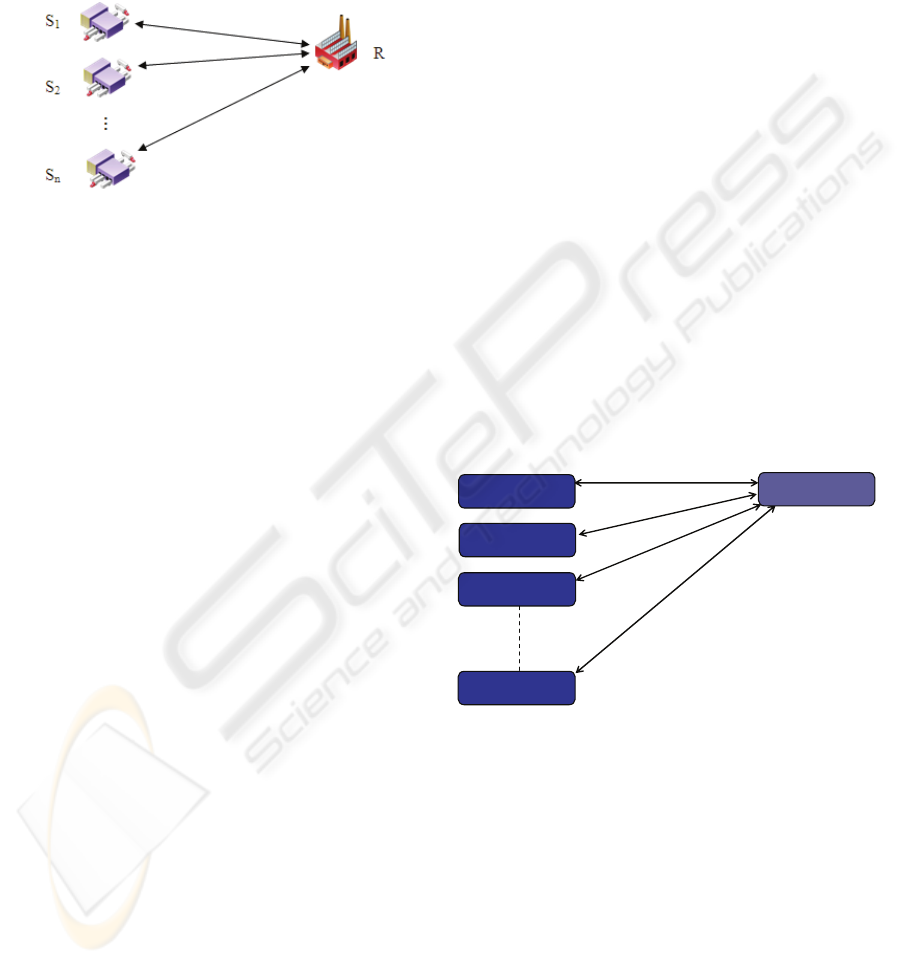
(CNi) which can be increased until a maximal
capacity (CMi) with an additional cost.
In order to satisfy the demand, the retailer order
from each subcontractor a quantity Qi (ΣQi=D) at a
unitary price Wi.
Figure 1: Considered supply chain.
3.1 Subcontractor
i
Each subcontractor has a normal production capacity
CNi. Until this capacity, he has a variable
production cost VSi. He can raise it proportionally
(overtimes, interim…) until a maximal capacity
CMi, but with a higher variable cost V2Si. In
addition to these variable costs, each subcontractor
supports fixed costs FSi.
A subcontractor’s costs CSi relies on the ordered
quantity Qi and on the normal and maximal
production capacities (CNi, CMi):
If Qi ≤ CNi Then CSi=FSi+VSi*Qi
If CNi < Qi ≤ CMi Then
CSi = FSi + VSi*CNi + V2Si*(Qi – CNi)
(2)
His profit margin MSi is as follows:
MSi = Wi*Qi- CSi (3)
3.2 Retailer
The retailer faces a market with fixed demand D.
His selling price P in the market is known. He stocks
up from several subcontractors. He supports fixed
costs FR (locals, staves ...) and variable costs per
unit VR (finishing, wrapping...).
The retailer costs CR are: fixed costs FR,
purchasing costs (financial transfers) from
subcontractors and other variable costs of production
and distribution per unit VR.
CR = FR + ∑ Wi*Qi + VR * D (4)
His profit margin MR is the difference between
his sales on the final market and his whole costs:
MR = P*D – CR
(5)
3.3 The Supply Chain Margin and
Costs
The global chain costs CCH is the sum of the
different actors’ costs:
CCH = CR + ∑ CSi
(6)
The global chain margin MCH is the sum of the
different actors’ margin:
MCH = MR + ∑ MSi
(7)
CCH and MCH are not used in the negotiation
model. They will be used in section 5 to evaluate if
the found solutions present a fair margin repartition.
4 MULTI-AGENT MODEL
Modelling supply chains with the multi-agent
paradigm has received in the last decade a
significant attention (Jiao & al., 2006). This
approach allows building autonomous entities
(agents) which are able to communicate and interact
in order to cooperate or reach an agreement.
Retailer
A
g
ent
Subcontrac tor
A
g
ent 1
Subcontrac tor
A
g
ent 2
Subcontrac tor
A
g
en
t
3
Subcontrac tor
A
g
en
t
n
Figure 2: Multi-Agent Architecture.
4.1 Multi-Agent Architecture
The model, presented in Figure2, is a duplication of
the considered supply chain. It is constituted of two
kinds of agents: Subcontractor agent (SA) and
Retailer agent (RA).
Several researches (Fiala, 2005) have
demonstrated that sharing information is generally
beneficial for both the supply chain and the actors
that compose it. Indeed, knowing the whole
information generally brings down problems to
ordinary problems or linear programs. Nevertheless,
in the real world, companies have always the
reticence to share their information principally
Σ CNi < D < Σ CMi (1)
ICEIS 2008 - International Conference on Enterprise Information Systems
308

fearing of being cheated or betrayed with
contenders. So, we have chosen to analyze the
considered model in an asymmetric informational
context. Normal CNi and maximal CMi production
capacities of each subcontractor are public.
Information concerning costs calculation systems of
each actor are considered as private and not shared.
This section presents objectives, acquaintances
(the agents that it knows) and knowledge (static and
dynamic) of each kind of agent.
4.1.1 Subcontractor Agent
Each subcontractor Agent (SAi) has the objective of
maximizing its profit margin MSi.
Its only acquaintance consists of the RA. Its
static knowledge represents information about its
productive system: its normal production capacity
CNi, its maximal production capacity CMi, its fixed
costs FSi, its variable cost for the normal capacity
VSi and its variable cost V2Si for the production
above the CNi level. Its dynamic knowledge consists
of the parameters of the negotiated contract: the
price Wi and the quantity Qi.
4.1.2 Retailer Agent
The retailer Agent (RA) has two objectives: the first
is to allocate quantities because the demand is
superior to the sum of normal production capacities
and inferior to the sum of maximal production
capacities of the different subcontractors. The
second is to maximize its profit margin MR.
The RA acquaintances consist of the set of all
SAi. Its static knowledge represents demand D, its
selling price P, its fixed costs FR, its variable costs
VR, normal and maximal production capacities of
each subcontractor (CNi, CMi). Its dynamic
knowledge consists of the states of the different SAi
during the negotiation (active, inactive, stand-by,
busy) and the parameters of the negotiated contracts:
(Wi, Qi) with the differents SAi.
4.2 Multi-Agent Dynamic
The negotiation is one-to-N multiple bilateral
negotiation. The retailer agent negotiates with
several subcontractor agents who have the same
behaviours. The negotiating process, presented in
Figure 3, is described with a UML sequence
diagram. It describes exchanged messages (FIPA
ACL Messages) between a retailer and a
subcontractor agent.
Figure 3: Negotiation process.
Before describing the dynamic, we define here
the variables used in the next procedures:
k : the k
th
iteration of the negotiation process
SAi : Subcontractor Agent number i
SAi.Q(k) : the quantity proposed in the k
th
iteration
SAi.W(k) : the price proposed in the k
th
iteration
SAi.offer(k) : the amount charged (W*Q) in the k
th
iteration
SAi.Min_turnover : the min accepted amount in the
negotiation = CSi
SAi.Begin_turnover : the amount proposed by SAi
at the start of negotiation
SAi.Hoped_turnover : the hoped amount
SAi.state : state of the SAi in the negotiation
process. Possible values are {active, inactive, stand-
by, busy}. This variable is used by RA to qualify the
evolution of each SAi in the negotiation
RA : Retailer Agent
RA.Qi(k) : the quantity proposed to SAi in the k
th
iteration
RA.Wi(k) : the price proposed to SAi in the k
th
iteration
RA.offer_i(k): the charged amount (Wi*Qi) to SAi
in the k
th
iteration
RA.offer(k): the sum of charged amounts (ΣWi*Qi)
in the k
th
iteration
RA.Min_turnover: the min accepted (global)
amount=CR
RA.Begin_turnover : the global amount (including
offers to all the SAi) proposed by RA at the start of
negotiation
RA.Hoped_turnover : the hoped (global) amount
The Begin_turnover and Hoped_turnover
influence significantly the negotiation. But those
parameters can be initiated differently according to
the business or to the commercial. In our model, we
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN - Case of the Wholsale Price Contract
309

assumed that Begin_turnover = 1.5 * Min_turnover
and Hoped_turnover = 1.2 * Min_turnover. But the
model is generic and other values can be tested. We
can even assume different values for each agent.
In addition to these variables, we use the
following function to send messages from a source
agent to a destination agent:
Send (Msg, Source, Destination)
The negotiation process is initiated by the RA. It
sends a “call for proposition” (Msg1:RA.CFP) to the
different SAi. Therefore, each SAi generates its first
offer (Msg2) with quantity equal to its maximal
capacity and price satisfying the
SAi.Begin_turnover.
Msg2: SAi.Propose (SAi.first_offer)
1. SAi.Q(0) = CMi
2. SAi.W(0) = SAi.Begin_turnover / SAi.Q(0)
3. SAi.offer(0) = SAi.W(0) * SAi.Q(0)
4. Send ( (SAi.W(0),SAi.Q(0)) , SAi , RA)
The RA collects the first offers of the different
SAi. It generates its first offers (Msg3) to the
different SAi. It allocates quantities in function of
received prices (Msg3: line 1); from the cheapest to
the most expensive. According to the allocated
quantities and to its RA.Begin_turnover, the RA
tries, while calculating prices, to minimize the
difference with those received from SAi (Msg3: line
3 to 5). Therefore, it sends offers to the SAi (Msg3:
line7).
Msg3: RA.Propose (RA.first_offer)
1. Allocate quantities on SAi
2. RA.offer(0) = RA.Begin_turnover
3. Part = ( ΣSAi.Offer(0) – RA.Offer(0) ) / D
4. For Each SAi
5. RA.Wi(0) = SAi.W(0) – Part
6. RA.offer_i(0) = RA.Wi(0) * RA.Qi(0)
7. Send ( (RA.Wi(0),RA.Qi(0)) , RA , SAi )
8. End For
A reiterated process of offer/counter-offer is set
up (Msg4, Msg5, Msg6).
If the SAi receives an offer satisfying its
SAi.Hoped_turnover, it sends its acceptance to the
RA. Also, if it receives an offer satisfying the
SAi.Min_turnover and equal to the last received
offer it sends its acceptance (Msg4: line 1, 2).
On the other hand, for each new offer, the SAi
adopts the charged quantity by the RA (Msg4:
line 4), applies a reduction to its last offer while
SAi.Min_turnover is respected (Msg4: line 5 to 10),
determines accordingly the price (Msg4: line11) and
sends its proposition to the RA (Msg4 : line 12). The
reduction is calculated according to the following
function:
ε
*
2
)(
),(
YX
YXreduce
−
=
(8)
Where:
X = The last made offer by the SAi : SAi.Offer(k)
Y = The last made offer by the RA to SAi :
RA.offer_i(k)
ε = parameter determined experimentally = 0.2
This function allows differentiating the made
reductions from iteration to another. Indeed, more
the negotiation advances more the reduction
decrease. This function contains a parameter ε which
has to be determined experimentally. This parameter
is crucial for the efficiency of the negotiation
because it determines the steps made in each
iteration; we have to avoid an efficient negotiation
process but very long-lasting and a rapid process but
inefficient. Several values have been experimented
for the parameter ε = {0.1, 0.2, 0.3 and 0.4}. The
most convenient value is 0.2.
Msg4: SAi.Propose (SAi.offer)
1. If ( RA.offer_i(k) ≥ SAi.Hoped_turnover ) OR
( ( RA.offer_i(k) = RA.offer_i(k–1) ) AND
( RA.offer_i(k) ≥ SAi.Min_turnover ) ) Then
2. Send ( Acceptance , SAi , RA )
3. Else
4. SAi.Q(k) = RA.Qi(k)
5. R = reduce( SAi.Offer(k-1) , RA.offer_i(k) )
6. If (SAi.Offer(k) – R) > SAi.Min_turnover Then
7. SAi.Offer(k) = SAi.Offer(k-1) – R
8. Else
9. SAi.Offer(k) = SAi.Offer(k-1)
10. End If
11. SAi.W(k) = SAi.Offer(k) / SAi.Q(k)
12. Send ( (SAi.W(k),SAi.Q(k)) , SAi , RA )
13. End if
The RA collects the offers of all SAi. It updates
the state of each SAi; if one of them made a
satisfying offer, then, this one is set on stand-by
(Msg6 : line 2 to 4). If it made an offer equal to its
last offer which means that it can’t evolve anymore
in the negotiation, then, it is considered as inactive
(Msg6 : line 5 to 7). After that, the RA checks the
efficiency of the quantities’ allocation(Msg6 : line
9). Then, it generates its offers to the SAi not set on
stand-by; it applies an increase to the last made
offers while RA.Min_turnover is respected (Msg6 :
line 10 to 15). The increase is calculated according
to the same principle of the subcontractor’s
reduction function but with different parameters:
ICEIS 2008 - International Conference on Enterprise Information Systems
310

ε
*
2
)(
),(
YX
YXIncrease
−
=
(9)
Where:
X = The last made offer by all the SA: ΣSAi.offer(k)
Y = The last made offer by the RA to all the SA :
RA.offer(k)
ε = parameter determined experimentally = 0.2
Prices are calculated according to the made
increase and to the assigned quantities to each SAi
(Msg6: line 16 to 18). The RA sends then its
proposition to each active SAi (Msg6 : line 20).
Msg6: RA.Propose (RA.offer)
//UPDATE STATES
1. For Each SAi
2. If SAi.Offer(k) ≤ (RA.Hoped_turnover/SAi.Q(k))
Then
3. SAi.state = stand-by
4. End If
5. If ( SAi.Offer(k) = SAi.Offer (k-1) ) Then
6. SAi.state = inactive
7. End If
8. End For
9. Check_quantities_efficiency ( )
//UPDATE OFFERS
10. I = Increase ( ΣSAi.offer(k) , RA.offer(k-1) )
11. If RA.Offer(k-1) + I ≤ RA.Min_turnover Then
12. RA.Offer(k) = RA.Offer(k-1) + I
13. Else
14. RA.Offer(k) = RA.Offer(k-1)
15. End If
16. Part = ( ΣSAi.offer(k) – RA.offer(k) ) / D
17. For Each SAi Having ( SAi.state = active )
18. RA.Wi(k) = SAi.W(k) – Part
19. RA.offer_i(k) = RA.Wi(k) * RA.Qi(k)
20. Send ( (RA.Wi(k),RA.Qi(k)) , RA , SAi )
21.
End For
With the heuristic Check_quantities_efficiency(), the
RA verifies if the quantities’ allocation made in the
last iteration is efficient. Indeed, reducing the
ordered quantity to a subcontractor agent can have
as effect a big rise of the charged price from the
latter (line3:
SAi.W(k) > β*SAi.W(k–1) ). A big rise of
price can be regarded differently according to the
business or to the commercial. β is a generic
parameter which can be generated appropriately
according to the context. In our experiments, β=1.4 .
If reducing the ordered quantity to a SA has
produced a big rise of the charged price from the
latter, the RA reviews its quantities’ allocation; it
cancels the made reduction of quantity to this
subcontractor agent and makes it to other active or in
stand-by subcontractor agent in function of prices
from the most expensive to the cheapest (line 8 to
26).
Check_quantities_efficiency ( )
Qa : the quantity to reapportion
1. Qa = 0
2. For Each SAi Having ( SAi.state = active )
3. If ( SAi.W(k) > β*SAi.W(k–1) ) Then
4. RA.Qi(k) = RA.Qi(k-1)
5. Qa = Qa + (RA.Qi(k-1) – RA.Qi(k))
6. SAi.state = busy
// reducing Qa from other active or in stand-by SA in
function of prices from the most expensive to the cheapest
7. While (Qa > 0)
8. max_w = 0 , indmax = -1
9. For Each SAj Having ( SAj.state = active )
10. If (max_w < SAj.w(k)) Then
11. max_w = SAj.w(k)
12. indmax = j
13. End if
14. End For
15. If (indmax = -1) Then
16. For Each SAj Having (SAj.state=stand-by)
17. If (max_w < SAj.w(k)) Then
18. max_w = SAj.w(k)
19. indmax = j
20. End if
21. End For
22. SAj.state = active
23. End If
24. If (indmax <> -1) Then
25. RA.Qj(k) = RA.Qj(k) – Qa
26. End If
27. End While
28. End If
29. End For
30. For Each SAi Having ( SAi.state = busy )
31. SAi.state = active
32. End For
The reiterated process of offer/counter-offer is
engaged till the RA terminates the negotiation either
by sending “success” or “fail” to each SAi involved
in the negotiation (Msg7:RA.Inform(Success/Fail)).
When the state of each SAi is either stand-by or
inactive and an agreement is reached with at least
some SAi able to respond to the demand D, the RA
stops the negotiation and informs the counterparts of
“success” of the negotiation. When a number of
maximal iterations is reached without attaining an
agreement, the RA stops the negotiation and informs
the counterparts of the “fail”.
5 EXPERIMENTS
We have implemented this model with JADE
platform (Bellifemine & al., 2007) which is one of
the most known MAS platforms.
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN - Case of the Wholsale Price Contract
311

Table 1: Experimental Results
Assumptions Margin Contracts
R P=80 D=500 FR=10000 VR=15 10924.969 C1 to C2
Case1 S1 CN=350 CM=420 FS=4000 VS=10 V2S=13 541.249 C1 (22.974, 350)
S2 CN=100 CM=150 FS=1500 VS=12 V2S=14 133.780 C2 (23.558, 150)
R P= 5 D=1000 F R=1000 VR= 1 528.907 C1 to C2
Case2 S1 CN=500 CM=550 FS=1000 VS=0.5 V2S=0.9 38.357 C1 (2.424, 550)
S2 CN=400 CM=500 FS=800 VS=0.7 V2S=1 7.735 C2 (2.528, 450)
R P= 3 D=10000 FR= 5000 VR=0.3 4469. 648 C1 to C3
Case3 S1 CN=2000 CM=2400 FS=2000 VS=1 V2S=1.2 70.359 C1 (2.035, 2000)
S2 CN=4000 CM=4300 FS=4000 VS=0.6 V2S=1.1 549.893 C2 (1.692, 4300)
S3 CN=3500 CM=3700 FS=3500 VS=0.7 V2S=1.1 10.099 C3 (1.67 , 3700)
R P= 40 D=500 F R=3000 VR=8 3551.001 C1 to C3
Case4 S1 CN=150 CM=190 FS=1600 VS=6 V2S=7.5 329.275 C1 (18.861, 150)
S2 CN=220 CM=250 FS=2000 VS=5 V2S=7 1369.716 C2 (18.718, 250)
S3 CN=80 CM=100 FS=1200 VS=7 V2S=7.8 24.006 C3 (19.4 , 100)
R P=15 D=3000 FR=4000 VR=3 4193.881 C1 to C4
S1 CN=800 CM=850 FS=4000 VS=4 V2S=5.5 175.882 C1 (9.001 , 850)
Case5 S2 CN=850 CM=870 FS=5000 VS=3.5 V2S=5 347.626 C2 (10.444, 770)
S3 CN=700 CM=800 FS=3000 VS=4.5 V2S=6.2 32.889 C3 (8.503 , 800)
S4 CN=500 CM=580 FS=2000 VS=5.2 V2S=7 149.719 C4 (9.154 , 580)
R P= 24 D=860 F R=750 VR=5 3805.19 C1 to C4
S1 CN=230 CM=260 FS=850 VS=8 V2S=9.2 578.726 C1 (13.633, 260)
Case6 S2 CN=340 CM=350 FS=110 VS=7 V2S=8 1267.429 C2 (13.792, 350)
S3 CN=160 CM=200 FS=700 VS=8.5 V2S=9.5 37.807 C3 (13.111, 160)
S4 CN=70 CM=90 FS=450 VS=9 V2S=10.5 24.845 C4 (14.609, 90)
R P=20 D=1200 FR=2400 VR=4 2292.64 C1 to C4
S1 CN=380 CM=410 FS=700 VS=9 V2S=10.5 136.443 C1 (11.149, 410)
Case7 S2 CN=300 CM=350 FS=600 VS=9.5 V2S=11 53.5393 C2 (11.581, 350)
S3 CN=250 CM=350 FS=500 VS=10 V2S=11 272.231 C3 (13.217, 240)
S4 CN=150 CM=200 FS=350 VS =11 V2S= 12 110.290 C4 (13. 551, 200)
R P=30 D=1000 FR=800 VR=6 5509.687 C1 to C5
S1 CN=200 CM=230 FS=1000 VS=10 V2S=12 666.035 C1 (17.504, 230)
Case8 S2 CN=370 CM=380 FS=1500 VS=9 V2S=10.5 1780.564 C2 (17.672, 380)
S3 CN=150 CM=200 FS=900 VS=11 V2S=12 169.872 C3 (18.132, 150)
S4 CN=100 CM=150 FS=500 VS=11.5 V2S=13 359.962 C4 (17.733, 150)
S5 CN=80 CM=90 FS=300 VS=12.5 V2S=14 128.878 C5 (17.431, 90)
R P=15 D=1080 FR=500 VR=3 3585.035 C1 to C5
S1 CN=250 CM=280 FS=700 VS=5 V2S=6.5 2.899 C1 (7.671, 280)
Case9 S2 CN=200 CM=220 FS=600 VS=5.3 V2S=6 39.157 C2 (9.059, 170)
S3 CN=300 CM=310 FS=900 VS=4.5 V2S=5 104.657 C3 (7.756, 310)
S4 CN=110 CM=145 FS=500 VS=5.8 V2S=6.5 51.727 C4 (9.773, 145)
S5 CN=120 CM=145 FS=470 VS=6 V2S=6.6 10.022 C5 (9.413, 145)
R P=22 D=5000 FR=12000 VR=7 5407.145 C1 to C5
S1 CN=1200 CM=1250 FS=8000 VS=4 V2S=6 438.674 C1 (10.83 , 1250)
Case10 S2 CN=900 CM=1000 FS=6000 VS=5 V2S=6.5 476.361 C2 (13.635, 750)
S3 CN=1000 CM=1150 FS=7000 VS=4.5 V2S=6.2 592.58 C3 (11.323, 1150)
S4 CN=600 CM=680 FS=3500 VS=5.5 V2S=7 355.438 C4 (11.346, 680)
S5 CN=1100 CM=1170 FS=7500 VS=4.2 V2S=6 549.799 C5 (11.187, 1170)
The implemented model differs from the iterated
contract net protocol (FIPA, 2002) because a Call
for propositions is sent only at the beginning and
there is no limitation of time to respond in each
iteration but there is a limitation in the number of
maximal iterations. Moreover, the RA can qualify its
contenders with states and acts with each SAi in the
negotiation according to its state which is not the
case in the iterated contract net protocol. For
example, the RA can put a SAi into a standby state
in some iterations and then reinstate it in the
negotiation process.
The experiments done allowed us to verify if the
proposed model can lead agents to reach an
agreement. Table1 presents some examples of our
experiments. These examples approach real
ICEIS 2008 - International Conference on Enterprise Information Systems
312
industrial cases. We assumed that different
subcontractors’ profiles exist: those who have
invested to automate their work process and
consequently have high fixed costs and relatively
low variable costs, and those who didn’t invest and
consequently have low fixed costs and relatively
high variable costs. In the case 1, we took as
assumptions a retailer negotiating with 2
subcontractors. The retailer respond to a fixed
demand D=500, his selling price P is 80, he supports
fixed costs FR=10000 and variable costs per unit
VR=15. The first subcontractor S1 has a normal
capacity CN=350, a maximal capacity CM=420,
fixed costs FS=4000, variable cost for the normal
capacity VS=10 and variable cost V2S=13 for the
production in excess (above the CN level). The
second subcontractor S2 has a normal capacity
CN=100, a maximal capacity CM=50, fixed costs
FS=1500, variable cost for the normal capacity
VS=12 and variable cost V2S=14 for the production
in excess. After simulation, the agreed contracts
were: C1(22.974, 350) and C2(23.558, 150).
The implementation of this model has been made
in two phases. First, we noticed that agreements can
be reached but sometimes with illogical prices. In
the case 1, agreed contracts were: C1(22.926, 420)
and C2(37.487,80). As noticed, it’s illogic to
negotiate, for the same product, price around 22 with
the first SA and around 37 with the second SA. Such
illogical prices are generated when the quantity
charged by the RA to a SA is relatively low. Thus,
we added the heuristic Check_quantity_efficiency()
in the decision-making process of the RA. This
heuristic allows the RA to verify if the quantities’
allocation made in the last iteration is efficient and
to review it if necessary. Experiments have
demonstrated that there are no more illogical
negotiated prices. With the heuristic
Check_quantity_efficiency(), agreed contracts in the
case 1 were : C1(22.974, 350) and C2(23.558, 150).
Among the experiments done, we found some
cases where results are the same with the two
models. In such cases, the quantities’ allocation had
no big impact on prices (Table1: Cases2, 3, 5, 10).
But, for many other examples, as those presented in
Figure4, the quantities’ allocation has produced a
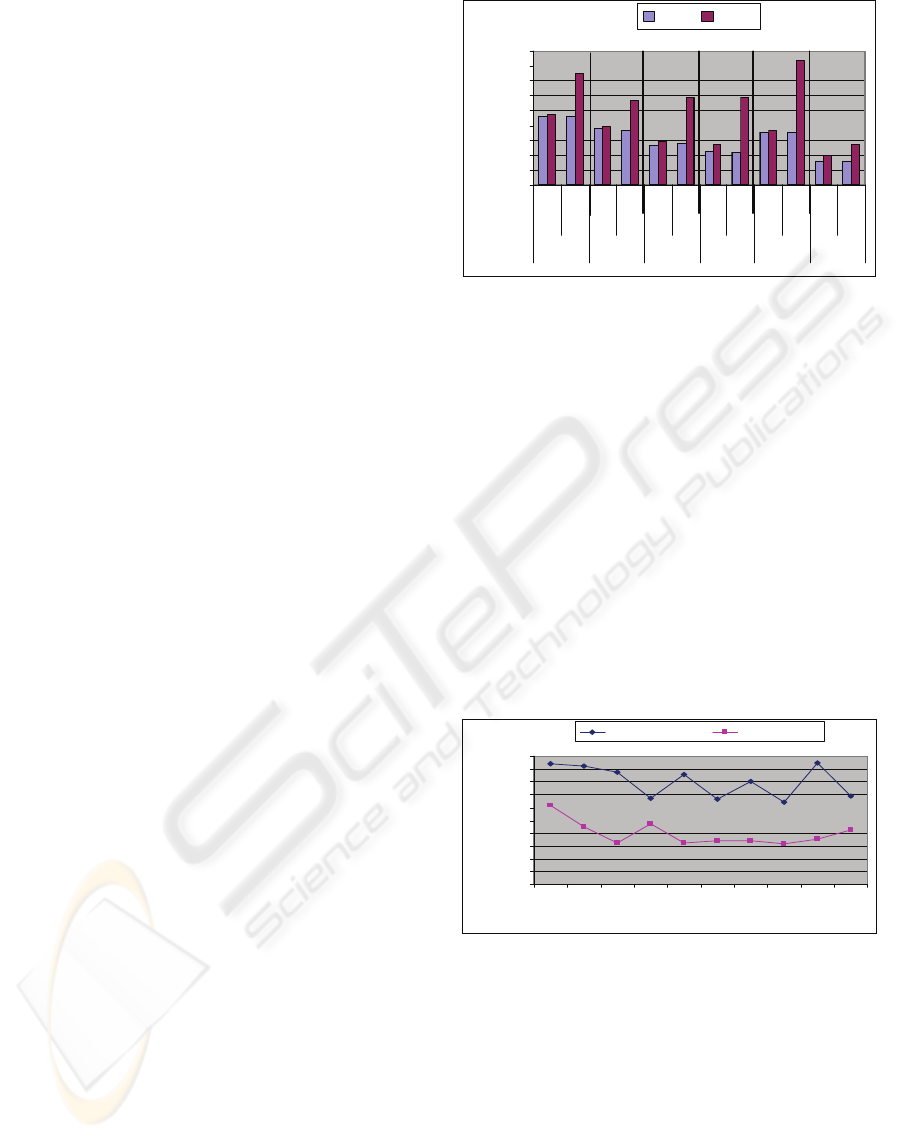
big rise in at least one of the negotiated prices.
Figure 4 presents the min and the max prices
agreed for each model. We notice that without the
heuristic Check_quantity_efficiency(), the difference
between the min and the max agreed prices is huge
which is illogic. Nevertheless, using
Check_quantity_efficiency() allows the RA to
negotiate quite prices which is more realistic.
0
5
10
15
20
25
30
35
40
45
with
without
with
without
with
without
with
without
with
without
with
without
Case1 Case4 Case6 Case7 Case8 Case9
P
r
i
c
e
Min Max
Figure 4: Comparison with/without
Check_quantity_efficiency( ).
The objective of the proposed model is to help
agents reach agreements for a long lasting
partnership and establish a win-win relation which is
a key success factor in every supply chain. This
objective has been largely reached. But, the ideal
objective is that repartition of benefits happen as fair
as possible which means that margin’s repartition
has to occur according to the costs of each actor
relatively to the chain costs. Figure 5 presents a fair
repartition and the results we found (Model
repartition). We conclude that agents certainly reach
an agreement to establish a win-win long lasting
partnership but the repartition is not so fair. Agents
have to be more cooperative to reach more equitable
repartition of benefits.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
2233444555
Number of Subcontractors
Retailer Margin /
Chain Margin (%
)
Model repartition fair repartition
Figure 5: Comparison fair repartition (CR/CCH) –Model
repartition (MR/MCH).
6 CONCLUSIONS AND FUTURE
WORKS
In this work, we focused on a supply chain
constituted by several subcontractors and a retailer
in a particular contractual context which is the
wholesale price contract (Price: W, Quantity: Q).We
assumed that the retailer stocks up from several
MULTI-AGENT NEGOTIATION IN A SUPPLY CHAIN - Case of the Wholsale Price Contract
313

subcontractors in order to face a market with fixed
demand. Each subcontractor has a normal
production capacity (CN) which can be increased
until a maximal capacity (CM) but with an
additional cost. However, the demand is superior to
the sum of normal capacities and inferior to the sum
of maximal capacities. Thereby, the negotiated and
agreed price between the retailer and each
subcontractor relies on the ordered quantity and the
extra cost generated by any excess capacity (above
the CN level). The objective of the proposed model
is to help actors in an asymmetric informational
context to reach agreements for a long lasting
partnership via the wholesale price contract and
establish a win-win relation which is a key success
factor in every supply chain. The ideal objective is
that repartition of benefits happen as fair as possible
which means that it occurs approximately according
to the added-value of each actor (each actor costs
relatively to the global chain costs).
To handle this problem, we have chosen the
multi-agent approach. The model is a representation
of the related supply chain; subcontractor agents
negotiate a combination (price, quantity) in order to
maximize their benefits and a retailer agent
negotiates several combinations (price, quantity)
with the different subcontractor agents in order to
satisfy demand, allocate quantities and maximize its
margin. The model has been implemented in two
phases. First, we have found that agreements are
reached but sometimes with illogical prices. Then,
we added the check_quantity_efficiency() in the
decision-making process of the RA. This heuristic
allows the RA to verify if the quantities’ allocation
is efficient and to review it if necessary. Since, we
found agreements with logical prices.
Experiments have demonstrated that agreements
are possible. The objective of assuring a long-lasting
partnership via the wholesale price contract is
largely reached and a win-win relation can be
established. However, the ideal objective of making
the repartition as fair as possible is not totally
reached and more investigation has to be done.
This research has several perspectives. First, we
intend to extend the proposed model by making
agents more cooperative in order to reach a more fair
repartition of benefits under incomplete
informational context. This can be done by
integrating learning technics in agents or by treating
the problem as a multicriteria problem. Second, we
plan to treat the model with a stochastic demand.
And finally, we intend to propose a negotiation
model combining several contract types.
REFERENCES
Bellifemine, F., Caire, G. and Greenwood., D., 2007.
"Developing Multi-Agent Systems with JADE". John
Wiley & Sons, Chichester, UK.
Cachon, G.P., 2004. "Supply Chain Coordination with
Contracts", In S. Graves & T. de Kok (Eds.),
Handbooks in Operations Research and Management
Science. North Holland Press.
Duvallet, J., Gomez-Padilla, A., LLERENA, D., 2006.
"Approche économique de la coordination dans les
chaînes logistiques". MOSIM’06. Rabat, Maroc.
Faratin, P., 2000. "Automated service negotiation between
autonomous computational agents". Ph.D. thesis,
University of London, Queen Mary and Westfield
College, Department of Electronic Engineering.
Ferber, J., 1995. "Les Systèmes Multi-Agents, vers une
intelligence collective". InterEdition. Paris.
Fiala, P., 2005. "Information sharing in supply chains".
Omega, Volume 33, Issue 5, Pages 419-423.
FIPA, 2002. "FIPA Iterated Contract Net Interaction
Protocol Specification", Foundation for Intelligent
physical agents,http://www.fipa.org/specs/fipa00030/
Gomez-Padilla, A., 2005. "Modélisation des relations
verticales : une approche économique et logistique".
PhD Thesis. I.N.P. de Grenoble. September 2005.
He, M., Leung, H., Jennings, N. R., 2003. "A fuzzy logic
based bidding strategy for autonomous agents in
continuous double auctions". IEEE Transaction on
Knowledge and Data Engineering 15(6):1345–1363.
Jennings, N., Faratin, P., Lomuscio, A., Parsons, S.,
Sierra, C., Wooldridge, M., 2001. "Automated
negotiation: Prospects, methods and challenges".
International Journal of Group Decision and
Negotiation 10, 199–215.
Jiao, J., You, X., Kumar, A., 2006. "An agent-based
framework for collaborative negotiation in the global
manufacturing Supply Chain network", Robotics and
Computer-Integrated Manufacturing, Volume 22,
Issue 3, Pages 239-255.
Kraus, S. 2001. "Strategic Negotiation in Multi-Agent
Environments". Cambridge, MA: MIT Press.
Rahwan, I., Sonenburg, L., Jennings, N. R. and
McBurney, P., 2007. "Stratum: A methodology for
designing heuristic agent negotiation strategies".
International Journal of Applied Artificial Intelligence,
21 (6). pp. 489-527.
Spengler, J., 1950. "Vertical integration and antitrust
policy". Journal of Political Economy. 347-52.
Zhang, X., Lesser, V., and Podorozhny., R., 2005.
"Multidimensional, multistep negotiation for task
allocation in a cooperative system". Autonomous
Agents and Multi-Agent Systems, Vol. 10, No. 1, pp.
5-40.
ICEIS 2008 - International Conference on Enterprise Information Systems
314
