
The Role of Attention in Understanding Spatial
Expressions under the Distractor Condition
Tatsumi Kobayashi
1
, Asuka Terai
2
and Takenobu Tokunaga
1
1
Department of Computer Science, Tokyo Institute of Technology
Tokyo Meguro
ˆ
Ookayama 2-12-1, 152-8552 Japan
2
Global Edge Institute, Tokyo Institute of Technology
Tokyo Meguro
ˆ
Ookayama 2-12-1, 152-8552 Japan
Abstract. To develop a computational model of understanding spatial expres-
sions, various factors should be taken into account. We have been exploring the
relations between the goodness-of-fit of spatial terms and various geometric fac-
tors such as the object’s size, the distance between objects and the observers’
viewpoint. Although the dual-object relation between the located and reference
objects can be handled with relatively simple models, introducing a distractor
object requires a model considering further factors to explain relations, such
as attention to the objects. Based on our experiment using Japanese topologi-
cal and projective terms, this paper proposes a computational model to estimate
the goodness-of-fit of spatial terms which incorporates an attention model for a
distractor object. The proposed model was evaluated by using our experimental
data.
1 Introduction
Elucidating the human’s cognitive mechanism of understanding spatial expressions is
important not only for cognitive science and linguistics but also engineering, in which
broad applications are expected in fields such as human-robot interaction. There have
been numerous attempts to tackle this problem by proposing computational models and
by conducting psychological experiments. Most of them, however, estimate goodness-
of-fit functions of spatial terms in limited combinations of static visual configurations
and language expressions. Analyzing the nature of each spatial term at a perceptual level
with limited conditions would be a good starting point. In fact, effective methods using
a spatial template to represent the range of spatial terms have been established [1, 2],
and several computational models have also been proposed [3–6]. However, to realise
applications for complex real world problems, the study of spatial cognition still needs
more progress.
To tackle realistic spatial cognition problems, many issues should be solved. For
instance, in a dialogue involving spatial relations, differences of visual information
and knowledge between dialogue participants must be considered. The dialogue his-
tory should be taken into account as well. The computational model would also have
to cover the diversity and complexity of geometric factors in the environment. When
Kobayashi T., Terai A. and Tokunaga T. (2008).
The Role of Attention in Understanding Spatial Expressions under the Distractor Condition.
In Proceedings of the 5th International Workshop on Natural Language Processing and Cognitive Science, pages 74-83
DOI: 10.5220/0001738200740083
Copyright
c
SciTePress

considering the functional factors between objects [7], the dialogue topic, participants’
intentions and plans, common sense and domain knowledge would be necessary. Ob-
viously there are many situations which we would be unable to resolve solely by com-
piling individual computational models of spatial terms. If we were to tackle all issues
at the same time without an appropriate research strategy, the goal to build a realistic
computational model would be unachievable. In order to get a step further toward com-
putational models of spatial terms which are applicable to the real world, we focus on
exploring the following problems [8,9].
Problem 1. Although the computational models in the past research include several
parameters for fitting real data, criteria to decide the appropriate values for those pa-
rameters are not always clear. Through our experiments, we found some of the clues
that can be used to adjust the parameters.
Problem 2. Most of the past computational models dealt with a simple configuration
consisting of two objects: a located object and a reference object. Several studies have
also pointed out that a distractor object changes the goodness-of-fit of projective terms
(e.g. left) and topological terms (e.g. near) [10–12]. We found that the effect of a dis-
tractor object depends on certain geometric factors in the visual presentation.
Problem 3. Kelleher and Kruijff [13] pointed out the difference of cognitive load be-
tween topological terms and projective terms. That is, cognitive load of understanding
topological terms is less than that of projective terms, since projective terms require set-
ting an appropriate reference frame for its interpretation. Thus, they claimed that topo-
logical terms are more preferable than projective terms. However, our intuition says
that such a simple solution could not always be accepted in reality, that is, depending
on the combination of geometric factors, left may be dominant in some situations, and
near may be dominant in others. Regarding this cognitive load issue, we analysed the
goodness-of-fit of spatial terms in variation of geometric factors.
This paper proposes an extension of an existing computational model estimating the
goodness-of-fit of spatial terms. The proposed model is based on our findings from the
experiments which were conducted to explore the nature of spatial terms corresponding
to specific attention patterns in the visual scene. Especially, it focuses on modeling
of the distractor object’s effect for the Japanese topological terms tikai (near) and t
ˆ
oi
(far from) and the projective term hidari (left). In the following sections, we firstly
explain our previous experiments, and then point out the importance of attention in the
computational model of spatial terms. Subsequently, incorporating the attention factor,
we propose a new model. Then we give a general discussion before concluding the
paper and looking at the future work.
2 Finding a Bridge to the World
We conducted experiments to investigatethe effect of a distractor object on the goodness-
of-fit of spatial terms relating two objects: a reference object and a located object [8].
75

06121824303642
LO (red)
DO (blue) RO (green)
l
1
l
2
l
3
d
1
d
2
d
3
d
4
d
1
∼d
4
: absolute position of DO
l
1
∼ l
3
: absolute position of LO
relative position of DO
Fig.1. An arrangement of in the experiment (LO at l
3
, DO at d
2
and large LO).
2.1 Experiments with Japanese Spatial Terms
In the experiments, subjects were sequentially presented 3-D CG pictures together with
sentences describing the relationship between the objects in the picture. The spatial
terms used for the experiment were two Japanese topological terms: tikai (near) and t
ˆ
oi
(far from) and one Japanese projectiveterm: hidari (left). One of the following Japanese
sentences was displayed above each picture.
“Akai b
ˆ
oru ha midori no b
ˆ
oru
no tika-ku ni
kara t
ˆ
o-ku ni
no hidari ni
arimasu”
In English, they mean “The red ball is {near / far from / to the left of } the green
ball.” As shown in Fig. 1, the picture shows three objects: the located object (LO), the
distractor object (DO) and the reference object (RO). They are arranged on the same
line with the RO being fixed at the origin. Both the RO and DO are medium-size balls
(diameter 4), and the LO is one of three sizes: small, medium and large. The colours
of the LO, DO and RO are red, blue and green respectively. We have three conditions
of the LO position (l
1
, l
2
and l
3
), three conditions of the LO size (diameters: 2, 4 and
8), five conditions of the DO position (position at d
1
, d
2
, d
3
, d
4
and no distractor case)
and three conditions of spatial terms (tikai (near), t
ˆ
oi (far from) and hidari (left)). This
makes the total of 135 stimuli (= 3 × 3 × 5 × 3), which were presented randomly to the
subjects on a computer display. Subjects were asked to provide a rating on how well the
sentence described the relationship between the LO and RO by selecting one of nine
buttons from 1 (not relevant) to 9 (most relevant).
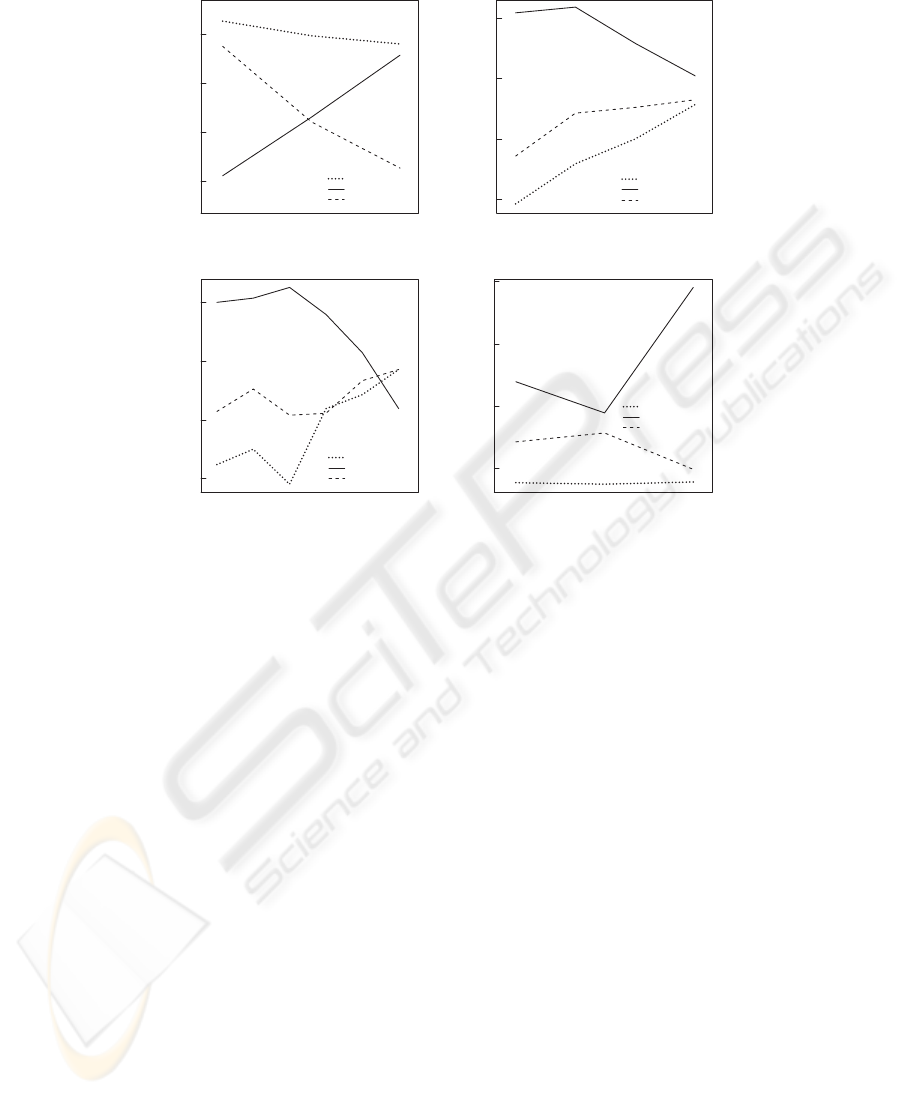
The ANOVA results of the experiment are shown in Fig. 2; (a) shows the subjects’
mean ratings of each spatial term without DO; (b) shows the interaction between the
spatial terms and the DO’s absolute position from the RO (p < .001); (c) shows the
interaction between the spatial terms and the DO’s relative position from the LO (p <
.001); (d) shows the interaction between the spatial terms and the LO size (p < .001).
In (b), (c) and (d), the vertical axis represents the mean difference of ratings between
with DO and without DO conditions of the same subject. In addition, the analysis of
each mean rating of 135 stimuli simply indicated that hidari (left) was highest-rated at
the l
1
and l
2
positions of the LO, and t
ˆ
oi (far from) at the l
3
position of the LO. Tikai
(near) was second highest-rated at the position l
2
of the LO. Detailed observations are
as follow:
76
hidari (left)
tôi (far from)
tikai (near)
Mean rating
8
6
4
2
12 24 36
LO position
(a)
Mean difference of rating
between w/ DO and w/o DO
0.5
0.0
-0.5
-1.0
DO absolute position
6 18 30 42
hidari (left)
tôi (far from)
tikai (near)
(b)
Mean difference of rating
between w/ DO and w/o DO
0.5
0.0
-0.5
-1.0
-30 -18 -6 6 18 30
DO relative position
hidari (left)
tôi (far from)
tikai (near)
(c)
Mean difference of rating
between w/ DO and w/o DO
1.0
0.5
0.0
-0.5
2 4 8
LO size
hidari (left)
tôi (far from)
tikai (near)
(d)
Fig.2. Results of ANOVA on Japanese spatial terms.
1. In the case of t
ˆ
oi (far from), the subjects’ rating shows its peak at the leftmost posi-
tion, and decreases linearly to the region near the RO. In other words, the subjects’
attention is on the region between the RO and the left boundary of the picture.
2. Tikai (near) indicates almost the opposite tendency of t
ˆ
oi (far from). Its rating de-
creases linearly, gradually going apart from the RO. It turns out that the left bound-
ary is used as a kind of reference object in terms of nearness.
3. In the case of hidari (left), the subjects’ rating decreases as they gradually goes
apart from the RO, however, the left boundary is not considered as a reference
object.
One conclusion is that the computational model must take into account the boundary
(i.e. the leftmost position in this case) for tikai (near) and t
ˆ
oi (far from), even though
it is not explicitly stated in the linguistic expressions. Regarding the aforementioned
Problem 1, it suggests the possibility to utilise the boundary as information to fit the
model to the visual scene. In addition, some properties listed below in respect to the
DO’s effect were found. Here, F
n
(n = 1 ∼ 4) are properties of t
ˆ
oi (far from), N
n
(n = 1 ∼ 3) are properties of tikai (near), and L
n
(n = 1 ∼ 3) are properties of hidari
(left).
(F
1
) The closer the DO is to the RO, the better the rating.
77

(F
2
) When the DO is located between the LO and RO, the rating im-
proves.
(F
3
) When the LO is larger than the DO, the rating improves.
(F
4
) When the DO is located far side of the LO from the RO, the rating
decreases.
(N
1
), (L
1
) The closer the DO is to the RO, the rating decreases.
(N
2
), (L
2
) When the DO locates between the LO and RO, the rating decreases.
(N
3
) When the LO is larger than the DO, the rating decreases.
(L
3
) The size of the LO has little influence on the effect by the DO.
These properties summarise tendencies of the DO’s effect for each spatial term,
which could provide a partial solution to the Problem 2 raised in section 1. At the same
time, it suggests circumstances which cannot be solved simply by using the prioritised
list of spatial terms considering the human cognitiveload as suggested in the Problem 3.
2.2 Comparison with the Relative Proximity Model
We confirmed in [9] that our experimental results of tikai (near), described in the previ-
ous section, could not be explained by Kelleher’s Relative Proximity Model (RPM) [11]
for the English spatial term near. We briefly provide the verification result and what we
learned from it. The RPM calculates P
rel
(L, x), the goodness-of-fit (relative proxim-
ity value in the Kelleher’s original paper) of the object L at position x by subtract-
ing the highest absolute proximity value given by the other object at position x, from
P
abs
(L, x), the absolute proximity value of the object L as shown in equation (3).
P
abs
(L, x) = (1 − dis t
norm
(L, x))S(L) (1)
S(L) =
S
vis
(L) + S
disc
(L)
2
(2)
P
rel
(L, x) = P
abs
(L, x) − max
∀L
n
6=L
P (L
n
, x) (3)
P
abs
(L, x) is adjusted by the salience parameter consisting of visual salience S
vis
(L)
and discourse salience S
disc
(L), and dist
norm
(L, x) is the normalised distance to the
position x from the object L.
Table 1 shows the comparison between the subjects’ rating in our experiment and
the results computed by the RPM in the case that the DO position is 18 and the LO
size is small (diameter = 2). The RO’s absolute proximity (a) is the subjects’ mean
rating without the DO in our experiment, and the RO’s relative proximity (d) is the
Table 1. Comparison between our experiment and the RPM (DO position=18, LO size=small).
LO’s
position
(a) LO abs prox
w/o DO (Exp)
(b) DO abs prox
w/o DO (RPM)
(c) LO rel prox
(a)-(b) (RPM)
(d) LO rel prox
w/ DO (Exp)
(e) DO abs prox
(a)-(d) (Exp)
12 6.929 7.0 -0.071 6.286 0.643
24 3.857 7.667 -3.810 3.429 0.428
36 2.214 5.0 -2.786 2.0 0.214
78

subject’s mean rating with the DO. The DO’s absolute proximity (b) is calculated by
linear interpolation assuming that the DO position 18 has rating 9 and the both ends of
the picture have rating 1. The linearity of the goodness-of-fit for near was confirmed
from the data as shown in Fig. 2 (a). In the experiment, since the RO and DO were
the same size, the salience parameter S(L) was set to 1. Based on these conditions and
the assumption that the values in column (a) minus the values in column (b) equal to
the values of the RPM’s equation (3), we calculated the relative proximity of the RO
(column (c)) at positions 12, 24 and 36. For comparison, we also calculated the values
of column (a) minus column (d) by considering the subjects’ ratings as the DO’s effect
(column (e)).
It is obvious that the values in column (c) computed by the RPM is quite differ-
ent from the experimental result (column (d)). The DO’s absolute proximity based on
the RPM (column (b)) is ten times bigger than the DO’s effect of the experiment (col-
umn (e)). We think that assuming the same salience parameters for both the RO and DO
causes the same result as that for Kelleher et al. [11]. Since the LO’s relative proximity
is relatively high as shown in column (d), the DO’s salience should be extremely low ac-
cording to the equation (1). We presume the problem here to be the use of the DO’s size
(= 1) directly for the DO’s salience parameter S
vis
(L), meaning equation (2) should
be reconsidered. In addition, our experiment results suggest the need for considering
attention on specific parts of space when modeling the computational model of spatial
terms considering the DO.
3 Attention-based Computational Model with a Distractor Object
Based on our experiment,we introduce a computationalmodel estimating the goodness-
of-fit of spatial terms with a distractor object, and evaluate it with our experimental data.
3.1 A Computational Model
We propose a model r
TOTAL
representing the spatial term’s goodness-of-fit by the sum
of the dual-object relation model r
LO
and the DO’s effect r
DO
. Here, x
LO
is the distance
between the RO and LO, and x
DO
is the distance between the RO and DO. We normalise
the distance between the RO and the end point (the boundary) of the scene to 1.
r
TOTAL
= r
LO
+ r
DO
(4)
r
LO
= px
LO
+ θ
LO
s
LO
+ C
LO
(5)
r
DO
= θ
DO
s
DO
(f
o
f
p
+ f
a
) + C
DO
(6)
r
LO
consists of the LO’s positions effect px
LO
, the LO’s size effect θ
LO
s
LO
and the
constant C
LO
. θ
LO
is the LO’s salience parameter which adjusts the ratio of the LO
size to the RO size, s
LO
. r
DO
consists of an attention distribution f
o
in the vicinity of
the DO, a monotonic attention distribution f
p
over the area from the RO to the farthest
point, an asymmetric attention distribution f
a
of both sides of the DO, the DO size’s
effect θ
DO
s
DO
and a constant C
DO
. θ
DO
is the DO’s salience parameter. We assume
79

that s
DO
is represented by the ratio of the LO size to the DO size because the DO’s
effect was affected by the LO size in our experiment. θ
DO
s
DO
reflects the tendency
shown in Fig. 2 (d).
f
o
= e
α
(x
LO
−x
DO
)
2
}
(7)
f
p
= 1 − x
DO
(8)
f
a
=
γ
1 + e
β(x
LO
−x
DO
)
(9)
Here, f
o
is an effect of an interaction between the LO and DO. The closer the DO is
to the LO, the effect increases. The further the DO is from the LO, the effect decreases
gradually. f
p
is an effect determined by the DO’s distance from the RO. That is, it
includes the effect of the DO absolute position as shown in Fig. 2 (b), where θ
DO
defines
the slope of the curve of each spatial term. On the other hand, f
a
is an asymmetric effect
of the DO, depending on the LO’s position in the RO sides of the DO and the opposite
side. Especially, for t
ˆ
oi (far from), with θ
DO
and C
DO
, f
a
could provide negative effect
when the LO is between the RO and DO, but positive effect when the LO is between
the DO and the farthest point. Using these fundamental attention elements, equation (6)
represents an effect of the DO relative position as shown in Fig. 2 (c).
Table 2. Model parameter estimation and model evaluation.
hidari tikai tˆoi
Parameters (left) (near) (far from)
r
LO
: p -0.232 -1.24 1.226
θ
LO
0.027 0.131 -0.193
C
LO
0.966 0.966 0.039
r
DO
: α 0.02 0.015 0.003
β 70.0 70.0 70.0
γ -2.0 -0.05 -0.05
θ
DO
-0.015 -0.3 0.23
C
DO
-0.02 -0.02 0.05
R
2
r
LO
0.993 0.987 0.986
r
DO
0.772 0.420 0.931
3.2 Simulation and Discussion
We performed a nonlinear regression analysis on our experimental data to estimate the
parameters of r
LO
and r
DO
. Table 2 summarises the resultant parameters. r
LO
’s param-
eters are estimated from the subjects’ mean ratings without the DO. r
DO
’s parameters
are estimated from the difference between the ratings with and without the DO of each
subject. For β and C
DO
, the values shown in Table 2 were given as constraints.
The correlation factor of r
LO
exceeds 0.98 for all spatial terms to verify good preci-
sion. Conversely, r
DO
fits very well for t
ˆ
oi (far from), but does not for hidari (left) and
tikai (near). For hidari (left), the model does not fit the data (r
DO
is largely negative)
when the LO size is large and both the LO and DO are close to the RO. The correlation
factor of the case with LO’s size 1 and 2 increases to 0.510, which suggests room for
further improvement of the model.
80

θ
DO
is negativefor tikai (near) and hidari (left), which works to degrade the goodness-
of-fit of the LO. On the other hand, θ
DO
of t
ˆ
oi (far from) is positive, which increases
the goodness-of-fit of the LO. The absolute values of both θ
LO
and θ
DO
for hidari
(left) are relatively smaller than the others. As the experiment revealed, the effect of
the size of the LO is almost constant for hidari (left), suggesting it would be a specific
characteristic of the projective terms.
4 Related Work
In the previousstudies of computational models of spatial cognition, the AVS (Attention
Vector Sum) model [5] introduced an attention vector on the Spatial Template for the
configuration of two objects. This paper proposed to estimate LO’s goodness-of-fit by
superimposing several different attention factors. The proposed computational model is
the sum of the LO’s goodness-of-fit and the DO’s effect, making it similar to the RPM
for English term near.
In the past study, the salience of objects is considered to come from their attributes
such as the size and colour. In the modeling of attention to the DO, however, those
object attributes are part of geometric factors affecting the spatial term’s goodness-of-
fit. If we generalise the source of salience to consider the salience of objects affected by
the degree of attention to the objects, the salience factor varies depending on the DO’s
position as well for instance. In addition, assuming that attention to an object might
be affected by its linguistic referring expression, the salience factor must be redefined
based on overall properties of objects involving multiple factors: the object size and
position, linguistic expressions, etc.
Carlson-Redvansky and Logan proposed a framework of basic steps for the spatial
cognition process [14]. They focused on the process of recognizing the simple two-
object relation. In the case involving a distractor object, we need to take into account
other factors of visual scenes, such as the specific attention model of each spatial term.
Subsequently, the other factors need to be considered in order to calculate the effect of
the DO against the LO. This paper contributes to reveal these other aspects of the spatial
cognition process.
5 Conclusions and Future Work
This paper proposed a computational model of the goodness-of-fit of spatial terms.
The model incorporates attention to a distractor object, particularly, the effects of their
geometric factors. The proposed model was evaluated by using the experimental data
to confirm its effectiveness.
The following is the agenda for furture work.
– We need to extend the model to deal with the wider scope of geometric factors. For
instance, a situation involving multiple distractors and a situation where objects are
not aligned on a single line should be handled by the model.
– We need to confirm if the model is robust against the change of the distractor size
and the reference object size.
81

– Modeling the change of viewpoint is another issue to be tackled. We analysed this
problem in our previous work [8] using the other two Japanese projective terms:
mae (in front of) and ushiro (back), but we have not incorporated the findings into
the model yet.
– Another challenge is using attention modeling to account for conventional usages
of spatial terms. Herskovits [15] analysed some conventional expressions of spatial
terms in association with the object functions and contexts. Some of these cases
could be explained within the scope of geometric factors. For instance, we say
“the cat is under the table.” instead of “the cat is in the table.”. The preference of
under over in could be explained by an attention model which captures the relations
among objects based on geometric factors (the shape of the table in this case) to
which human attention is directed. In this instance, the table top is more salient to
attract human attention, thus relation under could be preferred for describing the
relation between the cat and the table (top).
References
1. Hayward, W.G., Tarr, M.J.: Spatial language and spatial representation. Cognition 55 (1995)
39–84
2. Logan, G.D., Sadler, D.D.: A computational analysis of the apprehension of spatial relations.
In Bloom, P., Peterson, M.A., Nadel, L., Garrett, M., eds.: Language and Space. The MIT
Press (1996) 493–529
3. Gapp, K.P.: Basic meanings of spatial relations: Computation and evaluation in 3d space. In:
Proceedings of AAAI-94. (1994) 1411–1417
4. Kelleher, J., Kruijff, G.J., Costello, F.J.: Proximity in context: An empirically grounded com-
putational model of proximity for processing topological spatial expressions. In: Proceedings
of the 21st International Conference on Computational Linguistics and 44th Annual Meeting
of the Association for Computational Linguistics. (2006) 745–752
5. Regier, T., Carlson, L.A.: Grounding spatial language in perception: An empirical and com-
putational investigation. Journal of Experimental Psychology: General 130 (2001) 273–298
6. Tokunaga, T., Koyama, T., Saito, S., Nakajima, M.: Classification of japanese spatial nouns.
In: Proceedings of 4th International Conference on Language Resources and Evaluation
(LREC 2004). (2004) 1829–1832
7. Coventry, K.R., Garrod, S.C.: Saying, Seeing, and Acting: The Psychological Semantics of
Spatial Prepositions. Psychology Press (2004)
8. Kobayashi, T., Terai, A., T., T.: The effect of geometric factors on spatial term selection.
Cognitive Studies 15 (2008) 144–160 (in Japanese).
9. Kobayashi, T., Terai, A., T., T.: On the effect of geometric factors on spatial term selection.
In: Proceedings of 14th Annual Meeting of Association of Natural Language Processing
(Japan). (2008) 689–692 (in Japanese).
10. Carlson, L.A., Logan, G.D.: Using spatial terms to select an object. Memory & Cognition
29 (2001) 883–892
11. Kelleher, J., van Genabith, J.: A computational model of the referential semantics of pro-
jective prepositions. In Saint-Dizier, P., ed.: Computational Linguistics: Dimensions of the
Syntax and Semantics of Prepositions. Kluwer Academic Press (2005) 211–228
12. Kojima, T., Kusumi, T.: The effect of the extra object on the linguistic apprehension of spatial
relationship between two objects. Spatial Cognition and Computation (2006) 145–160
82

13. Kelleher, J., Kruijff, G.J.: Incremental generation of spatial referring expressions in situated
dialogue. In: Proceedings of the 21st International Conference on Computational Linguistics
and 44th Annual Meeting of the Association for Computational Linguistics. (2006) 1041–
1048
14. Carlson-Radvansky, L.A., Logan, G.D.: The influence of reference frame selection on spatial
template construction. Journal of Memory and Language 37 (1997) 411–437
15. Herskovits, A.: On the spatial uses of prepositions. In: Proceedings of 18th Annual Meeting
of ACL. (1980) 1–5
83
