COMPARISION OF K-MEANS AND PAM ALGORITHMS

USING CANCER DATASETS

Parvesh Kumar and Siri Krishan Wasan

Department of Mathematics, Jamia Milia Islamia, New Delhi, India

Keywords: Data mining, Clustering, k-means, PAM.

Abstract: Data mining is a search for relationship and patterns that exist in large database. Clustering is an important

datamining technique . Because of the complexity and the high dimensionality of gene expression data,

classification of a disease samples remains a challenge. Hierarchical clustering and partitioning clustering is

used to identify patterns of gene expression useful for classification of samples. In this paper, we make a

comparative study of two partitioning methods namely k-means and PAM to classify the cancer dataset.

1 INTRODUCTION

According to Usama Fayyad et al. (Fayyad,1996),

“Data mining is a step in the KDD (Knowledge

Discovery in Databases) process that consists of

applying data analysis and discovery algorithms that

produce a particular enumeration of patterns (or

models) over the data”.

According to Guha et al. (Guha,1998), “

Clustering problem is about partitioning a given data

set into groups (clusters) such that the data points in

a cluster are more similar to each other than points

in different clusters “ . A mathematical definition of

clustering is the following : let X = { x

, x

…… , x

m-1

, x

} ⊂ R

set of data items

representing a set of m points x

in R

where x

= {

, x

, …… , x

} . The goal is to partition X

into k-groups { C

: 1 ≤ i ≤ k } such that data

belong to the same group are more “alike" than data

in different groups. Each of the k-groups is called a

cluster. The result of the algorithm is an injective

mapping of data items x

to groups C

Partitional clustering algorithms divide the whole

data set into a set of disjoint clusters directly. These

algorithms attempt to determine an integer number

of clusters that optimise a certain objective function

through an iterative procedure.

To classify the various types of cancer into its

different subcategories, different data mining

techniques have been used over gene expression

data. Gene expression data, obtained using gene

expression monitoring by DNA microarrays,

provides an important source of information that can

help in understanding many biological processes. A

common aim, then, is to use the gene expression

profiles to identify groups of genes or samples in

which the members behave in similar ways. One

might want to partition the data set to find naturally

occurring groups of genes with similar expression

patterns. Golub et al (Golub,1999), Alizadeh et al

(Alizadeh,2000), Bittner et al (Bittner,2000) and

Nielsen et al (Nielsen,2002) have considered the

classification of cancer types using gene expression

datasets. There are many instances of reportedly

successful applications of both hierarchical

clustering and partitioning clustering in gene

expression analyses. Yeung et al (Yeung,2001)

compared k-means clustering, CAST (Cluster

Affinity Search Technique), single-, average- and

complete-link hierarchical clustering, and totally

random clustering for both simulated and real gene

expression data. And they favoured k-means and

CAST. Gibbons and Roth (Gibbons,2001) compared

k-means, SOM ( Self-Organizing Map ) , and

hierarchical clustering of real temporal and replicate

microarray gene expression data, and favoured k-

means and SOM.

In this paper, we make a comparative study of

two clustering algorithms namely k-means and PAM

to classify the cancer datasets and is based on

accuracy and ability to handle high dimensional

data.

255

Kumar P. and Krishan Wasan S. (2008).

COMPARISION OF K-MEANS AND PAM ALGORITHMS USING CANCER DATASETS.

In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 255-258

DOI: 10.5220/0001868602550258

 SciTePress

2 K-MEANS ALGORITHM

The k-means algorithm is a partitioning clustering

algorithm. The k -means algorithm is very simple

and most popular clustering algorithm. The k-means

algorithm is a squared error-based clustering

algorithm.

The k-means is given by MacQueen

(MacQueen,1967) and aim of this clustering

algorithm is to divide the dataset into disjoint

clusters by optimizing an objective function that is

given below

Optimize

∑∑

=∈

icix

mixdE

),(

(1)

Here m

is the center of cluster C

, while d(x,m

)

is the euclidean distance between a point x and

cluster center m

. In k-means algorithm, the

objective function E attempts to minimize the

distance of each point from the cluster center to

which the point belongs.

Consider the data set with ‘n’ objects ,i.e.,

S = {x

: 1 ≤ i ≤ n}.

1) Initialize k-partitions randomly or based on some

prior knowledge.

i.e. { C

, C

, …….., C

2) Calculate the cluster prototype matrix M (distance

matrix of distances between k-clusters and data

objects) .

M = { m

, m

, …….. , m

} where m

is a

column matrix 1 × n .

3)Assign each object in the data set to the nearest

cluster - Cm i.e. x

∈C

if d(x

) ≤ d(x

) ∀

1 ≤ j ≤ k , j ≠m where j=1,2,3,…….n.

4) Calculate the average of cluster elements of each

cluster and change the k-cluster centers by their

averages.

5) Again calculate the cluster prototype matrix M.

6) Repeat steps 3, 4 and 5 until there is no change

for each cluster.

3 PAM ALGORITHM

The purpose for the partitioning of a data set into k

separate clusters is to find groups whose members

show a high degree of similarity among themselves

but dissimilarity with the members of other groups.

The objective of PAM(Partitioning Around

Medoids) (Kaufman,1990) is to determine a

representative object (medoid) for each cluster, that

is, to find the most centrally located objects within

the clusters. Initially a set of k-items is taken to be

the set of medoids. Then, at each step, all objects

from the input dataset that are not currently medoids

are examined one by one if they should be

medoids.That is the algorithm determines whether

there is an object that should replace one of the

existing medoids . Swapping of medoids with other

non-selected objects is based on the value of total

cost of impact T

.The PAM represents a cluster by

a medoid so PAM is also known as k-medoids

algorithm.

The PAM algorithm consists of two parts. The first

build phase follows the following algorithm:

Phase-1:

Consider an object i as a candidate.Consider another

object j that has not been selected as a prior

candidate. Obtain its dissimilarity d

with the most

similar previously selected candidates. Obtain its

dissimilarity with the new candidate i. Call this d(j;

i): Take the difference of these two dissimilarities.

1) If the difference is positive, then object j

contributes to the possible selection of i.

Calculate C

= max (d

- d(j; i); 0) where d

– Euclidian distance between j

object and

most similar previously selected candidate

and d(j; i) – Euclidian distance between j

and i

object .

2) Sum Cji over all possible j.

3) Choose the object i that maximizes the sum

of C

over all possible j.

4) Repeat the process until k objects have been

found.

Phase-2:

The second step attempts to improve the set of

representative objects. This does so by considering

all pairs of objects (i; h) in which i has been chosen

but h has not been chosen as a representative. Next it

is determined if the clustering results improve if

object i and h are exchanged. To determine the

effect of a possible swap between i and h we use the

following algorithm:

Consider an object j that has not been previously

selected. We calculate its swap contribution C

jih

1) If j is further from i and h than from one of the

other representatives, set C

jih

to zero.

2) If j is not further from i than any other

representatives (d(j;i)=d

), consider one of two

situations:

a) j is closer to h than the second closest

representative & d(j; h) < E

where E

is the

Euclidian distance of between j

object and the

second most similarly representative . Then

jih

= d(j; h)-d(j; i).

Note: C

jih

can be either negative or positive

depending on the positions of j, i and h. Here only if

ICSOFT 2008 - International Conference on Software and Data Technologies

256

j is closer to i than to h is there a positive influence

at implies that a swap between object i and h are a

disadvantage in regards to j.

b) j is at least as distant from h than the second

closest representative( d(j; h) >=Ej ).Let Cjih =

Ej - dj. The measure is always positive,

because it not wise to swap i with h further

away from j thane second closest

representative.

3) If j is further away from i than from at least one of

the other representatives, but closer to h than to any

other representative, C

jih

= d(i; h) - d

will be the

contribution of j to the swap.

4) Sum the contributions over all j. T

= ∑ C

jih

. This

indicates the total result of the swap.

5) Select the ordered pair (i; h) which minimizes T

ih.

6) If the minimum T

is negative, the swap is carried

out and the algorithm returns to the first step in the

swap algorithm. If the minimum is positive or 0, the

objective value cannot be reduced by swapping and

the algorithm ends.

4 CANCER DATASETS USED

FOR COMPARISION OF

K-MEANS AND PAM

We used three different datasets to make a

comparision study between k-means and PAM

algorithms .Brief description is given below :

The Leukemia data set is a collection of gene

expression measurements from 72 leukemia

(composed of 62 bone marrow and 10 peripheral

blood) samples reported by Golub.

It contains an initial initial training set composed

of 47 samples of acute lymphoblastic leukemia

(ALL) and 25 samples of acute myeloblastic

leukemia (AML).

Figure 1: Graphical representation of Leukemia dataset.

The Colon dataset is a collection of gene

expression measurements from 62 Colon biopsy

samples from colon-cancer patients reported by

Alon. Among them, 40 tumor biopsies are from

tumors (labelled as "negative") and 22 normal

(labelled as "positive") biopsies are from healthy

parts of the colons of the same patients. Two

thousand out of around 6500 genes were selected

The Lymphoma dataset is a collection of gene

expression measurements from 96 normal and

diffused malignant lymphocyte samples reported by

Alizadeh. It contains 42 samples of diffused large B-

cell lymphoma (DLBCL) and 54 samples of other

types. The Lymphoma data set contains 4026 genes.

5 RESULTS

5.1 Comparison of k-means and PAM

for Gene-leukemia Dataset

Here we apply k-means and PAM algorithms on

leukemia data set to classify it into two equivalent

classes . We use two variations of leukemia data set

one with 50-genes and another with 3859-genes.

Table 1: Results for 50-gene-leukemia dataset.

Results of k-means & PAM using 50-gene-leukemia

Total Number of records in dataset = 72

Clustering

Algorithm

Correctly

Classified

Average Accuracy

k-means 69 95.83

PAM 64 88.89

We observe that k-means algorithm converges

fast in comparision to PAM algorithm . In this case,

accuracy for k-means is also better than the accuracy

of PAM algorithm.

Graphical representation of two cluster centers of

50-gene-leukemia data set using k-means and PAM

algorithm is shown below:

cluster center using k-means

0.00E+ 00

1.00E-01

2.00E-01

3.00E-01

4.00E-01

5.00E-01

6.00E-01

7.00E-01

8.00E-01

1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70

Gene Number

Gene Express ion Val ue

Figure 2: Graph of cluster centers using k-means.

Cluster centers using PAM

2000

4000

6000

8000

10000

12000

1 4 7 101316192225283134374043464952555861646770

Gene Number

Gene Expressi on Val ue

Figure 3: Graph of cluster centers using PAM.

COMPARISION OF K-MEANS AND PAM ALGORITHMS USING CANCER DATASETS

257

When we apply these algorithms on 3859-gene-

leukemia dataset results are different as compared to

results with 50-gene-leukemia dataset. In this case

PAM algorithm’s accuracy is better than k-means

algorithm’s accuracy. This shows that PAM perform

better when we increase number of attributes.

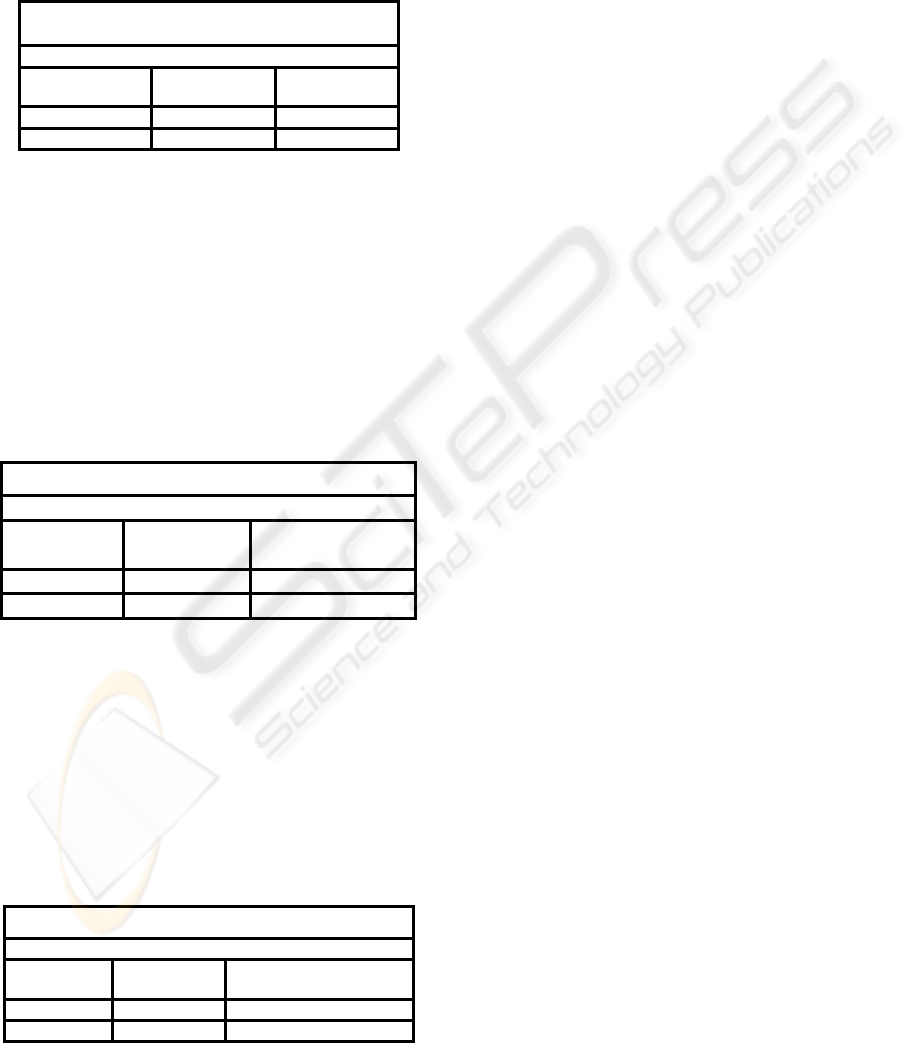
Table 2: Results for 3859-gene-leukemia dataset.

Results of k-means and PAM using

3859-gene-leukemia

Total number of records in dataset = 72

Clustering

Algorithm

Correctly

Classified

Average

Accuracy

k-means 61 84.72

PAM 68 94.44

5.2 Comparison of K-means and PAM

for 2000-Gene-colon Dataset

Analysis of 2000-gene-colon data set is also done

with the help of these two partitioning algorithms

i.e. k-means and PAM algorithm. In this case PAM

algorithm performs better then k-means method. But

accuracy difference between these algorithms over

colon data set is significantly low. Average accuracy

remains low.

Table 3: Results for 2000-gene-colon dataset.

Results of k-means and PAM using 2000-gene-colon

Total number of records in dataset = 62

Clustering

Algorithm

Correctly

Classified

Average Accuracy

k-means 33 53.22

PAM 34 54.84

5.3 Comparison of K-means and PAM

for 4026-Gene-lymphoma Dataset

Using these algorithms , we divide the whole dataset

into two different clusters which are used to

differentiate between normal and diffused samples .

Here PAM algorithm correctly classifies 77 records

out of 96 whereas k-means algorithm correctly

classifies 71 records

Table 4: Results for 4026-gene-dlbcl dataset.

Results of k-means and PAM using 4026-gene-dlbcl

Total number of records in dataset = 96

Clustering

Algorithm

Correctly

Classified

Average Accuracy

k-means 71 73.96

PAM 77 80.21

So it is clear that PAM performs better when we

increase the number of genes.

6 SUMMARY

Algorithm’s comparision shows that accuracy of

PAM is better from accuracy of k-means as number

of objects in the dataset increases. In case of k-

means intial selection of cluster centres plays a very

important role. So there is a possibility to improve

both algorithms by using some good initial selection

technique. Here in this paper PAM performs better

in the classification of cancer types using cancer

datasets than k-means.

REFERENCES

Alizadeh A.A, Eisen M.B, Davis R.E, et al. Distinct types

of diffuse large B-cell lymphoma identified by gene

expression profiling. Nature. 2000;403(6769):503–

511.

Bittner M, Meltzer P, Chen Y, et al. Molecular

classification of cutaneous malignant melanoma by

gene expression profiling. Nature.

2000;406(6795):536–540.

Fayyad, M.U., Piatesky-Shapiro, G., Smuth P.,

Uthurusamy, R. (1996). Advances in Knowledge

Discovery andData Mining. AAAI Press.

Gibbons F.D, Roth F.P. Judging the quality of gene

expression-based clustering methods using gene

annotation. Genome Res. 2002;12(10):1574–1581.

Golub T.R, Slonim D.K, Tamayo P, et al. Molecular

classification of cancer: class discovery and class

prediction by gene expression monitoring. Science.

1999;286(5439):531–537.

Guha, S., Rastogi, R., and Shim K. (1998). CURE: An

Efficient Clustering Algorithm for Large Databases. In

Proceedings of the ACM SIGMOD Conference.

L. Kaufman and P. J. Rousseeuw, Finding Groups in Data:

an Introduction to Cluster Analysis, John Wiley &

Sons, 1990.

MacQueen, J.B. (1967). Some Methods for Classification

and Analysis of Multivariate Observations. In

Proceedings of 5th Berkley Symposium on

Mathematical Statistics and Probability, Volume I:

Statistics, pp. 281–297.

Nielsen T.O, West R.B, Linn S.C, et al. Molecular

characterisation of soft tissue tumours: a gene

expression study. Lancet. 2002;359(9314):1301–1307.

Yeung K.Y, Haynor D.R, Ruzzo W.L. Validating

clustering for gene expression data. Bioinformatics.

2001;17(4):309–318.

ICSOFT 2008 - International Conference on Software and Data Technologies

258