
FUZZY
TIME MANIPULATION IN A RELATIONAL DB
N. Mar
´
ın
1
, J. M. Medina
1
, O. Pons
1
and M. C. Garrido
2
1
Dept. of Computer Science and Artificial Intelligence, University of Granada, ETSI Inform
´
atica, Spain
2
Junta de Andaluca, Spain
Keywords:
Fuzzy Data, Temporal Database, Fuzzy Interval, Data Manipulation.
Abstract:
Temporal Databases (TDB) have as a primary aim to offer a common framework to those DB applications that
need to store or handle temporal data of different nature or source, since they allow to unify the concept of
time from the point of view of its meaning, its representation and its manipulation. Up to now, most of the
efforts have been devoted to extend the relational model in order to be adapted to the new way of inserting,
deleting and updating the DB, together with the integrity constraints involved. In this paper we deal with these
problems when the time is imprecisely expressed by means of a fuzzy interval of dates. Along the text, we
will see how the delete and the insert operations can be carried out and how different types of queries to such
a fuzzy temporal database are solved.
1 INTRODUCTION
Temporal Databases, in the widest sense, offer a com-
mon framework for all database applications that in-
volve some temporal aspects when organizing data.
These databases allow to unify the time concept from
several points of view: the representation, the seman-
tics and the manipulation.
Database applications involving temporal data are
not a new subject and up to now, most of the work
-both theoretical and implementations- made on this
topic has been carried out using as starting point the
relational DB model (since it is the most complete and
consolidated one) and base the results in the extension
of the table schemata (Tansel et al., 1993), the range
of operators to be used (Elmarsi and Wuu, 1990) and
in the addition of specific integrity constraints related
to the new data types (Snodgrass et al., 1995), (Etzion
et al., 1998),(Bettini et al., 1998).
From the point of view of the real world, there ex-
ist two basic ways for associating temporal concepts
to a fact:
1. Punctual Facts. a fact is related to an only time
mark that depends on the granularity and informs
about the time when it happened. As instances,
birthdays, the order date, an academic year, ...
2. Time Periods. that are represented by a starting in-
stant and an ending one, so the duration (or valid
time) of the fact is implicit. Some examples are:
[admission date, discharge date], [start contract
date, end contract date], ...
This way of time interpretation is called valid
time.
For example, in the valid time relation (VTR)
EMP each tuple represents a version for the avail-
able information about an employee, and this version
is valid only when used in the time interval [VST,
VET]. The up-to-date version, also called valid tuple,
is indefinite-valued in the attribute VET. In the figure
1 an instance of EMP is shown.
Table 1: Instance example of the valid time relation EMP.
N
AME
ID SAL. BOSS EXP
.
VST VET
GRANT 1245 1500 9877 TRAINEE 15-06-97 31-05-98
GRANT 1245 1800 9877 JUNIOR 01-06-98 Undefined
REDFORD 9877 1200 4588 TRAINEE 20-08-94 31-01-96
REDFORD 9877 1500 4588 JUNIOR 01-02-96 31-03-97
REDFORD 9877 2200 9989 SENIOR 01-04-97 Undefined
BR
OWN
1278 2800 4588 JUNIOR 01-05-05 10-08-08
STREEP 6579 4000 9877 TRAINEE 15-06-97 Undefined
At
first sight, time inclusion into a DB seems to
be easy and direct, but extending schemata with these
new attributes have many complex consequences,
such as:
• In a VTR, the old primary key is not unique. The
new primary key is the result of combining the
previous value for the key and one of the valid
time attributes, VST or VET. If the case of the
employees table EMP is considered, the primary
91
Marín N., M. Medina J., Pons O. and C. Garrido M. (2008).
FUZZY TIME MANIPULATION IN A RELATIONAL DB.
In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 91-97
DOI: 10.5220/0001870200910097
Copyright
c
SciTePress
key is not EMPID (employee’s code) but EM-
PID+VST or EMPID+VET.
• There can only exist a valid tuple for each entity
in a concrete moment. Because of this, every op-
eration has to be strictly controlled because valid
time periods of distinct versions of the same entity
must not overlap.
• Internal implementation of common operations is
completely different to those implemented within
a non temporal database. For instance, when an
UPDATE is required, a new version of the updated
tuple is created and the up-to-now valid version of
the tuple is closed by fixing its VET value with
the final time. In this case, the user is responsible
for giving the valid time for an update operation;
when closing the active version, the value of the
attribute VET is updated with the previous grain
to the value for VST attribute in the new version.
Together with these special consideracions, some-
times it is not possible for the user to give an exact
but an imprecise starting/ending point for the valid-
ity period of a fact. This is the case, for example,
when a patient does not exactly know when a con-
crete ailment or symptom started. In this case, the
use of fuzzy sets theory is necessary for not missing
such important information since fuzzy time values
can be used. Many authors working in the area of soft
computing have opted to study temporal data affected
by imprecision and/or uncertainty. That is the case of
the paper (Chountas and Petrounias, 2005) what deals
with this problem from the point of view of uncer-
tainty exclusively, by attaching a probability distribu-
tion to every temporal data. Also in (Tre et al., 1997)
the problem of fuzzy time is addressed in an object-
oriented DB system and some interesting results have
been obtained.
This paper is devoted to the fuzzy representation
of time together with the UPDATE and the SELECT
operation when the time is expressed in fuzzy terms.
Note that the study of the UPDATE operation includes
also the DELETE and the INSERT operations as par-
ticular cases so that the results obtained can be extrap-
olated to the whole data manipulation language.
1.1 Previous Concepts on Fuzzy Sets
A fuzzy value is a fuzzy representation about the real
value of a property (attribute) when it is not precisely
known.
In this paper, according to Goguen’s Fuzzification
Principle (Goguen, 1967), we will call every fuzzy
set of the real line fuzzy quantity. A fuzzy number is a
particular case of a fuzzy quantity with the following
properties:
Definition 1. The fuzzy quantity A with membership
function µ
A
(x) is a fuzzy number (Dubois and Prade,
1985) iff:
1. ∀ α ∈ [0,1], A
α
= {x ∈ R | µ
A
(x) ≥ α} (α-cuts of
A) is a convex set.
2. µ
A
(x) is an upper-semicontinuous function.
3. The support set of A, defined as Supp(A) = {x ∈
R | µ
A
(x) > 0}, is a bounded set of R, where R is
the set of real numbers.
We will use
∼
R
to denote the set of fuzzy numbers,
and h(A) to denote the height of the fuzzy number A.
For the sake of simplicity, we will use capital letters at
the beginning of the alphabet to represent fuzzy num-
bers.
A
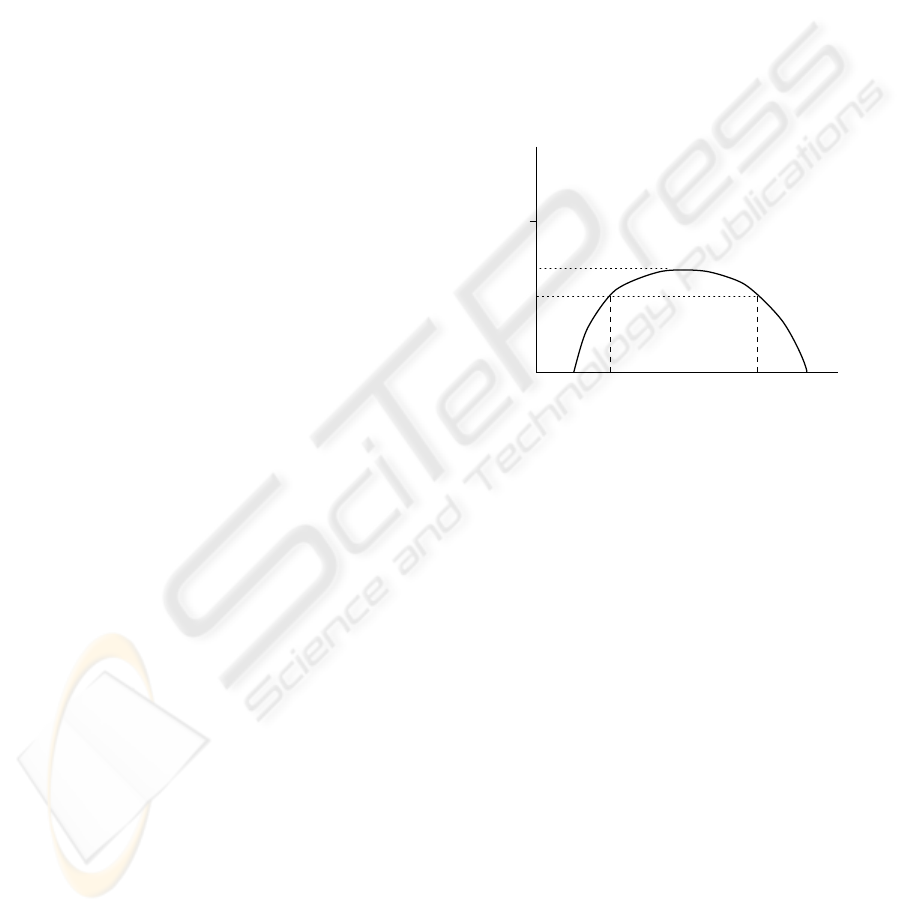
h(A)
α
1
α
ba
α
Figure 1: Fuzzy number.
The interval [a
α
,b
α
] (see figure 1) is called the α-
cut of A. So then, fuzzy numbers are fuzzy quantities
whose α-cuts are closed and bounded intervals: A
α
=
[a
α
,b
α
] with α ∈ (0, 1].
If there is, at least, one point x verifying µ
A
(x) = 1
we say that A is a normalized fuzzy number.
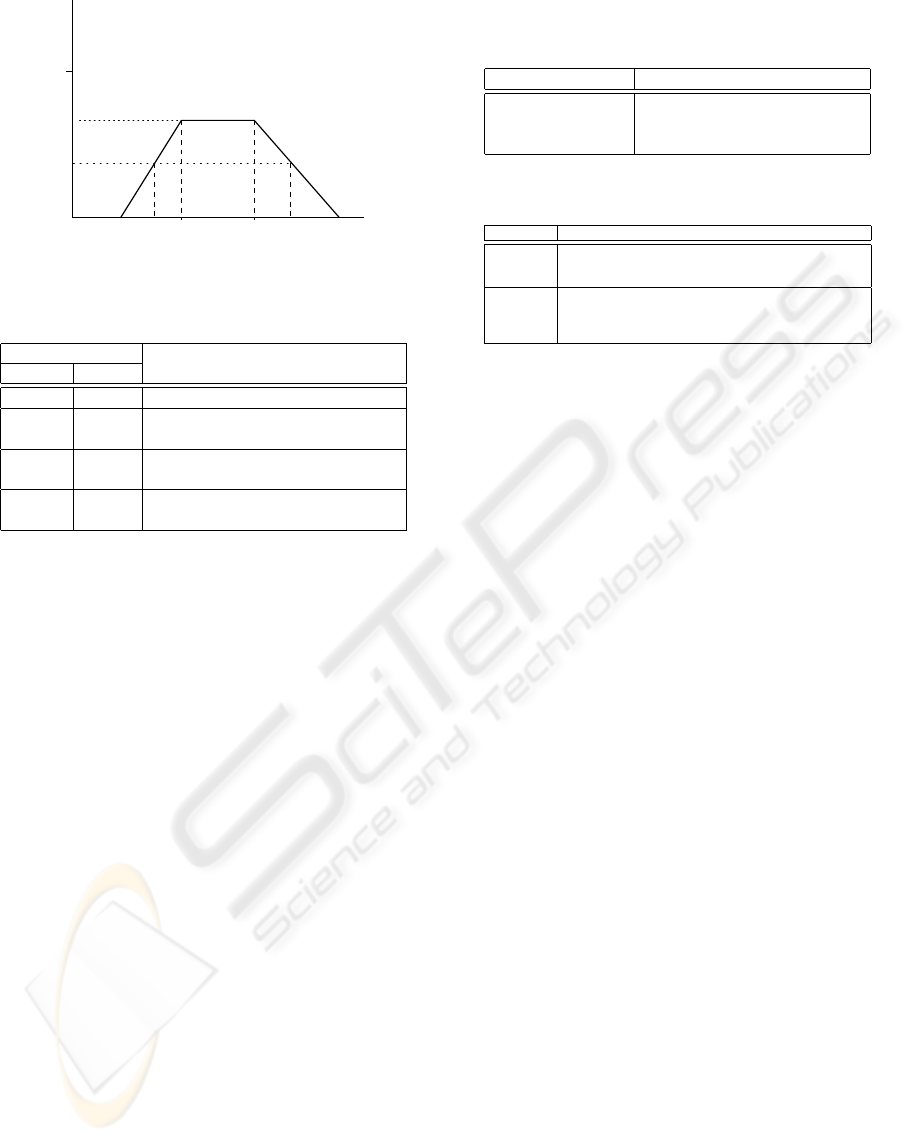
Sometimes, a trapezoidal shape is used to repre-
sent fuzzy values. This representation is very useful
as the fuzzy number is completely characterized by
four parameters (m
1
,m
2
,a,b) as shows figure 2 and
the height h(A) when the fuzzy value is not normal-
ized. We will call modal set all values in the interval
[m
1
,m
2
], i.e, the set {x ∈ Supp(A) | ∀ y ∈ R, µ
A
(x) ≥
µ
A
(y)}. The values a and b are called left and right
spreads, respectively.
In our approach, we will use trapezoidal and nor-
malized fuzzy values.
1.2 FSQL (Fuzzy SQL)
The FSQL language (Galindo et al., 1998),(Galindo
et al., 2006) extends the SQL language in order to ex-
press flexible queries. Due to its complex format, we
only show here an abstract with the main extensions
to the
select
command.
ICSOFT 2008 - International Conference on Software and Data Technologies
92
1
A
m -a m
α
a
α α
m
2
m +b
1 1 2
b
h(A)
Figure 2: Trapezoidal fuzzy number.
Table 2: Fuzzy Comparators for FSQL (Fuzzy SQL).
Comparator for:
Possibility Necessity Significance
FEQ NFEQ
Fuzzy EQual (Possibly/Necessarily Equal)
FGT NFGT
Fuzzy Greater Than
FGEQ NFGEQ
Fuzzy Greater or Equal
FLT NFLT
Fuzzy Less Than
FLEQ NFLEQ
Fuzzy Less or Equal
MGT NMGT
Much Greater Than
MLT NMLT
Much Less Than
• Linguistic Labels. These labels will be preceded
by the symbol
$
to distinguish them easily and
have associated a trapezoidal possibility distribu-
tion. So, for example, we can define the labels
$Short
,
$Normal
,
$Tall
, ... on the
Height
at-
tribute.
• Fuzzy Comparators. Besides the typical com-
parators (
=
,
>
...), FSQL includes the fuzzy com-
parators shown in table 2. Like in SQL, fuzzy
comparators compare one column with one con-
stant or two columns of the same type.
Possibility comparators are less restrictive than
necessity comparators are. For example,
NFEQ
uses the following equation:
Θ
NFEQ
(
e
p,
e
p
0
) = inf
d∈U
max (1− µ
e
p
(d), µ
e
p
0
(d)) (1)
• Fulfilment Thresholds. (γ) For each simple con-
dition a fulfilment threshold may be established
(default is 1) with the format:
<condition> THOLD
γ
indicating that the condition must be satisfied with
minimum degree γ ∈ [0,1] to be considered. The
reserved word
THOLD
is optional and may be sub-
stituted by a traditional crisp comparator (=, ≤...).
Find the people that are necessarily taller than la-
bel
$Tall
(in minimum degree 0.8):
Table 3: Default computation for function
CDEG
with logic
operators in FSQL.
<Condition> CDEG(<Condition>)
<cond1> AND <cond2>
min(
CDEG(<cond1>)
,
CDEG(<cond2>)
)
<cond1> OR <cond2>
max(
CDEG(<cond1>)
,
CDEG(<cond2>)
)
NOT <cond1>
1 -
CDEG(<cond1>)
Table 4: Fuzzy constants that may be used in FSQL queries.
F. Constant Significance
UNKNOWN
Unknown value but the attribute is applicable.
UNDEFINED
The attribute is not applicable or it is meaningless.
NULL
Total ignorance: We know nothing about it.
$[a,b,c,d]
Fuzzy trapezoid (
a
≤
b
≤
c
≤
d
).
$label
Linguistic Label: It may be a trapezoid or a scalar.
[n,m]
Interval “Between
n
and
m
” (
a
=
b
=
n
and
c
=
d
=
m
).
#n
Fuzzy value “Approximately
n
” (
b
=
c
=
n
and
n
–
a
=
d
–
n
=margin).
SELECT * FROM Person WHERE Height NFGT $Tall
THOLD 0.8
• Function CDEG(<attribute>). It shows a
column with the fulfilment degree of the condi-
tion imposed on a specific attribute. If logic oper-
ators appear, the calculation of this compatibility
degree is carried out as table 3 shows. We use the
minimum T-norm and the maximum T-conorm,
but the user may change these values by modi-
fying a view (
FSQL_NOTANDOR
). In this view the
user can set the function to be used for every logic
operator (NOT, AND, OR). Obviously, that func-
tion must be implemented in the FSQL Server or
by the user himself.
• Fuzzy Constants. In FSQL we can use the fuzzy
constants detailed in table 4.
2 FUZZY TIME
REPRESENTATION
In the introduction we have seen that, in classical
TDB, the valid time is managed thanks to the exten-
sion of the tables schemata by adding two new at-
tributtes, the valid start time -VST- and the valid end
time -VET- to determine the period of validity of the
fact expressed by a tuple.
In this paper we are going to consider that the in-
formation provided by the VST and VET for the clas-
sical TDB is fuzzy, in the sense that we are not com-
pletely sure about when the current values of the tuple
began to be valid.
The more immediate solution to this problem is to
soften the VST and the VET in such a way that they
may contain fuzzy dates represented by means of a
fuzzy number. This means that, if we use the para-
FUZZY TIME REPRESENTATION AND HANDLING IN A RELATIONAL DB
93
metrical representation for fuzzy numbers, we need to
store four values for the VST and four values for the
VET, as shown in figure 3. Since the meaning of the
attributes VST and VET is the period of time during
which the values of a tuple are valid, it is more conve-
nient to summarize the information given by the two
fuzzy attributes in an only but fuzzy interval. This sit-
uation can be represented by the trapezoidal fuzzy set
shown in figure 4 which incorporates the semantics of
our problem. As can be seen in such figure, the right
side of the interval (VET) is set to 1 indefinitely while
the tuple remains valid. On the contrary, the left side
of the interval is the part that reflects the imprecision
about the starting time point of the interval or VST.
In this figure, the fuzzy value represents an interval
where the VST corresponds to middle february and
the VET corresponds to now or indefinitely.
9877
9877
BOSS
JUNIOR
TRAINEE
EXPERTISE
~ 31-05-1998~15-06-199715001245
GRANT
~undefined~01-06-199815001245
GRANT
VETVSTSALARYEMPIDEMPNAM
9877
9877
BOSS
JUNIOR
TRAINEE
EXPERTISE
~ 31-05-1998~15-06-199715001245
GRANT
~undefined~01-06-199815001245
GRANT
VETVSTSALARYEMPIDEMPNAM
(01-06-1998,01-06-1998,2,2)
(31-12-2050,31-12-2050,0,0)
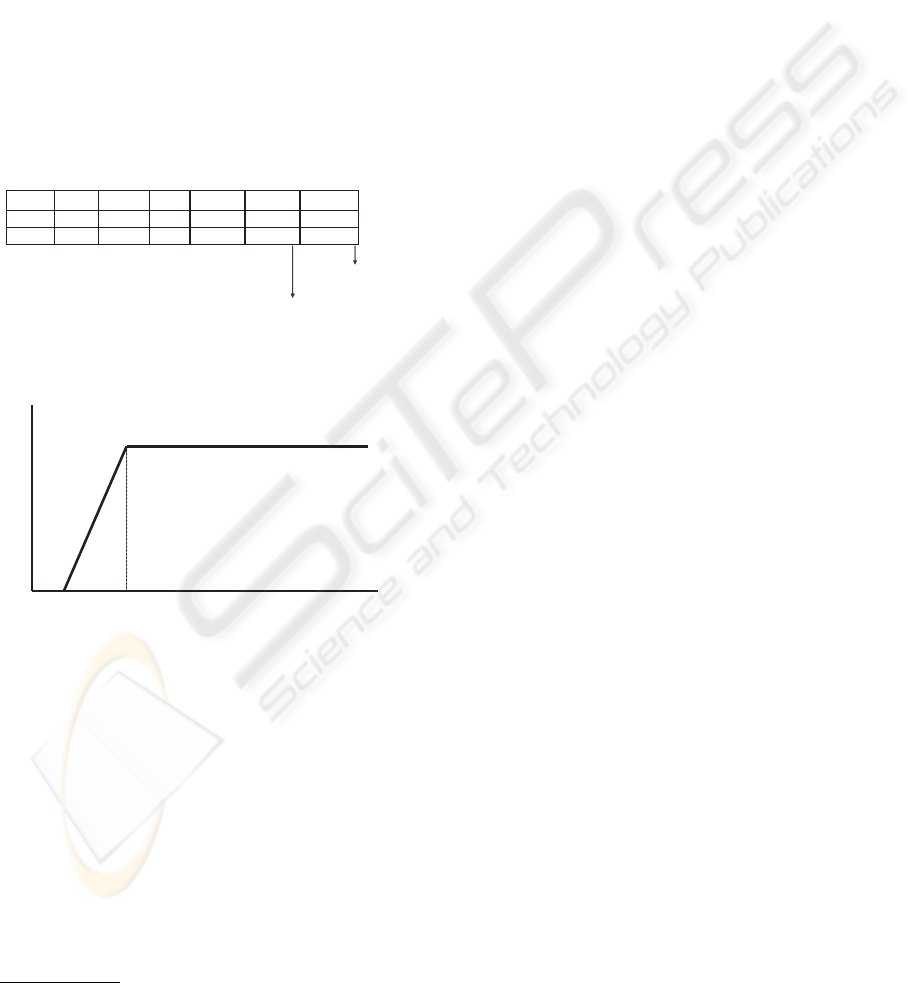
Figure 3: Internal representation of a fuzzy date.
01/06/199830/05/1998
1
Days
31/12/2050
Figure 4: Fuzzy Period of Time for a Valid Tuple.
This representation has the advantage that, not
only periods of time, but fuzzy dates can also be rep-
resented in a unified way. Think that a parametrical
representation as (m,m,a,b) represents a central time
point with some imprecision at both sides, what is in-
terpreted as a fuzzy date.
As it was explained in section 1.2, it is
quite easy to represent a fuzzy interval with this
characteristics since only four parameters need to
be stored in order to specify it. In our ex-
ample, the parametrical representation should be
(17/02/1996,31/12/2050,5,0)
1
. This representation is
more flexible, since admits to represent both precise
1
We have assumed that 31/12/2050 is the ending point
of the time domain
and imprecise time intervals. For example, a precise
interval like [18/03/1997,25/06/1998] is represented
as (18/03/1997,25/06/1998,0,0).
In (Medina et al., 1994), (Medina et al., 1995) is
presented a generalized model of fuzzy DB that sup-
ports this representation for fuzzy data and the corre-
sponding implementation in a classical relational DB
system (Oracle).
3 INSERTING AND UPDATING IN
THE FUZZY TDB
As we explained in the introduction, in a TDB in-
formation is never deleted when an update operation
is being carried out. The process now is to leave
the old version of data in the DB and to add a new
version with the suitable modifications achieved, but
closing the old one by adding a valid end time value
which is the immediately previous granule to the valid
start time of the tuple inserted. Note that closing the
old version of a tuple is a deletion operation in the
TDB environment whereas adding a new version cor-
responds to an insert operation.
One the most important problems that arise when
the time period considered is fuzzy is that we can not
say which is the time point immediately previous to
a given one for a concrete granularity, since many
values with different possibility degree are possible.
To compute this value is very important for the update
operation since, as explained below, we need to close
the old version for the new one is valid. So now, the
given solution is not precise but also imprecise.
Definition 2. Let us note by µ
O
(x) the membership
function associated to the fuzzy interval of the old
version of the tuple to be updated and µ
N
(x) the mem-
bership function associated to the new fuzzy interval.
Then, the membership function of the fuzzy interval
(µ
0
O
(x)) that serves to close the validity time of the old
one is:
µ
0
O
(x) =
½
µ
O
(x) ∀x | µ
N
(x) = 0
1 − µ
N
(x) ∀x | µ
N
(x) > 0
This result can be graphically seen in figure 5.
It is obvious, that the non-overlapping condition
required for the crisp TDB is not valid now, but the
overlapping degree will never reach value 1 for the
sake of consistency.
ICSOFT 2008 - International Conference on Software and Data Technologies
94

17/02/199612/02/1996
1
Days
31/12/2050
10/03/1996
µ
O'
(x) µN(x)
01/03/1996
Figure 5: Membership function of the fuzzy value O’ that
closes a version of a tuple with new valid time N.
Definition 3. We will call closing interval all the val-
ues x ∈ D such that 0 < µ
N
(x) < 1 and 0 < µ
0
O
(x) < 1.
As can be observed, in the closing interval of the
domain D, the more is the possibility to belong to the
new interval, the less is the possibility to belong to the
old one, what makes sense because, for the old valid
time the interval is finishing whereas for the new valid
time it is starting.
It is also important to note that we have used 1 −
µ(x) as the complement of a fuzzy set (it is not the
only possible function in the literature) because it is
the simplest one from the computational point of view
and easy to be understood for a user since it directly
reflects the semantics of the problem.
4 QUERYING THE FUZZY TDB
Once we are able to represent fuzzy periods of valid
time, queries about a crisp/fuzzy date or period to the
valid time relations can be solved computing the cor-
responding fulfillment degree between the time we
are querying about (QT) and the database valid time
(FVP). In the next section we explain the most repre-
sentative types of queries.
In order to illustrate all the cases, let us consider
the following fuzzy TDB instance.
Table 5: Fuzzy Temporal Database Instance.
NAME ID . . . EXP. FVP
GRANT 1245 TRAINEE (15/06/1997, 31/05/1998, 2,2)
GRANT 1245 JUNIOR (02/06/1998, 31/12/2050,2,0)
REDFORD 9877 TRAINEE (20/08/1994, 31/01/1996, 2,3)
REDFORD 9877 JUNIOR (03/02/1996, 31/03/1997,3,4)
REDFORD 9877 SENIOR (04/04/1997, 31/12/2050,4,0)
BROWN 1278 JUNIOR (01/05/1996,10/08/97,0,0)
STREEP 6579 TRAINEE (15/06/1997,31/12/2050,0,0)
NEWMAN 5546 SENIOR (18/06/1997,29/04/1998,8,10)
4.1 Queries about a Precise Date
In this case, QT is a date d and the system must find
the tuples whose FVP includes d in the support set,
that is, those tuples for which the membership of this
date to the fuzzy period is greater than 0. Once found,
the fulfillment degree of the resulting tuple will be
computed as:
µ
FV P
(d)
It should be noted that this degree will be 1 when
the date d belongs to the modal set of the fuzzy inter-
val.
As explained before, it may happen that not only
one but two versions of the same tuple have a validity
period that includes d in the support set. This is the
case when the mentioned date belongs to the closing
interval of two consecutive periods. In this case, the
answer will be the tuple whose fulfillment degree is:
⊕(µ
FV P1
(d), µ
FV P2
(d))
i.e. the one whose validity time best fits the query
date. The fuzzy set theory provides many different
operators that may be chosen depending on the de-
sired effect. For example, in this case we could use
the maximum.
One example of this type of query is Find the ex-
pertise level of employee number 9877 on 1st April
1997. This situation can be graphically seen in figure
6 and the formal expression of this query using FSQL
syntax is:
fsql> SELECT empnam,expertise,CDEG(fvp)
FROM employees
WHERE empid=9877 AND
fvp FEQ TO_DATE(’01/04/1997’) THOLD 0.0;
NAME EXP. FVP CDEG(FVP)
------------------------------------------------
REDFORD JUNIOR (03-02-1996,31-03-1997,3,4) 0.75
REDFORD SENIOR (04-04-1997,31/12/2050,4,0) 0.25
03/02/9631/01/96
1
Days
31/12/2050
04/04/97
µFVP1(x)
31/03/97
µFVP2(x)
d
0.75
0.25
Figure 6: Membership degrees when date d belongs to the
closing interval of two tuples.
4.2 Queries about a Fuzzy Period of
Time
In this case, QT is another fuzzy interval of dates and
the system should find the tuples whose FVP includes
FUZZY TIME REPRESENTATION AND HANDLING IN A RELATIONAL DB
95

QT and compute to what degree this inclusion is ful-
filled. This situation can be modelled by means of the
implication:
QT −→ FV P
If we assume that the implication function
I(QT (d), FV P(d)) used is the material implication,
then the fulfillment degree of this fuzzy inclusion will
be:
N(FV P|QT ) = min
x∈D
I(µ
QT
(x),µFV P(x))
N(FV P|QT ) = min
x∈D
{(1 − µ
QT
(x)) ⊕ µ
FV P
(x)}
If the t-conorm considered is the maximum, the
resulting measure is a necessity. Note that this mea-
sure includes the classical sets inclusion as a particu-
lar case.
If more than one version of a tuple give a positive
result for the inclusion degree, then the best answer
will be the one with the highest degree.
One example of this type of query is Find the boss
of employee number 9877 by the beginning of April
1997 (01/04/97,05/04/97,0,2). The formal expression
of this query using FSQL syntax is:
fsql> SELECT e.empnam, e.expertise, e.boss,
CDEG(e.fvp)
FROM employees WHERE e.empid=9877 AND
$[’01/04/1997’,’05/04/1997’,0,2] NFEQ fvp
THOLD 0.0;
NAME EXP. BOSS CDEG(FVP)
-----------------------------
REDFORD SENIOR 9989 0,25
where
NFEQ
(necessity-based fuzzy equal) com-
putes to what degree the left side fuzzy set is included
in the right side one using the expression given above.
4.3 Simultaneous Events
The problem now is to compute to what degree two
events are simultaneous. This operation is very useful
since joins are based on it. The simultaneity degree
or temporal equality between two periods of time can
be carried out computing the degree to which both
fuzzy/crisp sets -FV P
1
and FV P
2
- are mutually in-
cluded one in the other, that is, we should compute:
⊗{N(FV P
1
/FV P
2
),N(FV P
2
/FV P
1
)}
as the final value for the fuzzy equality degree be-
tween the two fuzzy sets where ⊗ stands for a T-norm
(minimum is our case).
A query of this type could be Find employees with
the boss 9877 during the same period of time. The
formal expression of this query using FSQL syntax
is:
fsql> SELECT e.empnam,f.empnam,CDEG(*)
FROM employees e, employees f
WHERE e.boss=9877 AND f.boss=9877
AND e.empid<>f.empid
AND (f.fvp NFEQ e.fvp) >0
AND (e.fvp NFEQ f.fvp) >0
E.EMPNAM F.EMPNAM CDEG(*)
---------------------------
GRANT NEWMAN 0,4
where
CDEG(*)
computes the minimum of the fulfill-
ment degrees obtained.
5 CONCLUSIONS AND FUTURE
WORK
In this paper we have shown the advantages of repre-
senting fuzzy temporal data with a parametrical rep-
resentation. On this temporal data, we have explained
how an update operation can be carried out by taking
into account that no deletion is possible when tempo-
ral information is stored. As a result of this opera-
tion, a modification to the old version of the tuple is
needed by changing some of the parameters that de-
fine it. As a consequence of our approach, the queries
return a set of tuples together with a fulfillment degree
when a query is made on these fuzzy temporal data.
The paper also analyzes the different types of queries
that can be made on these data. We are currently ana-
lyzing the behavior of other operators (after, before,
short time, long time ago, etc.) and considering a
wider range of temporal data. We are also studying
the problem of primary keys in the presence of fuzzy
intervals instead of VST and VET attributes and try-
ing to find out new indexing techniques that take the
new primary keys into account.
ACKNOWLEDGEMENTS
This work has been partially supported by research
projects TIC1570 and P07-TIC-03175 of the Spanish
Junta de Andaluca.
ICSOFT 2008 - International Conference on Software and Data Technologies
96

REFERENCES
C. Bettini, X. Wang, S. Jajodia. A general framework for
time granularities and its application to temporal rea-
soning. Annals of Mathematics and Artificial Intelli-
gence, vol. 22, pp.29-58. (1998)
R. de Caluwe, G. de Tr, G. Bordogna. (Eds.) Spatio-
Temporal Databases Flexible Querying and Reason-
ing. ISBN: 978-3-540-22214-9 (2004).
P. Chountas, I. Petrounias Modeling and Representation of
Uncertain Temporal Information. Requirements Eng.
5, pp. 144-156 (2005).
Dubois D., Prade H. Fuzzy Numbers. An Overview. The
Analysis of Fuzzy Information. Bezdek Ed. CRS
Press, Boca Raton. (1985)
R. Elmarsi, G. T. Wuu A Temporal Model and Query Lan-
guage for ER Databases. (1990)
O. Etzion, S.Jajodia, S. Sripada (Eds.) Temporal Databases;
Research and Practice. Lecture Notes in Computer
Science, vol. 1399. Springer. (1998).
J. Galindo, J. M. Medina, O. Pons, J. C. Cubero A Server for
Fuzzy SQL Queries. T. Andreasen, H. Christiansen,
and H.L. Larsen (Eds.). FQAS’98, LNAI 1495, pp.
164-174. (1998).
J. Galindo, A. Urrutia, M. Piattini Fuzzy Databases: Mod-
eling, Design and Implementation. Idea Group Pub-
lishing, Hershey, USA. (2006).
Goguen, J. A. L-Fuzzy Sets. Journ. of Math. Anal. and Ap-
plications, vol. 18, pp. 145-174. (1967)
J. M. Medina, O. Pons, M. A. Vila GEFRED: A General-
ized Model of Fuzzy Relational Databases. Informa-
tion Sciences, vol. 76, pp. 87-109.(1994)
J. M. Medina, J. C. Cubero, O. Pons, M. A. Vila Towards
the Implementation of a Generalized Fuzzy Relational
Database Model. Fuzzy Sets and Systems, vol. 75, pp.
273-289. (1995)
R. T. Snodgrass (ed.), I Ahn, G. Ariav, D. S. Batory, et. Al
The TSQL2 temporal query language. Kluwer Aca-
demic (1995).
A. Tansel, J. Clifford, S. Gadia. Temporal Databases: The-
ory, Design and Implementation. Bejamin Cummings
(1993).
B. Van der Cruyssen, R. de Caluwe, G. de Tre. A Theo-
retical Time Model for Dealing with Crisp and Fuzzy
Time. Proceeings of NAFIPS. (1997).
FUZZY TIME REPRESENTATION AND HANDLING IN A RELATIONAL DB
97
