COMPRESSED DATABASE STRUCTURE TO MANAGE LARGE
SCALE DATA IN A DISTRIBUTED ENVIRONMENT
B. M. Monjurul Alom, Frans Henskens and Michael Hannaford
School of Electrical Engineering & Computer Science, University of Newcastle , Callaghan, NSW 2308, Australia
Keywords: Compression, Single Column, Fragment, Single Vector, Cardinality.
Abstract: Loss-less data compression is attractive in database systems as it may facilitate query performance
improvement and storage reduction. Although there are many compression techniques which handle the
whole database in main memory, problems arise when the amount of data increases gradually over time, and
also when the data has high cardinality. Management of a rapidly evolving large volume of data in a
scalable way is very challenging. This paper describes a disk based single vector large data cardinality
approach, incorporating data compression in a distributed environment. The approach provides substantial
storage performance improvement compared to other high performance database systems. The compressed
database structure presented provides direct addressability in a distributed environment, thereby reducing
retrieval latency when handling large volumes of data.
1 INTRODUCTION
In main memory database systems data resides
permanently in main physical memory, whereas in a
conventional database system it may be disk resident
(Garcia-Molina and Salem 1992). Conventional
database systems cache data in main memory for
access; in main memory database systems data may
have a backup copy on disk. In both cases,
therefore, a given object can have copies both in
memory and on disk. The key difference is that in
main memory databases the primary copy lives
permanently in memory. Main memory is normally
directly accessible and volatile while disks are not.
The layout of data on a disk is much more critical
than the layout of data in main memory, since
sequential access to a disk is faster than random
access (Garcia-Molina and Salem 1992). The main
pitfall of main memory databases is that they cannot
handle very large amounts of data because they are
fully dependent on main memory. This can be
alleviated somewhat, for example the HIBASE
compression technique (Cockshott, Mcgregor et al.
1998) is main memory based and applicable to low
cardinality of domain values. In this paper we
present a single vector large data cardinality
structure (SVLDCS) that is disk based and supports
large databases as well as high cardinality of domain
values with the facility to access compressed data in
distributed environments. Portions of the
compressed database structure are available in main
memory on the basis of the query demand from
different sites. The main copy of the domain
dictionary is stored permanently on the disk and a
back up copy is available in the main memory. This
structure is used to handle large scale of tuples and
attributes while providing a level of storage
performance comparable to conventional database
systems. This structure may be easily used in areas
where database is often typically only, for example
for analytical processing, data warehousing and data
mining applications.
The remainder of this paper is organized as follows:
Related work is described in section 2. The existing
HIBASE method is presented in section 2.1 - our
method is an extension of this architecture. The
(SVLDCS) single vector large data cardinality
structure is described in 3. Section 4 and 5 present
the search technique and analysis of storage capacity
respectively. The paper concludes with a discussion
and final remarks in section 6.
2 RELATED WORK
The HIBASE architecture (Cockshott, Mcgregor et
al. 1998) defines a way of representing a dictionary
based compression technique for relational databases
37
M. Monjurul Alom B., Henskens F. and Hannaford M. (2008).
COMPRESSED DATABASE STRUCTURE TO MANAGE LARGE SCALE DATA IN A DISTRIBUTED ENVIRONMENT.
In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 37-44
DOI: 10.5220/0001875600370044
Copyright
c
 SciTePress

that are fully main memory based. This structure is
designed for low cardinality of the domain
dictionaries, with an architecture that replaces code
rather than the original data values in tuples. The
main pitfall of this method is that the structure
cannot handle large databases because of full
dependency on main memory in combination with
the limitations of large memory spaces.
Investigation of main memory database systems is
well described in (Garcia-Molina and Salem 1992),
with a major focus on fidelity of main memory
content compared to conventional disk based
database systems. Memory resident database
systems (MMDB’s) store their data in main physical
memory, providing high data access speeds and
direct accessibility. As semiconductor memory
becomes less expensive, it is increasingly feasible to
store databases in main memory and for MMDB’s to
become a reality.
The unique graph-based data structure called
DBGraph may be used as a database representation
tool that fully exploits the direct access capability of
main memory. Additionally, the rapidly decreasing
cost of RAM makes main memory database systems
a cost effective solution to high performance data
management (Pucheral, Thevnin et al. 1990). This
overcomes the problem that disk-based database
systems have their performance limited by I/O.
A compressed 1-ary vertical representation is
used to represent high dimensional sparsely
populated data where database size grows linearly
(Hoque 2002). Queries can be processed on the
compressed form without decompression;
decompression is done only when the result is
necessary. Different kinds of problem, such as
access control and transaction management, may
apply to distributed and replicated data in distributed
database systems (DDBMS) (Alkhatib and Labban
1995). Oracle, a leading commercial DBMS,
defines a way to maintain consistent state for the
database using a distributed two phase commit
protocol. (Alkhatib and Labban 1995) address some
issues such as advantage, disadvantage, and system
failure in distributed database systems. Since
organizations tend to be geographically dispersed, a
DDMBS fits the organizational structure better than
traditional centralized DBMS. Advantages of
DDBMS include that failure of a server at one site
will not necessarily render the distributed database
system inaccessible. A general architecture for
archiving and retrieving real-time, scientific data is
described in (Lawrence and Kruger 2005). The
basis of the architecture is a data warehouse that
stores metadata on the raw data to allow for its
efficient retrieval. A transparent data distribution
system uses the data warehouse to dynamically
distribute the data across multiple machines.
A single dictionary based compression technique
to manage large scale databases is described by
Oracle corporation (Poess and Potapov 2003). The
authors also address an innovative table compression
technique that is very attractive for large relational
data warehouses. This technique is used to
compress and partition tables. The status of a table
can be changed from compressed to non-compressed
at any time by simply adding the keyword
COMPRESS to the table’s meta-data.
The LH*
RS
scheme defines a way of storing
available distributed data (Litwin, Moussa et al.
2004). This system includes distributed data
structures [SDDS] that are intended for computers
over fast networks, usually local networks. This
architecture is a promising way to store distributed
data and gaining in popularity.
A distributed storage system for structured data
called Bigtable is presented in (Chang, Dean et al.
2006). The system is used for managing data that is
designed to scale to very large size datasets
distributed across thousands of commodity servers.
Bigtable has successfully provided a flexible, high
performance solution for all of the Google products.
2.1 Existing HIBASE Compression
Technique
The basic HIBASE model, as described in
(Cockshott, Mcgregor et al. 1998), represents tables
as a set of columns (rather than as a set of rows as
used in a traditional relational database). This
structure is dictionary based, and designed for low
cardinality of domain values. The architecture
replaces code rather than the original data values, in
tuples. The main pitfall of this method is that it
cannot handle large databases because of its fully
main memory dependency. HIBASE uses single
block column vector; each attribute is associated
with a domain dictionary and a column vector. The
columns are organized as a linked list, each of which
points into the dictionary. Figure 1 shows a
HIBASE structure together with its domain
dictionary. There are 7 distinct lastnames
represented by identifiers numbered 0 to 6 which
can be represented by 3 bits; similarly suburb, state
and marital status are represented by 2, 1 and 1 bits
respectively. Hence, in compressed representation
7 bits are required to represent one tuple using the
HIBASE method. For the set of 8 tuples, 56 bits
would be required. In the uncompressed relation
ICSOFT 2008 - International Conference on Software and Data Technologies
38

(Figure 1) an average of 10 bits are required for each
attribute, totalling 40 bits for each tuple, hence the
total uncompressed relation requires 320 bits for all
tuples. The HIBASE approach thus appears to
achieve a huge compression ratio; in fact the overall
compression is somewhat less impressive because
representing the domain dictionary requires some
memory space.
Figure 1: Compressed relation with domain dictionary.
3 PROPOSED SINGLE VECTOR
LARGE DATA CARDINALITY
(SVLDCS) STRUCTURE
The single vector large data cardinality structure
(SVLDCS) is disk based, supports large data
cardinality of domain dictionaries, and can used in a
distributed environment. In this structure an
Attribute_Bit_Storing dictionary is used to store the
length of the required bit sequence for each attribute.
This system generates a serial number for each tuple
in the original relational table, and does not provide
lineation of columns for different attributes as seen
in the HIBASE method.
The (possibly huge amount of) information in a
relational table is stored in compressed form with
partitioning the attributes into different blocks. In
each tuple of the compressed relation there may be a
different number of blocks, and it is possible to store
the information of a large number of attributes in
each block. Each of the database fragments can
accommodate 2
32
tuples. Searching techniques can
be applied to this compressed database format, and
the actual information then retrieved from the
domain dictionary. As the database gradually
increases, the domain dictionaries can be partitioned
so there is one (active) part in main memory and
other (inactive) parts in permanent storage. A single
vector is used to point each of the database
fragments.
When the number of tuples and attributes
gradually increase, the single vector continues to be
sufficient to handle this large data cardinality. The
vector represents a collection of different fragments
with multiple blocks and a large number of tuples.
Any fragment of the compressed database can be
distributed into any of the sites of the distributed
environment, and a copy of the whole compressed
database can be stored on disk.
Among the set of fragments there will at any
time be a limited number of fragments in main
memory. To satisfy query demand, other fragments
may need to become available in main memory.
New search key values (lexeme) are always inserted
at the end of the domain dictionary. Encoding is
performed before inserting the lexeme to make sure
the lexeme is not redundant. The Id of the search
key values are retrieved from original database
relation before starting query, after which the query
results are found from the domain dictionary. In
Figure 1, all the information is compressed using
binary values in the domain (columns) (Cockshott,
Mcgregor et al. 1998). The SVLDCS approach
represents this same information using a single
columnar block as shown in Figure 2. When the
number of attributes and tuples increases, the
SVLDCS structure is capable of representing this
information using multiple blocks and compressed
fragments are pointed to by a single vector.
Last
Name
Suburb State Marital
Status
Michael Lambton NSW Marrie
d
Ste
p
hen Lam
p
ton Victoria Unmarrie
d
Alex Hamilton NSW Marrie
d
Drew Jesmon
d
NSW Marrie
d
Frans Lambton Victoria Marrie
d
Lin Lambton NSW Marrie
d
Davi
d
Jesmon
d
Victoria Marrie
d
Alex Jesmon
d
NSW Unmarrie
d
Id Last
Name
Suburb State Marital
Status
0 Michael Lambto NSW Marrie
d
1 Ste
p
hen Hamilto Victoria Unmarrie
d
2 Alex Jesmon
d
3 Drew
4 Frans
5 Lin
6 Davi
d
0
(
000
)
0
(
00
)
0 0
1
(
001
)
0
(
00
)
1 1
2
(
010
)
1
(
01
)
0 0
3
(
011
)
2
(
10
)
0 0
4
(
100
)
0
(
00
)
1 0
5
(
101
)
0
(
00
)
0 0
6
(
110
)
2
(
10
)
1 0
2
(
10
)
2
(
10
)
0 1
Compression Engine
Com
p
ressed Relation
Original Relation
Domain Dictionar
y
COMPRESSED DATABASE STRUCTURE TO MANAGE LARGE SCALE DATA IN A DISTRIBUTED
ENVIRONMENT
39

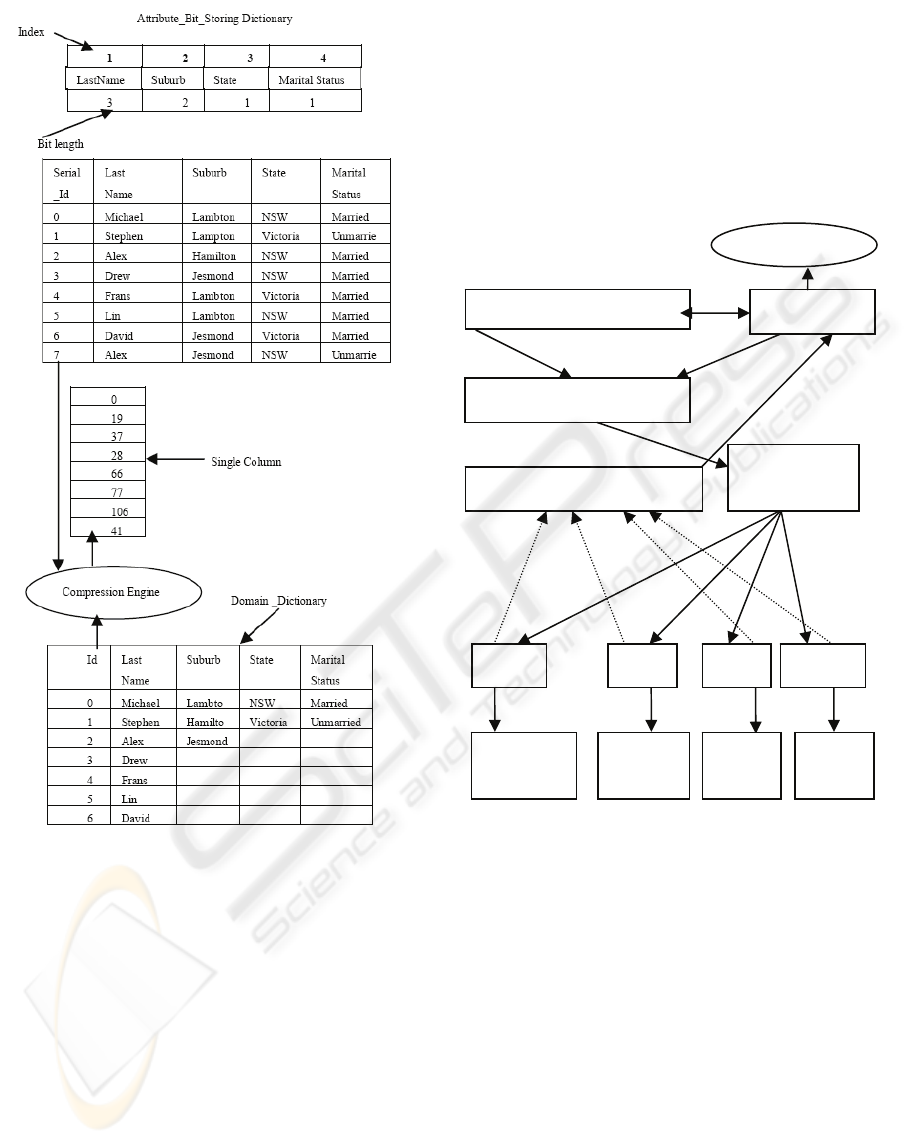
Figure 2: Compressed structure using single block.
The structure as used in a distributed environment is
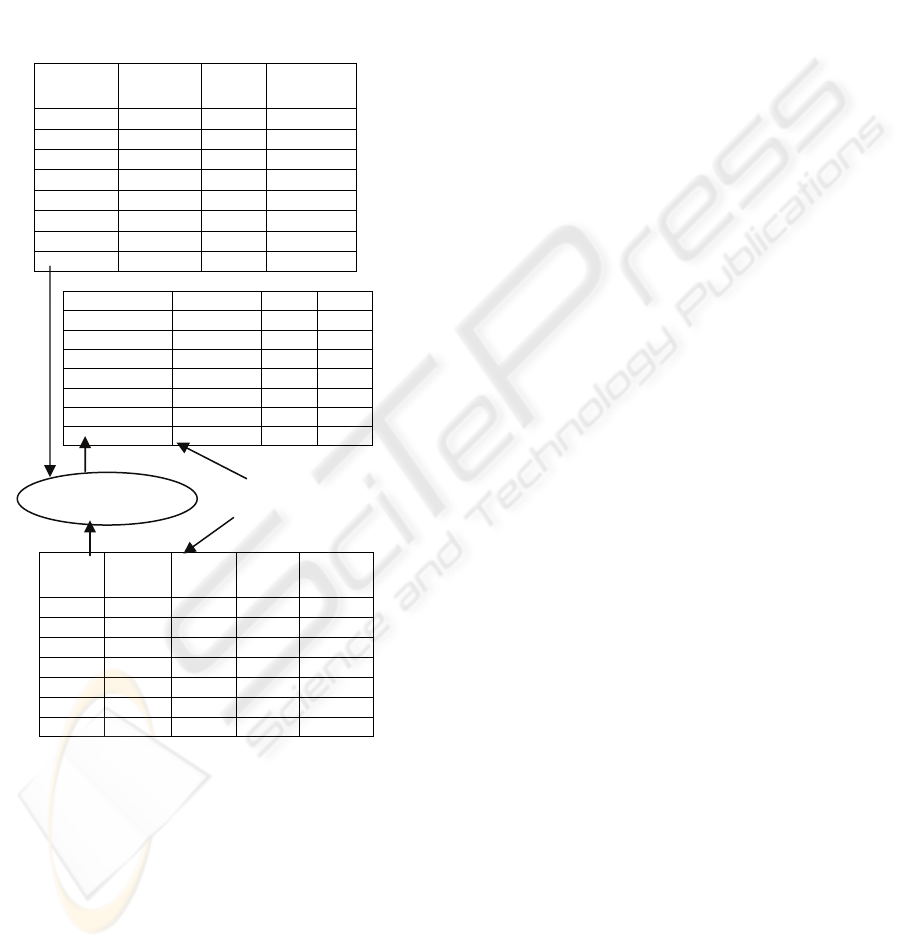
given in Figure 3. The SVLDCS data structure is
represented in Figure 4. Each fragment can consist
of up to 2
32
tuples, and each block can hold up to 32
bits of information. While only 4 blocks are
presented in Figure 4, the same arrangement may be
used to handle more blocks as well as a larger
number of attributes. In Figure 4, the single vector
structure points to each compressed database
fragment, each of which in turn is used to hold the
information of a large number of tuples.
4 SEARCHING TECHNIQUE
The algorithm as described in Figure 5 is used to
handle large amounts of data using a single vector
consisting of multiple fragments with multiple
blocks. This algorithm is used to search the large
data cardinality structure. To understand the
algorithm the following data structures are
necessary:
Figure 3: Overall Structure of SVLDCS in distributed
environment.
Data Structure:
AttributeBitStoring[]: Stores the required bit length
for each attribute of the relation.
Lexeme: Value of the search key attribute.
Token: The Id of the encoded lexeme; retrieved
lexeme: desired key (lexeme) values.
Domain_dictionary [ ] [ ]: Stores the distinct tuples
for each attribute with token value.
Compressed_Data[ ]: Stores the results in
compressed format.
Vector_index: Points to each fragment of the
compressed database.
Single_vector [ ]: Stores the index of a vector up to
n; where n= total number of tuples in main relation /
2
32
.
Multi Block Compressed Database
Database Coordinator
Data Fragmentation
Engine
Site
1
Site
2
Compressed
database
Original Database in Disk Domain dictionary
Output
…. Site
n
Compressed
database
Compresse
d database
Compresse
d database
ICSOFT 2008 - International Conference on Software and Data Technologies
40

Y[]: Array that stores all the compressed decimal
values of specific tuple from a specific fragment.
X[]: Array used to store the binary representation of
the decimal value that is stored in Y.
Single Column: Used to store the information of the
relation when the number of tuples and attributes are
not on a large scale.
Figure 4: Single vector structure with multi block
compressed data representation.
Algorithm Search_SVLDCS()
Begin
Search the serial_Id for the given
lexeme from main database relation;
Vector_Index= Serial_Id of the given
lexeme/ 2
32
;
//Accessing the values of multiple
//block from the specific tuple of
//specific fragment
For (i=0 to p-1 Block do)
Begin
// where p (total blocks)=
//maximum bit length of the tuple
//of main relation/32;
Y[i]=Single_vector[vector_index]->
compressed_data[serial_Id][i];
End;
//retrieving the compressed value
from //single columnar vector table;
X= X
1
X
2
…….X
n
=Int_to_Binary [Yi …..Yp];
Retrieved_lexeme=Domain_dictionary[sou
rce][tagret];
Where target= the index number of
target (output)attribute from
Attribute_Bit_Storing Dictionary;
first_bit_length= ∑ Bit length (from
starting bit length to length of
query attribute from
Attribute_Bit_Storing Dictionary);
source=Converted decimal value of
X[],from position of the
first_bit_length to number of bit
length of query attribute;
If( retrieved_lexeme ) return 1;
//Value found
Else return 0;
// or search for another input;
End. // End of Main
.
Figure 5: Algorithm Single vector Structure for large
compressed database.
4.1 Explanation of the Searching
Technique of (SVLDCS) Structure
Consider the original relation given in Figure 1,
Attribute_Bit_Storing Dictionary,
Domain_dictionary, and Single_Column as given in
Figure 2, suppose it is required to find the State
information of LastName= Drew. The system finds
the Serial Id of the lexeme (LastName from original
relation), which is 3. The value of that index (Serial
Id) position from Single_Column is 28.
So Y=Single_Column [3] = 28. The converted
binary value of Y is stored in X. Thus
X=X
0
…..X
6
=Int_to_Binary (Y) =0011100 (as the
length bit is 7).
Retrieved_lexeme (Value of State) =
Domain_Dictionary [source] [target], where target =
the index number of the (State) attribute from
Attribute_Bit_Storing_Dictionary=3
source=Converted decimal value of X [ ], from
position of the first_bit_length to the number of bit
length of retrieved_lexeme.
Where first_bit_length= ∑ Bit length (From the
starting bit length upto the length of retrieved
lexeme (from Attribute_Bit_Storing Dictionary)).
Firstbitlength=3+2=5 and length of the attribute
state is 1.
Source= Converted decimal value of X [ ] [From
the 5
th
position to 5
th
position, as length of attribute
state is 1)=Bin_to_Decimal (0)=0
Retrieved_lexeme (Value of State) = Domain
Dictionary [source] [target] = Domain_Dictionary
[0] [3]= NSW. We see the value of the retrieved
lexeme (State) =NSW which is also the same in the
original database relation. Similarly this technique
is applied to the large number of tuples with multiple
fragments and attributes divided into blocks
according to the given algorithm in Figure 5. In
Figure 4, the information for a large number of
attributes and tuples are presented, providing
multiple fragments and blocks with a single vector.
B
1
B
2
B
3
B
4……
0…. 31 32…… 63 64 95 96 127
Bloc
k
Compressed_Data
Vecto
r
0
….
.…
n
….. 1234422 234156 5678754 2345
….. 409000000 1290900 10987650 9098
…. ………..... ……….. ………… ……
….. …………. ……….. ………… ……
n
-tuple
858993459 ………. ……….. ……
0 1234422 23415 5678754 2345678
1 409000000 12909 1098765 9098772
2 ………..... …… ……… ……….
… …………. …… ……… ………..
…. ………….. …… ……… ………..
2
32
-1
429006600 …… ……….. ……….
Fragment
n
Fragment
1
COMPRESSED DATABASE STRUCTURE TO MANAGE LARGE SCALE DATA IN A DISTRIBUTED
ENVIRONMENT
41

4.2 Searching Time Analysis of Our
SVLDC Structure
The total search time of SVLDC structure is
(
SVLD
T ) = (Time taken to search the lexeme Id from
original relation + Domain Dictionary searching +
Compressed_Data searching from Single vector):
SVLD
T =
CDDDLOR
TTT ++ (1)
In a compressed_data search from a single
vector, a hashing technique is applied to find the
vector index as well as fragment location (given as
fragment_no=hash (serial_id_lexeme)/2
32
). So the
compressed_data searching time is:
CD
T =
)1(Ο
(2)
In the domain dictionary only the value of the
particular attributes are retrieved during a search of
the structure. Therefore the search time of the
domain dictionary is constant. To insert a new tuple
in the database, the domain dictionary would be
searched to make sure of its existence in the
database; if the lexeme is not found in the domain
dictionary, the new lexeme is inserted at the end of
the domain dictionary and a token is created for that
lexeme. So
D
T
= )1(Ο + )(nΟ (3)
where n is the total number of tuples in the domain
dictionary. To find out the Serial_Id of the lexeme
from the main relation the required time would be:
LOR
T = Ο (
n
n
2
log*
+
n
2
log
) (4)
A binary search technique may be applied to find
any lexeme’s serial Id and it would take
Ο
(
n
2
log
) time, where n is the total number of
tuples. Before applying a binary search technique, it
is required to sort the relation according to any
specific attribute, and that takes O (
n
n
2
log*
)
time.
5 THE ANALYSIS OF STORAGE
CAPACITY OF SVLDC
STRUCTURE
The required memory for each Compressed Data
fragment is:
CF
S = )**(
∑
bpm (5)
Where m= maximum_no_of tuples of a
fragment=2
32
; p=no_of_block_per_tuple;
b=avg_bytes_required_each_block; n= Total no of
tuples in main relation /m; Fragment_tuple= Total
no of tuple in main relation % m;
When (Fragment_tuple) =0, this represents that
every fragment in a single vector is filled up with the
maximum number of tuples.
Hence the required memory for a Single Vector
is:
SV
S =
∑
=
n
j
CF
S
1
)( (6)
The required memory for the Domain Dictionary
is:
DD
S
=
∑
=
q
i
LC
1
)*(
(7)
where q is the total number of tuples in domain
dictionary, C is the number of attributes, L is the
average length of each attribute. Combining
equation (6) and (7) the total required memory for
SVLDCS is:
SVLDC
S =
SV
S +
DD
S (8)
When (Fragment_tuple) is not zero, this
indicates that all the fragments are not filled by the
maximum number of tuples. It is convention that
the last fragment has tuples that are less than the
maximum number of tuples. In that case the
required memory is:
SVLDC
S =
∑
=
n
j
CF
S
1
)([ +
DD
S + ]
NF
S (9)
where
NF
S =fragment_tuple*no_of_blocks_per_tupl
e*bytes_required_for_each_block.
5.1 Analytical Analysis of Storage
Capacity using Different Methods
Let CF be the compression factor,
Storage
UR be
the required storage for uncompressed relation,
Storage
CRV be the storage capacity for compressed
relation in SVLDCS,
DD
S
be the domain dictionary
storage capacity. The compression factor is
represented by
CF = )(
DDstoragestorage
SCRVUR + (10)
ICSOFT 2008 - International Conference on Software and Data Technologies
42

It is estimated that if the dictionary takes 25% of
total storage, then
DD
S = .25
Storage
UR ;
Storage
CRV = .75
Storage
UR ;
So,
DD
S /
Storage
CRV = .25/.75 =.33;
DD
S =.33*
Storage
CRV (11)
Combining (10) and (11) we have
CF =
storagestorage
CRVUR *33.1
Storage
UR = CF *
storage
CRV*33.1 (12)
Oracle data compression (Poess and Potapov 2003)
achieves the average compression factor
orc
CF =3.11. The total storage required in the
Oracle compression technique:
Storage
ORC :
= the required storage for uncompressed data /
Compression factor
Storage
ORC =
Storage
UR / CF
orc;
Using equation (12) we have:
Storage
ORC = CF *
storage
CRV*33.1 / 11.3
Storage
ORC = CF *
storage
CRV*43. (13)
In (Lawrence and Kruger 2005) the Tera-scale
architecture is described on a Dual processor,
achieving a data rate in compressed form of
3GB/day, whereas uncompressed data stream is
about 15GB/day, so compression (
tera
CF ) factor is
about 5. So the storage capacity for Tera-scale is:
storage
Tera =
Storage
UR /
tera
CF ;
Using equation (12) we have
storage
Tera =
storage
CRVCF *33.1* / 5 ;
storage
Tera =
*596.1
Storage
CRV (14)
A graphical representation of memory
requirements of uncompressed database, SVLDCS,
compressed database in Oracle (Poess and Potapov
2003) and compressed database in Tera-scale
(Lawrence and Kruger 2005) structure are presented
in Figure 6. It is clear that the storage size of
databases increases due to increase in the number of
tuples. The number of tuples (in million) are
represented by the X axis and the storage capacity
(in Tera Bytes) of different methods are represented
by the Y axis. The storage comparison is also
presented in a tabular form (in Table 1) for different
methods using equation (8), (9),(12), (13) and (14).
Table 1: Required Memory (in Terabytes) Using Different
Methods.
Note that Oracle (Poess and Potapov 2003) and
Tera-Scale ((Lawrence and Kruger 2005) requires
710 GB and 440 GB respectively while SVLDCS
reduces these significantly to only 275 GB. From
Table 1, we see the compression factor is almost 8:1,
comparing uncompressed to compressed relation
(SVLDCS). After considering the domain
dictionary (using equation (12)), this compression
factor becomes 6:1.
Figure 6: Comparison of Storage Space for Different
Methods.
6 CONCLUSIONS
Management and processing of large scale data sets
is time-consuming, costly and an obstruction to
research. Accessing a rapidly evolving large scale
database in a concurrent environment is also
challenging because the number of disk accesses
increases as the database size grows; the response
No_of
Tuples
million
Uncomp
ressed
(TB)
ORACLE
(TB)
TERA-
SCALE
(TB)
SVLDCS
(TB)
759 0.1875 0.059 0.037 0.023
1215 0.3 0.096 0.06 0.0375
1620 0.4 0.129 0.08 0.05
2025 0.5 0.161 0.1 0.0626
3038 0.75 0.239 0.15 0.093
3443 0.85 0.273 0.17 0.106
3848 0.95 0.307 0.19 0.119
4172 1.03 0.335 0.207 0.13
5388 1.33 0.43 0.266 0.167
8600 2. 20 0.71 0.44 0.275
COMPRESSED DATABASE STRUCTURE TO MANAGE LARGE SCALE DATA IN A DISTRIBUTED
ENVIRONMENT
43

time of any query also increases. This paper
describes an innovative disk based single vector
large data cardinality approach, incorporating data
compression in a distributed environment.
According to this technique data are stored in a more
space-efficient way than is provided by other
existing schemes such as HIBASE, Oracle and Tera-
scale. The compressed structure of SVLDCS is
better than compression in Oracle, because Oracle
applies block level compression that includes some
redundancy. The Tera-scale architecture also
compress data file but querying is not possible when
the data is in compressed form. When the SVLDC
approach is applied to a database of 2.2 TB (tera
bytes), only 275 GB of storage is required, a
significant improvement over other schemes. The
compression factor achieved using the SVLDCS
structure is 6:1 compared to uncompressed relation.
Querying, updating, inserting, deleting, and
searching data in the databases is supported by the
SVLDCS technique; details of these will be further
reported as research progresses.
REFERENCES
Agrawl, R., A. Somani, et al., 2001. Storage and Querying
of E-commerce Data. The 27th International
Conference on Very Large Databases(VLDB). Roma,
Italy.
Alkhatib, G. and R. S. Labban., 1995. "Transaction
Management in Distributed Database Systems: the
Case of Oracle’s Two-Phase Commit." The Journal of
Information Systems Education 13:2: 95-103.
Chang, F., J. Dean, et al., 2006. Bigtable: A Distributed
Storage System for Structured Data. The International
Conference on Operating Systems Design and
Implementation (OSDI). Seattle, Wa, USA.
Cockshott, W. P., D. Mcgregor, et al., 1998. "High-
Performance Operations Using a Compressed
Database Architecture”. The Computer Journal 41:5:
283-296.
Garcia-Molina, H. and K. Salem., 1992. "Main Memory
Database Systems: An Overview " IEEE Transaction
on Knowledge and Data Engineering 4:6: 509-516.
Hoque, A. S. M. L., 2002. Storage and Querying of High
Dimensional Sparsely Populated Data in Compressed
Representation. Euro-Asia ICT. LNCS 2510.
Hoque, A. S. M. l., D. McGregor, et al., 2002. Database
compression using an off-line dictionary method. The
Second International Conference on Advances in
Information Systems (ADVIS). LNCS 2457, Springer
Verlag Berlin Heidelberg.
Lawrence, R. and A. Kruger., 2005. An Architecture for
Real-T'ime Warehousing of Scientific Data. The
International Conference on Scientific Computing
(ICSC). Vegus, Nevada.
Lawrence, R. and A. Kruger., 2005. An Architecture for
Real-Time Warehousing of Scientific Data. The
International Conference on Scientific Computing
(ICSC). Vegus, Nevada, USA.
Lee, I., H. Y. Yeom, et al., 2004. "A New Approach for
Distributed Main Memory Database Systems: A
Casual Commit Protocol." IEICE Trans. Inf. & Syst.
87:1 196-204.
Lehman, T. J., E. J. Shekita, et al., 1992. "An Evaluation
of Starburst’s Memory Resident Storage Component."
IEEE Transaction on Knowledge and Data
Engineering: 555-566.
Litwin, W., R. Moussa, et al. (2004). LH*RS: A Highly
Available Distributed Data Storage The 30th
International Conference on Very Large Databases
Conference. Toronto, Canada.
Poess, M. and D. Potapov., 2003. Data Compression in
Oracle. The 29th International Conference on Very
Large Databases(VLDB), Berlin, Germany.
Pucheral, P., J.-M. Thevenin, et al., 1990. Efficient Main
Memory Data Management using DBGraph Storage
Model. The 16th International Conference on Very
Large Databases(VLDB). Brisbase, Australia.
Simonds, L., 2005. A Terabyte for your Desktop. The
Maxtor Corporation Technical Report.
Stonebraker, M., D. J. Abadi, et al., 2005. C-Store: A
Column-Oriented DBMS. The 31st International
Conference on very Large Dtabases (VLDB).
Trondheim, Norway.
Thakar, A., A. Szalay, et al., 2003. "Migrating a Multi-
Terabyte Archive from Object to Relational Databas."
The Journal of Computing Science and Engineering
5:5 16-29.
ICSOFT 2008 - International Conference on Software and Data Technologies
44