STRATEGIES FOR OPTIMIZING QUERYING THIRD PARTY
RESOURCES IN SEMANTIC WEB APPLICATIONS
Albert Weichselbraun
Institute for Information Business, Vienna University of Economics and Business Administration, Vienna, Austria
Keywords:
Search-test-stop, query optimization, Web services.
Abstract:
One key property of the Semantic Web is its support for interoperability. Combining knowledge sources from
different authors and locations yields refined and better results.
Current Semantic Web applications only use a limited amount of particularly useful and popular information
providers like Swoogle, geonames, etc. for their queries. As more and more applications facilitating Semantic
Web technologies emerge, the load caused by these applications is expected to grow, requiring more efficient
ways for querying external resources.
This research suggests an approach for query optimization based on ideas originally proposed by McQueen
for optimal stopping in business economics. Applications querying external resources are modeled as deci-
sion makers looking for optimal action/answer sets, facing search costs for acquiring information, test costs
for checking the acquired information, and receiving a reward depending on the usefulness of the proposed
solution.
Applying these concepts to the information system domain yields strategies for optimizing queries to external
services. An extensive evaluation compares these strategies to a conventional coverage based approach, based
on real world response times taken from three different popular Web services.
1 INTRODUCTION
Semantic Web applications provide, integrate and
process data from multiple data sources including
third party providers. Combining information from
locations and services is one of the key benefits of se-
mantic applications.
Current approaches usually limit their queries to
a number of particularly useful and popular services
like for instance Swoogle, geonames, or Dbpedia.
Research on automated web service discovery and
matching (Gupta et al., 2007) focuses on enhanced
applications, capable of identifying and interfacing
relevant resources in real time. Future implemen-
tations, therefore, could theoretically issue queries
spawning vast collections of different data sources,
providing even more enhanced and accurate informa-
tion. Obviously, such query strategies - if applied by
a large enough number of clients - impose a consider-
able load on the affected services, even if only small
pieces of information are requested. The World Wide
Web Consortium’s (W3C) struggle against excessive
document type definition (DTD) traffic provides a re-
cent example of the impact a large number of clients
achieves. Ted Guild pointed out
1
that the W3C re-
ceives up to 130 million requests per day from broken
clients, fetching popular DTD’s over and over again,
leading to a sustained bandwidth consumption of ap-
proximately 350 Mbps.
Service provider like Google restrict the number
of queries processed on a per IP/user base to prevent
excessive use of their Web services. From a client’s
perspective overloaded Web services lead to higher
response times and therefore higher cost in terms of
processing times and service outages.
Grass and Zilberstein suggest applying value
driven information gathering (VDIG) for considering
the cost of information in query planning (Grass and
Zilberstein, 2000). VDIG focuses on the query se-
lection problem in terms of the trade off between re-
sponse time and the value of the retrieved informa-
tion. In contrast approaches addressing only the cov-
erage problem put their emphasis solely on maximiz-
ing precision and recall.
Optimizing value under scare resources is a clas-
sical problem from economics and highly related to
decision theory. In this research we apply the search-
1
p.semanticlab.net/w3dtd
111
Weichselbraun A. (2008).
STRATEGIES FOR OPTIMIZING QUERYING THIRD PARTY RESOURCES IN SEMANTIC WEB APPLICATIONS.
In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 111-118
DOI: 10.5220/0001876901110118
Copyright
c
 SciTePress

Table 1: Response times of some popular Web services.
Service Protocol t
r
˜
t
r
t
min
r
t
max
r
σ
2
t
r
Amazon REST 0.8 0.3 0.2 663.5 150.2
Dbpedia SPARQL 0.9 0.5 0.1 301.2 42.7
Del.icio.us REST 0.6 0.4 0.1 24.3 0.5
Geo REST 1.8 0.1 0.0 1160.4 771.4
Google Web 0.3 0.2 0.1 10.3 0.2
Swoogle Web 35.8 1.6 0.2 101022.2 1762682.4
Wikipedia Web 0.4 0.2 0.1 60.9 1.3
test-stop (STS) model to applications leveraging third
party resources. The STS model considers the user’s
preferences between accuracy and processing time,
maximizing the total utility in regard to these two
measures. In contrast to the approach described in
(Grass and Zilberstein, 2000) the STS model adds
support for a testing step, designed to obtain more in-
formation about the accuracy of the obtained results,
aiding the decision algorithm in its decision whether
to acquire additional information or act based on the
current answer set. Similar to (Ipeirotis et al., 2007)
the resulting query strategy might lead to less accu-
rate results than a “brute force” approach, but nev-
ertheless optimizes the balance between accuracy and
costs. This paper’s results are within the field of AI re-
search facilitating techniques from decision theory to
address problems of agent decision making (Horvitz
et al., 1988).
The article is organized as follows. Section 2
presents known query limits and response times of
some popular Web services. Section 3 provides the
theoretical background for the search-test-stop model,
and presents its extension to discrete probability func-
tions. Afterwards the application of this method to
applications utilizing external resources is outlined in
Section 4 and an evaluation of this technique is pre-
sented in Section 5. This paper closes with an outlook
and conclusions drawn in Section 6.
2 PERFORMANCE AND
SCALABILITY
As more and more applications facilitating external
data repositories emerge, strategies for a responsible
use of these resources gain in importance.
Extensive queries to external resources increases
their share of the program’s execution time and may
lead to longer response times, requiring its operators
to impose limits on the service’s use.
Even commercial providers like Google or Ama-
zon restrict the number of accesses to their services.
For instance, Google’s Web API only allows 1000 re-
quests a day, with exceptions for research projects.
Workarounds like the use of Google’s public Web in-
terface may lead to blacklisting of the client’s IP ad-
dress
2
. Google’s geo coding service imposes a limit
of 15,000 queries per day and IP address. Amazon
limits clients to 20 queries per second, but restric-
tions vary between the offered services and might
change over time
3
. Other popular resources like geon-
ames.org and Swoogle to our knowledge currently do
not impose such limits.
A Web service timing application issuing five dif-
ferent queries to popular Web resources in 30 min
intervals over a time period of five weeks yielded
Table 1 listing the services’ average response time
(t
r
), the response time’s median (
˜
t
r
), its minimum
and maximum values (t
min
r
, t
max
r
), and variance (σ
2
t
r
).
These response times vary, depending on the client’s
Internet connectivity and location, but adequate val-
ues can be easily obtained by probing the service’s
response times from the client’s location.
Table 1 suggests that Google provides a fast and
quite reliable service (σ
2
t
r
= 0.2) with only small vari-
ations in the response times. This result is not very
surprising considering the global and highly reliable
infrastructure Google employs.
Smaller information providers which cannot af-
ford this kind of infrastructure in general provide
good response times (due to fewer requests), but they
are more sensitive to sudden peaks in the number of
clients accessing their services. Table 1 reflects these
spikes in terms of higher variances and t
max
r
values.
Our experiments suggest (see Section 5) that es-
pecially clients querying services with high vari-
ances benefit from implementing the search-test-stop
model.
Another strategy from the client’s perspective is
avoiding external resources at all. Many commu-
nity projects like Wikipedia or geonames.org provide
database dumps which might be used to install a lo-
cal copy of the service. These dumps are usually
rather large (a current Wikipedia dump including all
2
p.semanticlab.net/gooso
3
developer.amazonwebservices.com
ICSOFT 2008 - International Conference on Software and Data Technologies
112

pages, discussions, and the edit history comprises ap-
proximately 6.4 GB
4
) and often outdated (Wikipedia
dumps are sometimes even more than one month old,
other services like geonames update their records very
frequently).
The import of this data requires customized tools
(like mwdumper
5
) or hacks and rarely processes with-
out major hassles. In some cases the provided files do
not contain all available data (geonames.org for in-
stance does not publish the relatedTo information)
so that querying the service cannot be avoided at all.
3 THE SEARCH-TEST-STOP
MODEL
This section outlines the basic principles of the STS
model as found in decision theory. For a detailed
description of the model please refer to MacQueen
(MacQueen, 1964) and Hartmann (Hartmann, 1985).
MacQueen (MacQueen, 1964) describes the idea
of the STS model as follows: A decision maker (a
person or an agent) searches through a population of
possible actions, sequentially discovering sets of ac-
tions (S
A
), paying a certain cost each time a new set
of actions is revealed (the search cost c
s
i
). On the first
encounter with a set of possible actions, the person
obtains some preliminary information (x
0
) about its
utility (u), based on which he can
1. continue looking for another set of possible ac-
tions (paying search cost c
s
i+1
),
2. test the retrieved set of actions, to obtain (x
1
) - a
better estimation of the actions value - paying the
test cost (c
t
i
) and based on this extended informa-
tion continue with option 1 or finish the process
with option 3, or
3. accept the current set of answers (and gain the
utility u).
The challenge is combining these three options so that
the total outcome is optimized by keeping the search
(c
s
i
) and test (c
t
i
) costs low (
∑
m
i=1
c
s
i
+
∑
n
i=1
c
t
i
) with-
out jeopardizing the obtained utility u.
Introducing the transformation r = E(u|x
0
) yields
the following description for a policy without testing:
v = vF(v)+
Z
+∞
v
r f (r)dr − c
s
(1)
with the solution v = v
0
. F(r) represent the cumula-
tive distribution function of the expected utility and
f (r ) its probability mass function. The constant c
s
4
download.wikipedia.org; 2008-03-15
5
www.mediawiki.org/wiki/MWDumper
refers to search cost and v (better v
0
) to the utility ob-
tained by the solution of this equation.
Extending Equation 1 to testing yields Equation 2:
v = vF(r
D
) + (2)
Z
r
A
r
D
T (v, r) f (r)dr +
Z
+∞
r
A
r f (r)dr − c
s
and
T (v, r
D
) = v (3)
T (v, r
A
) = r
A
(4)
T (v, r) refers to the utility gained by testing, r
D
to the
value below which the discovered action set (S
A
) will
be dropped, and r
A
to the minimal utility required for
accepting S
A
. A rational decision maker will only
resort to testing, if the utility gained outweighs its
costs and therefore the condition T(v
0
,v
0
) > v
0
holds
which is the case in the interval [r
D
,r
A
].
In the next two sections we will (i) describe the
preconditions for applying this model to a real world
use case, and (ii) present a solution for discrete data.
3.1 Preconditions
MacQueen (MacQueen, 1964) defines a number of
preconditions required for the application of the STS
model. Hartmann (Hartmann, 1985) eases some of
these restrictions yielding the following set of require-
ments for the application of the model:
1. a common probability mass function h(x
0
,x
1
,u)
exists.
2. The expected value of u given a known realization
x
0
(z = E(U|x
0
,y
0
)) exists and is finite.
3. F(z|x
0
) is stochastically increasing in x
0
. For
the concept of stochastically increasing variables
please refer to (Lehmann and Romano, 2005,
p75).
3.2 The Discrete Search-Test-Stop
Model
This research deals with discrete service response
time distributions and therefore applies the dis-
crete STS methodology. Hartmann transferred Mac-
Queen’s approach to discrete models. The following
section summarizes the most important points of his
work (Hartmann, 1985).
Hartmann starts with a triple (x
0
, x
1
, u) of discrete
probability variables, described by a common proba-
bility function h(x
0
,x
1
,u). From h Hartmann derives
1. the conditional probability function f (u|x
0
,x
1
)
and the expected value Z = E(u|x
0
,x
1
),
STRATEGIES FOR OPTIMIZING QUERYING THIRD PARTY RESOURCES IN SEMANTIC WEB APPLICATIONS
113

1. Austria/Carinthia/Spittal/Heiligenblut/Grossglockner (mountain)
2. Austria/Carinthia/Spittal/Heiligenblut (village)
3. Austria/Carinthia/Spittal (district)
4. Austria/National Park Hohe Tauern (national park)
5. Austria/Carinthia (state)
6. Austria/Salzburg (Neighbor) (state)
7. Austria/Tyrol (Neighbor) (state)
8. Austria (country)
Figure 1: Ranking of possible “correct” results for geo-tagging an article covering the “Grossglockner”.
3. the probability of x
0
, f (x
0
) and F(x
0
).
Provided that the conditions described in Sec-
tion 3.1 are fulfilled only five possible optimal poli-
cies are possible - (i) always test, (ii) never test, (iii)
test if u > u
t
, (iv) if u < u
t
, or (v) if u
t
< u < u
0
t
.
The expected utility equals to
1. E(u|x
0
) for accepting without testing,
2. T (r, v) with testing, and
3. v
0
if the action is dropped and a new set (S
A
) is
selected according to the optimal policy.
4 METHOD
This section focuses on the application of the STS
model to Web services. At first we describe heuristics
for estimating cost functions (c
s
, c
t
), and the common
probability mass function h(x
0
,x
1
,u) Afterwards the
process of applying search-test-stop to tagging appli-
cations is elaborated.
4.1 Cost functions
In the conventional STS model costs refer to the in-
vestment in terms of time and money for gathering
information. By applying this idea to software, costs
comprise all expenses in terms of CPU-time, band-
width and storage cost necessary to search for or test
certain answers.
Large scale Semantic Web projects, like the ID-
IOM media watch on climate change (Scharl et al.,
2007), process hundred thousands of pages a week.
Querying geonames for geo-tagging such numbers of
documents would add days of processing time to the
IDIOM architecture.
This research focuses solely on costs in terms of
response time, because they are the limiting factor
in our current research projects. Other applications
might require extending this approach to additional
factors like CPU-time, bandwidth, etc.
4.2 Utility Distributions
Applying the STS model to economic problems yields
cash deposits and payments. Transferring this idea
to information science is a little bit more subtle, be-
cause the utility is highly dependent on the applica-
tion and its user’s preferences. Even within one do-
main the notion of an answer set’s (S
A
) value might
not be clear. For instance in a geo context the “cor-
rect” answer for a certain problem may be a particu-
lar mountain in Austria, but the geo-tagger might not
identify the mountain but the surrounding region or
at least the state in which it is located (compare Fig-
ure 1). Assigning concrete utility values to these al-
ternatives is not possible without detailed information
regarding the application and user preferences. Ap-
proaches for evaluating the set’s value might there-
fore vary from binary methods (full score for correct
answers; no points for incomplete/incorrect answers)
to complex ontology based approaches, evaluating the
grade of correctness and severe of deviations.
4.3 Application
This work has been motivated by performance issues
in a geo-tagging application facilitating resources
from geonames.org and WordNet for improving tag-
ging accuracy. Based on the experience garnered dur-
ing the evaluation of STS models, this section will
present a heuristic for determining the cost functions
(c
s
, c
t
) and the common probability mass function
h(x
0
,x
1
,u).
4.3.1 Cost functions
Searching leads to external queries and therefore
costs. Measuring a service’s performance over a cer-
tain time period allows estimating the average re-
sponse time and variance.
STS fits best for situations, where the query cost
c
s
is in the same order as the average utility retrieved
(O(c
s
) = O(u)). In settings with O(c
s
)  O(u) the
search costs have no significant impact on the utility
Figure 1: Ranking of possible “correct” results for geo-tagging an article covering the “Grossglockner”.
2. the probability function of r, f (r|x
0
) and F(r|x
0
),
3. the probability of x
0
, f (x
0
) and F(x
0
).
Provided that the conditions described in Sec-
tion 3.1 are fulfilled only five possible optimal poli-
cies are possible - (i) always test, (ii) never test, (iii)
test if u > u
t
, (iv) if u < u
t
, or (v) if u
t
< u < u
0
t
.
The expected utility equals to
1. E(u|x
0
) for accepting without testing,
2. T (r,v) with testing, and
3. v
0
if the action is dropped and a new set (S
A
) is
selected according to the optimal policy.
4 METHOD
This section focuses on the application of the STS
model to Web services. At first we describe heuristics
for estimating cost functions (c
s
, c
t
), and the common
probability mass function h(x
0
,x
1
,u) Afterwards the
process of applying search-test-stop to tagging appli-
cations is elaborated.
4.1 Cost Functions
In the conventional STS model costs refer to the in-
vestment in terms of time and money for gathering
information. By applying this idea to software, costs
comprise all expenses in terms of CPU-time, band-
width and storage cost necessary to search for or test
certain answers.
Large scale Semantic Web projects, like the ID-
IOM media watch on climate change (Scharl et al.,
2007), process hundred thousands of pages a week.
Querying geonames for geo-tagging such numbers of
documents would add days of processing time to the
IDIOM architecture.
This research focuses solely on costs in terms of
response time, because they are the limiting factor
in our current research projects. Other applications
might require extending this approach to additional
factors like CPU-time, bandwidth, etc.
4.2 Utility Distributions
Applying the STS model to economic problems yields
cash deposits and payments. Transferring this idea
to information science is a little bit more subtle, be-
cause the utility is highly dependent on the applica-
tion and its user’s preferences. Even within one do-
main the notion of an answer set’s (S
A
) value might
not be clear. For instance in a geo context the “cor-
rect” answer for a certain problem may be a particu-
lar mountain in Austria, but the geo-tagger might not
identify the mountain but the surrounding region or
at least the state in which it is located (compare Fig-
ure 1). Assigning concrete utility values to these al-
ternatives is not possible without detailed information
regarding the application and user preferences. Ap-
proaches for evaluating the set’s value might there-
fore vary from binary methods (full score for correct
answers; no points for incomplete/incorrect answers)
to complex ontology based approaches, evaluating the
grade of correctness and severe of deviations.
4.3 Application
This work has been motivated by performance issues
in a geo-tagging application facilitating resources
from geonames.org and WordNet for improving tag-
ging accuracy. Based on the experience garnered dur-
ing the evaluation of STS models, this section will
present a heuristic for determining the cost functions
(c
s
, c
t
) and the common probability mass function
h(x
0
,x
1
,u).
4.3.1 Cost Functions
Searching leads to external queries and therefore
costs. Measuring a service’s performance over a cer-
tain time period allows estimating the average re-
sponse time and variance.
STS fits best for situations, where the query cost
c
s
is in the same order as the average utility retrieved
(O(c
s
) = O(u)). In settings with O(c
s
)  O(u) the
search costs have no significant impact on the utility
and if O(c
s
)  O(u) no searching will take place at
ICSOFT 2008 - International Conference on Software and Data Technologies
114

Figure 2: Database schema of a simple tagger.
all (because the involved costs are much higher than
the possible benefit).
In real world situations the translation from search
times to costs is highly user dependent. To simplify
the comparison of the results, this research applies a
linear translation function c
s
= λ ·t
s
with λ = const =
1/
˜
t
s
yielding costs of O(c
s
) = 1. To reduce the in-
fluence of service outages the median of the response
times
˜
t
s
has been selected and a timeout of 60 seconds
for any search operation is implemented.
4.3.2 Utility Distribution
The discrete common probability mass function h is
composed of three components: The probability mass
function of (i) the utility u, (ii) the random variable
x
0
providing an estimate of the utility and, (iii) the
random variable x
1
containing a refined estimate of
the answer’s utility.
In general a utility function assuming linearly in-
dependent utility values might look like Equation 5.
u =
∑
S
A
λ(i) f
eval
(i) (5)
The utility equals to the sum of the utility gained by
each answer set S
A
, which is evaluated using an eval-
uation function f
eval
, and weighted with a factor λ(i).
To simplify the computation of the utility we consider
only correct answers as useful (Equation 6) and apply
the same weight (λ(i) = const = 1) to all answers.
f
eval
(i) =
(
0 if a
i
incorrect;
1 if a
i
correct.
(6)
Geo-tagging identifies geographic entities based on a
knowledge base as for instance a gazetteer or a trained
artificial intelligence algorithm.
After searching the number of identified entries
(|S
a
| = x
0
) provides a good estimation of the expected
value of the answers utility. Applying a focus algo-
rithm (e.g. (Amitay et al., 2004)) yields a refined
evaluation of the entity set (|S
0
a
| = x
1
) resolving geo
ambiguities. S
0
a
might still contain incorrect answers
due to errors in the geo disambiguation or due to am-
biguous terms not resolved by the focus algorithm
(e.g. turkey/bird versus Turkey/country). Based on
the probabilities of a particular answer a
i
∈ S
a
/a
0
i
∈ S
0
a
of being incorrect P
incorr
(a
i
)/P
incorr
(a
0
i
) the expected
value u for a given combination of x
0
, x
1
is deter-
mined. Evaluating historical error rates yields esti-
mations for P
incorr
(a
i
) and P
incorr
(a
0
i
).
If no historical data is available heuristics based
on the number of ambiguous geo-entries are useful
for providing an educated guess of the probabilities.
A tagger recognizes patterns based on a pat-
tern database table. The relation hasPattern trans-
lates these patterns to TaggingEntities as for instance
spatial locations, persons, and organizations. Fig-
ure 2 visualizes a possible database layout for such
a tagger. Unfortunately, the hasPattern table of-
ten does not provide a unique mapping between pat-
terns and entities - names as for instance Vienna
may refer to multiple entities (Vienna/Austria ver-
sus Vienna/Virgina/US). On the other side many enti-
ties have multiple patterns associated with them (e.g.
Wien, Vienna, Vienne, Bech, etc.). Based on the
database schema above, P
incorr
(a
i
) for such a tagger
is estimated using the following heuristic:
n
Entities
= |TaggingEntity| (7)
n
Mappings
= |hasPattern| (8)
n
ambiguous
= |σ
[isAmbiguous=
0
true
0
]
( (9)
TaggingEntry ∗ hasPattern)|
P
incorr
= 1 −
n
Entries
n
Mappings
+ n
ambiguous
(10)
Extending the database schema visualized in Fig-
ure 2 to non geo entries using WordNet and applying
Equations 7-10 yields P
incorr
(a
0
i
).
5 EVALUATION
For evaluating the STS model’s efficiency in real
world applications a simulation framework, support-
ing (i) item a solely coverage based decision logic
and the search-test-stop model, (ii) artificial (normal
distribution) and measured (compare Section 2) dis-
tributions of network response times, and (iii) com-
mon probability mass functions h(x
0
,x
1
,u) composed
STRATEGIES FOR OPTIMIZING QUERYING THIRD PARTY RESOURCES IN SEMANTIC WEB APPLICATIONS
115

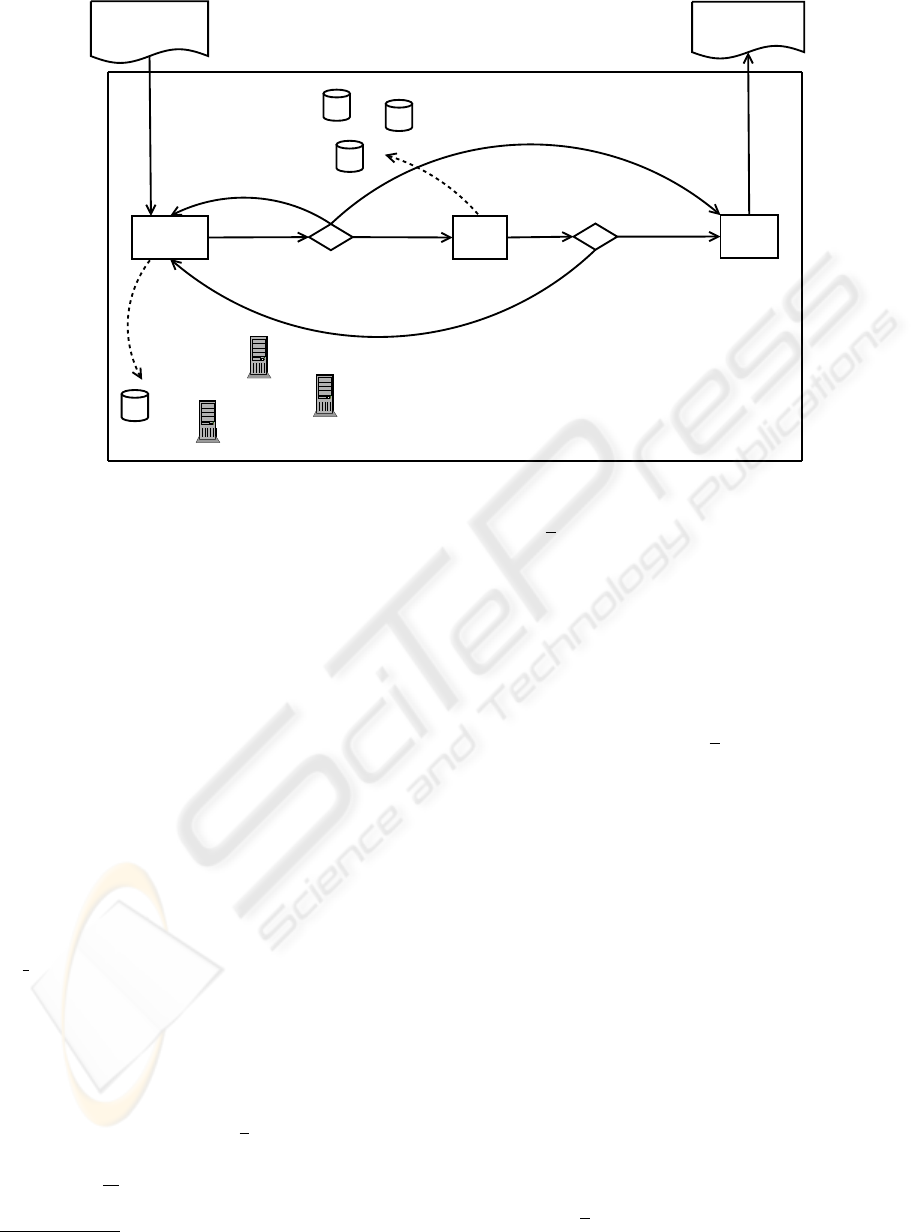
Search Test
Stop
Folksonomies
Ontology Search
Engine
SPARQL-Endpoints
DB
Business Logic
searching:
get answers
{a_1, ... a_n}
and probabilities
X_0; pay c_s
Ontologies
RDF Data
testing answers:
get refined probabilities X_1;
pay c_t
stop and get
the utility minus
the costs
accumulated.
c
c
Input Query
Response
Figure 3: The search-test-stop approach.
from user defined P
incorr
(a
i
) and P
incorr
(a
0
i
) settings
has been programmed.
Integration of the python numarray library
6
en-
ables efficient processing of matrix operations as re-
quired for computing decisions based on the search-
test-stop model.
To prevent the coverage based decision logic from
delivering large amounts of low quality answers,
the simulation controller only accepts answers with
an expected utility above a certain threshold (u
min
).
In contrast the search-test-stop algorithm computes
u
min
= r
D
on the fly, based on the current responsive-
ness of the external service and the user’s preferences.
5.1 Performance
Comparing the two approaches at different mini-
mum quality levels (u
min
), and service response time
distributions approximated by a normal distribution
N(t, σ
2
t
) yields Table 2. The common probability
mass functions has been composed with P
incorr
(a
i
) =
0.3, P
incorr
(a
0
i
) = 0.1. The parameters for the nor-
mal distribution are c
s
= N(2,1.9) for high search
costs, c
s
= N(1,0.9) for medium search costs, and
c
s
= N(0.5,0.4) for low search costs.
Table 2 evaluates the search strategies according
to two criteria: (i) the quality u, the average utility of
an answer set (S
A
) retrieved by the strategy, and (ii)
the quantity
∆u
∆t
- the rate at which the number of cor-
rect answers (and therefore the total utility (u)) grows.
6
sourceforge.net/projects/numpy
High u values correspond to accepting only high
quality results, with a lot of correct answers, and drop-
ping low quality answer sets (at the cost of a lower
quantity).
The conventional coverage based approach
(Conv) delivers the highest quantity for small u
min
values because virtually all answers are accepted and
contribute to the total utility. This greedy approach
comes at the cost of a lower answer quality and
therefore low average utility u per answer. Increas-
ing u
min
yields a better answer quality, but lower
quantity values. At high search costs this strategy’s
performance is particularly unsatisfactory, because it
doesn’t consider the costs of the search operation.
In contrast to the conventional approach STS max-
imizes answer quality and quantity based on the cur-
rent search cost adjusting queries to the responsive-
ness of the service and the user’s preferences. These
preferences formalize the trade off between quality
and quantity by specifying a transformation function
between search cost and search times.
STS therefore optimizes the agent’s behavior in
terms of user utility. This does not mean that STS
minimizes resource usage. Instead STS dynamically
adjusts the resource utilization based on the cost of
searching (c
s
) and testing (c
t
), providing the user with
optimal results in terms of accuracy and response
times.
Enforcing a minimal utility u
min
boosts the av-
erage utility u of the non STS service, but at the
cost of a higher resource utilization, independent from
ICSOFT 2008 - International Conference on Software and Data Technologies
116

-4000
-2000
0
2000
4000
6000
8000
10000
12000
14000
0 20000 40000 60000 80000 100000 120000
swoogle.umbc.edu; u_min=4.00
Sts - time efficiency
Non_sts - time efficiency
(a) Swoogle;
˜
t=1.6
0
2000
4000
6000
8000
10000
12000
14000
0 1000 2000 3000 4000 5000 6000 7000 8000
google.com; u_min=4.00
Sts - time efficiency
Non_sts - time efficiency
(b) Google;
˜
t=0.2
-10000
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
10000
0 20000 40000 60000 80000 100000
geonames.org; u_min=4.00
Sts - time efficiency
Non_sts - time efficiency
(c) geonames.org;
˜
t=0.1
0
200
400
600
800
1000
1200
0 1000 2000 3000 4000 5000
geonames.org
(d) Search times at geonames.org
Figure 4: Search-test-stop (STS) versus conventional (NON-STS) decision logic.
Table 2: Tagging performance.
Search Quality (u) Quantity (
∆u
∆t
)
Cost (c
s
) u
min
STS Conv STS Conv
low 2 6.62 5.58 3.47 7.79
low 4 6.64 6.13 3.56 6.93
low 6 6.69 6.55 3.57 5.95
low 8 6.66 6.39 3.55 2.75
medium 2 4.99 4.84 1.88 3.22
medium 4 5.02 5.15 1.92 2.76
medium 6 5.01 5.32 1.89 2.27
medium 8 5.00 3.86 1.87 0.79
high 2 2.81 3.20 0.78 1.05
high 4 2.75 3.25 0.76 0.88
high 6 2.84 2.81 0.80 0.59
high 8 2.81 -0.91 0.76 -0.09
the server’s load (leading to extremely high response
times during high load conditions). Static limits also
do not consider additional queries at idle servers,
leading to lower utilities under low load conditions.
In contrast to the conventional approach STS (i) uti-
lizes dormant resources of idle servers, and (ii) spares
resources of busy servers, maximizing utility accord-
ing to the user’s preferences.
5.2 Web Services
In this section we will simulate the effect of STS
on the performance of real world Web services, us-
ing search costs as measured during the Web service
timing (compare Section 2). Figure 4 visualizes the
application of the search-test-stop model to Web ser-
vices. The simulation facilitates the cost and common
probability mass functions from Section 5.
Figure 4 compares the tagger’s performance for
three different Web services (Swoogle, Google, geo-
names) with u
min
= 4. The fourth figure visualizes
geoname’s response times over the observation period
of five weeks. In all three use cases STS performs
well, because the search times are adjusted accord-
ing to the service’s responsiveness. Geonames and
STRATEGIES FOR OPTIMIZING QUERYING THIRD PARTY RESOURCES IN SEMANTIC WEB APPLICATIONS
117

Swoogle experience the highest performance boost,
due to high variances in the search cost, leading
to negative utility for the conventional query strat-
egy. Services with low variances (σ
2
t
r
) in their re-
sponse times as for instance Google, del.icio.us and
Wikipedia benefit least from the application of the
STS model, because static strategies perform better
under these conditions.
6 OUTLOOK AND
CONCLUSIONS
This work presents an approach for optimizing ac-
cess to third party remote resources. Optimizing the
clients resource access strategy yields higher query
performance and spares remote resources by prevent-
ing unnecessary queries.
The main contributions of this paper are (i) apply-
ing the search-test-stop model to value driven infor-
mation gathering, extending its usefulness to domains
where one or more testings steps allow refining the
estimated utility of the answer set; (ii) demonstrating
the use of this approach to semantic tagging, and (iii)
evaluating how the search-test-stop model performs
in comparison to a solely value based approach.
The experiments show that search-test-stop and
value driven information gathering perform especially
well in domains with highly variable search cost.
In this work we only use one level testing, never-
theless, as Hartmann has shown (Hartmann, 1985) ex-
tending STS to n-levels of testing is a straight forward
task. Future research will transfer these techniques
and results to more complex use cases integrating
multiple data sources as for instance semi automatic
ontology extension (Liu et al., 2005). The develop-
ment of utility functions considering partially correct
answers and user preferences will allow a more fine
grained control over the process’s performance yield-
ing highly accurate querying strategies and therefore
better results.
ACKNOWLEDGEMENTS
The author wishes to thank Prof. Wolfgang Janko
for his valuable feedback and suggestions. The
project results have been developed in the IDIOM
(Information Diffusion across Interactive Online Me-
dia; www.idiom.at) project funded by the Aus-
trian Ministry of Transport, Innovation & Technol-
ogy (BMVIT) and the Austrian Research Promotion
Agency (FFG).
REFERENCES
Amitay, E., Har’El, N., Sivan, R., and Soffer, A. (2004).
Web-a-where: geotagging web content. In SIGIR ’04:
Proceedings of the 27th annual international ACM SI-
GIR conference on Research and development in in-
formation retrieval, pages 273–280, New York, NY,
USA. ACM.
Grass, J. and Zilberstein, S. (March 2000). A value-driven
system for autonomous information gathering. Jour-
nal of Intelligent Information Systems, 14:5–27(23).
Gupta, C., Bhowmik, R., Head, M. R., Govindaraju, M.,
and Meng, W. (2007). Improving performance of web
services query matchmaking with automated knowl-
edge acquisition. In Web Intelligence, pages 559–563.
IEEE Computer Society.
Hartmann, J. (1985). Wirtschaftliche Alternativensuche
mit Informationsbeschaffung unter Unsicherheit. PhD
thesis, Universit
¨
ot Fridericiana Karlsruhe.
Horvitz, E. J., Breese, J. S., and Henrion, M. (1988). De-
cision theory in expert systems and artificial intelli-
gence. International Journal of Approximate Reason-
ing, 2:247–302.
Ipeirotis, P. G., Agichtein, E., Jain, P., and Gravano, L.
(2007). Towards a query optimizer for text-centric
tasks. ACM Trans. Database Syst., 32(4):21.
Lehmann, E. L. and Romano, J. P. (2005). Testing Statistical
Hypotheses. Springer, New York, 3rd edition edition.
Liu, W., Weichselbraun, A., Scharl, A., and Chang, E.
(2005). Semi-automatic ontology extension using
spreading activation. Journal of Universal Knowledge
Management, 0(1):50–58.
MacQueen, J. (1964). Optimal policies for a class of
search and evaluation problems. Management Sci-
ence, 10(4):746–759.
Scharl, A., Weichselbraun, A., and Liu, W. (2007). Track-
ing and modelling information diffusion across inter-
active online media. International Journal of Meta-
data, Semantics and Ontologies, 2(2):136–145.
ICSOFT 2008 - International Conference on Software and Data Technologies
118