RELATIONSHIP BETWEEN FRACTAL DIMENSION

AND SENSITIVITY INDEX OF PRODUCT PACKAGING

Mayumi Oyama-Higa

and Tiejun Miao

Department of Integrated Psychological Science, Kwansei Gakuin University

1-1-155, Ichibancho, Uegahara, Nishinomiya-City, 662-8501, Japan

CCI Corporation, Kitashinagawa, Shinagawa, Tokyo 141-0001, Japan

Keywords: Fractal dimension, Sensitivity index, Product packaging.

Abstract: Until now, the evaluation of product packaging has been performed subjectively since no other way existed.

Previous research has also shown that people tend to prefer images with high fractal dimension. If so, then

the fractal dimension of product package images should enable a determination of how preferable product

packages would be, or function as an index to estimate whether product packages would attract attention. In

this study, we calculated the fractal dimension for packages of 45 types of canned beer. We performed a

comparative analysis using the standard deviation method to determine the degree to which the product

packages influenced the potential customer’s impression of the product. The results showed that the fractal

dimension is highly important to an objective evaluation.

1 INTRODUCTION

Product packaging is an extremely important factor

that affects the sales of a product. Product packaging

serves several roles including protecting and

wrapping the product, facilitating transport and

storage, conveying product information to the

consumer, giving an impression about the product,

and motivating consumers to want to buy the

product. Furthermore, product package design is a

factor that even determines the image of the product

contained in the package.

Until now, package evaluations were performed

subjectively and obtaining objective evaluations

based on numerical values was not possible.

However, if people tend to prefer images with a high

fractal dimension, then an examination of the fractal

dimension of product package images could help

determine how preferable a product package would

be, or serve as one index for evaluating whether a

product package would attract attention.

Previous research related to product packages

have focused on aspects related to the buyer’s

motives in purchasing food or daily use items

(Nagamachi, 1995). We investigated whether

university students considered color, package

design, product design, quality, advertising, style,

brand, manufacturer, price, form, safety, and

functionality in their purchase decisions, and

concluded that package design was the most

important factor. In addition, in research regarding

the affect of visual sensory information on taste,

Sakai & Morikawa (2006) showed that evaluation

scores differed if the visual sensory information was

changed, even when assessing the same food

product(Sakai, Morikawa, 2006).

Fractal dimension research related to the

agreeability of human faces (Oyama-Higa, Miao, &

Ito 2007) showed a tendency for photographs of

smiling faces to have a higher fractal dimension than

photographs of expressionless faces (Oyama-Higa,

Miao & Itoh, 2007). Furthermore, research

investigating the relationship between eye

movement while viewing pictures and the fractal

dimension of those pictures (Nagai, Oyama-Higa, &

Miao 2007) has shown that the gaze tends to be

concentrated on areas of pictures with high fractal

dimension.

In this study, we calculated the fractal dimension

for canned beer packaging to determine the

relationship between the package and the buyer’s

impression of the product. The experiment overview

and method are described in section 2. Section 3

describes the fractal dimension calculation and the

relationship with the standard deviation (SD)

349

Oyama-Higa M. and Miao T. (2008).

RELATIONSHIP BETWEEN FRACTAL DIMENSION AND SENSITIVITY INDEX OF PRODUCT PACKAGING.

In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 349-355

DOI: 10.5220/0001878803490355

 SciTePress

method of evaluation. The calculation results and

perspectives for the future are discussed in section 4.

2 EXPERIMENT OVERVIEW

AND EXPERIMENT METHOD

The experiment was performed in a laboratory from

September 25 through October 3, 2007. Eighteen

subjects (11 men and 7 women) ranging in age from

19 to 26 years (mean 22 years) participated. None of

the subjects had ever previously consumed the

various canned beers shown in the photographs. All

subjects had normal vision.

2.1 Fractal Dimension Calculation

and Grouping

First, the photograph of each of the 45 types of

canned beer was assigned a number from 1 to 45,

and the fractal dimension was calculated for each

photograph using the planar and cubic methods. See

the Appendix for details of calculating the fractal

dimension.

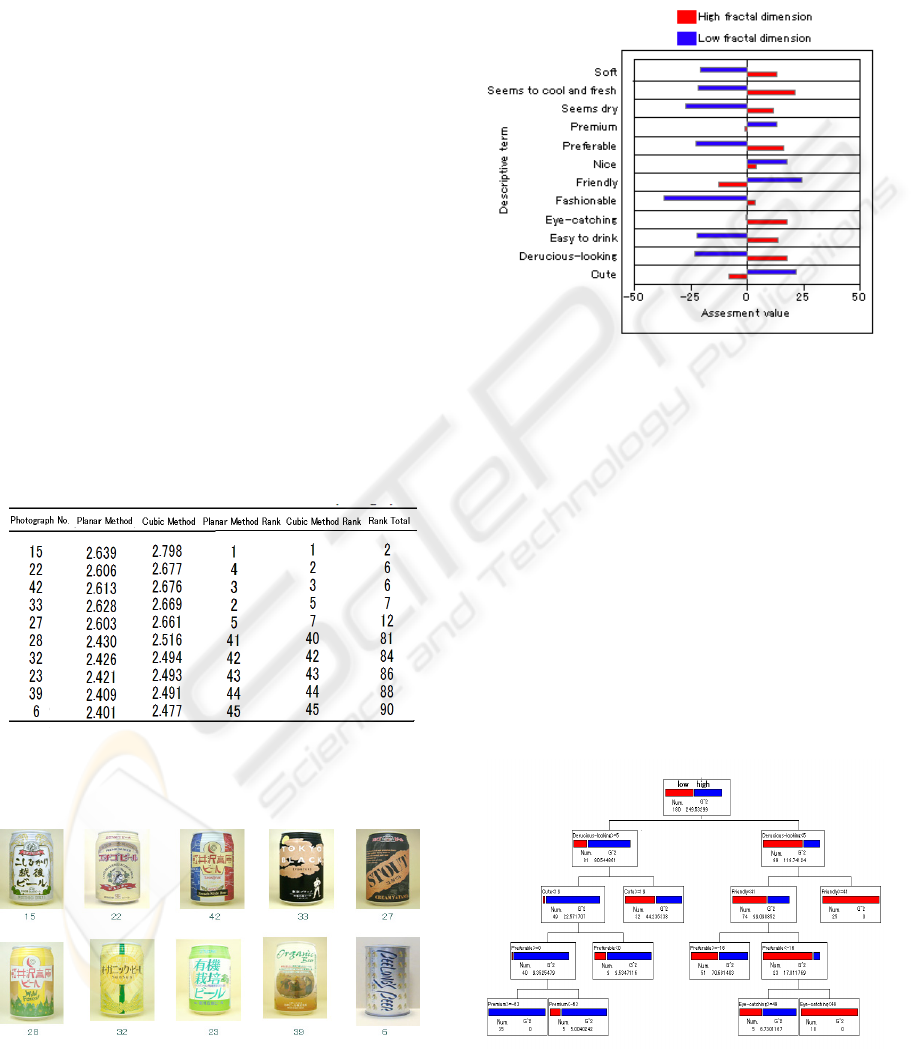
The photographs were ranked in descending order

by fractal dimension according to the results of the

planar and cubic methods. The five photographs

with the lowest total based on the two methods

(hereafter referred to as the high fractal group), and

the five photographs having the highest total

(hereafter referred to as the low fractal group) were

extracted and selected for further evaluation using

the SD method.

Figure 1: Selection of targets for the SD method of

assessment.

2.2 Assessment by the SD Method

A chair was placed so that the eye level of a subject

sitting in it would be at the same height as the center

of a computer display 57 cm away. Five photographs

from the high fractal group and five photographs

from the low fractal group were randomly displayed,

and subjects were asked to assess each photograph

one at a time on the computer display (Figure. 2).

Figure 2: Assessment screen based on the SD method.

The 16 descriptive terms used in the SD method, the

order of presentation, and positive or negative

orientation are shown in Table 1. The order of

presentation and positive or negative orientation

were determined randomly.

The 16 terms were randomly selected from a list of

sensitivity words created by Nagamachi, (1995) that

were thought to be relevant to impressions of canned

beer [2].

Table 1: Descriptive terms used in the SD method.

Adjective number Descriptive terms

1 Difficult to drink Easy to drink

2 Preferable Not preferable

3 Not refreshing Refreshing

4 Would not like to buy Would like to buy

5 Expensive-looking Not expensive-looking

6 Not friendly Friendly

7 Warm Chilling

8 Seems dry Does not seem dry

9 Seems cool and fresh Does not seem cool and fresh

10 Not soft Soft

11 Not fashionable Fashionable

12 Eye-catching Subdued

13 Not cute Cute

14 Delicious-looking Not delicious-looking

15 Not premium Premium

16 Nice Not nice

The estimation screen was 500 × 700 pixels centered

in the display. A photograph of the canned beer was

ICSOFT 2008 - International Conference on Software and Data Technologies

350

presented on the left half of the screen at a size of

239 × 358 pixels, and eight sliders paired with

opposing adjectives were presented on the right half

of the screen.

The sliders could be moved by dragging the mouse,

and subjects were instructed to move the slider to the

position they felt appropriate for that product.

Assessment values were designed to record a

maximum value of 100 and a minimum value of –

100.

3 RELATIONSHIP BETWEEN

THE FRACTAL DIMENSION

CALCULATION

AND SD METHOD

ASSESSMENT VALUES

3.1 Fractal Dimension Calculation

The fractal dimensions of the beer photographs in

the high and low fractal groups used in the SD

estimation method (Figure. 3) are shown in Table 2.

Table 2: Fractal dimension and rank of assesd canned beer

photographs.

3.2 Relationship between Fractal

Dimension and Assessment Values

Figure 3: High fractal group (upper row) and low fractal

group (lower row) of canned beer photographs and

photograph numbers.

We divided fractal dimension into two groups (high

value/low value) and performed Student t-test

(Alpha 0.05) of 16 term of SD using all subject data.

As a result, we found twelve terms that were

significantly different relations. Fig. 4 shows the

results.

Figure 4: Bar graph of descriptive terms which are

significantly different with high/low of the fractal

dimension.

We performed partition analysis of 12 items where

significant difference was seen in. Fig 5.

As a result, three remarkable rules were found.

A. The rule of the high fractal dimension.

Rule 1. 35 cases in 90 (38.9%)

Premium ≧ -63、Preferable ≧ 0,

Cute <16, and Delicious-looking ≧ 5

B. The rule of the low fractal dimension.

Rule 2. 25 cases in 90 (27.8%)

Friendly ≧ 41 and Delicious-looking ＜ 5

Rule 3. 19 cases in 90 (21.1%)

Eye-catching ＜ 49, Preferable ＜ -16,

Friendly ＜ 41 and Delicious-looking ＜ 5

Figure 5: Partition analysis of twelve items.

RELATIONSHIP BETWEEN FRACTAL DIMENSION AND SENSITIVITY INDEX OF PRODUCT PACKAGING

351

The correlation coefficients between the fractal

dimensions calculated by the planar method and the

assessment values are shown in Table 3.

Furthermore, the correlation coefficients between

the fractal dimensions calculated by the cubic

method and assessment values are given in Table 4.

Table 3: Correlation coefficient between the planar

method fractal dimension and the assessment value of

each descriptor.

Table 4: Correlation coefficient between the cubic method

fractal dimension and the assessment value of each

descriptor.

For Pearson’s correlation coefficient, when using a

non-correlated test of each adjective assessment

value and the fractal dimension of the planar

method, significant correlations were found for

“would like to buy” (t = 3.98, df = 8, p < .01),

“expensive-looking” (t = 4.23, df = 8, p < .01),

“delicious-looking” (t = 4.85, df = 8, p < .01), and

“premium” (t = 4.47, df = 8, p < .01). A similar

tendency was observed in the results of the cubic

method.

3.3 Discovering Latent Factors using

the Assessment Value Factor

Analysis

A factor analysis based on the principal factor

method was performed to reveal latent adjective

factors. Rotation was performed using the promax

rotation method, and three factors were extracted.

The factor matrix for each adjective is shown in

Table 5.

The first factor was set to “desire to purchase quality

products” because all of the following terms were

included: “would like to buy,” “delicious looking,”

“expensive looking,” “cool,” and “premium.” The

second factor was set to “soft feeling” because the

adjectives such as “soft” and “warm” were included.

The third factor was set to “light feeling” because

the adjectives “refreshing” and “dry” were included.

Table 5: Factor matrix of each descriptor.

3.4 Relationship between Fractal

Dimension and Latent Factors

The correlation coefficients between extracted

factors and fractal dimension are shown in Table 6.

Table 6: Pearson’s correlation coefficient of the fractal

dimension and each factor.

For Pearson's correlation coefficient, when

performing a non-correlated test, a significant

correlation was found between the fractal dimension

of planar method and the first factor, “desire to

purchase quality products” (t = 4.31, df = 8, p < .01).

A significant correlation was also found between the

ICSOFT 2008 - International Conference on Software and Data Technologies

352

fractal dimension of cubic method and the factor

“desire to purchase quality products” (t = 4.11, df =

8, p < .01).

Table 6 shows a high correlation between the first

factor (desire to purchase quality products) and both

the planar and cubic fractal dimensions, indicating a

negative correlation between the second factor (soft

feeling) and the fractal dimension.

3.5 Evaluation of the Result

The canned beer used to compare labels omits the

one of a famous beer company in Japan. Therefore,

this investigation was done by using the local beer

not notorious.

Result of examining hot seller of beer by the Internet

later. The 33rd canned beers with high fractal

dimension of Fig. 3 were a local beer hot selling

rankings and 1st place.

(http://www.rakuten.co.jp/yonayona/111011/718975/#

tp24)

The 42nd was popular ability No.1.

(http://store.shopping.yahoo.co.jp/yoho-

yonayona/b7dab0e6c2.html)

Moreover, popularity was high, and the 15th and

22nd canned beers had been won the championship

in the contest of the beer.

(http://www.rakuten.co.jp/yagishoten/425762/448054/)

The canned beer with low fractal dimension was not

displayed in sales information in the Internet.

The beer is drunk all over the world. The SD

evaluation that we used is thought to be different in

the culture and the climate. This testee is a young

person in Japan. 45 kinds of canned beers used to

experiment are not brands known well in Japan.

Therefore, the testee had not seen the label of

local beer. In a word, the testee who did not have the

experience of drinking each beer was chosen.

It can be thought that the fractal dimension is related

to the buying intention from the above-mentioned

result.

4 DISCUSSION

Biological information exhibits a chaotic behavior,

and until now, it has been difficult to explain human

information processing using subjective methods

(Miao, Shimoyama, Shimizu, Oyama-Higa,2006),

(Barnsley, M. B., 1988) . In other words, delicate

human information processing, in particular, cannot

be analyzed in detail by traditional linear analytical

methods. By using nonlinear and complexity

methods of facial fractal analysis, our findings

suggest that information processing in human

recognition might be explained and characterized by

fractal dimensions.

We demonstrated that higher fractal dimensions

of canned beer packaging led to an increased

impression of high quality and a greater desire to

purchase. Moreover, the analysis showed that low

fractal dimensions of canned beer packages

contributed to a soft feel. The analysis results

indicated a tendency for the third factor, “light feel,”

to be perceived for low fractal dimensions.

From the calculations of fractal dimensions for

canned beer package photographs and the results of

the SD method, a high correlation was found based

on Pearson's correlation coefficients for the

descriptors “would like to buy,” “delicious-looking,”

and “premium.” Since a significant difference was

detected between the high fractal group and the low

fractal group for the terms “would like to buy,”

“delicious-looking,” and “premium," canned beer

photographs with high fractal dimensions should be

perceived as being more desirable to buy, more

delicious-looking, and of higher premium quality.

Although traditionally, resorting to subjective

assessments such as the SD method used in this

experiment would have been necessary to measure

the good or bad aspects of product packaging, these

results showed the feasibility of calculating the

fractal dimension of such product packaging to

obtain an objective index of such aspects.

Further research is required to gather data on a

variety of product types and a broader range of ages

and subjects most appropriately suited to the

products being examined.

ACKNOWLEDGEMENTS

We thank Mr. Yu Toishi of the Oyama laboratories,

Kwansei Gakuin University which cooperated with

making of experimental data of packaging.

REFERENCES

Barnsley, M. B., 1988. The book, Fractals Everywhere.

Academic Press Inc., London.

Nagamachi, M., 1995. The story of sensitive engineering,

Tokyo, Japan Standards Association.

Jun, S., & Kamahori, F. 2003. Study about food and a

purchase action of life armamentarium of a university

student. Design Studies, 50(5), pp. 31–39.

Mandelbrot, B. 1977. The book, Fractals: Form, Chance

and Dimension. W. H. Freeman & Co., San Francisco.

RELATIONSHIP BETWEEN FRACTAL DIMENSION AND SENSITIVITY INDEX OF PRODUCT PACKAGING

353

Miao, T., Shimoyama, O., Shimizu, T., & Oyama-Higa,

M. 2006. Fractal analysis of facial skin thermogram

due to mental tasks. IEEE International Conference on

Systems, Man and Cybernetics, Oct. 8–11, 2006,

Taiwan, pp. 1671–1675.

Nagai, M., Oyama-Higa, M., & Miao, T. 2007.

Relationship between image gaze location and fractal

dimension. IEEE International Conference on

Systems, Man and Cybernetics, Oct. 7–10, 2007,

Montreal, pp. 4014–4018.

Oyama-Higa, M., Miao, T., & Itoh, T. 2007. Relationship

between fractal dimension and agreeability of facial

imagery. Computational Models for Life Sciences–

CMLS '07: 2007 International Symposium on

Computational Models of Life Sciences. AIP

Conference Proceedings, 952, pp. 104–113.

Pentland, A. P. 1984 Fractal-based description of sciences.

IEEE Trans. Pattern Analysis and Machine

Intelligence, PAMI-6, pp. 661–674.

Sakai, N., & Morikawa, N.,2006. A role of an eye-sight

image in alimentary taste rating. Japanese Journal of

Taste and Smell (in Japanese), 13(3), pp. 463–466.

Shimada, S et al. 2000. The evaluation method of arousal

level by local fractal analysis of fractal skin

temperance. T. IEE Japan, 120-C, pp. 1429–1432.

APPENDIX

Fractal Dimension Estimations

The word fractal, introduced by Mandelbrot was

used to describe the irregular structure of many

natural objects and phenomena (Mandelbrot, 1977).

Fractal geometry shows that nature exhibits a

fundamental character generally known as self-

similarity. This means, that however complex the

shape and/or dynamic behavior of a system, by

observing it carefully and imaginatively, one can

find features in one scale which resemble those in

other scales.

The fractal model of an imaged 3-D surface,

including that of a digital photograph image,

provides a natural description of most textured and

shaded images. A defining characteristic of a fractal

is that it has a fractal dimension. The fractal

dimension of an image gray-level intensity surface

corresponds quite closely to our intuitive notion of

roughness. To infer the fractal dimension of a 3-D

surface from the image data, one method is to

assume the gray level I(x) at pixel x changes

according to a fractal Brownian function (Pentland,

1994). After some simplification operations, the

following relationship is given for any displacement

xΔ

(pixel) within an image

[]

CxxIxxIE

=Δ⋅−Δ+

−

)()(

, (1)

where E[ ] is the mean value when keeping

（

pixel ） fixed, and H and C are constants. By

conducting logarithm operations on equation (1), we

obtain the value of H as the slope of the regression

line fit to log–log data. The fractal dimension D of

the image surface is derived from

D = 3 – H. (2)

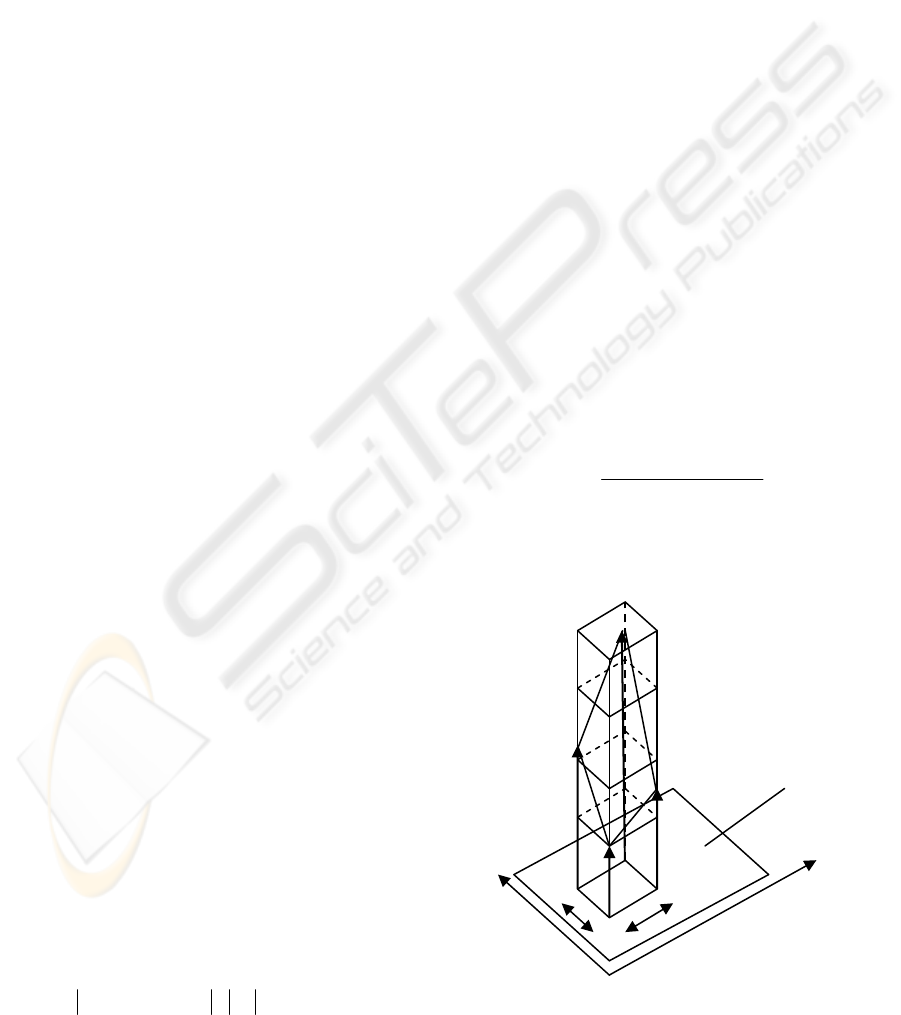
To simplify the calculation, two methods have been

developed to easily and quantitatively deal with the

imagery (Shimada et al., 2000). One of these

methods, called the cubic method, infers the fractal

dimension of the 3-D intensity surface from image

data concerning covering processes at increased

resolutions (2). Considering a cube, each edge of

which is a pixel of size r, the number of cubes

required to cover the surface of an image is N(r).

Furthermore, if the relationship

exists with a constant C, then H gives an estimation

of the fractal dimension of the image surface.

()

Nr r C

⋅

(3)

Fig 5 shows an area A on which an image surface

is assumed. Considering the volume unit of a cube

of size

rrr

and an area unit of

on A, if

the surface portion above the area of

completely covered by the cubes, the required

number n(r) is

max( ) min( )

() { } 1

n r floor

−

. (4)

In equation (4), the “floor” is the integer, and fi (I =

1, 2, 3, 4) are respective gray levels of the image

intensity.

Figure 5: Estimation of the fractal dimension over image

area A.

Area A

ICSOFT 2008 - International Conference on Software and Data Technologies

354

() () (area of )/Nr nr A r=< > ⋅

(5)

When the average value of n(r) over all of A is

denoted as <n(r)>, the total number required to

cover the image surface above A.

Finally, fractal dimension D is estimated by the

regression fit to successive log–log data points of

log10(r) vs. log10N(r), with increased sizes of r.

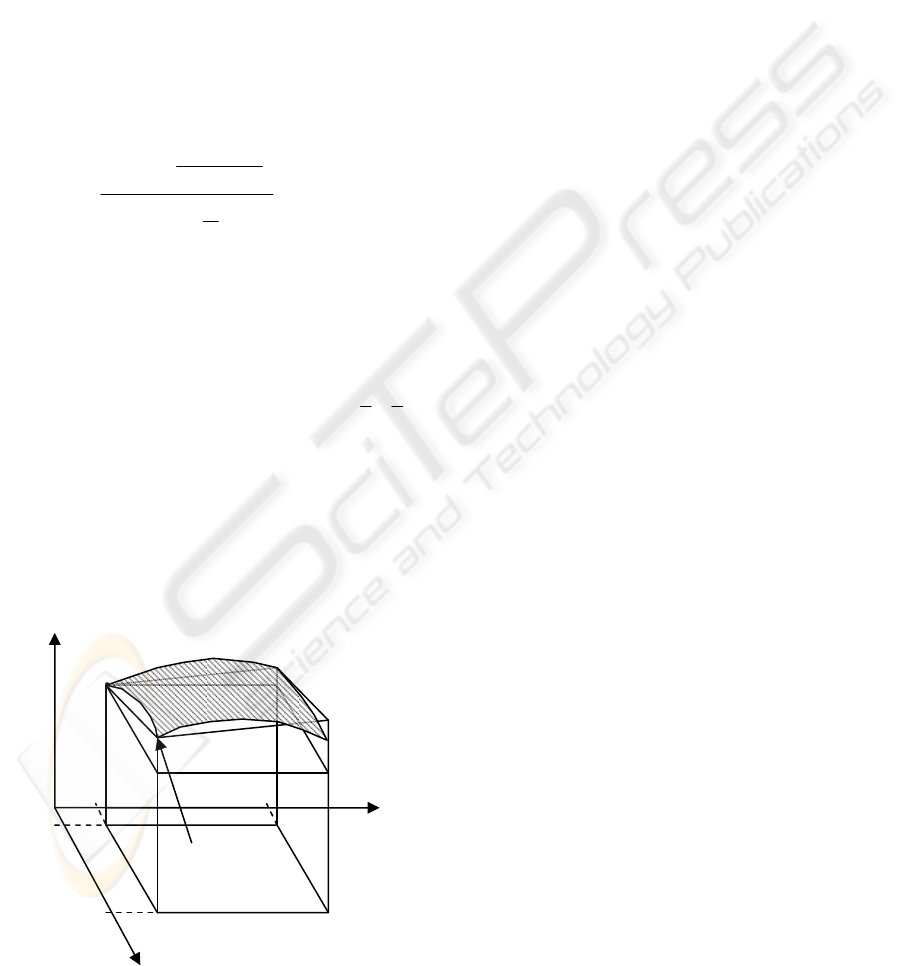
Another approach, called the area method,

involves counting the number of area units covering

an area, instead of the cubic units. This method

calculates the fractal dimension representing the

undulating complexity of the picture density by

using a method to change the degree of coarse

graining and a parameter-based model method:

[

]

[]

)

(log

)

)(

(log

tFE

atFE

−

(6)

In equation (6), setting t to a fixed value and

calculating the number of partitions by calculating

the length unit of

[]

)(aFE

as 1/a, or calculating

the number of surface partitions of the image density

curved surface as the minimum area unit of

the above equation can be represented as

(

)

aN /1

By setting

ra =/1

, equation (1) can be rewritten

)1(loglog)(log

101010

NrHrN +−=

(7)

Figure 6: Area approach to computing fractal dimensions.

For images, the calculated value on the left side of

equation (2) is dependent on r; thus, variability is

normal. However, if the image is fractal in nature,

linearity should be largely preserved.

In this way, fractal dimension

can be calculated

by determining the slope of the regression line by

the least-squares method for multiple sample values

))(log,(log

1010

rNr

),2,1( "=r

; the obtained

value can be used as an estimate for －

For two-dimensional objects such as images,

setting the image density curved surface area,

calculated using units with small areas such as

, to

)(rS

, we obtain

)()(

rNrrS ⋅=

(8)

Therefore, equation (7) can be rewritten as

)1(loglog)2()(log

101010

SrHrS +

−

(9)

Here, the surface area of an

small area density

curve is a triangular area with twice the surface area

shown in Figure 3 of

)),(,,()),,(,,()),,(,,( rjifrjijrifjrijifji

By deriving the regression line slope by the least-

squares method from multiple sample values of

))(log,(log

1010

rSr

),2,1( "=r

, the estimated

value

−

can be used to calculate the fractal

dimension

j+r

f(I,J)

(i,j, f(i,j)) (i,j+r, f(i,j+r))

( i+r,j, f(i+r,j))

RELATIONSHIP BETWEEN FRACTAL DIMENSION AND SENSITIVITY INDEX OF PRODUCT PACKAGING

355