MINING ASSOCIATION

Correlations Among Demographic Health Indicators

Subhagata Chattopadhyay, Pradeep Ray and Lesley Land

APuHC, SISTM, Australian School of Business, University of New South Wales, Sydney, NSW 2052, Australia

Keywords: Health data, Data mining, ANOVA, Regressions, QAR.

Abstract: Demographic health indicators such as crude birth rate, crude death rate, maternal mortality rate, infant

mortality rate (IMR), Adult literacy rate and many others are usually considered measures of a country’s

health status. These health indicators are often seen in an isolated manner rather than as a group of

associated events. Conventional statistical techniques often fail to mine inter-relations among these

indicators. This paper focuses on mining association-correlations among various demographic health

indicators under child immunization program, skilled obstetric practice, and IMR using both statistical and

Quantitative Association Rule (QAR) mining techniques. Relevant archived data from 10 countries located

in the Asia-Pacific region are used for this study. Finally the paper concludes that association mining with

QAR is more informative than that of statistical techniques. The reason may lie in its capability to generate

the association rules using a 2-D grid-based flexible approach. Finally it is concluded that such an approach

could be pioneering for engineering the hidden knowledge among various other health indicators.

1 INTRODUCTION

Healthcare statistics of any country is one of the

most important reflectors to assess its state of socio-

economic growth. Better socio-economic growth in

the Western world is reflected through its better

healthcare status than the developing world. Various

indicators are used for healthcare assessment. Some

of these are crude birth rate, crude death rate,

maternal mortality rate, infant mortality rate (IMR),

adult literacy rate and so forth. These indicators are

available in various URLs in the WWW

(http://www.who.int/whosis/database/core/core_sele

ct.cfm) and therefore readily available. However, on

their own, the archived demographic data may

render a picture of a country’s healthcare status but

fails to provide much insight into possible

relationships between them. Given this scenario this

paper focuses on mining underlying relationships

between IMR and other indicators related to

maternal and child health. In this paper we argue

that the outcome of these indicators is more telling

than its usual tabular or graphical representations of

data values.

Analysis of a country’s healthcare practice remains a

potential field of research for population and social

scientists since last couple of decades. Various

health indicators are studied over a period of time.

El-Ghannam (2003) has shown that the highest mean

rate of child malnutrition was found in South Asia

region (57%), while the smallest mean rate was

found in Europe region (just 1%). In West Africa

region, the average of child mortality rate per 1000,

172 children, was the highest among all regions in

the world, while in Europe was found to be 14

children per 1000. The results of their studies reveal

positive associations between illiteracy rate,

unemployment, poverty, fertility rate, family size,

food consumption, maternal mortality rate,

population per physician. D’souza and Bryant

(1999), has also corroborated the above findings of

El-Ghannam (2003). D’souza and Bryant (1999)

found a positive correlation between huge

population that leads to insufficient food and

healthcare with IMR. In another study, Byass and

BilaBavi (2003) show that ‘2-child’ policy in

Vietnam has reduced the IMR quite considerably

because of lower rate of childbirth. Crude birth rate

poses to be another useful indicator of IMR (Hynes

et al, 2002 and Bhatia et al, 2002). Adult literacy

rate (also described by El-Ghannam, 2003) remains

another useful predictor of IMR. Hossain et al.

(2007) has observed that increased literacy rate

declines IMR. Studies performed by Hales et al.

(1999) and Wu and Chiang, 2001 show that GNP

per capita, gross domestic product, national health

expenditure, public social expenditure, and Gini

coefficient may influence the occurrence of IMR.

Authors of both the studies found that income-

315

Chattopadhyay S., Ray P. and Land L. (2008).

MINING ASSOCIATION - Correlations Among Demographic Health Indicators.

In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 315-320

DOI: 10.5220/0001880203150320

 SciTePress

inequality remains the key barrier to improve IMR

and U5MR (Under 5 Mortality Rate). However, the

available literature has a couple of gaps – 1. The

analysis is made by conventional statistical

techniques that may sometimes be rigid to explain

the association-correlations among these indicators

and 2. No study has been undertaken to show

association-correlations among child immunization,

safe childbirth with that of IMR.

According to UNICEF, IMR is defined as death

of infants in a country per 1000 live births

(http://www.unicef.org/infobycountry/stats_popup1.

htm1.) and is an important health indicator (King

and Zeng, 2001). However, IMR calculation varies

across countries. The variation may lie on how a

country defines ‘life birth’ and whether all deaths

(related to child birth) are included with in the

definition of IMR. To resolve the first issue, the

World Health Organization (WHO) defines a ‘live

birth’ as any baby born with clear demonstrations of

unassisted (and independent) signs of life, such as

breathing, voluntary movement, and/or auscultable

heartbeat (WHO, 1993). In order to minimize this

problem further, UNICEF (United Nations

Children’s Fund) uses a statistical methodology to

account for these reporting differences

(http://www.unicef.org/publications/index_18108.ht

ml). In USA every case of infant mortality is

reported while many other countries do not

(MacDorman et al., 2007). On the other hand, some

countries, e.g. Vietnam don't reliably register babies

who die within the first 24 hours of birth probably

due to cultural reasons (Huy et al., 2007). Thus,

despite of the super specialized neonatal care, USA

usually comes out with a higher IMR that is a

seemingly paradoxical finding. Therefore, the

second issue is still prevailing and invites research.

Assuming that better healthcare practice may

influence the IMR this paper aims to mine

associations among various other health indicators

and attempts to link it with IMR status. It studies

how different child immunization programs (OPV,

M, DPT and BCG) and assisted deliveries (ADR)

may be associated with each other and may be

linked with ‘IMR’. Archived data of ten

neighbouring Asian countries, such as Bangladesh,

Bhutan, India, Nepal, Thailand, Myanmar,

Indonesia, Maldives, Korea and Sri Lanka are

considered for the experiment. The possible

associations among these attributes are mined and in

turn correlated using statistical and Quantitative

Association Rule (QAR) mining techniques to note

which the better method of such kind of analysis is.

The layout of the paper is as follows. Section 2

illustrates the detailed methodology of the study.

Results are displayed and discussed in Section 3.

Conclusions are drawn and future extensions of the

study are discussed in Section 4.

2 METHODOLOGY

The objective of the study is to mine the association

among a set of quantitative attributes (QA), such as

OPV, M, DPT, BCG, and ADR and link them to that

of a categorical attribute (CA) i.e., IMR. Archived

health data of ten Asian countries and are displayed

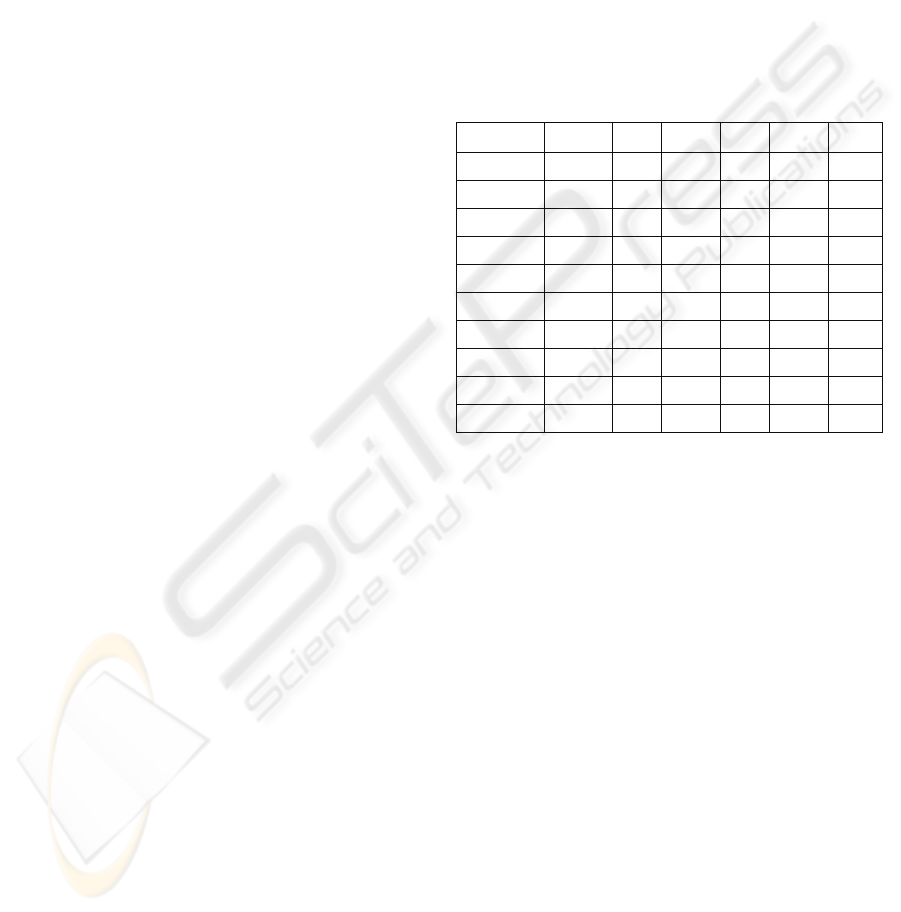
in Table 1.

Table 1: Country-wise Display of Attributes (%).

OPV M DPT BCG ADR IMR

Bangladesh

85 77 85 95 21.8 5.1

Bhutan

96 88 95 93 23.7 6.05

Nepal

76 77 75 79 13 5.9

India

70 67 70 81 42.3 6.8

Sri Lanka

98 99 78 91 97 6.42

Korea

97 95 66 88 98 2.11

Thailand

97 94 96 99 94.5 2.15

Myanmar

76 75 77 79 77.5 5.98

Indonesia

70 72 70 82 68.4 3.5

Maldives

98 97 98 98 84 1.4

2.1 Statistical Data Mining

Statistical mining of the health data is performed in

MS EXCEL2003. It is done in three steps, Step-1:

Understanding the nature of data (central tendency

and levels of data dispersions) using descriptive

statistics, Step-2: Predicting of the similarity-

dissimilarities among the QA groups using one-way

ANOVA, and Step-3: Modelling the QA-CA

relationships using simple least square regressions

2.1.1 Descriptive Statistics

As the very first step of data mining, descriptive

statistics (Rastogi, 2006) have been chosen to

summarize the central tendency and data distribution

to get an idea about the nature of data. Results

obtained are discussed in section 4.

2.1.2 One-way ANOVA

It is a measure of difference between groups on

some variable. The steps of performing ANOVA is

discussed as follows,

ICSOFT 2008 - International Conference on Software and Data Technologies

316

Step-1: Stating null hypothesis that defines that

the groups under study are indifferent, measured

from the observed F scores that are calculated as

follows,

MSEMSTRF /=

(1)

Where, MSTR and MSE indicate Mean Square

due to Treatments and Mean Square Error,

respectively, and

Step-2: Choosing a critical value (p-value) for

the test. We have chosen 0.05 for this study.

We used MS EXCEL-2003 for performing the

ANOVA test.

2.1.3 Simple Regressions

Simple regression is done for modelling the

relationships between each QA and the CA based on

the data of ten countries. Our aim is to mine the

relationships between each of the individual

quantitative attribute with that of the categorical

attribute using the following equation,

iiij

= (2)

Where, y = dependent variable (here IMR; j=1),

= intercept term,

= slope-coefficient of each

independent attribute (i=5) and

= error term,

which is the portion of the dependent variable that is

random, unexplained by any independent variable

itself. In regressions, we measure the model quality

looking at the distribution of the residuals and model

fitness by calculating the R-sq (correlation

coefficient values) and adjusted R-sq values

(Rastogi, 2006).

2.2 Association-correlation Mining

with QAR

QAR is a multidimensional Association Rule (AR)

mining technique, where the numeric attributes,

while mining are dynamically discretized for

satisfying some mining criteria, e.g. maximizing the

confidence of the mined rules (Han and Camber,

2006). As already mentioned, the objective of this

study is to mine AR using pair-wise quantitative

attributes for ten countries (i.e. observations). The 2-

D QAR grid thus generated can be generically

represented as follows,

min max min max

111

min max

( ," ... ") ( ," ... ")

(," ... ")

iii i i i

XX X X X X X X

IMR X IMR IMR

+++

∧⇒

(3)

Where, X denotes the quantitative attribute and ‘i =

5’ (OPV, M, DPT, BCG, ADR). The steps of QAR

is as follows,

1. Binning:

2. Finding frequent predicate sets

3. AR generation, and

4. Correlation analysis using ‘lift’

These are described as follows.

2.2.1 Binning

Binning is the first and most important step for the

generation of 2-D grids (taking a pair of attributes

into account). Before fitting into the grid, the

attributes (in pair) are partitioned based on equal

range (called as equal-width binning). Two-D arrays

for each possible bin combinations involving pair of

QA are thus created. Each array cell holds the

corresponding count distribution for each possible

class of the categorical attribute based on the QA.

2.2.2 Finding Frequent Predicates

In this step we aim to find frequent predicate sets

those satisfy minimum support (s) and minimum

confidence (c), where support and confidence are

calculated using the following equations in

percentage,

)(

avav

BAPs

∪

(4)

, and

)/(

avav

BAPc

(5)

respectively. Where, ‘av’ denotes the ‘average’ and

A, B are attributes.

The supports and confidence thus calculated for

all possible pairs using the following algorithm

• For each frequent item-set ‘l’, generate all

non-empty subset of l

• For every non-empty subset ‘s’ of ‘l’,

output the rule “s

⇒ (l-s)”, if csl >=)/(

Here, ‘c’ is the minimum confidence threshold

(King and Zeng, 2001). The ‘l’ denotes the

‘support_count l’ and ‘s’ indicates the

‘support_count s’. The ‘support_count’ (OPV

>av

∪ M

>av

) is the number of countries containing both

higher than average values of OPV and M and

‘support_count’ (OPV

>av

) denotes those countries

containing only higher than average values of OPV.

2.2.3 Association Rule Generation

The rules (AR) that satisfy minimum support and

minimum confidence may be denoted as ‘strong’

rules and all the strong rules are in turn, clustered.

AR, thus derived from this study is discussed in the

following section as well.

MINING ASSOCIATION - Correlations Among Demographic Health Indicators

317

2.2.4 Correlation Analysis using ‘Lift’

Lift is a correlation measure among a set of QA(s)

and is calculated as follows,

)(

)()(

)(

),(

BAc

BPAP

BAP

BAL

⇒

∪

(6)

Lift (L) is interpreted as follows,

If L>1

Positive correlation

L<1

Strong negative correlation

L = 1

Nil correlation

3 RESULTS AND DISCUSSIONS

This section displays and discusses the results

obtained from the experiments in two broad sections

1. Results of statistical data mining, and

2. Results of QAR-based data mining. Finally

these techniques are compared

3.1 Results of Statistical Data Mining

The results of statistical data mining are discussed in

the following subsections.

3.1.1 Results of Descriptive Statistics

From the values of mean, median, standard

deviations (stdev) we can state that the data are

almost normally distributed. Mean and median

values are close to each other in most of the

attributes. Skewness: it is seen that OPV, M, ADR

and IMR, i.e. >66% of the total attributes are

negatively skewed. In this study it is found that

skewness is well distributed across the attributes

ranging from –0.53 to +0.40, and 66% more towards

negative skewness. Kurtosis: Higher the kurtosis

more is the variance, which may be due to

infrequent extreme deviations, as opposed to

frequent modestly sized deviations.

3.1.2 Results of One-way ANOVA

One way or single factor ANOVA is performed on

these data set containing five quantitative attributes

(independent variables), one categorical attribute

(dependent variable) and ten observations (numbers

of countries).

The ANOVA result shows that the total sum of

squares (SS) is 14601.9 within the groups (WG)

where as the grouping accounts the SS 4522.9. The

null hypothesis was that there are no variations

among the groups of QA. Therefore, the null

hypothesis is rejected. ADR shows the highest

variation (1135). Given the small sample size

(number of observations N = 10), question may arise

whether such difference is by chance. It is explained

by the F statistic (3.48) with a p-value (0.014),

which is less than 0.05. Therefore based on these

observations we may conclude that there is indeed a

significant difference between the groups of the

quantitative parameters. In other term, as the value

of F is higher than F

crit

, (2.57) that corroborates the

difference among the QA are significant. In the

following step simple regressions are attempted to

correlate the CA with QA(s).

3.1.3 Results of Simple Regressions

Simple regressions are performed to note the

relationships between each of the QA (n=5) with

that of the CA (n=1) based on 10 observations

(N=10) keeping CI as 95%. Based on the results

found after simple regressions, it is seen that the

correlation coefficient (R-sq) values are <50% for

each case.

3.2 Results of QAR-based Data Mining

Results obtained from QAR-based mining of health

data are discussed step-wise.

3.2.1 Results of Binning

Figure 1 has shown a typical 2-D grid [OPV, M],

using equal-width distributions (61-70; 71-80; 81-

90; 91-100). Now for the country, e.g. India, OPV

(70%) and M (67%) falls on the crossed grid (0,0)

while for Korea (OPV 97%, M 95%) it is the shaded

grid and represent the corresponding categorical

attribute i.e., IMR, 6.8% and 2.11%, respectively.

Similarly for other possible pairs (maximum number

of pairs =

N −

), 2-D grids are created country-

wise and the corresponding IMR(s) could be mapped

easily. However this creates a fairly complex

scenario. The goodness of QAR is that it reduces

this complexity by accepting only those pairs where

the values are higher than the average (av) values.

For e.g., we may take only the higher values of

OPV, found in Bhutan, Sri Lanka, Korea, Thailand

and Maldives rather than taking all the values.

3.2.2 Finding Frequent Sets

At the first step, we identify the countries that

possess the QA values higher than the respective

‘av’. Using these values, then the minimum support

ICSOFT 2008 - International Conference on Software and Data Technologies

318

(s) and confidence (c) are calculated for the each

QA.

…

Figure 1: A 2-D Grid of ‘OPV-M’ Pair.

3.2.3 AR Generations

Suppose the data containing frequent predicate sets

‘l’={OPV, M, ADR} and the association rules, thus

generated as follows,

For this example, the non-empty subsets of ‘l’

according to countries are {ADR}, {OPV, M, ADR},

{OPV, M, ADR}, {OPV, M}, {OPV, M, ADR}, and

{OPV, M, ADR}. The resulting ‘c’ and ‘s’ can be

calculated as follows,

1. OPV^M

⇒ ADR, c = 5/5 = 100%; s = 5/10 =

50%; 2. OPV^ADR

⇒ M, c = 4/4 = 100%; s = 4/10

= 40%; 3. M^ADR

⇒ OPV, c = 4/5 = 80%; s =

4/10 = 40%; 4. OPV

⇒ M^ADR, c = 4/5 = 80%; s

= 4/10 = 40%; 5. M

⇒ OPV^ADR, c = 4/5 = 80%;

s = 4/10 = 40%; and 6. ADR

⇒ OPV^M, c = 4/6 =

66%; s = 4/10 = 40%.

Therefore, from the above values of ‘c’ it may be

stated that with minimum support (s) of 40%,

OPV^M

⇒ ADR is the strongest associations (c =

100%; s>40%). Similarly associations are calculated

for other combinations, e.g. DPT, M and ADR. In

this combination, the non-empty sets are {DPT,

BCG, ADR}, {DPT, BCG, ADR}, {BCG, ADR},

{DPT, BCG, ADR}, and {DPT, ADR}. The resulting

‘s’ and ‘c’ values can then be calculated as follows,

1. DPT^BCG

⇒ ADR, c = 3/5 = 60%; s = 3/10

= 30%; 2. DPT ^ADR

⇒ BCG, c = 4/4 = 100%; s =

4/10 = 40%; 3. BCG^ADR

⇒ DPT, c = 3/4 = 75%;

s = 3/10 = 30%; 4. DPT

⇒ BCG^ADR, c = 4/4 =

100%; s = 4/10 = 40%; 5. BCG

⇒ DPT^ADR, c =

4/4 = 100%; s = 4/10 = 40%; 6. ADR

⇒ DPT^BCG,

c = 3/5 = 60%; s = 3/10 = 40%.

Rule strength can be adjudged from the

minimum confidence assigned for a set of

combination. For these combinations, DPT

^ADR

⇒ BCG, DPT ⇒ BCG^ADR,

BCG

⇒ DPT^ADR have c = 100% and s>30%.

These rules are said to be strong rules because the

calculated confidence level is above the minimum

confidence and support is higher than the minimum

support. Similarly rules can be computed for

OPV^M^DPT ^BCG^ADR

⇒ IMR. It is seen that

two countries, such as Bhutan and Thailand shows

>av OPV, M, DPT, BCG and ADR values whereas

five countries show higher IMR values. From these

information we can compute the minimum‘s’ and ‘c’

values using equations 4 and 5, respectively as

OPV^M^DPT ^BCG^ADR

⇒ IMR, c = 2/5 = 40%; s

= 5/10 = 50%. We may assume that at least one

country (observation) satisfies equation 4 and 5 to

calculate the minimum confidence (c) and support

level (s) and in that case c = (1/5)*100 = 20% and s

= (1/10)*100 = 10%, may be counted as at least one

country is showing level. In our study the computed

c and s values are more than these minimum values

and predict an association among all the attributes.

From this experiment we may infer that

OPV^M

⇒ ADR has got the strongest associations

among all the possible combinations within the

OPV-M 2-D grid. On the other hand, multiple strong

associations could be mined for the

DPT^ADR

⇒ BCG,DPT ⇒ BCG^ADR and

BCG

⇒ DPT^ADR combinations. From these

association values we may predict that if a baby is

delivered under skilled supervision there is almost

100% possibility that it gets immunized with OPV

and Measles (M) vaccines and vice versa. From the

other sets of associations it may be inferred that safe

delivery under skilled obstetric supervision is

directly associated with BCG, DPT immunizations.

Therefore, we may frame a rule cluster that states if

skilled childbirth is directly associated with full

vaccinations and reflect a good maternal-and-child

health practice in any country.

3.2.4 Correlation Analysis using ‘Lift’

Using equation 6, correlations among the individual

QA are calculated. The results show that OPV, M,

DPT, BCG, ADR all are positively correlated with

each other (L<1 for all cases as s>c for all cases).

From the experimental results of OPV^M^DPT

^BCG^ADR

⇒ IMR the predicted score of L<1

suggesting strong negative correlations, i.e. if OPV,

M, DPT, BCG and ADR rates (overall immunization

rates) become high, IMR declines.

4 CONCLUSIONS AND FUTURE

WORK

The objective of this study is two-fold - firstly, to

engineer the underlying association-correlations

100

MINING ASSOCIATION - Correlations Among Demographic Health Indicators

319

among various vaccination program, safe childbirth

practice and IMR, and secondly to note which one of

the data mining techniques could be more suitable to

explain such relationships. From our experiment

based on the archived data of ten countries, we have

noticed the following,

One-way ANOVA result shows that OPV, M,

DPT, BCG and ADR are significantly dissimilar

from each other (p<0.05; F score>F

crit

) and thus can

be suitably used for predictive modeling

(regressions) as different attributes though under the

same construct (child immunization program)

Simple regressions fail to predict any significant

correlation between any of the QA (OPV, M, DPT,

BCG and ADR) and the CA, i.e. IMR as indicated

by R-sq values <50% for each analysis. But the

attempt is said to be a good one as the residual plots

are almost linear in nature without any visible

outlier.

QAR relies on 2-D grid combinations of QA and

generation of AR from confidence (c) level. From

the association rules, thus generated, it is found that

QAR is a better approach to engineer this kind of

data where direct relations cannot be statistically

predicted, but assumed. In this experiment it is

found that all the QA(s) are closely associated and

correlated with each other. From the experiment it is

found that with a combination of OPV, M and ADR

the IMR is quite low in Maldives and Thailand,

however in contrast to that Bhutan and Sri Lanka

shows a higher values. This may be due to influence

of other factors, e.g. general healthcare facilities,

literacy rate, crude birth rate and so forth. From the

other combinations DPT-BCG-ADR it is found that

rules 2,4,5 are strong rules that tells that if a baby is

born under a skilled health worker it receives DPT

and BCG vaccines and vice versa. It is true for

Thailand and Bangladesh i.e. this combination may

have reduced the IMR (but not with Bhutan).

From the ‘lift’ value, it may be observed that

there is a negative correlation between vaccination

and skilled childbirth with that of IMR, i.e. for

higher the number of immunisations and skilled

childbirth under supervisions, lower is the incidence

of IMR in a population.

However, it is important to mention here that

association mining based on a mathematical

approach may not always explain a real-world

scenario, as seen in the contrasting results of Bhutan

and Thailand. Therefore, consideration of other

health indicators could be considered in this type of

study.

REFERENCES

http://www.who.int/whosis/database/core/core_select.cfm

El-Ghannam A. R., 2003. The global problems of child

malnutrition and mortality in different world regions,

J Health Soc Policy 16(4), 1-26.

D'souza R. M., Bryant J. H., 1999. Determinants of

childhood mortality in slums of Karachi, Pakistan, J

Health Popul Dev Ctries 2(1), 33-44.

Byass P., 2003. FilaBavi Study Group, Patterns of

mortality in Bavi, Vietnam, 1999-2001, Scand J

Public Health Suppl. 62, 8-11.

Hynes M., Sheik M., Wilson H. G., Spiegel P., 2002.

Reproductive health indicators and outcomes among

refugee and internally displaced persons in post

emergency phase camps, JAMA, 288(5), 595-603.

Bhatia S., Dranyi T., Rowley D., 2002. A social and

demographic study of Tibetan refugees in India, Soc

Sci Med. 54(3), 411-22.

Hossain M. B., Phillips J. F., Pence B., 2007. The effect of

women's status on infant and child mortality in four

rural areas of Bangladesh, J Biosoc Sci. 39(3), 355-66.

Lindström C., Lindström M., 2006. Social capital," GNP

per capita, relative income, and health: an ecological

study of 23 countries, Int J Health Serv. 36(4), 679-96.

Hales S., Howden-Chapman P., Salmond C., Woodward

A., Mackenbach J., 1999. National infant mortality

rates in relation to gross national product and

distribution of income, Lancet, 354(9195), 2047.

Wu J. C., Chiang T. L., 2007. Comparing child mortality

in Taiwan and selected industrialized countries, J

Formos Med Assoc., 106(2), 177-180.

http://www.unicef.org/infobycountry/stats_popup1.htm1.

King G., Zeng L., 2001. Improving forecasts of state

failure, World Politics 53(4), 623–658.

International statistical classification of diseases and