INTERTRASM

A Depth First Search Algorithm for Mining Intertransaction Association Rules

Dan Ungureanu and Alexandru Boicea

Faculty of Automation and Computer Science, Politehnica University of Bucharest, Romania

Keywords: Intertransaction association rule mining, MFI.

Abstract: In this paper we propose an efficient method for mining frequent intertransaction itemsets. Our approach

consists in mining maximal frequent itemsets (MFI) by extending the SmartMiner algorithm for the

intertransaction case. We have called the new algorithm InterTraSM (Inter Transaction Smart Miner).

Because it uses depth first search the memory needed by the algorithm is reduced; a strategy for passing tail

information for a node combined with a dynamic reordering heuristic lead to improved speed. Experiments

comparing InterTraSM to other existing algorithms for mining frequent intertransaction itemsets have

revealed a significant gain in performance. Further development ideas are also discussed.

1 INTRODUCTION

Association rule mining is a field of the data mining

domain that has developed extensively in the last

years. After the problem was introduced in

(Agrawal, Imielinski and Swami, 1993) and the A-

Priori algorithm was introduced in (Agrawal and

Srikant, 1994), the research expanded into a vast

number of directions. There have been proposed

other algorithms for the original problem, either

Apriori-like or with a new structure. Also new

algorithms have appeared for mining episodes and

sequential patterns, mining correlations, mining

generalized, multilevel or quantitative association

rules. Our algorithm contributes to another of these

new directions, mining intertransaction association

rules.

The initial association rule mining problem

ignored any correlation between the transactions and

searched for associations only between items inside

a transaction – we call this case intratransaction

analysis. To search for associations between items

across several transactions ordered on a dimension

(usually time or space), intertransaction association

rule mining has been used.

We use the stock market database example to

differentiate between intra- and inter- transaction

analysis. If the database contains the price for each

stock at the end of the trading day, an

intratransaction association rule might be “If stock

prices for companies A and B go up for one day,

there is a probability of over c% that the price for

company C will also go up the same day”. However,

analysts might be more interested in rules like “If

stock prices for companies A and B go up for one

day, there is a probability of over c% that the price

for company C will go up two days later.” This rule

describes a relationship between items from

different transactions, and it can be discovered only

by using intertransaction analysis.

Several algorithms for intertransactional

association rule mining have been introduced.

The E-Apriori (Extended Apriori) and EH-

Apriori (Extended Hash Apriori) algorithms have

been proposed by (Lu, Feng and Han, 2000). They

use the Apriori algorithm for mining frequent inter-

transaction itemsets. The EH-Apriori algorithm also

uses a hash in order to reduce the number of

candidate intertransaction itemsets with two

elements.

(Tung et al., 2003) developed FITI – an

algorithm that discovers first the frequent

intratransaction itemsets and then uses them to

generate the frequent inter-transaction itemsets.

The ITP-Miner algorithm from (Lee and Wang,

2007) uses a structure called dat-list to store item

information and an ITP-tree to store discovered

frequent inter-transaction patterns.

The EFP-Tree algorithm presented in (Luhr,

West and Venkatesh, 2007) is an extension of the

FP-Tree (Frequent Pattern Tree) algorithm for the

148

Ungureanu D. and Boicea A. (2008).

INTERTRASM - A Depth First Search Algorithm for Mining Intertransaction Association Rules.

In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 148-153

DOI: 10.5220/0001880701480153

 SciTePress

intertransaction case. It uses a divide-and-conquer

approach to avoid candidate generation.

In this paper we propose a new method for

mining frequent intertransaction itemsets called

InterTraSM. This algorithm is an extension for the

intertransactional case of the SmartMiner algorithm

presented in (Zou, Chu and Lu, 2002).

As the authors remark in the above mentioned

paper, mining frequent itemsets is infeasible when

the frequent patterns are long because of the

exponential number of frequent itemsets. An

alternative is mining maximal frequent itemsets

(MFI) – itemsets that are not a subset of any other

frequent itemset. Once we have obtained the MFI we

can easily obtain all the frequent itemsets, who can

then be counted for support in a single scan of the

database.

Like SmartMiner, InterTraSM uses a depth first

search (DFS) to determine maximal frequent

itemsets. It also uses a strategy for passing tail

information for a node combined with a dynamic

reordering heuristic that improve the speed of

execution.

The remainder of this paper is organized as

follows: in Section 2 we will give a formal definition

for the problem of intertransaction association rules

mining. In Section 3 we will describe our proposed

algorithm, InterTraSM. In Section 4 we will present

the experimental results we have obtained so far, and

we will present the conclusions and plans for future

work in Section 5.

2 PROBLEM DESCRIPTION

In this section we introduce some notations and we

present a formal definition for the problem of

mining intertransaction association rules.

Definition 2.1. Let I = {e

, e

, …, e

} be a set of

items and let D be an attribute with values within the

domain Dom(D). We call a transactional database a

database with transactions (records) of the form (d,

S), where d

∈ dom(D) and S ⊂ I.

We restrict our search for associations to a

maximum span of transactions, given as an input

parameter.

Definition 2.2. A sliding window W in a

transactional database T represents a set of

continuous intervals from the domain D, such that

there exists in T a transaction associated to the first

interval from W. Each interval from W is called a

subwindow of W, and they are numbered

corresponding to their temporal order d

, d

, ...,

. We also use the notation W[0], W[1], ..., W[m].

Definition 2.3. Let T be a transactional database, let

I be the set of items with n = | I| and let W be a

sliding window with w intervals. A megatransaction

M associated with W is the set

M = {e

(j) | e

∈

W[j], 1 ≤ i ≤ n, 0 ≤ j ≤ w-1}.

Items from a megatransaction will be called from

now on extended items.

Let E be the set of all possible extended items

E = {e

(0), e

(1), …, e

(w-1), e

(0), …,

(w-1)}

We call an intratransaction itemset a set of items

⊂ I. We call an intertransaction itemset a set of

extended items B

⊂ E that contains at least an

extended item e

(0), with 1 ≤ i ≤ n.

Definition 2.4. An inter-transaction association rule

has the form X -> Y, where:

i) X, Y

⊂ E

ii) There is at least one element e

(0)

in X, 1

≤ i ≤ n

iii) There is at least one element e

(j)

in Y, 1

≤ i ≤ n, 1 ≤ j ≤ w-1

iv) X and Y are disjoint

Let T

be the set of megatransactions that

contain the set X

∪ Y, let T

be the set of

megatransactions that contain the set X and let N be

the total number of transactions.

Then S = | T

| / N and C = | T

| / |T

| are

the support and confidence for the intertransaction

association rule.

As in the classical case, the problem of mining

intertransaction association rules can be divided in

two parts:

- finding the frequent itemsets

- generating the association rules.

The second problem takes much less

computational time than the first one, so it presents

little interest for research. A solution has been

discussed for example in (Tung et al., 2003). Our

algorithm (like the algorithms mentioned before)

will therefore focus on a solution for the first

problem.

INTERTRASM - A Depth First Search Algorithm for Mining Intertransaction Association Rules

149

3 ALGORITHM DESCRIPTION

We now introduce the InterTraSM algorithm. As we

mentioned before, InterTraSM is an adaptation of

the SmartMiner algorithm described in (Zou, Chu

and Lu, 2002) for intertransaction association rule

mining. Therefore the theoretical foundations of the

two algorithms are very similar. Our main

contribution has been to identify intertransaction

mining as a domain where searching for MFI would

lead to an improvement in performance, and to apply

and customize the existing algorithm to the

intertransaction analysis case; we also provided a

new implementation.

InterTraSM finds maximal frequent itemsets

(MFI) of extended items from a transactional

database. The algorithm uses depth first search and

for performance optimization it uses a dynamic

reordering to eliminate infrequent items from the tail

of a current node. A hash table is also used to save

the itemsets discovered as frequent at node-level, in

order not to go down a tree path that was already

investigated while exploring a maximal frequent

itemset.

As we mentioned the algorithm performs a depth

first search, so at any step it works on a node from a

search tree. We describe below the data managed at

the level of a node used by the algorithm and how

the data is processed.

A node N is identified as X:Y, where X (the

head) is the set of items that have been discovered to

be part of a frequent itemset, and Y (the tail) is the

set of items that still have to be explored. The

purpose of the node is to find maximal frequent

itemsets in the transaction set T(X) – all the

transactions that include X.

The starting node is

Φ :E (the empty set and the

set of all the possible extended items).

The entry data for a node are:

- the transaction set T(X)

- the tail Y

- the global data information Ginf, which is the

tail information for the node known so far

(this contains the itemsets that have been

discovered in a previous step to be frequent

in T(X)).

The exit data for a node are:

- the updated GInf

- the discovered maximum frequent itemsets

Mfi.

The data processing at a node N is described

below:

- count the support for each item from Y in the

transaction set T(X)

- remove the infrequent items

- while (Y has at least one element)

- select from Y an item a

to be the head of

the next state S

- Y

1+i

= Y – a

will be the tail for S

1+i

- obtain the auxiliary tail information for

1+i

by projecting on Y

the itemsets that

contain a

from the tail information Ginf.

- recursively call the algorithm for the node

1+i

= Xa

: Y

1+i

. The returned values will

be Mfi

and the updated tail information.

- Y = Y

1+i

- end (while)

The processing of the node returns the maximal

frequent itemsets to be Mfi =

∪

Mfi

, and the

updated Ginf as the itemsets in the original Ginf that

have not been marked as deleted.

As we mentioned, InterTraSM uses extended

items instead of the intratransaction items used by

SmartMiner. A customization for this case is that the

first node we select while searching in depth from

the root of the tree corresponds only with items from

the first interval (interval 0). This was done because

each frequent itemset has to have at least an item

from interval 0.

We created our own implementation of the

algorithm using C, with a structure similar to the one

for the SmartMiner algorithm described in (Zou,

Chu and Lu, 2002) – but with modifications for the

intertransaction case (The SmartMiner algorithm

was implemented in Java). We felt that writing the

algorithm in C enabled us to better control the

memory use of the algorithm.

4 PERFORMANCE STUDY

We used both synthetic data and real data to evaluate

the performance of the algorithm.

To generate the synthetic data we used the same

generator as the one described in (Luhr, West and

Venkatesh, 2007) to evaluate EFP-Tree, gracefully

provided to us by the authors. It uses the same

method as the one used to evaluate FITI and ITP-

Miner.

The real data consists of two datasets, WINNER

and LOSER, similar to those used in (Lee and

ICSOFT 2008 - International Conference on Software and Data Technologies

150

Wang, 2007). They have been obtained from the

values of ten stock exchange indexes from January

1, 1991 to December 31, 2005. In the WINNER set a

transaction for a trading day contains the stock

indices that rise for the day, and in the LOSER set

we have the stock indices that fall. The stock indices

used are the ASX All Ordinaries Index (ASX),

CAC40 Index (CAC), DAX Index (DAX), Dow

Jones Index (DOW), FT-SE 100 Index (FTS), Hang

Seng Index (HSI), NASDAQ Index (NDQ), Nikkei

225 Index (NKY), Swiss Market Index (SMI), and

Singapore ST Index (STI).

Two synthetic data sets representing sparse and

dense data were generated, with parameters identical

to those used in the evaluation of EFP-Tree.

Table 1 lists the parameters used to create the

data sets used in the experimentation.

Table 1: Parameters used in the generation of the synthetic

data sets.

Parameter Sparse Dense

Number of intratransactions

Size of the intertransaction pool

Average length of intratransactions

Maximum length of intratransactions

Average length of intertransactions

Maximum length of intertransactions

Maximum number of unique items

Maximum interval span of

intertransactions

500

200

100

The program was benchmarked under a

Microsoft Windows XP OS, on a PC with Intel

Pentium IV CPU with speed of 3GHz and main

memory of 1GB. The code has been written and

compiled using Microsoft Visual Studio 2003.

Since FITI has been shown to be more

computationally efficient than EH-Apriori and both

EFP-Tree and ITP-Miner have been shown to

outperform FITI, we have only made comparisons

with EFP-Tree and ITP-Miner.

We have compared the execution times of

InterTraSM on the synthetic data sets with the

execution times reported for EFP-Tree in (Luhr,

West and Venkatesh, 2007) for synthetic data

generated with the same parameters by the same

generator (probably different actual data though,

since it is a random generator).

For the synthetic sparse data set we have

gradually lowered the support threshold from 1.6%

to 0.6%, using a fixed intertransaction window size

of 4. For the synthetic dense data set we have

gradually lowered the support threshold from 13% to

8%, using a fixed intertransaction window size of 6.

The execution times for InterTraSM are displayed in

Figure 1 (sparse data) and Figure 2 (dense data).

We have then incremented the intertransaction

window size from w=0 to w=10 with fixed

minimum supports of 1% for the sparse data and

10% for the dense data. The results are displayed in

Figure 3 (sparse data) and Figure 4 (dense data).

Figure 1: Minimum support versus runtime, sparse data

set, with maxspan=4.

Figure 2: Minimum support versus runtime, dense data set,

with maxspan=6.

Figure 3: Intertransaction window size versus runtime,

sparse data set, with support=1%.

INTERTRASM - A Depth First Search Algorithm for Mining Intertransaction Association Rules

151

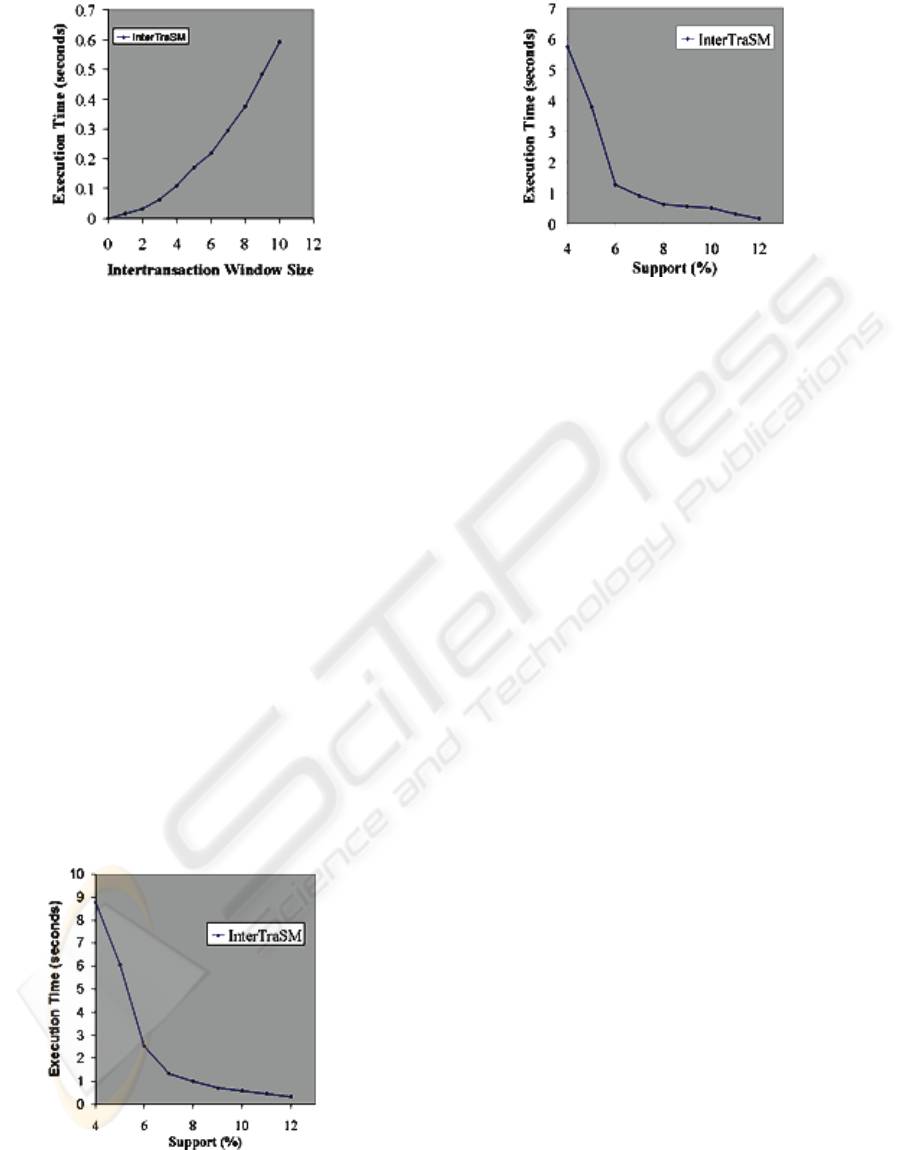
Figure 4: Intertransaction window size versus runtime,

dense data set, with support=1%

We can see that all the execution times

displayed in these charts are under one second,

while the execution times reported for the EFP-

Tree in (Luhr, West and Venkatesh, 2007) for

synthetic data generated with the same parameters

have values of tens, even hundreds of seconds.

Since the processors used have similar

performances, even accounting for the different

implementation languages (C versus Ruby),

InterTraSM seems to perform at least an order of

magnitude better than EFP-Tree.

We have compared the execution times of

InterTraSM on the real data sets with the execution

times reported for ITP-Miner on transactions

obtained from the same stock indices values.

For both the WINNER and LOSER datasets we

have used an intertransaction window size of 4 and

we have varied the minimum support threshold

from 4% to 12%. The results are displayed in

Figure 5 (WINNER data set) and Figure 6 (LOSER

data set).

Figure 5: Minimum support versus runtime, WINNER

data set, with maxspan=4.

Figure 6: Minimum support versus runtime, LOSER data

set, with maxspan=4.

Comparing the results with those reported for

running ITP-Miner on the same data sets in (Lee

and Wang, 2007), on a processor with similar

performances using Microsoft Visual C++ 6.0, it

seems that there is an order of magnitude

difference in favor of InterTraSM, especially when

the minimum support value decreases. For example

on the LOSER data set with the support threshold

at 4% InterTraSM takes less than 6 seconds, while

the authors reported the ITP-Miner takes about 100

seconds.

5 CONCLUSIONS

In this paper we have proposed a new algorithm for

mining intertransaction association rules called

InterTraSM, an extension of the SmartMiner

algorithm for the intertransaction case. InterTraSM

uses depth first search and mines for maximal

frequent itemsets (from which all the frequent

itemsets can be easily generated). Previous

algorithms have mined for all the frequent itemsets

and they thus have had to count support for an

exponentially large number of frequent itemsets

compared to our algorithm. Experiments with

similar data and on similar machines to those used

for evaluating EFP-Tree and ITP-Miner have

shown that InterTraSM outperforms them by at

least an order of magnitude, especially when the

minimum support threshold is reduced – generating

longer maximal frequent itemsets.

In our future research we want to apply the

algorithm to some more real data sets and see how

it performs. We also want to extend the algorithm

from 1-dimensional to n-dimensional transactional

databases.

ICSOFT 2008 - International Conference on Software and Data Technologies

152

REFERENCES

Agrawal, R., Imielinski, T., Swami, A., 1993. Mining

Association Rules Between Sets of Items in Large

Databases. In Proc. of the ACM SIGMOD Conference

on Management of Data.

Agrawal, R., Srikant, R., 1994. Fast Algorithms for

Mining Association Rules. In Proc. of the 20th Int'l

Conference on Very Large Databases.

Lu, H., Feng, L., Han, J., 2000. Beyond intratransaction

association analysis: mining multidimensional inter-

transaction association rules. In ACM Transactions on

Information Systems. Volume 18 , Issue 4.

Tung, A.K.H., Lu, H., Feng, L., Han, J., 2003. Efficient

mining of intertransaction association rules. In IEEE

Transactions on Knowledge and Data Engineering.

Volume 15, Issue 1.

Lee, A.J.T., Wang, C-S., 2007. An efficient algorithm for

mining frequent inter-transaction patterns. In

Information Sciences: an International Journal.

Volume 177, Issue 17.

Lühr, S., West, G., Venkatesh, S., 2007. Recognition of

emergent human behaviour in a smart home: A data

mining approach. In Pervasive and Mobile

Computing. Volume 3, Issue 2.

Zou, Q., Chu, W., Lu, B., 2002. SmartMiner: a depth first

algorithm guided by tail information for mining

maximal frequent itemsets. In Proc. of the 2002 IEEE

International Conference on Data Mining.

INTERTRASM - A Depth First Search Algorithm for Mining Intertransaction Association Rules

153