FAULTS ANALYSIS IN DISTRIBUTED SYSTEMS

Quantitative Estimation of Reliability and Resource Requirements

Christian Dauer Thorenfeldt Sellberg

IBM Denmark A/S. Nymoellevej 91, 2800 Kgs. Lyngby, Denmark

Michael R. Hansen, Paul Fischer

Institute of Mathematical Modelling, Technical University of Denmark

Richard Petersens Plads, DTU - Building 321, 2800 Kgs. Lyngby, Denmark

Keywords: Fault tolerance, Dependable systems, Distributed systems, Process Algebra, Pi-calculus.

Abstract: We live in a time where we become ever more dependent on distributed computing. Predictable quantitative

properties of reliability and resource requirements of these systems are of outmost importance. But today

quantitative properties of these systems can only be established after the systems are implemented and

released for test, at which point problems can be costly and time consuming to solve. We present a new

method, a process algebra and simulation tool for estimating quantitative properties of reliability and

resource requirements of a distributed system with complex behaviour hereunder complex fault-tolerance

behaviour. The simulation tool allows tailored fault injection e.g. random failure and attacks. The method is

based upon π-calculus (Milner, 1999) to which it adds a stochastic fail-able process group construct.

Performance is quantitatively estimated using reaction rates (Priami, 1995). We show how to model and

estimate quantitative properties of a CPU scavenging grid with fault-tolerance. To emphasize the

expressiveness of our language called Gπ we provide design patterns for encoding higher-order functions,

object-oriented classes, process translocation, conditional loops and conditional control flow. The design

patterns are used to implement linked lists, higher-order list functions and binary algebra. The focus of the

paper--is—on--practical--application.

1 INTRODUCTION

Failure (faults) happens. The computational

resources of distributed systems are unreliable; as

every human made thing is and they will eventually

fail either because of random failure, because of

limited longevity or because of malicious attacks. To

be reliable then dependable systems need to be

robust against these different causes of failure.

Robustness against failures can e.g. be achieved via

fault-tolerance techniques.

Analysis of reliability and resource requirements

(such as performance) is usually delayed (or not

done at all) until a distributed system is implemented

and deployed, where the analysis is based on data

collected via load and stress testing, LST, of the

deployed system via LST tools. The reason for this

delay is that reliability and resource requirements of

a system are not easily deduced in the planning and

modelling phases. We need a method which allows

quantitative estimation of reliability and quantitative

estimation of predictive statistics (mean, standard

deviation, minimum, median, maximum) of resource

requirements in space and time (e.g. memory,

network size, workload, performance) based on a

model of the system. The method should be able to

account for location failure (e.g. server crash) and

fault-tolerance (fault detection, fault confinement,

fault recovery) techniques. The method should be

able to express component based job distribution to

a computational resource. Our thesis is that π-

calculus (Milner, 1999) could be extended for this

purpose and the results presented in this paper are a

summary of the results from the master thesis

(Sellberg, 2008).

Why a new process algebra? There exists

process algebras based on π-calculus (Milner, 1999)

with location failure; examples are asynchronous π

Dauer Thorenfeldt Sellberg C., R. Hansen M. and Fischer P. (2008).

FAULTS ANALYSIS IN DISTRIBUTED SYSTEMS - Quantitative Estimation of Reliability and Resource Requirements.

In Proceedings of the Third International Conference on Software and Data Technologies - SE/GSDCA/MUSE, pages 45-52

DOI: 10.5220/0001881700450052

 SciTePress

(Amadio, 1997) and DπLoc, (Francalanza, 2006).

But these process algebras have no means for

expressing quantitative aspects of reliability and

resource requirements in time and space. One

extension of π-calculus with quantitative properties

is Stochastic π-calculus, Sπ, (Priami, 1995). Sπ can

via its stochastic reaction rate extension to π-

calculus quantify system performance but Sπ has no

notion of failure.

We have considered whether we should extend

e.g. π

or DπLoc with quantitative properties but

have abandoned doing this for the following reasons.

and DπLoc has fault detection logic, FD, a ping

“are you alive” construct, as a part of the syntax. FD

in π

and DπLoc cannot fail, unlike FD in real

systems (see Section 2), so we cannot use π

and

DπLoc to study fault detection. Another issue is that

and DπLoc have syntactical fault injection

constructs. We prefer for clarity reasons that a model

is defining a system’s functional specification,

which does not include fault injection logic.

Therefore we introduce a new (π-calculus based)

process algebra which is able to express “location

failure” and quantitative properties of reliability and

resource requirements in time and space. Our

process algebra, named Gπ-calculus, adds to π-

calculus a stochastic fail-able process group

construct for location failure. We adapt reaction

rates from (Priami, 1995) in the form of transition

time labels (see section 3) for quantitative estimation

of performance. Component based job distribution is

expressed via a distribution rule. The semantics of

Gπ is given in the form of a structural operational

semantics (Plotkin, 1981). The emphasis will,

however, be on practical applications.

The paper has the following outline. In Section 2,

we present a motivating example and give a flavour

of how the method quantitatively can estimate

reliability and descriptive statistics of resource

requirements in time and space of a simple CPU

scavenging grid. Technical details are left to Section

6. In Section 3, we give an informal introduction to

Gπ-calculus. In Section 4 we stress the

expressiveness of Gπ by presenting design patterns

for how to use it to implement advanced behaviour.

In Section 5, we present the simulator tool which

can estimate descriptive statistics of quantitative

properties of models. In Section 6 we introduce how

to model fault-tolerance techniques by elaborating

on the example from Section 2. The paper ends with

a conclusion.

2 A MOTIVATING EXAMPLE

Dependability on a system requires that the system

has predictable reliability and predictable

quantitative resource requirements in time,

(performance), and space, e.g. network size (here

defined as the number of concurrent computers

which simultaneously is having a job assigned),

number of job distributions (the number of

assignments of a computational problem to a new

computational resource) and workload (here defined

as the number of computations/reductions). With

predictable we understand that standard deviation is

relatively low in respect to the mean and that min

and max is relatively close to the mean. We define

reliability of a system as the probability that a

system service will answer an arbitrary request in

accordance with its system specification.

We shall consider an example, a volunteering

CPU grid, CPU-GRID, from High Performance

Computing. High Performance Computing, HPC, is

today applied in solving complex computation

intensive problems. One way to achieve HPC is via

a CPU-GRID. Examples of CPU-GRIDs are:

folding@- home, seti@home and world, community

grid which respectively have the following urls:

 http://folding.stanford.edu/

 http://setiathome.berkeley.edu/

 http://www.worldcommunitygrid.org

A CPU-GRID is in its simplest form based on a

central computer, a grid master, which has a set of

volunteering computers, CPUs, to which it can

delegate/schedule computational problems.

Volunteering computers can usually join the grid by

downloading and installing a screensaver which will

connect the volunteering computer to the grid. When

a grid master receives a job request by a grid user it

will usually break the job request into sub-problems

which it will delegate to volunteering CPUs. When a

sub-problem is solved the volunteer CPU will return

the sub-result to the grid master. The grid master

will assemble all sub-results into one final result and

return it to the user. The owner of a volunteer CPU

can at any time chose to (temporarily or indefinitely)

disconnect his CPU from the grid. From the point of

view of the grid master then this disconnection can

be considered as the failure of the sub-problem

delegated to that CPU. To insure that the CPU-

GRID can achieve reliable computing with such

unreliable computational resources it needs a fault-

tolerance strategy for handling the failure of

volunteering CPUs.

ICSOFT 2008 - International Conference on Software and Data Technologies

Fault-tolerance is about fault detection, fault

isolation/error assessment and fault recovery/error

correction (Tanenbaum, 2006). Fault detection in

distributed processes is achieved by timed processes,

usually called watchdogs, triggering timed e.g. “are-

you-alive” signals to a heart-beat process located at

a component under fault surveillance, e.g. a

volunteering CPU. If a timed heart-beat is missed

then a watchdog will handle it as the failure of the

volunteering CPU. The watchdog will then trigger

fault recovery by rescheduling the failed sub-

problem. This is the fault-tolerance approach

followed in our example below. Notice that race

conditions can course a heart-beat to be missed. This

will falsely trigger fault recovery and reschedule an

already ongoing job.

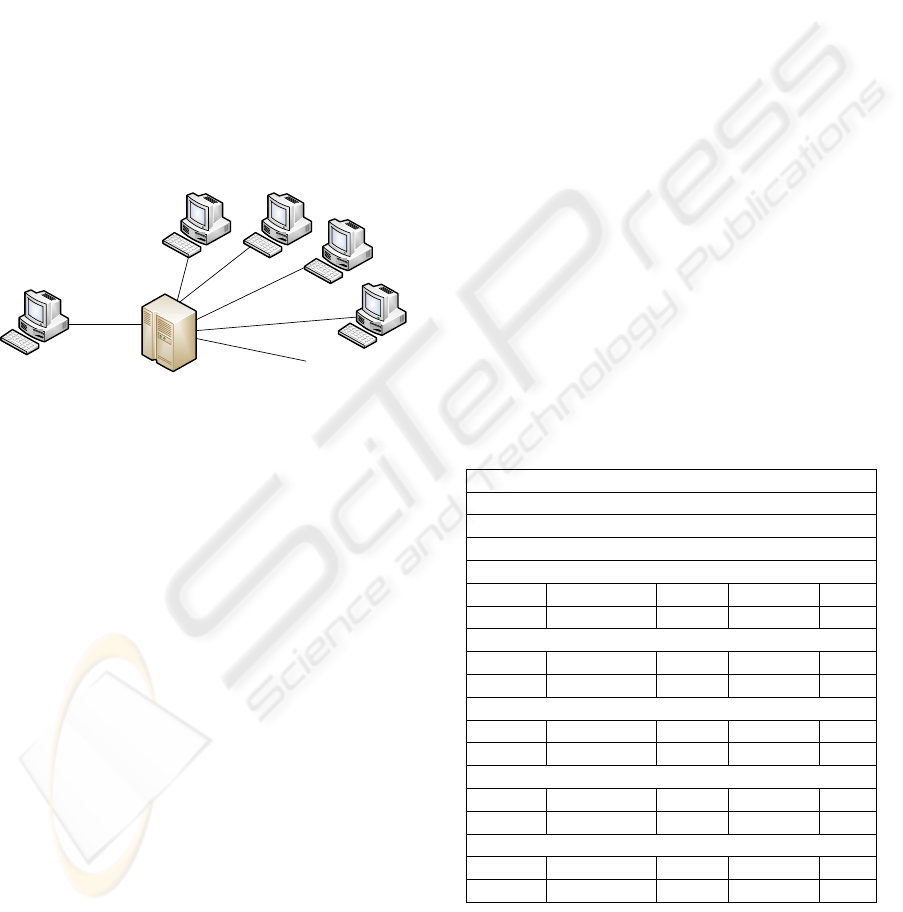
The architecture of the CPU-GRID example is

shown in Figure 1.

Figure 1: CPU-GRID architecture.

The CPU-GRID consists of a grid master and an

unlimited amount of volunteering CPUs. The user

entrance to the grid is via the grid master. The grid

master can receive a job request from a user which it

split into two sub-problems A and B which it will

schedule to volunteering CPUs. A CPU which has

been assigned a job of type A or B will be named

CpuA and CpuB resepectively. The grid master will

apply passive task replication as its fault-tolerance

strategy, i.e. it will apply watchdogs at the grid

master and heart-beat listening processes at CpuA

and CpuB for fault detection and fault recovery. The

failure probability of CpuA and CpuB is 0.5, i.e.

they are very unreliable. We consider the grid master

to have failure probability 0, i.e. it cannot fail.

We have modelled this example in Gπ and

experimented with the simulator tool. Table 1 shows

the results.

Reliability and performance are two system

properties being perceived by the grid user. The

model has high reliability but its performance is

unpredictable (standard deviation, std.dev Table 1, is

large compared to the mean) and from the point of

view of the grid user this unpredictability makes the

grid undependable.

“Network size”, “Number of job distributions”

and “System workload” are parts of the system

resources which need to be available for the CPU-

GRID for it to deliver the estimated reliability and

performance. The results show that these resource

requirements are unpredictable, but whether this

unpredictability indicates a dependability problem

depends on the actual resources available to the

CPU-GRID. If the CPU-GRID had access to e.g.

600000 volunteering computers then the resource

requirement unpredictability would probably be of

no concern but if the CPU-GRID had access to only

100 computers then it would be of concern.

The statistics for network size (Table 1) give us

an indication of the “quality” of the fault-tolerance

strategy. We can derive that fault detection wrongly

triggers fault recovery of non-failed components

because network size would be no larger than 4 (1

user, 1 grid master, 1 CpuA, 1 CpuB) if fault

detection did not fail but network size (Table 1,

Network size) is on average 7.75 and can be as large

as 16 concur rent computers.

Faults, is the number of failed volunteering

computers and can be interpreted as the “hostility”

of the environment. It seems fair to say that the

environment is relatively hostile.

Table 1: CPU scaveng. grid with passive task replication.

Total number of experiments

100.0

Reliability

1.0

Performance (times units)

mean std.dev. min median max

695,41 461,9111 49 583,5 2114

Network size

mean std.dev. min median max

7,75 2,2036 5 7 16

Number of job distributions

mean std.dev. min median max

275,72 183,368 22 229 848

System workload (reductions)

mean std.dev. min median max

2196,54 1457,3966 160 1785 6685

Faults

mean std.dev. min median max

269,52 182,1981 17 222,5 841

GridMaster

CPU

User

CPU

...

Unlimited number of

volunteering CPUs

FAULTS ANALYSIS IN DISTRIBUTED SYSTEMS - Quantitative Estimation of Reliability and Resource Requirements

Table 2: Structural Operational Semantics of Gπ-calculus.

Failure rules

1. […+x!y.P]

θi

| […+x?z.R]

θj

→

σi*(1-σj), ρ

0 | […+x?z.R]

θj

2. […+x?y.P]i

θi

| […+x!z.R]

θj

→

σi*(1-σj), ρ

0 | […+x!z.R ]

θj

3. […+x!y.P]

θi

| […+x?z.R]

θj

→

σi*σr, ρ

0 | 0

4. […+x!y.P]

θi

| …+x?z.R →

σi, ρ

0 | …+x?z.R

5. […+x?y.P ]

θi

| …+x!z.R →

σi, ρ

0 | …+x!z.R

6. […x!y.P | ...+x?z.Q]

θi

→

σi, ρ

Communication rules

1. […+x!y.P]

θi

| […+x?z.R]

θj

→

(1-σi)*(1 - σj), ρ

[P]

θi

| [R{y/z}]

θj

2. […+x!y.P ]

θi

| …+x?z.R →

(1-σi), ρ

[P]

θi

| R{y/z}

3. […+x?y.P ]

θi

| …+x!z.R →

(1-σi), ρ

[P{z/y}]

θi

| R

4. […+x!y.P | …+x?z.R]i

θi

→

(1-σi), ρ

[P | R{y/z}]

θi

…+x!y.P | …+x?z.R →

σ=1, ρ

P | R{z/y}

Distribution rule

[(new a1…an)(Q | [P]

θj

)]

θi

→

σ,ρ

(new a1…an)( [Q]

θi

| [P]

θj

) where σ=1 and ρ=0

3 INTRODUCTION TO

Gπ-CALCULUS

The calculus Gπ is based on the π-calculus

introduced in (Milner, 1999) for modelling and

analysing concurrent, communicating and mobile

processes. For a comprehensive introduction to π-

calculus we refer to (Milner, 1999) or (Sangiorgi,

2001). The syntax of π-calculus is shown in Table 3.

Table 3: π-calculus syntax.

P,Q ::= S | *P | (new x) P | P|Q | 0

S, T ::= α.P | S + T

α ::= a?b | a!b

See Table 4 for an explanation of terms used.

Table 4: Gπ-calculus syntax.

P,Q ::= S | *P | (new x) P | P|Q | 0 | [P]θ

S, T ::= α.P | S + T

α ::= a?b | a!b

θ ::= ε | ‘@’ name=value ‘;’ θ

Where ε is the empty string. P and Q are processes,

S and T are summations and α is an action. The

syntactic constructs have the following meaning.

π-calculus is Turing complete and therefore

allows the modelling of arbitrarily complex

behaviour, but π-calculus cannot express

quantitative properties as reliability and resource

requirements in time and space or grouped process

failure and therefore primitives to express that is

added to π-calculus.

The syntax of Gπ is given in Table 4 and the

operational semantics is sketched in Table 2.

Composition: P|Q means that P and Q are two

concurrent processes.

Prefix: α.P means sequencing of behaviour. The

process can engage in an α action and then it

behaves as P.

Action: a?b and a!b are symbolizing

communication points. a?b is an input action and a!b

is and output action. The name, a in a?b and a!b is

called the subject and b is called the object. When an

input- and output-action have the same subject-name

they can engage in communication (Table 2,

communication rules).

Summation: S + T means choice of process

behaviour where only one alternative i.e. either S or

T but nor both will evaluate, the other alternative is

discarded.

Replication: *P represents an infinite set of

process P occurrences. We have the following

structural congruence rule *P ≡ P | *P.

Restriction: (new x) P means that x is bounded in

P. In the following example (new x)(P) | (new x)(Q)

then the x’s in P and Q represents two different

names.

Termination: 0 means a terminated process, a

process that takes no action.

Grouping: [P]

means process grouping. The

process group can evaluate to the null process,

[P]

→0 (Table 2, failure rules). The tagging θ is a

convenient way of adding meta information to

process groupings. We use the tag @pf=0.5; for

example to indicate the failure probability of a

process group. We shall se other kinds of tags for

type in section 6.

ICSOFT 2008 - International Conference on Software and Data Technologies

We will now briefly explain the reason for our

failure modelling approach. The processes deployed

on a computational resource are un-reliable because

a computational resource always can fail given some

probability. The processes, so-to-speak, “inherit”

this unreliability from their computational resource,

because they cease to exist with the computational

resource. We model a computational resource by a

process group construct, [P], which we add as an

extension to the π-calculus syntax (Table 4). We

model the unreliability of the computational

resource by extending the reduction rules of π-

calculus with reduction rules of failure (Table 2).

Notice that failure is only defined for process

groups, [ ], having processes which can react; this

insures that we are only studying interesting failures

which affects behaviour.

In the operational semantics, each transition

arrow, →

σ, ρ

, has two labels. The first label, σ, is the

transition probability and the second, ρ, is the

transition time. The symbols σi and σj (Table 2) are

the probabilities that respectively the process group

marked i and j will fail during reaction. The

transition probability σi*(1-σj) is the probability for

the event that the process group marked i but not the

process group marked j will fail during reaction

(Table 2) etc. Using these transition labels we can

deduce transition path probabilities and transition

path times, to estimate reliability and performance

figures.

The semantic reduction rules for communication

trivially specify that communication will take place

when none of the involved process groups fails and

the transition probabilities are reflecting this. Job

distribution or assignment to computational

resources is specified by the distribution.

Different aspects of process size are used to

estimate resource requirements in e.g. memory and

network size. The number of times the different

reduction rules are applied is used to estimate

different aspects of work load, e.g. network traffic

and CPU load.

4 EXPRESSIVENESS

To make Gπ useable by a wide audience we have

presented six design patterns, Gπ-patterns (Table 5),

for how Gπ-calculus can be used to implement

complex behaviour via concepts familiar from the

functional or object oriented world.

The design patterns have been heavily inspired

by both (Milner, 1999) and (Sangiorgi, 2003). Each

design pattern has a name for reference, it defines a

problem or problem context where it is useful, it

defines a set of terms to be used as a vocabulary for

talking about the pattern and most importantly it

defines a Gπ process structure as a solution to the

problem. The intention is that these process

structures are to be used as coding templates which

can be modified to fit a concrete problem. We will,

for space reasons, not go into details about how

these high-level constructs can be expressed in Gπ.

Table 5: Gπ patterns overview

Pattern Problem context

Gπ-Function

Need for an implementation

of a function as known from

functional programming

Gπ-Conditional-

Loop

Need for conditional loop e.g.

do-while

Gπ-If-Equals-Then-

Else

Need for conditional control

flow

G-Higher-Order-

Function

Need for higher order

functions or subroutines.

Gπ-Class-Object

Need for an object oriented

approach

Gπ-Process-Group-

Handle

Need for process

translocation between process

groups

To demonstrate the usefulness of the Gπ-patterns

we have used them to implement Gπ functionality

on a representation of 7 bit binary numbers. All Gπ

implementations have been tested via the simulator

tool. We have implemented binary algebraic

functionality where e.g. the implementation of

binary addition makes use of the Gπ-Function, Gπ-

Conditional-Loop and Gπ-Conditional-Control-Flow

patterns. Our Gπ implementation of binary

multiplication makes among others use of the binary

addition implementation via the Gπ-Higher-Order-

Function pattern.

We have implemented linked list of binary

numbers, where each list node is implemented as an

instance of the Gπ-Class-Object pattern. The

implementation of the linked list implements object

functionality (methods) for traversing the list and for

updating the value of a specific node and for adding

new elements to the list. We have implemented

higher-order linked list function which can apply a

function to each element in the list.

The implemented Gπ functions can be

considered as the beginning of a reusable Gπ-API.

FAULTS ANALYSIS IN DISTRIBUTED SYSTEMS - Quantitative Estimation of Reliability and Resource Requirements

5 SIMULATOR TOOL

The simulator tool is written in Java. It has a

graphical user interface, GUI, and a command line

interface. The simulator has two main functions. It

has an interface for studying the behaviour of a Gπ-

model; A Gπ-model can be loaded into the simulator

and the user can study the behaviour of the model by

observing structural changes in the model by

applying one reduction rule at the time. The other

function is that it can be used to quantitatively

estimate reliability and descriptive statistics of

resource requirements in time and space of a Gπ-

model.

The simulator is an interpreter of the structural

operational semantics of Gπ. It reduces a Gπ model

one reduction rule at the time. After each reduction

step it collects and updates quantitative properties of

the Gπ model.

We call one execution of the simulator algorithm

on a Gπ-model for a simulation experiment. For

each simulation experiment we collect quantitative

properties. We can specify to the simulator (not

shown here, please assist (Sellberg, 2008)) what a

successful outcome is, so the simulator can decide

whether a simulation experiment was a success or

not (step number 07 in the simulator algorithm

below). This is used to estimate reliability. The

estimator part of the simulator tool will run a

simulation experiment a specified number of times

and collect quantitative properties and calculate

descriptive statistics. Reliability is estimated as the

fraction of successful simulation experiments.

Pseudo code for the simulator algorithm is given

below where the symbol Γ symbolizes the Gπ-model

to be executed.

simulate( Γ)

01: distribute (un-nest) all nested

process groups in Γ

02: randomly find matching process pair

in Γ which can react

03: if no match is found then stop else

continue

04: apply fault injection logic

05: if faults were injected then goto

step 01 else continue

06: apply reaction for found matching

process pair in Γ

07: test if a functional test evaluated

with success. If true then stop

else goto step 01

The fault injection logic and reaction rate logic is

delegated to interfaces which can be implemented to

fit specific failure and reaction rate scenarios. A Gπ

model is given as ASCII text to the simulator.

The purpose of Figure 2 and Figure 3 is to give

the reader an impression of the estimator part of the

simulators GUI.

Figure 2 shows the Gπ-model of the CPU

scavenging grid loaded from an ASCII file into the

simulator GUI. We can edit the model (and save

changes) via the black editor screen (Figure 2).

Figure 2: Gπ-model loaded into the simulator tool.

We can enter the number of simulation

experiments we want to base our estimation results

on and initiate our estimation process by pressing

the button “run estimation”. Estimation results are

presented as shown in Figure 3 and show the

estimated statistics of reliability and resource

requirements in time and space. The results have the

form presented in Table 1.

Figure 3: Result of executing a simulation.

ICSOFT 2008 - International Conference on Software and Data Technologies

6 FAULT-TOLERANCE

In (Sellberg, 2008) we sketch how we can use Gπ to

model relevant and interesting fault and fault-

tolerance behaviour. We show how to model

location failure, link failure and lost messages. We

sketch how we can model the failure scenarios

random failure, limited longevity and failures caused

by attacks. We show how we can model hot task

replication, passive task replication and voting based

fault-tolerance (Tanenbaum, 2006). We apply the

techniques to model and estimate quantitative

properties of a CPU scavenging grid with hot task

replication and passive task replication (the example

presented in Section 2) using fault detection, timers,

observer/watchdog, hearts-beats etc.

The architecture (see Figure 1) of the system in

Section 2 has the following basic and concurrent

process group (for the user, the grid master and the

two CPUs) structure in Gπ.

[...]@type=user; |

[...]@type=gridMaster;|

[...]@type=cpuA; |

[...]@type=cpuB;

The dots, ... , represents the business logic

specified in Section 2 including fault-tolerance logic.

We here just give a flavour of how we have

modelled fault-tolerance techniques in Gπ. The

complete model of the CPU scavenging grid of

Section 2 is in (Sellberg, 2008). We show how we

have implemented fault detection (via watchdogs,

heart-beats) and fault recover.

Timers are crucial so first we will show how we

can implement timers.

*init?¤.((new c)(

c!¤.c!¤.c!¤ |

c?¤.c?¤.c?¤.timeout!¤.init!¤

)) |

init!¤

The timer is a replication, because of the star *,

and the timer is initiated by a reaction between init?¤

and init!¤. The actual timing process is constituted

by the process

c!¤.c!¤.c!¤ |

c?¤.c?¤.c?¤.timeout!¤.init!¤.

The timing process captures the passing of time

via the reductions between c!¤ and c?¤. This will

work because our use of reaction rates insures that

each reduction takes a well defined amount of time.

After three reductions of c!¤ and c?¤., we have the

timeout event, timeout!¤.init!¤. When the timeout!¤

reacts then it reduces to init!¤ which will initiate a

new timing process.

The timer is used to implement fault detection by

pushing “are you alive” signals. A process group

under failure surveillance is equipped with a heart

beat listening process, *areYouAlive?¤. Part of the

fault detection logic of the watchdog process is as

follows.

*faultDetection?¤.(

areYouAlive!¤.timeout?¤.

faultDetection!¤

timeout?¤.failure!¤ )|

faultDetection!¤

Notice that the body of the fault-detection

process is a choice (due to the + symbol). I.e. it can

either evaluate to

areYouAlive!¤.timeout?¤.

faultDetection!¤

or to

timeout?¤.failure!¤

but not both. Also notice that the fault detection

process is a replication because of the star symbol *.

The fault detection process is initiated by the

reaction between faultDetection?¤ and

faultDetection!¤.

If the,

areYouAlive!¤.timeout?¤.

faultDetection!¤

process does not react with the heart beat

listening process before the timeout event, then the

failure observing process would evaluate to,

failure!¤, which can be used to trigger fault

recovery. If it does react then it will evaluate to

timeout?¤.faultDetection!¤, which again on timeout

will evaluate to faultDetection!¤ which will restart

the fault detection process.

Before we show the fault recovery process we

need to show how we implement job distribution.

The sketch of a volunteering CPU with a heart-beat

listening process is.

[*areYouAlive?¤|...]@type=cpuA;@pf=0.5;

The three dots is symbolising non-fault detection

related logic. The tag, @type=cpuA; is telling us that

this process group is modelling a CpuA. The tag,

@pf=0.5; is an instruction to the simulator that this

process has a probability of failure of 0.5 and will be

used by the fault injection logic.

The event failure!¤ from the fault detection

process presented previously can trigger fault

FAULTS ANALYSIS IN DISTRIBUTED SYSTEMS - Quantitative Estimation of Reliability and Resource Requirements

recovery via a fault recovery process of the

following form

*failure?¤.(

[*areYouAlive?¤ | ... ]@cpu=a;@pf=0.5;)

Notice that the fault recovering process is a

replication symbolized by the star symbol *. When

the process above reacts with failure!¤ it will

evaluate to [*areYouAlive?¤ | ... ]@cpu=a;@pf=0.5;

which is our notion of job-distribution or job-

assignment to a computational resource. I.e. we have

recovered our failed CpuA process by redistributing

a new CpuA process.

7 CONCLUSIONS

We have presented a new unique process algebra

and a simulator tool for analytic fault injection and

for estimating descriptive statistics of quantifiable

properties of reliability and resource requirements of

a distributed system with complex behaviour

hereunder complex fault-tolerance behaviour. The

process algebra and tool have successfully been

applied on a number of examples.

Perspectives. The focus of the method is on analysis

and design (before implementation) of new

dependent distributed systems and could contribute

to the emergence of more reliable distributed

systems with predictable resource requirements. The

method could also be used to model and optimise

existing dependable systems.

It is also possible that Gπ-calculus’ could be

applied in the ongoing attempts to apply process

algebras in describing the computational potential of

biological processes by accounting for the seemingly

unreliable computational environment of the living

cell.

Areas which apply cheap computational

resources on large scale where failure is frequent

could also potentially benefit from this method by

analysing fault-tolerance behaviour which could

compensate for the unreliability of the

computational resources.

Further Work. One way to introduce the Gπ-

calculus method to a wider audience which are not

acquainted with process algebras could be to

integrate Gπ-calculus with an existing accepted and

widely used method such as UML (Fowler, 2003). It

seems useful and trivial to extend the tools to present

the executions of Gπ-calculus expressions as

sequence diagrams since we just have to draw a

UML object box for a process group and then

present the Gπ-reactions between the components

(process groups) by drawing directed action arrows

between the time lines of the UML object boxes. If

we model UML components as process groups then

Gπ-calculus models could formalise the connection

between UML component diagrams and UML

sequence diagrams a formalisation which does not

exists today.

ACKNOWLEDGEMENTS

This work is partially funded by ARTIST2 (IST-

004527), MoDES (Danish Research Council 2106-

05-0022) and the Danish National Advanced

Technology Foundation under project DaNES.

REFERENCES

Amadio, Roberto M., 1997. An asynchronous model of

locality, failure, and process mobility. In D. Garlan

and D. LeM´etayer, editors, Proceedings of the 2nd

International Conference on Coordination Languages

and Models (COORDINATION’97), volume 1282,

pages 374–391, Berlin, Germany. Springer-Verlag.

Fowler, Martin, 2003. UML Distilled: A Brief Guide to the

Standard Object Modeling Language. 3rd Edition. The

Addison-Wesley Object Technology Series.

Francalanza, Adrian and Hennessy, Matthew, 2006. A

theory for observational fault-tolerance. Lecture

Notes in Computer Science (including subseries

Lecture Notes in Artificial Intelligence and Lecture

Notes in Bioinformatics). 3921 LNCS.

Milner, Robin, 1999. Communicating and Mobile

Systems: the Pi-Calculus, Cambridge Univ. Press.

Plotkin, G, 1981. A structural approach to operational

semantics. Tech. Rep. DAIMI FN-19, Computer

Science Dept., Aarhus University, Aarhus, Denmark.

Priami, Corrado, 1995. Stochastic pi-Calculus. Comput. J.

38(7): 578-589.

Sellberg, Christian, 2008. Model and Tool for Fault

Analysis in Distributed Systems. Master Thesis.

Informatics and Mathematical Modelling, Technical

University of Denmark, {DTU}.

Tanenbaum, Andrew S., Maarten van Steen, 2006.

Distributed Systems: Principles and Paradigms.

Prentice Hall; 2 edition.

ICSOFT 2008 - International Conference on Software and Data Technologies