IMPROVING QUALITY OF RULE SETS BY INCREASING

INCOMPLETENESS OF DATA SETS

A Rough Set Approach

Jerzy W. Grzymala-Busse

Department of Electrical Engineering and Computer Science, University of Kansas

1520 W. 15-th St., Lawrence, KS 66045, U.S.A.

Witold J. Grzymala-Busse

Touchnet Information Systems, Inc.,15520 College Blvd., Lenexa, KS 66219, U.S.A.

Keywords:

Rough set theory, rule induction, MLEM2 algorithm, missing attribute values, lost values, attribute-concept

values, ”do not care” conditions.

Abstract:

This paper presents a new methodology to improve the quality of rule sets. We performed a series of data

mining experiments on completely speciﬁed data sets. In these experiments we removed some speciﬁed at-

tribute values, or, in different words, replaced such speciﬁed values by symbols of missing attribute values,

and used these data for rule induction while original, complete data sets were used for testing. In our exper-

iments we used the MLEM2 rule induction algorithm of the LERS data mining system, based on rough sets.

Our approach to missing attribute values was based on rough set theory as well. Results of our experiments

show that for some data sets and some interpretation of missing attribute values, the error rate was smaller

than for the original, complete data sets. Thus, rule sets induced from some data sets may be improved by

increasing incompleteness of data sets. It appears that by removing some attribute values, the rule induction

system, forced to induce rules from remaining information, may induce better rule sets.

1 INTRODUCTION

Recently data mining experiments with data sets

affected by missing attribute values were reported

(Grzymala-Busse and Grzymala-Busse, 2007). In

these experiments we conducted a series of experi-

ments on data sets that were originally complete, i.e.,

all attribute values were speciﬁed. First, for each

data set, a portion of 10% of the total number of at-

tribute values was replaced by special symbols denot-

ing missing attribute values, or, in different words,

this portion was replaced by missing attribute values.

Then, with an increment of 10%, among remaining

speciﬁed attribute values, a new portion of 10% was

replaced by symbols of missing attribute values. This

process was continued, with an increment of 10%, un-

til all speciﬁed attribute values were replaced by sym-

bols of missing attribute values. Then, for all data

sets, error rates were computed using ten-fold cross

validation. Obviously, during ten-fold cross valida-

tion experiments both training data and testing data,

with the exception of original, complete data sets,

were incomplete. It was observed that for some data

sets an error rate was surprisingly stable, i.e., was not

increasing as expected with an increase of the percent-

age of missing attribute values.

Therefore we decided to perform additional but

different experiments of ten-fold cross validation in

which training data sets are taken from incomplete

data sets while testing data sets were taken from the

original, complete data sets.

In (Grzymala-Busse and Grzymala-Busse, 2007)

we discussed three types of missing attribute val-

ues: lost values (the values that were recorded but

currently are unavailable), attribute-concept values

(these missing attribute values may be replaced by

any attribute value limited to the same concept),

and”do not care” conditions (the original values were

irrelevant). A concept (class) is a set of all cases clas-

siﬁed (or diagnosed) the same way.

Two special data sets with missing attribute values

were extensively studied: in the ﬁrst case, all miss-

ing attribute values are lost, in the second case, all

missing attribute values are ”do not care” conditions.

Incomplete decision tables in which all attribute val-

ues are lost, from the viewpoint of rough set theory,

241

W. Grzymala-Busse J. and J. Grzymala-Busse W. (2008).

IMPROVING QUALITY OF RULE SETS BY INCREASING INCOMPLETENESS OF DATA SETS - A Rough Set Approach.

In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 241-248

DOI: 10.5220/0001881902410248

 SciTePress

were studied for the ﬁrst time in (Grzymala-Busse

and Wang, 1997), where two algorithms for rule in-

duction, modiﬁed to handle lost attribute values, were

presented. This approach was studied later, e.g., in

(Stefanowski and Tsoukias, 1999; Stefanowski and

Tsoukias, 2001), where the indiscernibility relation

was generalized to describe such incomplete decision

tables.

In attribute-concept values interpretation of a

missing attribute value, the missing attribute value

may be replaced by any value of the attribute domain

restricted to the concept to which the case with a miss-

ing attribute value belongs. For example, if for a pa-

tient the value of an attribute Temperature is missing,

this patient is sick with ﬂu, and all remaining patients

sick with ﬂu have values high or very high for Tem-

perature when using the interpretation of the miss-

ing attribute value as the attribute-concept value, we

will replace the missing attribute value with high and

very high. This approach was studied in (Grzymala-

Busse and Hu, 2000; Grzymala-Busse, 2004).

On the other hand, incomplete decision tables in

which all missing attribute values are ”do not care”

conditions, from the view point of rough set theory,

were studied for the ﬁrst time in (Grzymala-Busse,

1991), where a method for rule induction was in-

troduced in which each missing attribute value was

replaced by all values from the domain of the at-

tribute (Grzymala-Busse, 1991). Such incomplete

decision tables, with all missing attribute values be-

ing ”do not care conditions”, were broadly studied in

(Kryszkiewicz, 1995; Kryszkiewicz, 1999), including

extending the idea of the indiscernibility relation to

describe such incomplete decision tables.

In this paper we report results of different exper-

iments. In our new experiments, for every complete

data set, we created a series of incomplete data sets by

starting with a portion of 5% of the total number of at-

tribute values. Then this portion of missing attribute

values was incrementally enlarged, with an increment

equal to 5% of the total number of missing attribute

values.

Our new experiments started from creation, for

every complete data set, a basic series of incremen-

tally larger portions of missing attribute values with

all missing attribute values being equal to ”?” (lost

values). For every basic series of data sets with miss-

ing attribute values, new series of data sets with miss-

ing attribute values were obtained by replacing all

symbols of ”?” by symbols of ”−” and ”*”, denoting

different types of missing attribute values (attribute-

concept values and ”do not care” conditions). Addi-

tionally, the same basic series of data sets were used

to induce certain and possible rule sets.

Note that our basic assumption was that for every

case at least one attribute value should be speciﬁed.

Thus, the process of enlarging the portion of miss-

ing attribute values was terminated when, during three

different attempts to replace speciﬁed attribute values

by missing ones, a case with all missing attribute val-

ues was generated.

In general, incomplete decision tables are de-

scribed by characteristic relations, in a similar way as

complete decision tables are described by indiscerni-

bility relations (Grzymala-Busse, 2003).

In rough set theory, one of the basic notions is the

idea of lower and upper approximations. For com-

plete decision tables, once the indiscernibility relation

is ﬁxed and the concept (a set of cases) is given, the

lower and upper approximations are unique.

For incomplete decision tables, there are three im-

portant and different possibilities to deﬁne lower and

upper approximations, called singleton, subset, and

concept approximations (Grzymala-Busse, 2003).

Singleton lower and upper approximations were stud-

ied, e.g., in (Kryszkiewicz, 1995; Kryszkiewicz,

1999; Stefanowski and Tsoukias, 1999; Stefanowski

and Tsoukias, 2001). Note that similar deﬁnitions of

lower and upper approximations, though not for in-

complete decision tables, were studied in (Lin, 1992;

Slowinski and Vanderpooten, 2000; Yao, 1998). Fur-

ther deﬁnitions of approximations were discussed in

(Grzymala-Busse and Rzasa, 2006; Grzymala-Busse

and Rzasa, 2007). Additionally, note that some

other rough-set approaches to missing attribute values

were presented in (Grzymala-Busse, 1991; Grzymala-

Busse and Hu, 2000; Wang, 2002) as well.

2 LOWER AND UPPER

APPROXIMATIONS

We assume that the input data sets are presented in

the form of a decision table. Rows of the decision

table represent cases, while columns are labeled by

variables. The set of all cases will be denoted by U.

Independent variables are called attributes and a de-

pendent variable is called a decision and is denoted

by d. The set of all attributes will be denoted by A.

Any decision table deﬁnes a function ρ that maps the

direct product of U and A into the set of all values. A

decision table with an incompletely speciﬁed function

ρ will be called incomplete.

For the rest of the paper we will assume that all de-

cision values are speciﬁed, i.e., they are not missing.

Also, we will assume that lost values will be denoted

by ”?”, attribute-concept values by ”−”, and ”do not

care” conditions by ”*”. Additionally, we will assume

ICSOFT 2008 - International Conference on Software and Data Technologies

242

that for each case at least one attribute value is speci-

ﬁed.

For completely speciﬁed decision tables, let B de-

note a nonempty subset of the set A. An indiscerni-

bility relation R associated with B is deﬁned for all

x, y ∈ U by x R y if and only if for both x and y the

values for all variables from B are identical (Pawlak,

1982; Pawlak, 1991). An equivalence class of R con-

taining x is denoted [x]

. Any ﬁnite union of elemen-

tary sets of P is called a B-deﬁnable set. Let X be

any subset of the set U. The set X is called a concept

and is usually deﬁned as the set of all cases deﬁned

by a speciﬁc value of the decision. In general, X is

not a B-deﬁnable set. However, set X may be approx-

imated by two B-deﬁnable sets, the ﬁrst one is called

a B-lower approximation of X, denoted by BX and

deﬁned as follows

{x ∈ U | [x]

⊆ X}.

The second set is called a B-upper approximation of

X, denoted by BX and deﬁned as follows

{x ∈ U | [x]

∩ X 6=

0},

(Pawlak, 1982; Pawlak, 1991). The above shown

way of computing lower and upper approximations,

by constructing these approximations from singletons

x, will be called the ﬁrst method. The B-lower approx-

imation of X is the greatest B-deﬁnable set, contained

in X. The B-upper approximation of X is the smallest

B-deﬁnable set containing X.

As it was observed in (Pawlak, 1991), for com-

plete decision tables we may use a second method to

deﬁne the B-lower approximation of X, by the follow-

ing formula

∪{[x]

| x ∈ U, [x]

⊆ X},

and the B-upper approximation of x may be deﬁned,

using the second method, by

∪{[x]

| x ∈ U, [x]

∩ X 6=

0}.

Obviously, for complete decision tables both methods

result in the same respective sets, i.e., corresponding

lower approximations are identical, and so are upper

approximations.

Let a be an attribute, i.e., a ∈ A and let v be a

value of a for some case. For complete decision ta-

bles if t = (a, v) is an attribute-value pair then a block

of t, denoted [t], is a set of all cases from U that for

attribute a have value v. For incomplete decision ta-

bles the deﬁnition of a block of an attribute-value pair

must be modiﬁed in the following way:

• If for an attribute a there exists a case x such

that ρ(x, a) =?, i.e., the corresponding value is

lost, then the case x should not be included in any

blocks[(a, v)] for all values v of attribute a,

• If for an attribute a there exists a case x such that

the corresponding value is an attribute-concept

value, i.e., ρ(x, a) = −, then the corresponding

case x should be included in blocks [(a, v)] for all

speciﬁed values v ∈ V(x, a) of attribute a, where

V(x, a) = {ρ(y, a) | ρ(y, a) is speciﬁed,

y ∈ U, ρ(y, d) = ρ(x, d)}.

• If for an attribute a there exists a case x such that

the corresponding value is a ”do not care” condi-

tion, i.e., ρ(x, a) = ∗, then the case x should be

included in blocks [(a, v)] for all speciﬁed values

v of attribute a,

For a case x∈ U the characteristicset K

(x) is deﬁned

as the intersection of the sets K(x, a), for all a ∈ B,

where the set K(x, a) is deﬁned in the following way:

• If ρ(x, a) is speciﬁed, then K(x, a) is the block

[(a, ρ(x, a)] of attribute a and its value ρ(x, a),

• If ρ(x, a) =? or ρ(x, a) = ∗ then the set K(x, a) =

• If ρ(x, a) = −, then the corresponding set K(x, a)

is equal to the union of all blocks of attribute-

value pairs (a, v), where v ∈ V(x, a) if V(x, a) is

nonempty. If V(x, a) is empty, K(x, a) = U.

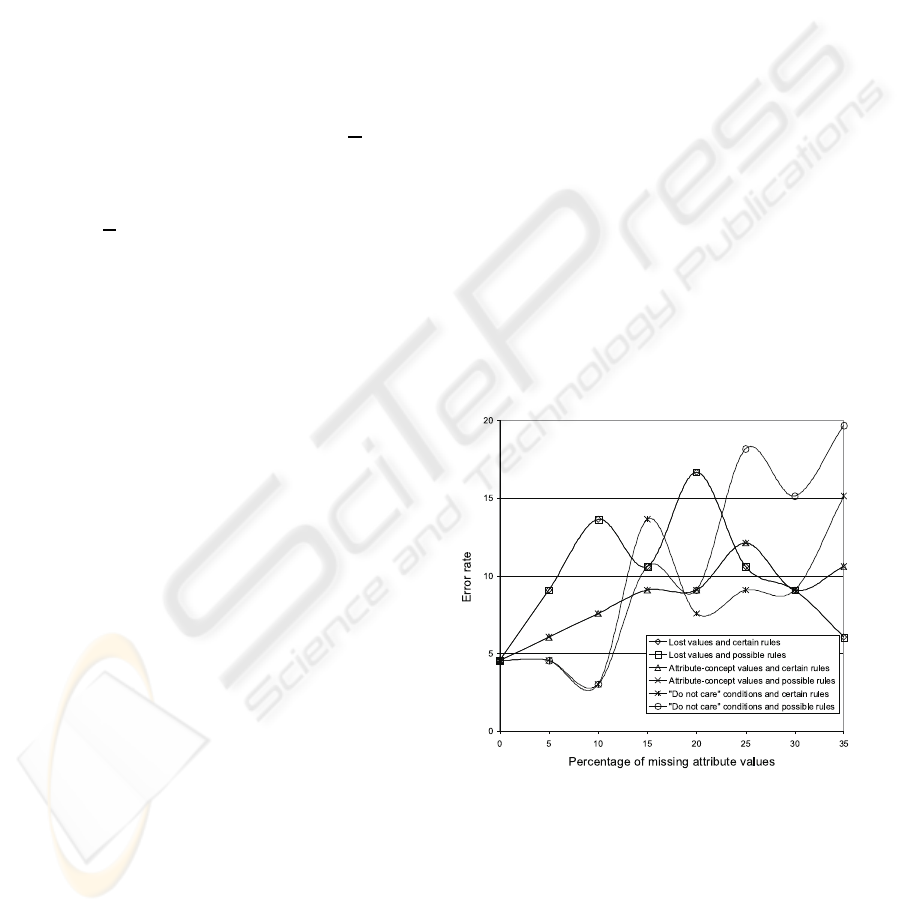
Figure 1: Bankruptcy data set.

For incomplete decision tables lower and upper

approximations may be deﬁned in a few different

ways. In this paper we suggest concept deﬁnitions

of lower and upper approximations for incomplete

decision tables, following (Grzymala-Busse, 2003).

Again, let X be a concept, let B be a subset of the

set A of all attributes, and let K

(x) be the charac-

teristic set of the incomplete decision table, where

IMPROVING QUALITY OF RULE SETS BY INCREASING INCOMPLETENESS OF DATA SETS - A Rough Set

Approach

243

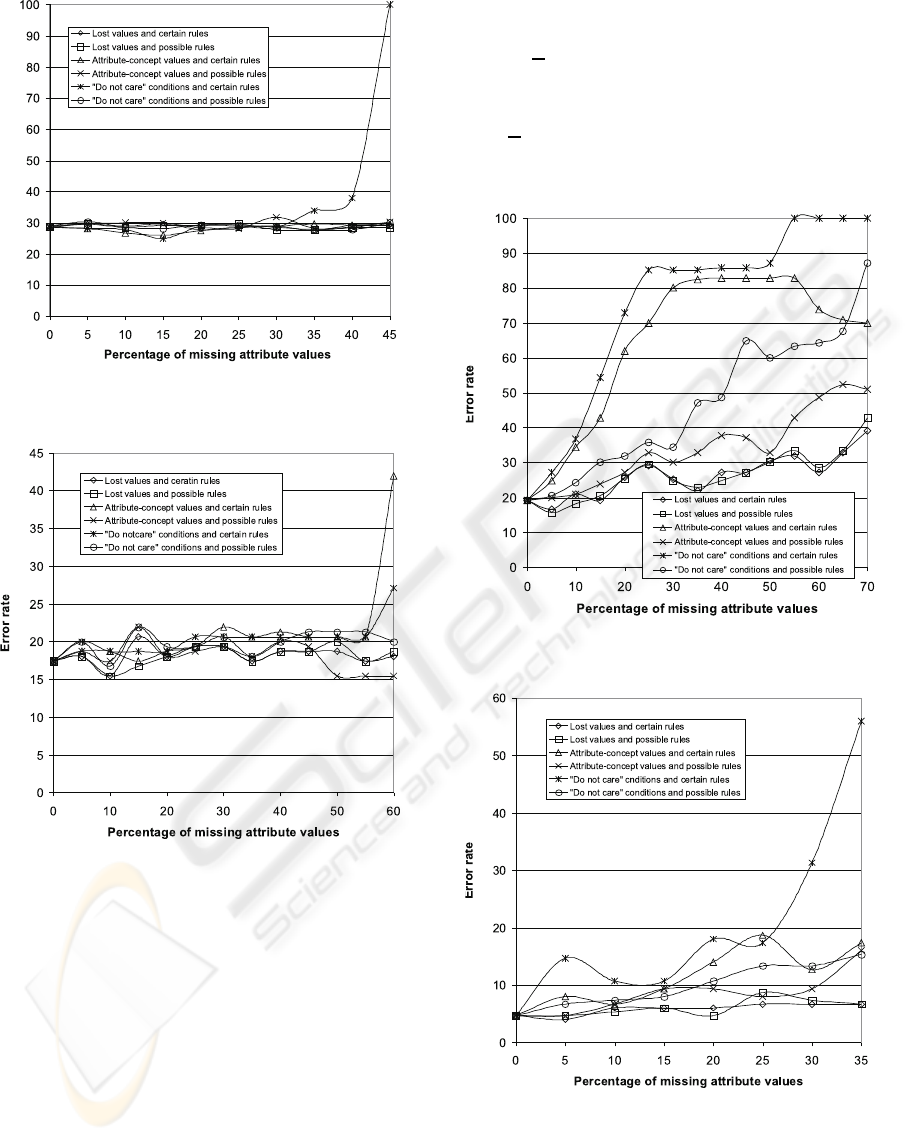
Figure 2: Breast cancer data set.

Figure 3: Hepatitis data set.

x ∈ U. The ﬁrst possibility is to use the ﬁrst Pawlak’s

method to deﬁne lower and upper approximations, us-

ing characteristic sets instead of equivalence classes

of the indiscernibility relation. This idea was dis-

cussed in (Kryszkiewicz, 1995; Kryszkiewicz, 1999;

Stefanowski and Tsoukias, 1999; Stefanowski and

Tsoukias, 2001). Such approximations are called sin-

gleton.

The second method of deﬁning lower and up-

per approximations for complete decision tables uses

another idea: lower and upper approximations are

unions of characteristic sets, i.e., we use the second

Pawlak’s method. Although there are two ways to do

this, we will quote only on of them. A concept B-

lower approximation of X is deﬁned as follows:

BX = ∪{K

(x) | x ∈ X, K

(x) ⊆ X}.

A concept B-upper approximation of the concept X is

deﬁned as follows:

BX = ∪{K

(x) | x ∈ X, K

(x) ∩ X 6=

0} =

= ∪{K

(x) | x ∈ X}.

Figure 4: Image segmentation data set.

Figure 5: Iris data set.

ICSOFT 2008 - International Conference on Software and Data Technologies

244

Figure 6: Lymphography data set.

Figure 7: Wine data set.

3 LERS AND LEM2

The data system LERS (Learning from Examples

based on Rough Sets) (Grzymala-Busse, 1997) in-

duces rules from incomplete data, i.e., data with miss-

ing attribute values, from data with numerical at-

tributes, and from inconsistent data, i.e., data with

conﬂicting cases. Two cases are conﬂicting when they

are characterized by the same values of all attributes,

but they belong to different concepts (classes). LERS

uses rough set theory to compute lower and upper ap-

proximations for concepts involved in conﬂicts with

other concepts.

Rules induced from the lower approximation of

Table 1: Data sets used for experiments.

Data set Number of

cases attributes concepts

Bankruptcy 66 5 2

Breast cancer 277 9 2

Hepatitis 155 19 2

Image segmentation 210 19 7

Iris 150 4 3

Lymphography 148 18 4

Wine 178 13 3

Table 2: Error rate for the breast cancer. data set.

Percentage of Rules

Lost values certain possible

0 28.52 28.88

5 29.6 29.6

10 28.88 28.52

15 29.6 29.24

20 27.8 29.24

25 28.52 29.6

30 28.88 27. 8

35 27.44 27.8

40 29.24 28.52

45 29.24 28.52

the concept certainly describe the concept, hence such

rules are called certain (Grzymala-Busse, 1988). On

the other hand, rules induced from the upper approx-

imation of the concept describe the concept possibly,

so these rules are called possible (Grzymala-Busse,

1988). For rule induction LERS uses three algo-

rithms: LEM1, LEM2, and MLEM2.

3.1 LEM2

The LEM2 algorithm of LERS is most frequently

used for rule induction since—in most cases—it gives

better results than LEM1. LEM2 explores the search

space of attribute-value pairs. Its input data set is a

lower or upper approximation of a concept, so its in-

put data set is always consistent. In general, LEM2

computes a local covering and then converts it into

a rule set. We will quote a few deﬁnitions to de-

scribe the LEM2 algorithm (Chan and Grzymala-

Busse, 1991; Grzymala-Busse, 2002).

The LEM2 algorithm is based on an idea of an

IMPROVING QUALITY OF RULE SETS BY INCREASING INCOMPLETENESS OF DATA SETS - A Rough Set

Approach

245

Table 3: Error rate for the hepatitis. data set.

Percentage of Rules

Lost values certain possible

0 17.42 17.42

5 18.06 18.06

10 15.48 15.48

15 20.65 16.77

20 18.06 18.06

25 19.35 19.35

30 19.35 19.35

35 17.42 17.42

40 18.71 18.71

45 18.71 18.71

50 18.71 20.0

55 17.42 17.42

60 18.06 18.71

attribute-value pair block. Let X be a nonempty lower

or upper approximation of a concept represented by a

decision-value pair (d, w). Set X depends on a set T

of attribute-value pairs t = (a, v) if and only if

0 6= [T] =

t∈T

[t] ⊆ X.

Set T is a minimal complex of X if and only if

X depends on T and no proper subset T

′

of T exists

such that X depends on T

′

. Let T be a nonempty

collection of nonempty sets of attribute-value pairs.

Then T is a local covering of X if and only if the

following conditions are satisﬁed:

• each member T of T is a minimal complex of X,

•

t∈T

[T] = X, and

• T is minimal, i.e., T has the smallest possible

number of members.

MLEM2, a modiﬁed version of LEM2, processes

numerical attributes differently than symbolic at-

tributes. For numerical attributes MLEM2 sorts all

values of a numerical attribute. Then it computes cut-

points as averages for any two consecutive values of

the sorted list. For each cutpoint q MLEM2 creates

two blocks, the ﬁrst block contains all cases for which

values of the numerical attribute are smaller than q,

the second block contains remaining cases, i.e., all

cases for which values of the numerical attribute are

larger than q. The search space of MLEM2 is the

set of all blocks computed this way, together with

blocks deﬁned by symbolic attributes. Starting from

Table 4: Error rate for the iris. data set.

Percentage of Rules

Lost values certain possible

0 4.67 4.67

5 4.0 4.67

10 6.0 5.33

15 6.0 6.0

20 6.0 4.67

25 6.67 7.33

30 6.67 7.33

35 6.67 6.67

that point, rule induction in MLEM2 is conducted the

same way as in LEM2.

3.2 LERS Classiﬁcation System

Rule sets, induced from data sets, are used mostly to

classify new, unseen cases. A classiﬁcation system

used in LERS is a modiﬁcation of the well-known

bucket brigade algorithm (Booker et al., 1990; Hol-

land et al., 1986).

The decision to which concept a case belongs to

is made on the basis of three factors: strength, speci-

ﬁcity, and support. These factors are deﬁned as foll:

strength is the total number of cases correctly classi-

ﬁed by the rule during training. Speciﬁcity is the total

number of attribute-value pairs on the left-hand side

of the rule. The matching rules with a larger num-

ber of attribute-value pairs are considered more spe-

ciﬁc. The third factor, support, is deﬁned as the sum

of products of strength and speciﬁcity for all match-

ing rules indicating the same concept. The concept C

for which the support, i.e., the following expression

∑

matching rules r describing C

Strength(r) ∗ Speciﬁcity(r)

is the largest is the winner and the case is classiﬁed as

being a member of C.

In the classiﬁcation system of LERS, if complete

matching is impossible, partial matching is applied,

for details see (Grzymala-Busse, 1997).

4 EXPERIMENTS

In our experiments we used seven typical data sets,

see Table 1. All of these data sets are available from

the UCI ML Repository, with the exception of the

bankruptcy data set.

ICSOFT 2008 - International Conference on Software and Data Technologies

246

Table 5: Error rate for the lymphography. data set.

Percentage of Rules

Lost values certain possible

0 18.92 18.92

5 14.19 14.19

10 18.92 18.92

15 18.92 18.92

20 21.62 21.62

25 18.92 17.57

30 17.57 16.22

35 20.27 20.95

40 22.30 22.3

45 21.62 21.62

50 22.30 22.30

55 19.59 19.59

60 21.62 22.97

During experiments of ten-fold cross validation,

training data sets were affected by an incrementally

larger portion of missing attribute values, while test-

ing data sets were always the original, complete data

sets.

The MLEM2 algorithm was used for rule induc-

tion, while concept lower and upper approximations

were used for rule induction of certain and possible

rules, respectively.

For any ten experiments of ten-fold cross valida-

tion all ten parts for both data sets: complete and in-

complete were pairwise equal (if not taking missing

attribute values into account), i.e., any such two parts,

complete and incomplete, would be equal if we will

put back the appropriate speciﬁed attribute values into

the incomplete part.

Results of experiments are presented in Figures 1-

7. For some data sets (bankruptcy and image) the er-

ror rate increases rather consistently with our expec-

tations: with an increase in the percentage of missing

attribute values, the error rate increases as well. On

the other hand, it is quite clear that for some data sets

(breast, hepatitis, iris, lymphography and wine) the

error rate is approximately stable with an increase of

the percentage of missing attribute values of the type

lost, while for some data sets (breast and hepatitis)

the error rate is stable for all three types of missing

attribute values, except the largest percentage of miss-

ing attribute values. Note also that there is not a big

difference between certain and possible rule sets with

the exception of certain rule sets and ”do not care”

conditions, where the error rate is large due to empty

Table 6: Error rate for the wine. data set.

Percentage of Rules

Lost values certain possible

0 6.18 6.18

5 5.06 4.49

10 10.67 8.99

15 8.99 6.74

20 7.87 7.87

25 6.74 6.18

30 7.30 7.30

35 6.18 5.62

40 5.62 6.74

45 8.99 7.30

50 7.87 7.30

55 9.55 8.99

60 8.43 7.30

65 7.87 10.11

lower approximations for a large percentage of the

”do not care” conditions.

Additionally, exact error rates are presented for

ﬁve data sets: (breast, hepatitis, iris, lymphography

and wine) for missing attribute values of the type lost.

Most surprisingly, from Tables 2-6 it is clear that for

some percentage of lost values the error rate is smaller

than for complete data sets (0% of lost values).

5 CONCLUSIONS

As follows from our experiments, rule sets induced

from some data sets may be improved by replacing

speciﬁed attribute values by missing attribute values

of the type lost. Thus, in the process of data mining it

makes sense to try to replace some portion of attribute

values by missing attribute values of the type lost and

check whether the error rate decreases. Replacing a

portion of attribute values by missing attribute val-

ues of the type lost corresponds to hiding from the

rule induction system some information. It appears

that for some data sets the rule induction system, re-

turning new rule sets, occasionally ﬁnds better regu-

larities, hidden in the remaining information. Addi-

tionally, the fact that the error rate does not increase

with replacementof larger and larger portions of spec-

iﬁed attribute values by missing ones testiﬁes that the

rough-set approach to missing attribute values is very

good.

IMPROVING QUALITY OF RULE SETS BY INCREASING INCOMPLETENESS OF DATA SETS - A Rough Set

Approach

247

REFERENCES

Booker, L. B., Goldberg, D. E., and F., H. J. (1990). Clas-

siﬁer systems and genetic algorithms. In Carbonell,

J. G., editor, Machine Learning. Paradigms and Meth-

ods, pages 235–282. MIT Press, Boston.

Chan, C. C. and Grzymala-Busse, J. W. (1991). On the

attribute redundancy and the learning programs ID3,

PRISM, and LEM2. Technical report, Department of

Computer Science, University of Kansas.

Grzymala-Busse, J. W. (1988). Knowledge acquisition un-

der uncertainty—A rough set approach. Journal of

Intelligent & Robotic Systems, 1:3–16.

Grzymala-Busse, J. W. (1991). On the unknown attribute

values in learning from examples. In Proceedings

of the ISMIS-91, 6th International Symposium on

Methodologies for Intelligent Systems, pages 368–

377.

Grzymala-Busse, J. W. (1997). A new version of the rule

induction system LERS. Fundamenta Informaticae,

31:27–39.

Grzymala-Busse, J. W. (2002). MLEM2: A new algorithm

for rule induction from imperfect data. In Proceed-

ings of the 9th International Conference on Informa-

tion Processing and Management of Uncertainty in

Knowledge-Based Systems, (IPMU 2002), pages 243–

250.

Grzymala-Busse, J. W. (2003). Rough set strategies to data

with missing attribute values. In Workshop Notes,

Foundations and New Directions of Data Mining, in

conjunction with the 3-rd International Conference on

Data Mining, pages 56–63.

Grzymala-Busse, J. W. (2004). Three approaches to miss-

ing attribute values—a rough set perspective. In Pro-

ceedings of the Workshop on Foundation of Data Min-

ing, in conjunction with the Fourth IEEE International

Conference on Data Mining, pages 55–62.

Grzymala-Busse, J. W. and Grzymala-Busse, W. J. (2007).

An experimental comparison of three rough set ap-

proaches to missing attribute values. In Peters, J. F.

and Skowron, A., editors, Transactions on Rough Sets,

pages 31–50. Springer-Verlag, Berlin, Heidelberg.

Grzymala-Busse, J. W. and Hu, M. (2000). A comparison

of several approaches to missing attribute values in

data mining. In Proceedings of the Second Interna-

tional Conference on Rough Sets and Current Trends

in Computing, pages 340–347.

Grzymala-Busse, J. W. and Rzasa, W. (2006). Local and

global approximations for incomplete data. In Pro-

ceedings of the RSCTC 2006, the Fifth International

Conference on Rough Sets and Current Trends in

Computing, pages 244–253.

Grzymala-Busse, J. W. and Rzasa, W. (2007). Deﬁnabil-

ity of approximations for a generalization of the indis-

cernibility relation. In Proceedings of the 2007 IEEE

Symposium on Foundations of Computational Intelli-

gence (IEEE FOCI 2007), pages 65–72.

Grzymala-Busse, J. W. and Wang, A. Y. (1997). Modiﬁed

algorithms LEM1 and LEM2 for rule induction from

data with missing attribute values. In Proceedings of

the Fifth International Workshop on Rough Sets and

Soft Computing (RSSC’97) at the Third Joint Confer-

ence on Information Sciences (JCIS’97), pages 69–72.

Holland, J. H., Holyoak, K. J., and Nisbett, R. E. (1986).

Induction. Processes of Inference, Learning, and Dis-

covery. MIT Press, Boston.

Kryszkiewicz, M. (1995). Rough set approach to incom-

plete information systems. In Proceedings of the

Second Annual Joint Conference on Information Sci-

ences, pages 194–197.

Kryszkiewicz, M. (1999). Rules in incomplete information

systems. Information Sciences, 113:271–292.

Lin, T. Y. (1992). Topological and fuzzy rough sets. In

Slowinski, R., editor, Intelligent Decision Support.

Handbook of Applications and Advances of the Rough

Sets Theory, pages 287–304. Kluwer Academic Pub-

lishers, Dordrecht, Boston, London.

Pawlak, Z. (1982). Rough sets. International Journal of

Computer and Information Sciences, 11:341–356.

Pawlak, Z. (1991). Rough Sets. Theoretical Aspects of Rea-

soning about Data. Kluwer Academic Publishers,

Dordrecht, Boston, London.

Slowinski, R. and Vanderpooten, D. (2000). A generalized

deﬁnition of rough approximations based on similar-

ity. IEEE Transactions on Knowledge and Data Engi-

neering, 12:331–336.

Stefanowski, J. and Tsoukias, A. (1999). On the exten-

sion of rough sets under incomplete information. In

Proceedings of the RSFDGrC’1999, 7th International

Workshop on New Directions in Rough Sets, Data

Mining, and Granular-Soft Computing, pages 73–81.

Stefanowski, J. and Tsoukias, A. (2001). Incomplete infor-

mation tables and rough classiﬁcation. Computational

Intelligence, 17:545–566.

Wang, G. (2002). Extension of rough set under in-

complete information systems. In Proceedings of

the IEEE International Conference on Fuzzy Systems

(FUZZ IEEE’2002), pages 1098–1103.

Yao, Y. Y. (1998). Relational interpretations of neighbor-

hood operators and rough set approximation opera-

tors. Information Sciences, 111:239–259.

ICSOFT 2008 - International Conference on Software and Data Technologies

248