EVALUATING SCHEDULES OF

ITERATIVE/INCREMENTAL SOFTWARE PROJECTS

FROM A REAL OPTIONS PERSPECTIVE

Vassilis C. Gerogiannis

, Androklis Mavridis

, Pandelis G. Ipsilandis

and Ioannis Stamelos

Department of Project Management, Technological Education Institute of Larissa, Greece

Department of Computer Science, Aristotle University of Thessaloniki, Greece

Keywords: Iterative/Incremental Software Projects, Real Options Analysis, Timeboxing.

Abstract: In an iterative/incremental software project, software is built in a sequence of iterations with each of them

providing certain parts of the required functionality. To better manage an incremental delivery plan,

iterations are usually performed during pre-specified time boxes. In a previous work, we addressed the

problem of optimizing the schedule of incremental software projects which follow an iterative, timeboxing

process model (TB projects). We approached scheduling as a multi criteria decision problem that can be

formulated by a linear programming model aimed to overcome some “rigid” simplifications of conventional

timeboxing, where durations of time boxes and stages are equal and a priori fixed. In this paper, we move

this decision making process one step forward by applying real options theory to analyze the investment

risks associated with each alternative scheduling decision. We identify two options in a TB project. The first

is to stall (abandon) the development at a pre-defined iteration, while the second is to continue (expand)

development and deliver the full functionality. Thus, we provide the manager the flexibility to decide the

most profitable (valued) combination of delivered functionalities, at a certain iteration, under favourable or

unfavourable conditions.

1 INTRODUCTION

A common management approach in iterative/

incremental software development projects is

timeboxing, i.e., to perform iterations during pre-

specified time periods, so called time boxes

(Stapleton, 2003). Timeboxing emphasizes on

improving the predictability of software delivery

times and avoiding, as much as possible, risks of

missing project deadlines, as these are determined

by the iteration time boxes (Jalote et al., 2004). A

timeboxed iteration delivers a working software

system that is generally an increment to the previous

delivery. Thus, the manager of a software project

which employs timeboxing (TB project) faces the

problem to specify the functionality to be delivered

within the context of each time box. By following a

“mini” waterfall approach, development work is

divided into a sequence of stages (e.g., requirements,

design, implementation, testing and deployment)

that are repeated iteratively and executed by small

dedicated development teams. Iterations in a TB

project can be rolled out in parallel to further

improve the project performance and reduce the

overall project duration. Parallelism is achieved by

following a “pipelined” execution that is similar to

instructions execution from hardware architectures.

When a team completes the tasks of a stage, it hands

over the intermediate deliverables to another team

executing the next stage and then starts executing

the same stage in the next timeboxed iteration.

In previous work we have defined a multi objective

linear programming (LP) model for scheduling TB

projects (Gerogiannis and Ipsilandis, 2007). We

have proposed a model that overcomes some

limitations of conventional timeboxing, where

timeboxes are ad hoc fixed, precedence constraints

between stages are simple sequential relationships

and possible work discontinuities due to

coordination overheads between stages in successive

iterations are not considered. This LP model

supports the software project manager to consider a

list of objectives regarding the overall project

performance (e.g., to minimize project duration,

iteration delays and work discontinuities).

Sensitivity analysis can provide some useful

224

C. Gerogiannis V., Mavridis A., G. Ipsilandis P. and Stamelos I. (2008).

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS PERSPECTIVE.

In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 224-233

DOI: 10.5220/0001894502240233

 SciTePress

information regarding cost trade-offs between these

scheduling decisions. The final outcome is a set of

alternative schedules (a portfolio of schedules), each

one characterized by a corresponding ratio between

iteration delay and work discontinuity costs.

In this paper, we build on this previous research

work and we apply a Real Options approach to

further enhance the overall decision making process

in TB projects. Real Options is a financial/decision

theory which addresses uncertainties inherent in

project investments over time and facilitates

adaptation of project management decisions to

dynamic environments (Myers, 1977). The

possibility to consider Real Options analysis is

particularly suitable in case of

software projects

(

Sullivan et al., 1999; Tiwana et al., 2006), when the

project manager has the opportunity (but not the

obligation) to make decisions in response to external or

internal events (e.g., defer the development, expand the

system functionalities, abandon the project etc.).

In order to present our approach, we describe the

scenario of an R&D department of a software

company that undertakes a software project in an

iterative/incremental, timeboxing development

fashion. We assume that the selection of the

appropriate schedule is a decision process that

involves the R&D management and the company’s

management board. The R&D management team

employs the LP model and identifies a set of

candidate schedules. These are then passed to the

managers of the board where they perform Net

Present Value (NPV) calculations to identify the

profitability of each alternative schedule. By

performing Real Options analysis, we will show

how the management board is benefited, in contrast

to the NPV approach, to undertake the proper project

scheduling decision that addresses potential

investment risks and uncertainties. Real Options

analysis can be applied to examine, at a certain

iteration, the value of the delivered functionalities.

Thus, the management board has the flexibility to

decide the most profitable (valued) combination of

functionalities, under favourable or unfavourable

conditions.

The paper is structured as follows: In section 2, we

briefly present the results conducted in our previous

work. In Section 3, we present an overview of Real

Options applicability in software project

management. In Section 4, we define the real

options to be analyzed in an iterative/incremental

project example. In section 5, we employ a set of

schedules for the example project and we apply a

Real Options approach in order to demonstrate how

the selection process of the most suitable schedule

can be supported. In the last section, we present

conclusions and directions of future research.

2 PREVIOUS WORK

In previous work we approached the problem of

finding optimum schedules for a TB project, from

the perspective of multi criteria decision analysis,

and we proposed alternative project schedules and

cost trade-offs as tools to be employed in order to

arrive at a suitable project scheduling decision

(Gerogiannis and Ipsilandis, 2007). A TB project

manager is assisted in selecting among alternative

schedules according to the relative magnitude of

each scheduling cost element (iteration delay costs

vs. work discontinuity costs). Thus, our approach

differs from other decision analysis methods applied

to release planning of iterative projects, since they

focus mainly on providing support for the selection

and prioritization of software requirements (Greer

and Ruhe, 2004; Akker et al., 2008).

In any TB project, we can identify that there is a set

of M stages and P project dependency relationships

(with or without time-lag). The project is divided

into N separate iterations in a “linear” way, where,

without loss of generality, the following assumptions

(originated from the timeboxing process model)

hold:

all stages are performed in all iterations,

a stage cannot be performed before the same stage is

completed in the previous iteration,

precedence dependencies remain the same in all

iterations (i.e., the same planning method is

followed).

By adopting an AON (Activities on Nodes) network

representation for the project life cycle, stages are

represented as nodes and dependency relationships

among stages are represented as arcs in the project

network. Precedence dependencies can be of any

type of the known relationships (Start-to-Start/SS,

Finish-to-Start/FS, Start-to-Finish/SF, Finish-to-

Finish / FF).

Let i = 1, 2, …, M denote the project stages and j =

1, 2, …, N denote the project iterations. Scheduling

of a TB project can be defined by a linear

programming (LP) model as follows.

I. Model Variables and Parameters. Define:

, the duration of stage i in iteration j,

, f

, the start and finish time respectively of stage i

in iteration j,

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS

PERSPECTIVE

225

, the minimum elapsed time for starting stage i

in iteration j+1 after finishing stage i in iteration j,

, the set of predecessor stages to stage i,

E , the set of all stages without successors,

, the total time of work breaks for stage i

because of work discontinuities in successive

iterations,

, the completion time of iteration j,

, the promised delivery/release time for the

software part produced in iteration j,

, the cost (per time unit) of delay in finishing

iteration j after the deadline,

, the cost (per time unit) of work breaks /

discontinuities in stage i.

II. Constraint definitions. Define:

Stage duration constraints:

= s

+ d

∀ i = 1, 2, …, M, j = 1, 2, …, N

Project linearity constraints:

ij+1

≥ f

+ l

∀ i = 1, 2, …, M, j=1, 2, …, N-1

Technological dependencies:

≥ f

∀ i = 1, 2,…, M, j = 1, 2, …, N, k ∈ P

Iteration completion time:

≥ f

∀ j = 1,2, …, N, k ∈ E

is the completion time for iteration j and UC

the project duration.

Resource delays (work breaks / discontinuities):

)

N-1

ij+1 ij

j=1

= (s f , i = 1,...,M

−∀

∑

i=1

=WB

∑

III. Global Objective Function. Depending on the

values of the cost parameters c

and f

, the following

general objective function:

Minimize

.( ) .

jj ii

j=1 i=1

cUC D fWB−+

∑∑

can be used to achieve different objectives or

analyze trade-offs between the cost parameters.

Examples include: i) minimize the project duration

(set c

equal to 1, rest of c

and f

equal to 0), ii)

minimize the total work break / discontinuity time

(set all f

equal to 1 and all c

equal to 0), iii)

minimize the completion time of iterations (set all f

equal to 0 and all c

equal to 1), iv) minimize the

total cost of work breaks / discontinuities (set all c

equal to 0), and v) minimize delay costs (set all f

equal to 0).

Sensitivity analysis on the parameters of this

objective function can be used to establish optimum

schedules at different levels of cost relations by

considering the ratio of iteration delay costs to the

costs of work breaks.

3 REAL OPTIONS IN SOFTWARE

PROJECTS

It is a common belief that the value for a given

software product is directly affected by its

development cost. However, research that has been

conducted since the mid of 90s, oriented towards the

employment of financial theories in software

engineering application areas, has highlighted the

needs for separating the value of a software product

from its cost, maximizing the value added by a given

software project investment as well as valuing the

hidden intangibles behind software development. An

example of such research initiatives are the

Economic Driven Software Engineering annual

workshops (EDSER, 2006).

Within this research context, there are efforts

towards the exploitation of the prominent economic

theory of Real Options (Myers, 1977) in order to

analyze, in a monetary fashion, the economic value

that different software investments could generate

(Amram and Kulatilaka, 1999; Benaroch, 2002). The

problem can be stated as follows: what is the most

appropriate option (from a portfolio of options) that

can result in the best value of a software product,

process or project? Hence, the problem of software

valuation can be viewed as a decision making

process that takes place under uncertainty and

incomplete knowledge. These uncertainties include

the cost and schedule required to develop a software

product, the software requirements which are likely

to change in the future, the presence of software

faults and failures, the impact of process/technology

changes on cost and scheduling elements, etc.

(Sullivan et al., 1999). The core idea is to cope with

these exogenous and endogenous uncertainties and

mitigate the corresponding risks in the project

investment. Such prediction is necessary for valuing

the long-term investment of adopting a particular

software development life cycle.

Classical financial techniques, such as

Discounted Cash Flow (DCF) and Net Present Value

(NPV) analysis, fall short in dealing with flexibility

and uncertainty in decision making (Schwartz and

Trigeorgis, 2000). The main problem with these

techniques is that they are best valid when valuing

ICSOFT 2008 - International Conference on Software and Data Technologies

226

an ongoing business or an immediate investment.

Real options theory (Myers, 1977) was developed to

address the inability of these conventional budgeting

techniques to address the strategic value of a project

investment. A real option gives the “option holder”

(e.g., the software project manager) the right, but not

the obligation, to evolve the software system and

enhance the project opportunities by making follow-

up investments (e.g., consider cases of reuse, expand

the range of provided functionalities, follow-up or

terminate the project, explore new markets etc.). If

conditions favourable to investing arise, the project

manager can exercise the option by investing the

strike price defined by the option. Therefore, real

options have been found a suitable approach to

introduce flexibility, facilitate active software

project management, and, consequently, handle the

dynamic nature and uncertainty of a given software

project investment (Wu et al., 2007).

The approach of planning an iterative TB

software project by taking into account multiple

factors (like iteration completion times, project

duration and work discontinuities for teams) and

trade-offs between them, offers the TB project

manager with the flexibility to consider a set of

optimum schedules. However, when selecting an

appropriate schedule for a project, based only on the

cost trade-offs and the project static expected value

(NPV), the TB project manager fails to consider

future uncertainties and, hence, to tally for project

risks. These uncertainties may range from internal

ones, such as an unexpected delay of a specific stage

in a certain iteration, to external ones, such as the

introduction to the market of a new development

tool/ technique that can ease the workload or

minimize cost. Counting the unexpected, the

software project manager has to be flexible.

Entering the Real Options realm, by utilizing the

LP model, presented in the previous section, we can

offer a portfolio of alternative scheduling options for

the TB project manager to choose. Each scheduling

option has a different inherent value (an option

value) which is the value of the produced software,

if this schedule is to be adopted. The manager has

the right to exercise this option and he/she can do so,

if certain business conditions become favourable for

the project success.

4 MAKING VALUE OUT OF A TB

SOFTWARE PROJECT

We will discuss the proposed approach through a

hypothetical scenario of a software company’s R&D

department. Timeboxing is a suitable process model

for developing projects which present a strong need

to deliver a working system quickly as well as for

projects of medium complexity which have a stable

architecture (Jalote et al., 2004). We assume that the

company’s R&D department executes this type of

projects in a timeboxing fashion. Before a project

commences, the R&D management utilizes the LP

model presented in section 2, identifies a set of

alternative schedules and justifies them since, under

certain conditions, a different schedule can be the

most suitable (in terms of project duration, iteration /

work discontinuity delays, cost elements, delivered

functionalities etc.).

After the schedules identification, the company’s

management board will be responsible to estimate

the best schedule profitability. When the most

profitable of the schedules is selected, the

development work in this iterative TB project will

begin. One possible solution is to calculate statically

the NPV for all candidate schedules, based on the

estimated project development costs (including

delay costs) and the expected free cash flows.

However, a combined Real Options–NPV approach

can provide a better way to deal with project

uncertainties and “discover” the “hidden value”

within all possible schedules. The management

board builds a step wise scenario, for each candidate

schedule, that involves a review of the incremental

delivery plan, to examine the delivered functionality

(i.e., the number of requirements developed) at a

certain point of the development life-cycle (i.e., at a

certain iteration) when a working pilot application is

planned to be available.

In the following, to simplify discussion, we make

the assumption that in the presented example all

necessary preparatory tasks (i.e., before identifying

and analyzing the real options to be investigated)

have been already performed, prior to the presented

analysis. These steps typically include, but are not

limited, to

(Sullivan et al., 1999; Tiwana et al.,

2006):

identify the real assets of a software project to be

analysed by real options (e.g. development costs and

future cash flows), monitor the important project

uncertainties and approximate the probability

distribution of these uncertainties.

We consider an example TB project life cycle that

follows a set of 6 stages which are executed in an

iterative/incremental approach. These stages are

Domain Modeling (stage A), Use-Cases Analysis

(stage B), Requirements Review (stage C),

Preliminary Design & Review (stage D), Detailed

Design & Review (stage E) and Coding & Testing

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS

PERSPECTIVE

227

(stage F). The work of each stage is done by a small

stage-specific team (2-3 experts) and all iterations

should be timeboxed. The final software application

is originally scheduled, according to the incremental

delivery plan, to be delivered after 6 iterations of

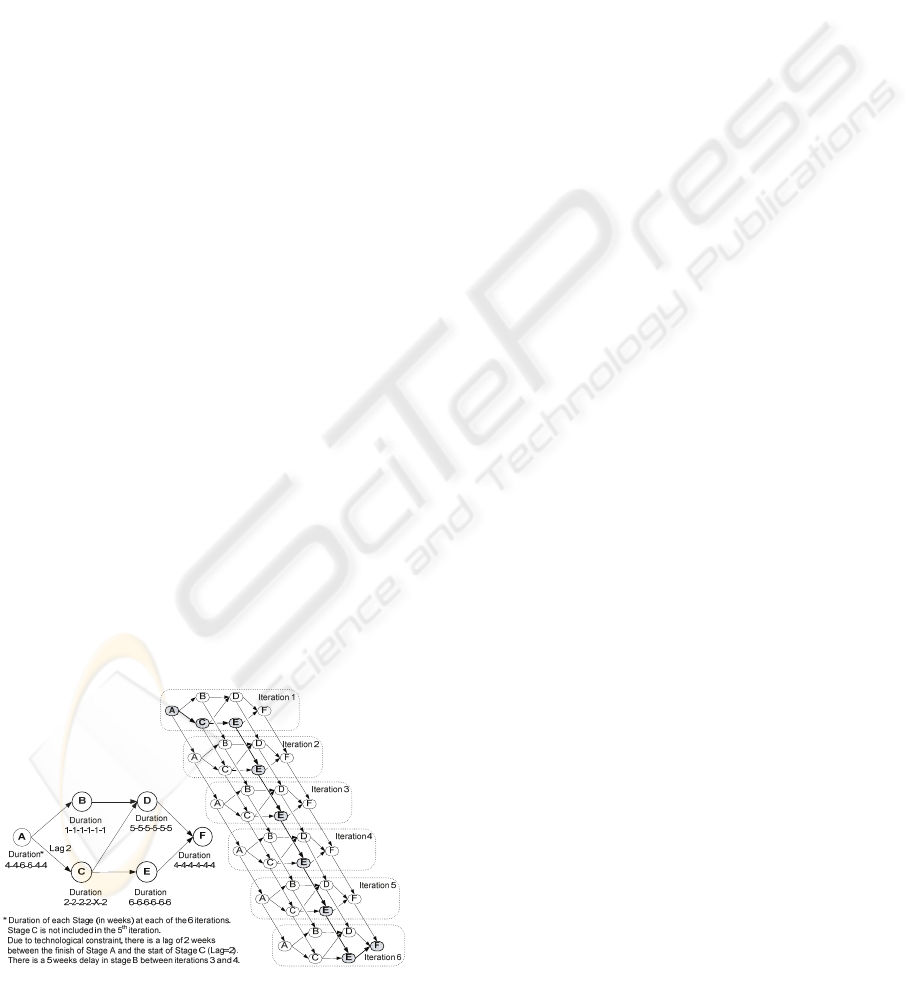
these 6 discrete stages. The AON diagram in Figure

1 depicts all stage relationships (they are FS

relationships) along with the most likely estimate (in

weeks) of the duration of each stage, at each of the 6

iterations. The critical path of the entire project

consists of stages A and C in iteration 1, the

sequence of stage E in all iterations, and stage F in

iteration 6.

We also consider that in this case project an

intermediate review will take place before the

beginning of the third iteration. If the delivered

functionality at that point is the promised and the

conditions (external: market competency, economic

situation etc. / internal: company status, company

policy, product uncertainty, resources uncertainty

etc.) are favourable, then the management board

decides to continue with the development of the rest

of the iterations. Otherwise, the board decides to

stall development and seek for salvage portion of the

costs. The first option (to stall development) is the

Option to Abandon, while the second (to proceed

with the full product development) is the Option to

Expand (Wu et al., 2007).

The application of such approach within the context

of an incremental/iterative life cycle might support

the successful development of a pilot software

application in a tight schedule. The management

board conceives the first batch of iterations as a pilot

application for the whole project. If the pilot

application meets the company’s

standards/customer’s expectations and the

conditions for its full development are favourable,

the company continues funding and proceeds to the

full scale/full functionality product.

Figure 1: Project AON network.

5 ANALYZING THE CASE

STUDY

In this section, we present the application of our

approach to the fictitious project discussed in the

previous section. Having defined the project life

cycle network structure (Figure 1), the project

duration (48 weeks) as well as the number of

iterations/increments (6), the development work is

constrained by a strict time plan of 1 year (48

working weeks) and a fixed budget (initial outlay) of

30,000€. The R&D management will suggest the

management board to evaluate three candidate

schedules, in terms of their profitability: i)

scheduling stages according to their Earliest Start

(Finish) time, ii) scheduling stages according to their

Latest Start time, and iii) scheduling stages to

minimize work discontinuities without extending the

overall project duration (48 weeks).

5.1 Alternative Schedules

As a first step, the R&D management, by setting in

the global objective function presented in section 2

set all f

equal to 0 and all c

equal to 1, obtains the

schedule that minimizes both the project duration

and the completion time (i.e., the release time for

software parts) of all iterations. This is actually the

schedule produced by the Critical Path Earliest Start

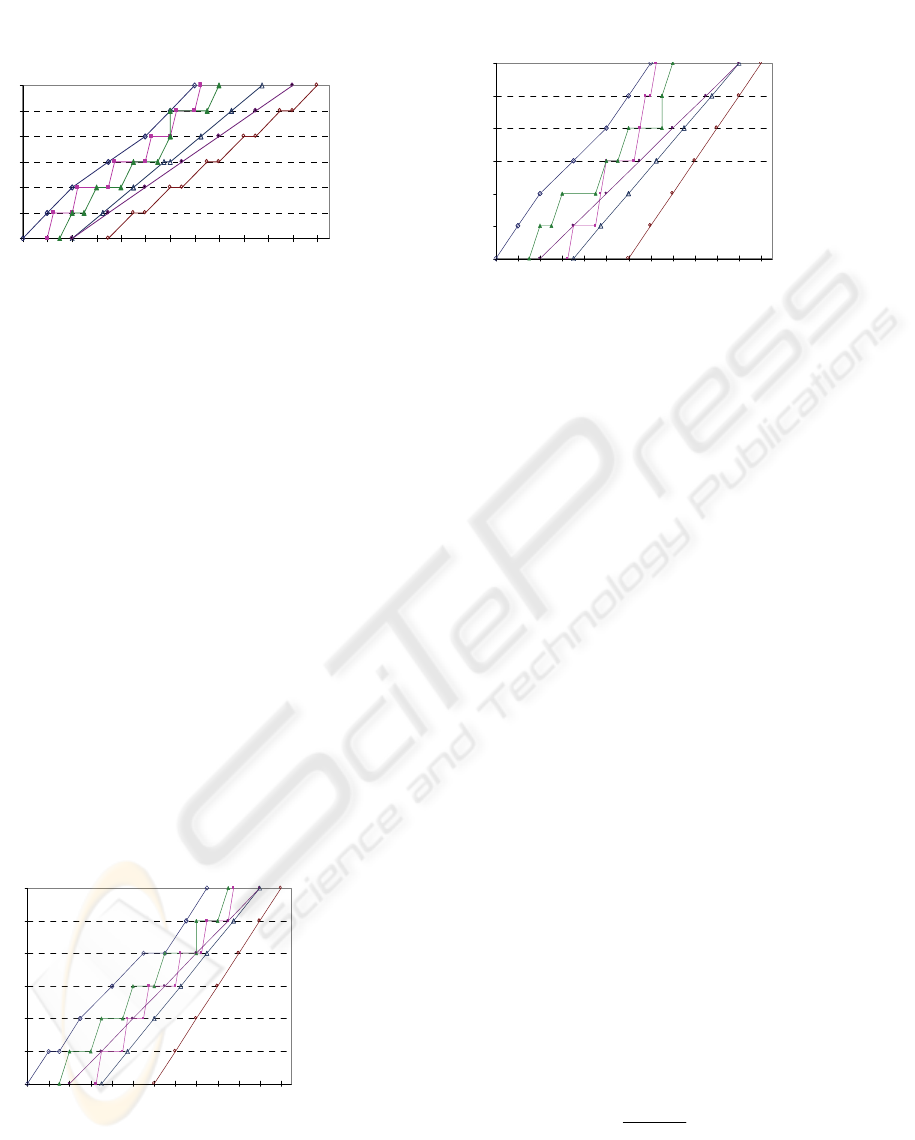
(Finish) Method (CPM EFT). Figure 2 presents a

linear scheduling diagram that describes CPM EFT.

The progress of each stage through the project

iterations is represented by a piecewise straight line.

The slope of this line corresponds to the “production

rate” in a specific stage at each of the 6 iterations.

Horizontal segments on the progress line correspond

to work discontinuities between executions of the

same stage in successive iterations. Vertical

segments represent cases where a stage is planned

not to be performed in the corresponding iteration

(e.g., this is the case for the Requirements Review

stage (C) in the fifth iteration).

CPM EFT can be considered as an “under-estimate”

schedule that provides a minimum time bound for

the time box duration of each iteration (i.e., the

earliest time that iteration 1 should be completed is

before 18 weeks, iteration 2 should be before 24

weeks etc.). The danger with an under-estimate

schedule is the effect on software quality, since

obtaining partial software deliveries, as early as

possible, could affect negatively the software

quality. CPM EFT is actually a baseline schedule for

the rest of the analysis. It is a “too optimistic”

ICSOFT 2008 - International Conference on Software and Data Technologies

228

project plan that results in minimum values of

completion times for all iterations.

Project Duration: 48 weeks

Work breaks:

Stage A: 0 weeks

Stage B: 19

Stage C: 16

Stage D: 1

Stage E: 0

Stage F: 10

Total gaps: 46 weeks

Completion Times:

Iteration 1: 18 weeks

Iteration 2: 24

Iteration 3: 30

Iteration 4: 36

Iteration 5: 42

Iteration 6: 48

CPM Schedule - Earliest Start / Finish Times

0 4 8 12162024283236404448

Time

Iteration

Figure 2: CPM Earliest Start/Finish Time – CPM EFT.

Next, the R&D management considers scheduling

tasks according to their Latest Start (LS) times, as it

is demonstrated in Figure 3. CPM LS schedule is

obtained by pushing stages to their latest start times

and transferring work discontinuities from the last

project stages to those in the beginning.

The LP model can be solved towards the objective

of total work discontinuity minimization. This is

achieved by introducing the 48 weeks of CPM

duration in the global objective function and setting

all f

equal to 1 and all c

equal to 0. The resulting

schedule is shown in Figure 4 (CPM WD). The

minimum project duration of 48 weeks can be

achieved with a minimum of 26 weeks of work

discontinuities at stages B and C. A further reduction

of work discontinuity times is not possible without

extending the project duration beyond 48 weeks.

Iteration delays, in both CPM LS and CPM WD

schedules, have been calculated from the

corresponding minimum iteration completion time

values (i.e., the minimum time boxes) derived from

the baseline schedule (CPM EFT).

CPM Schedule – Latest Start Times

PERT SCHEDULE - LATEST START TIMES

0 4 8 12162024283236404448

Time

Units

Project Duration: 48 weeks

Work breaks:

Stage A: 6 weeks

Stage B: 20

Stage C: 22

Stage D: 0

Stage E: 0

Stage F: 0

Total gaps: 48 weeks

Completion Time

(delays from EFT):

Iteration 1: 28 weeks (+10)

Iteration 2: 32 (+8)

Iteration 3: 36 (+6)

Iteration 4: 40 (+4)

Iteration 5: 44 (+2)

Iteration 6: 48 (0)

Total delays: 30 weeks

Iteration

Figure 3: CPM Latest Start Time – CPM LS.

MINIMIZE WORK-BREAKS

UNDER CPM DURATION CONSTRAINT

0 4 8 12162024283236404448

Time

Units

Minimize Work Discontinuities

(under CPM duration constraint)

Project Duration: 48 weeks

Work breaks:

Stage A: 0 weeks

Stage B: 10

Stage C: 16

Stage D: 0

Stage E: 0

Stage F: 0

Total gaps: 26 weeks

Completion Times

(delays from EFT):

Iteration 1: 28 weeks (+10)

Iteration 2: 32 (+8)

Iteration 3: 36 (+6)

Iteration 4: 40 (+4)

Iteration 5: 44 (+2)

Iteration 6: 48 (0)

Total delays: 30 weeks

Iteration

Figure 4: Minimizing work discontinuities – CPM WD.

5.2 Calculating Net Present Values

The R&D management delivers to the company’s

management board the baseline schedule (CPM

EFT) and the two alternative schedules. The board

initially calculates the NPV for the project by

considering an one-off implementation for each

schedule. As CPM EFT minimizes the project

duration, by obtaining the software delivery as early

as possible, this selection could affect positively the

financial performance of the project, especially in

the particular project case, where the management

board reviews the first batch of iterations, to decide

continuing funding the full scale/full functionality

product development. Hence, the NPV of CPM EFT

will be an indication of the desired (ideal) expected

profit.

We also assume that time series analysis or

multivariate regression of historical or comparable

project data (past undertaken projects employing

CPM EFT, CPM LS and CPM WD schedules with

similar time constraints and overall budget) has been

applied to forecast the free cash flows at each

iteration as well as the terminal expected values of

the project for each schedule. A terminal expected

value for the whole project refers to the value of the

project at the end of the growth period (48 weeks).

For the 6 project periods (iterations/ increments),

assuming that the annualized discount rate is equal

to 12%, the compound discount rate can be

calculated equal to 12,61%, by using the following

expression:

11 −

⎟

⎠

⎞

⎜

⎝

⎛

periods

discount

We finally assume that the free cash flows at each

time box are the revenues coming from diffusion of

project results to other development company

streams. The management board estimates a 50%

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS

PERSPECTIVE

229

Table 1: NPV for CPM EFT Schedule.

Iteration

Number

0 1 2 3 4 5 6

Initial Outlay 30.000

Cash flow 10.000 15.000 16.000 14.000 13.000 11.000

Terminal

Value

120.000

Net Cash Flow 30.000 10.000 15.000 16.000 14.000 13.000 131.000

Discounted

Rate

0% 12,61% 12,61% 12,61% 12,61% 12,61% 12,61%

Present Value 30.000 8.880,2 11.829,6 11.204,4 8.706,4 7.182,3 64.247,1

Net Present

Value

82.050

probability for the software product marketing

success, due to market uncertainty and the very strict

estimate of the development duration (48 weeks).

The NPV calculation for CPM EFT (Table 1) results

in an expected revenue discounted by 50% (the

success probability), that is equal to 41.025€

(82.050€ x 0.5), a 50% discount of the initial outlay

that is equal to 15.000€ (30.000€ x 0.5), and a final

expected value for CPM EFT that is equal to

26.025€ (41.025€ - 15.000€). Accordingly, the NPV

calculation for CPM LS (Table 2) results in an

expected revenue that is equal to 35.620,1€

(71.240,3€ x 0.5) and a final expected outlay that is

equal to 15.000€ (30.000€ x 0.5). Thus, the expected

value for CPM LS is equal to 20.620,1€ (35.620,1€ -

15.000€). Finally, calculating the NPV for CPM WD

(Table 3) results in an expected revenue equal to

37.784,2€ (75.568,4€ x 0.5), a final expected outlay

equal to 15.000€ (30.000€ x 0.5) and an expected

value for CPM WD that is equal to 22.784,2€

(37.784,2€ - 15.000€).

5.3 Applying Real Options

In this step, the management board considers that the

project can be deferrable and additional

development can be undertaken only if favourable

conditions are valid in the future. In terms of Real

Options, the value of two options will be evaluated

for both CPM LS and CPM WD schedules: i) to stall

development at a specific iteration (Option to

Abandon) or ii) to proceed with the full product

development (Option to Expand). In particular, the

management board examines what would be the

profits of the schedules in case when, instead of

having the project implemented continuously from

iteration 1 to iteration 6, development executes the

first two iterations and then, if there are “favourable”

conditions, the company has the option to continue

funding the project and further implement the next

four iterations. If not, then the management board

has the option to abandon the project and loose only

the initial investment for the first two iterations.

From the total amount of the initial investment

(30.000€), the management board will consider the

decision to further invest an amount of 20.000€ after

the second iteration. The initial cash outlay for the

first two iterations is considered equal to 10.000€ for

both CPM LS and CPM WD schedules.

The binomial decision tree in Figure 5 demonstrates

the real options approach to the CPM LS schedule.

The estimation of failure/success probabilities for a

software project, in terms of the economic value of

the various project decision elements, can be

performed by empirical analysis on historical data

from previous company projects. This process can

be also supported by automated instrumentation

tools (Costa et al., 2007). In our example, the

management board has estimated, when considering

the CPM LS schedule, a 33% probability of failure

for the initial project phase (iterations 1-2) and a

67% probability of success. If the management

board gives the approval for the additional 20.000€

fund, then it is estimated a 25% probability of failure

and a 75% probability of success. The future cash

flows for the project under the CPM LS schedule are

presented in Table 4. The expected outlay of the

option to abandon is equal to 3.300€ (10.000€ x

0.33), while the expected outlay of the option to

expand is equal to 5.100€ (30.000€ x 0.17). The

expected revenue for CPM LS has been previously

calculated by NPV analysis that is equal to

35.620,1€. Thus, the expected final value for CPM

LS is equal to 27.220,1€ (35.620,1€ - 8.400€).

ICSOFT 2008 - International Conference on Software and Data Technologies

230

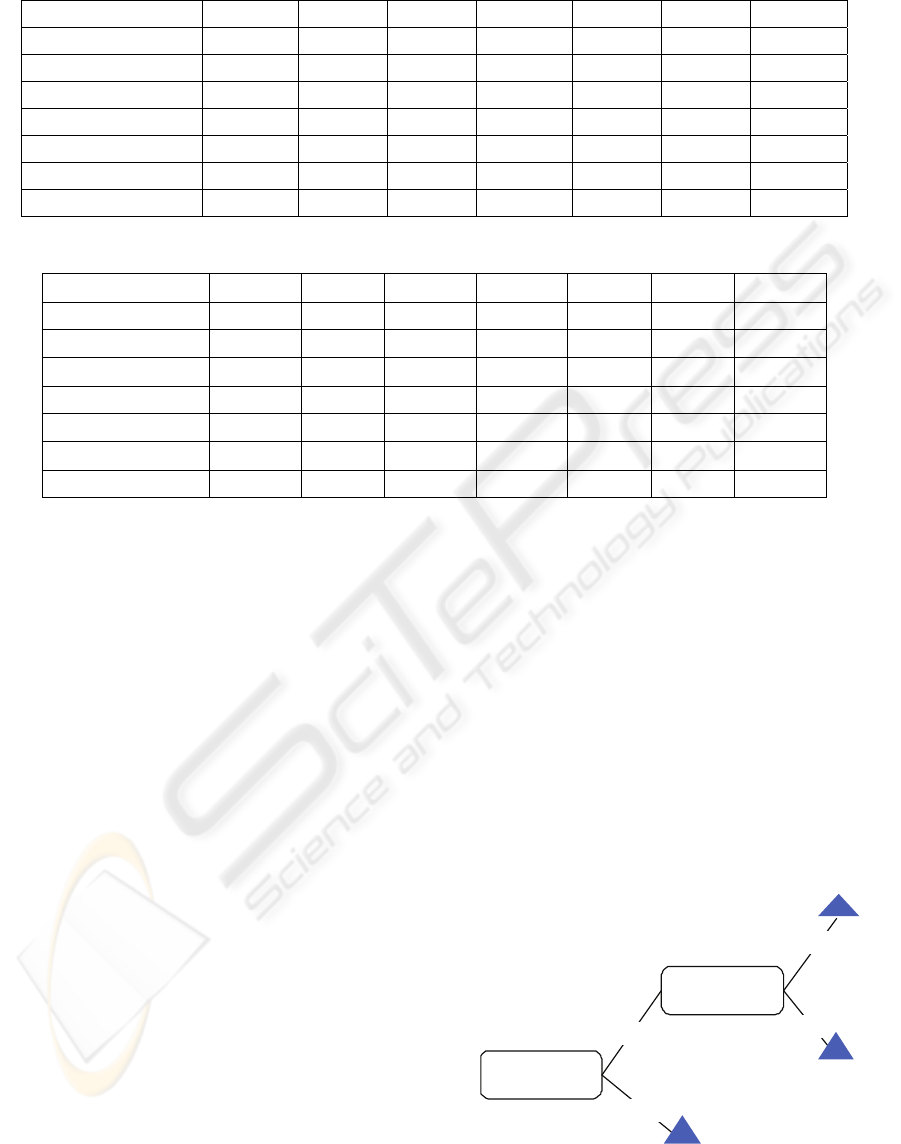
Table 2: NPV for CPM LS Schedule.

Iteration Number 0 1 2 3 4 5 6

Initial Outlay 30.000

Cash flow 10.000 12.000 15.000 12.000 11.000 10.000

Terminal Value 110.000

Net Cash Flow 30.000 10.000 12.000 15.000 12.000 11.000 120.000

Discounted Rate 0% 12,61% 12,61% 12,61% 12,61% 12,61% 12,61%

Present Value 30.000 8.880,2 9.463,7 10.504,2 7.462,6 6.077,3 58.852,3

Net Present Value 71.240,3

Table 3: NPV for CPM WD Schedule.

Iteration Number 0 1 2 3 4 5 6

Initial Outlay 30.000

Cash flow 10.000 13.000 16.000 14.000 13.000 11.000

Terminal Value 110.000

Net Cash Flow 30.000 10.000 13.000 16.000 14.000 13.000 121.000

Discounted Rate 0% 12,61% 12,61% 12,61% 12,61% 12,61% 12,61%

Present Value 30.000 8.880,2 10.252,3 11.204,4 8.706,4 7.182,3 59.342,8

Net Present Value 75.568,4

Similarly, the tree in Figure 6 examines both real

options, when considering CPM WD schedule. The

management board acknowledges an 80%

probability of success for the initial project phase

(iterations 1-2), and hence a 20% probability of

failure. The reason for this optimistic estimate is that

CPM WD presents less “slack times” and thus may

result in achieving a high level of work continuity

and a smooth flow of development work over the

initial two iterations. If the board takes the option to

expand and invest the additional 20.000€ fund, then

it is estimated a 25% probability of failure and a

75% probability of success.

Table 5 presents the estimated future cash flows for

the project under the CPM WD schedule. The

expected outlay of the option to abandon is equal to

2.000€ (10.000€ x 0.20), while the expected outlay

of the option to expand is equal to 9.000€ (30.000€ x

0.30). The expected revenue for CPM WD has been

calculated previously by the NPV analysis that is

equal to 37.784,2€. Therefore, the expected final

value for CPM WD is equal to 26.784,2€ (37.784,2€

- 11.000€).

5.4 Retrospect the Analysis

We notice that applying the real options and giving

the management board a different view of the

potential risks - and hence the flexibility to adjust

the incremental delivery plan - we have a totally

different suggestion compared to the corresponding

indication produced by calculating NPVs. With

NPV, the management board is advised to select the

CPM WD schedule, as it is expected to result in an

amount of profit equal to 22.784,2€, instead of

20.620,1€ expected from CPM LS. With Real

Options though, the decision should be different.

Estimating the risks accordingly, the expected value

of CPM WD (26.784,2€) is less than this of CPM LS

(27.220,1€). This can be explained by closely

considering the two schedules’ characteristics

(Figures 3 & 4). Even though, both CPM WD and

CPM LS present the same iteration delays, CPM LS

due to its latest pushing time characteristic, may

provide a better managerial flexibility.

Figure 5: Options for CPM LS.

Iterations

(

Iterations

(

)

67%

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS

PERSPECTIVE

231

Table 4: Cash Flows for the Project under the CPM LS schedule.

Iteration Number 0 1 2 2 3 4 5 6

Initial Outlay 10.000 20.000

Cash flow 10.000 12.000 15.000 12.000 11.000 10.000

Terminal Value 110.000

Net Cash Flow -10.000 10.000 12.000 -20.000 15.000 12.000 11.000 120.000

Discounted Rate 0% 12,61% 12,61% 0% 12,61% 12,61% 12,61% 12,61%

Present Value -10.000 8.880,2 9.463,7 -20.000 10.504,2 7.462,6 6.077,3 58.852,3

Table 5: Cash Flows for the Project under the CPM WD schedule.

Iteration Number 0 1 2 2 3 4 5 6

Initial Outlay 10.000 20.000

Cash flow 10.000 13.000 16.000 14.000 13.000 11.000

Terminal Value 110.000

Net Cash Flow -10.000 10.000 13.000 -20.000 16.000 14.000 13.000 121.000

Discounted Rate 0% 12,61% 12,61% 0% 12,61% 12,61% 12,61% 12,61%

Present Value -10.000 8.880,2 10.252,3 -20.000 11.204,4 8.706,4 7.182,3 59.342,8

Figure 6: Options for CPM WD.

Pushing stages to their LS times transfers

coordination (work discontinuity) from the last

iteration stages to those in the beginning of the

project. Consider, for example, that in both

schedules the work discontinuities have been

transferred from the final iteration stages (stages D,

E and F) to those in the beginning (stages A, B and

C). However, the total work discontinuity time for

stages A, B and C in CPM LS is equal to 48 weeks,

while the same stages in CPM WD present a total

work-discontinuity time equal to 26 weeks. Thus,

the R&D management has more time to review risky

situations upon unexpected changes and

coordination delays earlier in the project (e.g.,

remove defects and consider requirements changes).

Furthermore, the objective of minimizing work

discontinuities may negatively affect the

coordination time between project stages. On one

hand, this may improve the smooth flow of

development work, on the other, the risk of having a

low defect removal efficiency in early iteration

stages is increasing (and consequently in later

stages). In general, establishing the right

coordination policy is a difficult and high risky task

(Mookerjee and Chiang, 2002). Coordination is

affected by dynamic factors that cannot be easily

predicted due to the differences in the intensity of

coordination needed at different project stages.

Moreover, coordination is highly dependent on the

development team's learning curve. Since, in

general, the development teams’ knowledge of the

system improves with time, a lot of coordination

may be needed early in the project.

6 CONCLUSIONS

In this study, we extended the results of previous

work on multi objective analysis of scheduling

iterative/incremental software projects which follow

timeboxing disciplines. By applying Real Options,

we moved forward the optimization decision of the

release planning process to perform the cost

valuation of different scheduling decisions. We

argued for the proposed approach by examining the

risk of two options, the option to stall (abandon) an

incremental delivery plan at a pre-defined iteration

Iterations

(

)

80%

ICSOFT 2008 - International Conference on Software and Data Technologies

232

and the option to continue iterations (expand

development) and deliver the full system

functionality.

To demonstrate the usefulness of the approach, we

calculated the static discounted Net Present Values

of selected schedules in a project case study, and

then we compared these values with those resulting

from the Real Options application. The analysis

results highlighted how Real Options can provide

increased managerial flexibility as they force

management to consider investment risks associated

with the alternative project scheduling decisions, as

unexpected events in one stage or iteration may

affect not only the iteration completion/delivery

times but also the work continuity in project

resources. Furthermore, this study discussed that

applying Real Options can be useful to discover

knowledge concerning the value of candidate

schedules to be adopted in iterative/incremental

projects in a retrospective manner and, thus to

enable decision makers/ project managers to better

manage the scheduling alternatives.

For future work, we are interested in moving the

approach one step forward by considering Real

Options as a possible tool to be applied in the

selection and prioritization of features to be

delivered in each software iteration/increment. It is

also our intent to experiment and apply the approach

into real scale incremental/iterative projects,

exploiting the full scope of Real Options

methodology, tools and techniques. Such exploration

will demonstrate the required input data and how

they can be collected to realize the approach in

complex software projects.

REFERENCES

Akker, J. M. van den, Brinkkemper, S., Diepen, G.,

Versendaal, J., 2008. Software Product Release

Planning through Optimization & What-If Analysis.

Information and SW Technology, 50(1-2), 101-111.

Amram, M., Kulatilaka, N., 1999. Real Options:

Managing Strategic Investment in an Uncertain

World. Harvard Business School Press, Boston,

Massachusetts.

Benaroch, M. 2002. Managing Information Technology

Risk: A Real Options Perspective. Journal of

Management Information Systems, 19(2), 43–84.

Costa, H. R., Barros, M. O., Travassos, G. H., 2007.

Evaluating Software Project Portfolio Risks. Journal

of Systems & Software, 80(1), 16-31.

EDSER, 2006. Proceedings of 8th Int. Workshop on

Economics - Driven Software Engineering Research

(EDSER). In conjunction with the 28th Int. Conf. on

Software Engineering, Shanghai, 2006, SIGSOFT-

ACM (www.cs.virginia.edu/~sullivan/EDSER-8).

Gerogiannis, V. C., Ipsilandis P. G., 2007. Multi Objective

Analysis for Timeboxing Models of Software

Development. In Proceedings of the 2nd Int. Conf. on

Software & Data Technologies, ICSOFT 2007,

Barcelona, July 2007, INSTICC Press, pp. 145-153.

Greer, D., Ruhe, D., 2004. Software Release Planning: an

Evolutionary & Iterative Approach. Information & SW

Technology, 46(4), 243-253.

Jalote, P., Palit, A., Kurien, P., Peethamber, V. T., 2004.

Timeboxing: a Process Model for Iterative Software

Development. Journal of Systems & Software, 70(1-2),

117-127.

Mookerjee, V. S., Chiang, I. R., 2002. A Dynamic

Coordination Policy for Software System

Construction. IEEE Transactions on Software

Engineering, 28(7), 684 – 694.

Myers, S. C., 1977. Determinants of Corporate Borrowing.

Journal of Financial Economics. Vol. 5(2). 147-175.

Schwartz, S., Trigeorgis, L., 2000. Real Options &

Investment under Uncertainty: Classical Readings and

Recent Contributions. MIT Press Cambridge,

Massachusetts.

Stapleton, J., 2003. DSDM: Business Focused

Development. Addison-Wesley.

Sullivan, K., Chalasani, P., Jha, S., & Sazawal, V., 1999.

Software Design as an Investment Activity: a Real

Options Perspective. In Trigeorgis, L. (ed.), Real

Options & Business Strategy: Applications to

Decision Making, Risk Books, 215-261.

Tiwana, A., Keil, M., Fichman, R, 2006. Information

Systems Project Continuation in Escalation Situations:

a Real Options Model. Decision Sciences, 37(3), 357-

391.

Wu, L. C., Ong,C. S., Hsu, Y.W., 2007. Active ERP

Implementation Management: a Real Options

Perspective. Journal of Systems & Software. In Press

(doi:10.1016/j.jss.2007.10.004).

EVALUATING SCHEDULES OF ITERATIVE/INCREMENTAL SOFTWARE PROJECTS FROM A REAL OPTIONS

PERSPECTIVE

233