
EXTENSIONS TO THE OLAP FRAMEWORK
FOR BUSINESS ANALYSIS
Emiel Caron
a
a
Erasmus University Rotterdam, ERIM Institute of Advanced Management Studies
P.O. Box 1738, 3000 DR, Rotterdam, The Netherlands
Hennie Daniels
a,b
b
Center for Economic Research, Tilburg University
P.O. Box 90153, 5000 LE, Tilburg, The Netherlands
Keywords: Business Intelligence, Multi-dimensional databases, OLAP, Explanation, Sensitivity analysis.
Abstract: In this paper, we describe extensions to the OnLine Analytical Processing (OLAP) framework for business
analysis. This paper is part of our continued work on extending multi-dimensional databases with novel
functionality for diagnostic support and sensitivity analysis. Diagnostic support offers the manager the
possibility to automatically generate explanations for exceptional cell values in an OLAP database. This
functionality can be built into conventional OLAP databases using a generic explanation formalism, which
supports the work of managers in diagnostic processes. The objective is the identification of specific
knowledge structures and reasoning methods required to construct computerized explanations from multi-
dimensional data and business models. Moreover, we study the consistency and solvability of OLAP
systems. These issues are important for sensitivity analysis in OLAP databases. Often the analyst wants to
know how some aggregated variable in the cube would have been changed if a certain underlying variable is
increased ceteris paribus (c.p.) with one extra unit or one percent in the business model or dimension
hierarchy. For such analysis it is important that the system of OLAP aggregations remains consistent after a
change is induced in some variable. For instance, missing data, dependency relations, and the presence of
non-linear relations in the business model can cause a system to become inconsistent.
1 INTRODUCTION
Today’s OLAP databases have limited capabilities
for diagnostic support and sensitivity analysis. The
diagnostic process is now carried out mainly
manually by business analysts, where the analyst
explores the multi-dimensional data to spot
exceptions visually, and navigates the data with
operators like drill-down, roll-up, and selection to
find the reasons for these exceptions. It is obvious
that human analysis can get problematic and error-
prone for large data sets that commonly appear in
practise. For example, a typical OLAP data set has
five to seven dimensions and average of three levels
hierarchy on each dimension and aggregates more
than a million records. The goal of our research is to
largely automate these manual diagnostic discovery
processes (Caron and Daniels, 2007). This func-
tionality can be provided by extending the
conventional OLAP system with an explanation
formalism, which supports the work of human
decision makers in diagnostic processes. Here
diagnosis is defined as finding the best explanation
of unexpected behaviour (i.e. symptoms) of a system
under study (Verkooijen, 1993). This definition
captures the two tasks that are central in problem
diagnosis, namely problem identification and
explanation generation. It assumes that we know
which behaviour we may expect from a correctly
working system, otherwise we would not be able to
determine whether the actual behaviour is what we
expect or not.
In addition, we describe a novel OLAP
operator that supports the analyst in answering
typical managerial analysis questions in an OLAP
data cube. For example, an analyst might be
240
Caron E. and Daniels H. (2008).
EXTENSIONS TO THE OLAP FRAMEWORK FOR BUSINESS ANALYSIS.
In Proceedings of the Third International Conference on Software and Data Technologies - ISDM/ABF, pages 240-247
DOI: 10.5220/0001895102400247
Copyright
c
SciTePress

interested in the questions: How is the profit on the
aggregated year level affected when the profit for
product P1 is changed in the first quarter in The
Netherlands? Or how is the profit in the year 2007
for a certain product affected when its unit price is
changed (c.p.) in the sales model? Such questions
might be ‘dangerous’, when the change is not caused
by a variable in the base cube, but by a variable on
some intermediate aggregation level in the cube. The
latter situation makes the OLAP database inconsis-
tent. Our novel OLAP operator corrects for such
inconsistencies such that the analysts can still carry
out sensitivity analysis in the OLAP database. Our
research shows that consistency and solvability of
OLAP databases are important criteria for sensitivity
analysis in OLAP databases.
1.1 OLAP Introduction
OLAP databases are a popular business intelligence
technique in the field of enterprise information
systems for business analysis and decision support.
OLAP not only integrates the management
information systems (MIS), decision support
systems (DSS), and executive information systems
(EIS) functionality of the earlier generations of
information systems, but goes further and introduces
spreadsheet-like multi-dimensional data views and
graphical presentation capabilities (Koutsoukis et
al., 1999). OLAP systems have a variety of
enterprise functions. Finance departments use OLAP
for applications such as budgeting, activity-based
costing, financial performance analysis, and
financial modelling. Sales analysis and forecasting
are two of the OLAP applications found in sales
departments.
The core component of an OLAP system is
the data warehouse, which is a decision-support
database that is periodically updated by extracting,
transforming, and loading data from several On-Line
Transaction Processing (OLTP) databases. The
highly normalized form of the relational model for
OLTP databases is inappropriate in an OLAP
environment for performance reasons. Therefore,
OLAP implementations typically employ a star
schema, which stores data de-normalized in fact
tables and dimension tables. The fact table contains
mappings to each dimension table, along with the
actual measured data. In a star scheme data is
organized using the dimensional modelling
approach, which classifies data into measures and
dimensions. Measures like, for example, sales,
profit, and costs figures, are the basic units of
interest for analysis. Dimensions correspond to
different perspectives for viewing measures.
Examples dimensions are a product or a time
dimension. Dimensions are usually organized as
dimension hierarchies, which offer the possibility to
view measures at different dimension levels (e.g.
month
≺ quarter ≺ year is a hierarchy for the Time
dimension). Aggregating measures up to a certain
dimension level, with functions like sum, count, and
average, creates a multidimensional view of the data,
also known as the data cube. A number of data cube
operations exist to explore the multidimensional data
cube, allowing interactive querying and analysis of
the data.
The remainder of this paper is organized as
follows. Section 2 introduces our notation for multi-
dimensional models, followed by a description of
models appropriate for OLAP problem identification
in Section 3. In Section 4 the explanation formalism
is extended for multi-dimensional data in order to
automatically generate explanations. In section 5 we
show that systems of OLAP equations are consistent
and have a unique solution. Subsequently, we apply
this result for sensitivity analysis in the OLAP
context. Finally, conclusions are discussed in
Section 6.
2 NOTATION AND EQUATIONS
Here we use a generic notation for multi-
dimensional data schemata that is particularly
suitable for combining the concepts of measures,
dimensions, and dimension hierarchies as described
in (Caron and Daniels, 2007). Therefore, we define a
measure y as a function on multiple domains:
12
12
12
:
nn
ii i i
ii
n
yDD D××× →
…
… R
(1)
Each domain
i
D has a number of hierarchies ordered
by
max
01
i
kk k
DD D≺≺…≺ , where
0
k
D
is the lowest
level and
max
i
k
D
is the highest level in
max
i
k
D
. A
dimension’s top level has a single level instance
{
}
max
All
i
k
D = . For example, for the time dimension
we could have the following hierarchy
01
TT≺
2
T≺ , where
{
}
2
T All-T= ,
{
}
1
T 2000,2001= , and
{
}
0
Q1,Q2,Q3,Q4T = . A cell in the cube is denoted
by
12
(, , , )
n
dd d… , where the 's
k
d are elements of
the domain hierarchy at some level, so for example
(2000, Amsterdam, Beer) might be a cell in a sales
cube. Each cell contains data, which are the values
of the measures
y like, for example,
211
sales (2000,
Amsterdam, Beer). The measure’s upper indices
EXTENSIONS TO THE OLAP FRAMEWORK FOR BUSINESS ANALYSIS
241

indicate the level on the associated dimension
hierarchies. If no confusion can arise we will leave
out the upper indices indicating level hierarchies and
write sales(2000, Amsterdam, Beer). Furthermore,
the combination of a cell and a measure is called a
data point. The measure values at the lowest level
cells are entries of the
base cube. If a measure value
is on the base cube level, then the hierarchies of the
domains can be used to aggregate the measure
values using aggregation operators like SUM,
COUNT, or, AVG.
By applying suitable equations, we can alter
the level of detail and map low level cubes to high
level cubes and vice versa. For example, aggregating
measure values along the dimension hierarchy (i.e.
rollup) creates a multidimensional view on the data,
and de-aggregating the measures on the data cube to
a lower dimension level (i.e. drilldown), creates a
more specific cube.
Here we investigate the common situation
where the aggregation operator is the summarization
of measures in the dimension hierarchy. So
y is an
additive measure or OLAP equation (Lenz and
Shoshani, 1997) if in each dimension and hierarchy
level of the data cube:
11 1
1
(,,) (,,)
qn qn
J
ii i ii i
j
j
yaya
+
=
=
∑
…… ……
…… … …
(2)
where
1q
k
aD
+
∈ ,
q
j
k
aD∈ , q is some level in the
dimension hierarchy, and
J represents the number of
level instances in
q
k
D . An example equation
corresponding to two roll-up operations reads:
212
420
102
11
sales (2001, All-Locations, Beer)
sales (2001.Q ,Country , Beer).
jk
jk
==
=
∑∑
Furthermore, we assume that a business model
M is
given representing relations between measures.
These relations can be derived from many domains,
like finance, accounting, logistics, and so forth.
Relations are denoted by
12
12
12
12
(, , , )
((,,,))
n
n
ii i
n
ii i
n
yddd
f
dd d
=
x
…
…
…
…
(3)
where
1
(, , )
n
x
x=x … , and y are measures defined
on the same domains. Business model equations
usually hold on equal aggregation levels in the data
cube, therefore we may leave out upper indices if no
confusion can arise. In Table 1, the business model
with quantitative relations from an example financial
database is presented.
Table 1: Example business model M.
1. Gross Profit = Revenues - Cost of Goods
2. Revenues = Volume Unit Price
3. Cost of Goods = Variable Cost + Indirect Cost
4. Variable Cost = Volume · Unit Cost
5. Indirect Cost = 30% · Variable Cost
3 PROBLEM IDENTIFICATION
There are many ways to identify exceptional cells in
multidimensional data with normative models. The
simplest way is pairwise comparison between two
cells. In general, only the cells on the same
aggregation levels will be used for obvious reasons,
like the measurement scale of the variable. For
example, we can compare sales (2000,Germany,All-
Products) with the sales of the previous year, norm(
sales(1999,Germany,All-Products)), as an historical
norm value. Another common norm values is the
expected value
y
of a cell computed using a context
of the cell:
1
1
(,,) (,,)
J
j
j
J
yya
=
+=
∑
…… … …
(4)
and for the average over all domains we write
(,, , )y ++ +… . Expected values are based on
statistical models. A huge variety of statistical
models exists for two-way tables, three-way tables,
etc., see Scheffé (1959) and Tukey (1988). Here we
only consider two models namely the additive multi-
way ANOVA model for continuous data and the
model of independence for category data. For a
continuous data set, in the situation of only two
dimensions, we can write the expected value as an
additive function of three terms obtained from the
possible aggregates of the table:
12 1 2
ˆ
( , ) ( ,) (, ) (,).yd d yd y d y=+++−++
(5)
The residual of a model is defined as
y
Δ=
ˆ
norm
yy yy−=−. If we normalize the residual of the
model by the standard deviation of the cell, we get
the normalized residual
/
s
y
σ
=Δ , where
ˆ
y is com-
puted with the same statistical model applied to a
certain context of the cell and
σ
is the standard
deviation in the same context. The problem of
looking for exceptional cell values is equivalent to
the problem of looking for exceptional normalized
residuals, also known as symptom identification.
The actual data point is
a
y , and
r
y is the norm
object. When a statistical model is used as a
normative model
ˆ
r
yy= . Furthermore, the larger
ICSOFT 2008 - International Conference on Software and Data Technologies
242

the absolute value of the normalized residual, the
more exceptional a cell is. A data point is a symptom
or surprise value (Sarawagi, 1998) if
s
is higher
than some user-defined threshold
δ
. When s
δ
> ,
the cell is a “high” exception; and when
s
δ
<− , the
cell is a “low” exception.
4 EXPLANATION
4.1 Explanation Method
Our exposition on diagnostic reasoning and causal
explanation is largely based on Feelders and Daniels
(1993) notion of explanations, which is essentially
based on Humpreys’ notion of aleatory explanations
(1989) and the theory of explaining differences by
Hesslow (1983). The canonical form for causal
explanations is taken from Feelders and Daniels
(1993, 2001):
, , because , despite .aFr C C
+−
〈〉
(6)
where
,,aFr〈〉
is the symptom to be explained, C
+
is non-empty set of contributing causes, and C
–
a
(possibly empty) set of counteracting causes. The
explanation itself consists of the causes to which C
+
jointly refers. C
–
is not part of the explanation, but
gives a clearer notion of how the members of C
+
actually brought about the symptom. The
explanandum is a three-place relation between an
object a (e.g. the ABC-company), a property F (e.g.
having a low profit) and a reference class r (e.g.
other companies in the same branch or industry).
The task is not to explain why a has property F, but
rather to explain why a has property F when the
other members of r do not. This general formalism
for explanation constitutes the basis of the
framework for diagnosis in an OLAP context.
4.2 Influence Measure
If +y is a symptom we want to explain the
difference
ar
yy yΔ= − where
r
y is a reference
value of the cell under study. An explanation is
given using relations of the business model or
relations of the dimension hierarchies. Then the
influence of
i
x
on
y
Δ
is defined as (Feelders and
Daniels, 1993):
inf( , ) ( , )
ra r
iii
x
yf x y
−
=−x
(7)
where
(,)
ra
ii
f
x
−
x denotes the value of ()
f
x with all
variables evaluated at their norm values, except the
measure
i
x
. Here
r
i
x
is a reference value for the
measure
i
x
. The correct interpretation of the mea-
sure depends on the form of the function f; the
function has to satisfy the so-called conjunctiveness
constraint. This constraint captures the intuitive
notion that the influence of a single variable should
not turn around when it is considered in conjunction
with the influence of other variables.
In the dimension hierarchy, f is additive by
definition, it follows from (2) that:
111
11
;;
inf( ( , , ), ( , , ))
(,,) (,,).
qn q n
qn qn
ii i ii i
j
ai i i ri i i
jj
yay a
yaya
−
=
−
…… … …
…… ……
…… ……
…… ……
(8)
When explanation is supported by a business model
equation the set of contributing (counteracting)
causes C
+
(C
–
) consists of measures x
i
of the
business model with:
inf( , ) 0
i
xy y×Δ > (0)< . In
words, the contributing causes are those variables
whose influence values have the same sign as
∂y,
and the counteracting causes are those variables
whose influence values have the opposite sign. If
explanation is supported by the dimension hierarchy,
the set of contributing (counteracting) causes C
+
consists of the set of child instances
j
a of
dimension level
q
i out of the hierarchy of a specific
dimension with:
111
inf( ( , , ), ( , , )) 0
qn q n
ii i ii i
j
yay ay
−
×Δ >
…… … …
…… ……
4.3 Filtering Explanations
Because every applicable equation yields a possible
explanation, the number of explanations generated
for a single symptom can be quite large. Especially
when explanations are chained together to form a
tree of explanations we might get lost in many
branches. In order to leave insignificant influences
out of the explanation we introduce three methods.
Firstly, in the problem identification phase the
analyst distillates a set of symptoms. This means that
if a cell does not have a large deviating value –
based on some statistical model or defined by a user
– it is not identified as a symptom and therefore not
considered for explanation generation. Secondly,
small influences are left out in the explanation by a
filter. The set of causes is reduced to the so-called
parsimonious set of causes. The parsimonious set of
contributing causes
p
C
+
is the smallest subset of the
set of contributing causes, such that its influence on
y exceeds a particular fraction (T
+
) of the influence
of the complete set. The fraction T
+
is a number
EXTENSIONS TO THE OLAP FRAMEWORK FOR BUSINESS ANALYSIS
243

between 0 and 1, and will typically 0.85 or so. A
third way to reduce the number of explanations is by
applying a measure of specificity for each applicable
equation. This measure quantifies the “interesting-
ness” of the explanation step. The measure is
defined as:
# possible causes
specificity =
# actual causes
(9)
The number of possible causes is the number of
right-hand side elements of each equation, and the
number of actual causes is the number of elements in
the parsimonious set of causes. Using this measure
of specificity we can order the explanation paths
from specific to general and if desired only list the
most specific steps.
4.4 Multi-level Explanation
The explanation generation process for multidimen-
sional data is quite similar to the knowledge mining
process at multiple dimension levels. Especially, the
idea of progressive deepening seems very “natural”
in the explanation generation process; start symptom
detection on an aggregated level in the data cube and
progressively deepen it to find the causes for that
symptom at lower levels of the dimension hierarchy
or business model. This idea we will adopt for so-
called multi-level explanations. In the previous parts,
we have discussed “one-level” explanations;
explanations based on a single relation from the
business model or dimension hierarchy. For
diagnostic purposes, however, it is meaningful to
continue an explanation of
∂y = q, by explaining the
quantitative differences between the actual and norm
values of its contributing causes. In multi-level
explanation this process is continued until a
parsimonious contributing cause is encountered that
cannot be explained further because:
• the business model equations do not contain an
equation in which the contributing cause appears
on the left-hand side.
• the dimension hierarchies do not contain a drill-
down equation in which the contributing cause
appears on the left-hand side.
The result of this process is an explanation tree of
causes, where y is the root of the tree with two types
of children, corresponding to its parsimonious
contributing and counteracting causes respectively.
A node that corresponds to a parsimonious
contributing cause is a new symptom that can be
explained further, and a node that corresponds to a
parsimonious counteracting cause has no successors.
In the explanation tree there are numerous
explanation paths from the root to the leaf nodes.
This implies that many different explanations can be
generated for a symptom. In most practical cases one
would therefore apply the pruning methods
discussed above yielding a comprehensive tree of
the most important causes.
4.5 Making Hidden Causes Visible
The phenomenon that the effects of two or more
lower-level variables in the dimension hierarchy (or
business model) cancel each other out so that their
joint influence on a higher-level variable in the
business model is partly or fully neutralized is quite
common in multidimensional databases. For the top-
down explanation generation process this means that
in some data sets possible significant causes for a
symptom will not be detected when cancelling-out
effects are present. These non-detected causes by
multi-level explanation are called hidden causes. In
theory, cancelling-out effects may occur at every
level in the dimension hierarchy. Of course, analysts
would like to be informed about significant hidden
causes, and would consider an explanation tree
without mentioning these causes as incomplete and
not accurate.
Here a multi-step look-ahead method is
developed for detecting hidden causes. In short, the
look-ahead method is composed of two consecutive
phases: an analysis (1) and a reporting phase (2). In
the analysis phase the explanation generation
process starts, similar as for maximal explanation,
with the root equation in the dimension hierarchy by
determining parsimonious causes. However, instead
of proceeding with strictly parsimonious causes, all
non-parsimonious contributing and counteracting
causes are investigated for possible cancelling-out
effects at a specific (lower) level in the hierarchy. In
multi-step look-ahead, a successor of variable
1
(,,)
qn
ii i
j
ya
……
…… is a hidden cause if its influence
on
11
(,,)
qn
ii i
ya
−
……
…… is significant after
substitution, when the influence of variable
1
(,,)
qn
ii i
j
ya
……
…… of (2) on
11
(,,)
qn
ii i
ya
−
……
…… is
not significant. These hidden causes are made
visible by means of function substitution, where all
the lower-level equations at level
i
k
D in the
dimension hierarchy are substituted into the higher-
level equation under consideration for explanation.
In the reporting phase the explanation tree is updated
when hidden causes are detected by the multi-level
look-ahead method.
ICSOFT 2008 - International Conference on Software and Data Technologies
244

5 SENSITIVITY ANALYSIS
Sensitivity analysis in the OLAP context is related to
the notion of comparative statics in economics.
Where the central issue is to determine how changes
in independent variables affect dependent variables
in an economic model. Comparative statics is
defined as the comparison of two different
equilibrium states solutions, before and after change
in one of the independent variables, keeping the
other variables at their original values. The basis for
comparative statics is an economic model that
defines the vector of dependent variables
y as
functions of the vector of independent variables
x. In
this paper we apply comparative statics in the OLAP
context where we have a system of linear equations
with dependent variables on an aggregated level of
the cube, called non-base variables and independent
variables on the base level, called base variables.
5.1 Aggregation Lattice
An OLAP cube represents a system of additive
equations in the form of a aggregation lattice. The
top of the lattice is the single non-base variable
max max max
ii i
y
…
and the bottom of the the lattice is
represented by the base variables
00 0
x
…
. The upset
of a base variable in the lattice represents non-base
variables on specific levels of aggregation (i.e.,
summarization) in the OLAP cube. For example, the
non-base variable
12
(1)
pn
ii i i
y
+……
is a parent of the non-
base variable
12 pn
ii i i
y
……
, somewhere in the lattice. In
In the OLAP cube roll-ups can be alternated
from one dimension to the next, resulting in multiple
paths from a base variable to a non-base variable in
the aggregation lattice. For example,
110 0
y
…
is a
common ancestor of
000 0
x
…
via parent
100 0
y
…
and
parent
010 0
y
…
. In addition, in the lattice the partial
ordering within a single dimension hierarchy is
preserved. In other words, it is not allowed to skip
intermediate dimension levels. Thus, a parent in the
lattice is on level
12
(1)
p
n
ii i i+…… and a child on
level
12 pn
ii i i……
and possible other ancestors are
on level
12
()
p
n
ii i m i+…… and have a connection
with the child via the parent.
The length of a path from a non-base variable
12 n
ii i
y
…
in the lattice to a base variable
00 0
x
…
is
12 n
ii i++ +… . Obviously, the sum of the indices of
a non-base variable corresponds with the number of
aggregations carried out. Every non-base variable in
a system of OLAP equations is the result of a
sequence of aggregations in the lattice structure.
Although there are often multiple paths in the lattice
from a non-base variable to a base variable, each
non-base variable corresponds with a single equation
expressed in a unique set of base variables. The
multiple paths are just the result of the same
summarization, however carried out in a different
order. This can be verified by substituting all
equations in the downset of a non-base variable from
level
12 n
ii i++ +… to the base level. Suppose we
have the non-base variable
12
12
(, , , )
n
i
ii
n
y
dd d
…
…
somewhere in the aggregation lattice. This variable
is the linear combination of a unique set of base
variables, denoted by:
12
12
00 0
11 1
00 0
11 1
00 0
11 1
(, , , )
(,,, )
(,,, )
...
(,,, )
n
i
ii
n
KL W
kl w
kl w
LK W
kl w
lk w
WL K
kl w
wl k
yddd
xabz
xabz
xabz
== =
== =
== =
=
=
=
=
∑∑ ∑
∑∑ ∑
∑∑ ∑
…
…
…
…
…
……
……
……
(10)
Because of (10) it can be shown that the OLAP
aggregation lattice always a unique solution for the
non-base variables for a given a set of base
variables.
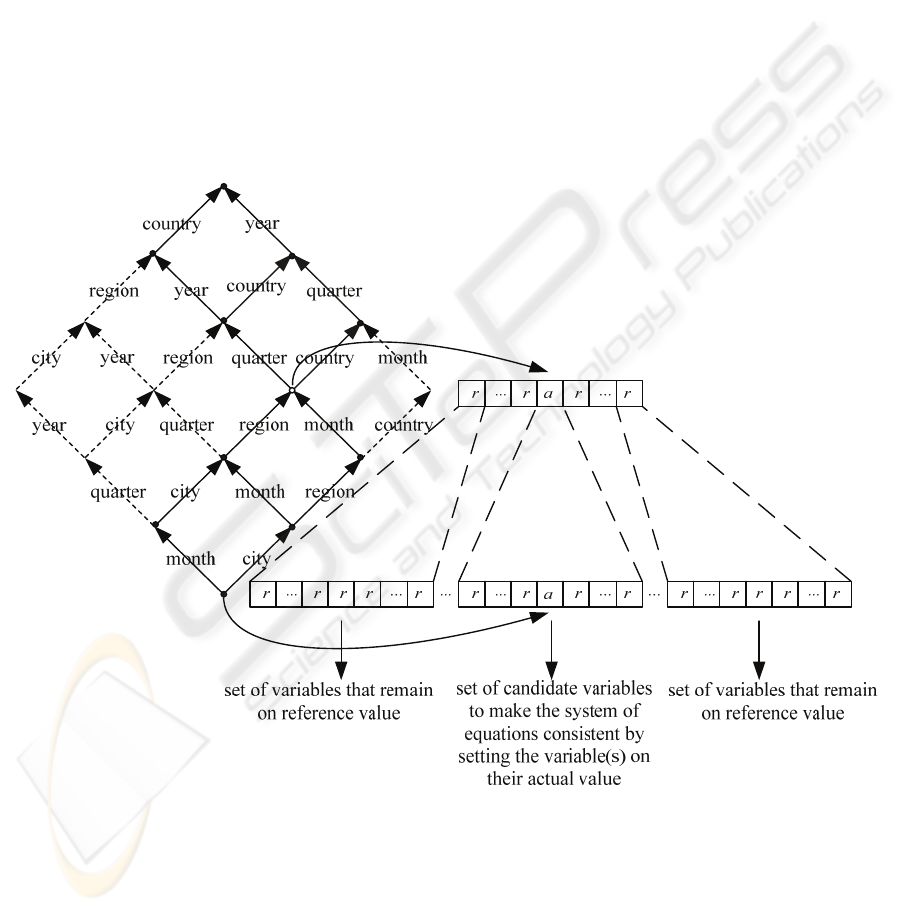
In figure 1 of the Appendix, an example
aggregation lattice is given for the variable sales
(
12
ii
y ) from some sales database, where the first
index represents the hierarchy for the Time (T)
dimension with the levels T
3
[All-T], T
2
[Year],
T
1
[Quarter] and T
0
[Month], and the second index
represents the Location (L) dimension with the
levels L
3
[All-L], L
2
[Country], T
1
[Region] and
T
0
[City]. In the lattice the variable
12
y , which has a
number of data instances, has instances of the
variables {
22
y
,
13
y
,
23
y
,
32
y
,
33
y
} in its upset and
instances of the variables {
11
y ,
02
y ,
10
y ,
01
y ,
00
x
} in
its downset. All non-base variables in the lattice are
aggregated from instances of the base variables
00
(month, city)x . It can easily be shown with
function substitution that each non-base variable in
the example lattice can be expressed in a unique set
of base variables.
EXTENSIONS TO THE OLAP FRAMEWORK FOR BUSINESS ANALYSIS
245

5.2 Sensitivity Analysis Correction
Because of the arguments above, a change in a
single base variable c.p. in the aggregation lattice
will result in a new unique solution for the non-base
variables. The influence of a base variable on some
aggregated non-base variable is given by:
12
00 0
00 0 00 0
inf( ( , , ), ( , , ))
(, ,) (,,)
n
ii i
j
ar
jj
xay a
xaxa
=
−
…
…
……
…… ……
…… ……
(11)
If a non-variable
1
(,,)
qn
ii i
j
ya
……
…… is changed with
some magnitude c.p. the aggregation lattice will
obviously become inconsistent because its downset
variables are not changed accordingly. However, the
partial system of equations representing its upset is
still consistent and the influence of a non-base
variable on some non-base variable in its upset is
given by equation (8). To make this type of
sensitivity analysis useful for the complete
aggregation lattice we have to correct the downset of
the variable
1
(,,)
qn
ii i
j
ya
……
…… for the change from
each associated lower level aggregation level to the
base cube level. For the correction procedure all
variables in the downsets of siblings of
1 qn
ii i
y
……
(,,)
j
a……have to remain on their reference values
and one variable on each level of the downset of
1
(,,)
qn
ii i
j
ya
……
…… has to be corrected with the
induced change. In this procedure the variables on
the base cube level are corrected in the last step.
This step makes the OLAP aggregation lattice again
consistent after cube construction.
In figure 1, an illustration is given of the
working of the sensitivity analysis correction.
Suppose a business analyst changes a single instance
of the variable
12
y to a new actual value a while
keeping all siblings of this variable on their
reference values r. This change makes the system of
equations in the aggregation lattice inconsistent.
Now the correction procedure corrects the downsets
of instances of variable
12
y level by level, where
only descendants of the actual instance of
12
y are
considered as candidates for correction. In the last
step of the procedure the base variables are changed
accordingly to produce again a consistent system of
OLAP equations.
6 CONCLUSIONS
In this paper, we described extensions to the OLAP
framework for business analysis. Exceptional cell
values are determined based on a normative model,
often a statistical model appropriate for multi-
dimensional data. Explanation generation is
supported by the two internal structures of the
OLAP data cube: the business model and the
dimension hierarchies. Therefore, we developed a
multi-level explanation method for finding
significant causes in these structures, based on an
influence-measure which embodies a form of ceteris
paribus reasoning. This method is further enhanced
with a look-ahead functionality to detect so-called
hidden causes. The methodology as proposed uses
the concept of an explanation tree of causes, where
explanation generation is continued until a
significant contributing cause cannot be explained
further. The result of the process is a semantic tree,
where the main causes for a symptom are presented
to the analyst. Furthermore, to prevent an
information overload to the analyst, several
techniques are proposed to prune the explanation
tree.
Currently, we are working on a novel OLAP
operator that supports the analyst in answering
typical managerial questions related to sensitivity
analysis. Often the analyst wants to know how some
root variable (e.g. profit) would have been changed
if a certain lower-level successor variable (e.g. some
cost variable) is increased (ceteris paribus) with one
extra unit or one percent in the business model or
dimension hierarchy. This is related to the notion of
partial marginality and elasticity in economics. An
important related issue is that the system of
equations (e.g. a set of business model equations)
remains consistent after the influence measure is
applied on some successor variable (of the root).
Consistency in a set of OLAP equations is not trivial
because by changing a certain variable (ceteris
paribus) a (non-)linear system of equations can
become inconsistent. For instance, missing data,
dependency relations, and the presence of non-linear
relations in the business model can cause a system to
become inconsistent. It is therefore important to
investigate the criteria for consistency in the OLAP
context.
REFERENCES
E. Caron, H.A.M. Daniels, (2007). Explanation of
exceptional values in multidimensional databases.
ICSOFT 2008 - International Conference on Software and Data Technologies
246
European Journal of Operational Research, 188, 884-
897.
A.J. Feelders, “Diagnostic reasoning and explanation in
financial models of the firm”, PhD thesis, Tilburg
University (1993).
A.J. Feelders, H.A.M. Daniels, “Theory and methodolo-
gy: a general model for automated business
diagnosis”, European Journal of Operational Research,
623-637, (2001).
G. Hesslow, Explaining differences and weighting causes,
Theoria 49 (1983) 87–111.
D.C. Hoaglin, F. Mosteller, J.W. Tukey, Exploring Data
Tables, Trends and Shapes, Wiley series in
probability, New York, 1988.
P.W. Humphreys, The Chances of Explanation, Princeton
University Press, Princeton, New Jersey, 1989.
H.J. Lenz, A. Shoshani, (1997). Summarizability in OLAP
and statistical data bases, Statistical and Scientific
Database Management, 132–143.
N.S. Koutsoukis, G. Mitra, C. Lucas (1999). Adapting on-
line analytical processing for decision modelling: The
interaction of information and decision technologies,
Decision Support Systems 26 (1) 1–30.
S. Sarawagi, R. Agrawal, R. Megiddo, (1998) Discovery-
driven exploration of OLAP data cubes, in: Conf.
Proc. EDBT ’98, London, UK, pp. 168–182.
H. Scheffé, (1959) The Analysis of Variance, Wiley, New
York.
W.J. Verkooijen, (1993) Automated financial diagnosis: A
comparison with other diagnostic domains, Journal of
Information Science 19 (2), 125–135, May.
APPENDIX
33
y
32
y
23
y
22
y
21
y
31
y
13
y
12
y
30
y
03
y
20
y
11
y
02
y
10
y
01
y
00
x
Figure 1: Aggregation lattice with the dimensions Time and Location illustrating the working of the correction procedure.
EXTENSIONS TO THE OLAP FRAMEWORK FOR BUSINESS ANALYSIS
247
