
INCORPORATING SEMANTIC ALGEBRA IN THE MDA
FRAMEWORK
Paulo E. S. Barbosa, Franklin Ramalho, Jorge C. A. de Figueiredo and Antonio D. dos S. Junior
Universidade Federal de Campina Grande, Departamento de Sistemas e Computac¸˜ao
Campina Grande, Brazil
Keywords:
Metamodels, denotational semantics, formal methods and MDA.
Abstract:
Denotational semantics is commonly used to precisely define the meaning of a programming language. This
meaning is given by functions that map syntactic elements to mathematically well defined sets called semantic
algebra. Models in semantic algebra need to be processed through reductions towards a normal-form in order
to allow the verification of semantics properties. MDA is a current trend that shifts the focus and effort from
implementation to models, metamodels and transformations during the development process. In order to put
forward denotational semantics in the MDA vision, we turn semantic algebra into an useful domain-specific
language. In this context, this paper describes our proposed MOF metamodel and ATL reductions between
the generated models. The metamodel serves as abstract syntax for semantic algebra. It is useful for static
semantics verifications. The reductions enable processing towards a normal-form to compare semantics. This
process can be guided by using some rewrite system.
1 INTRODUCTION
Metamodels play an important role in the Model-
Driven Architecture (MDA) (OMG, 2007) providing
a way to unambiguously define languages. Each Do-
main Specific Language (DSL) can be associated to a
different metamodel. A metamodel defines the con-
structs of the DSL in the modeling process. Thus, a
model is an instance of these constructs. Metamod-
els are also used to define model transformation, a
technique to transform one source model into a tar-
get model. Transformations play a key role in the
MDA approach, allowing the transformation of the
constructed model into something executable.
The formal semantics of a programmingor model-
ing language is the assignment of meanings to the sen-
tences or components given by a mathematical model
that describes every possible computation in the lan-
guage. Denotational semantics is an useful approach
for precisely defining the meaning of a programming
language (Schmidt, 1986). It is a mapping between a
program and its meaning, called denotation. The de-
notation is a mathematical value, such as a number or
a function. This mapping of the denotational style is
feasible only if the formal notation is algebraic. The
most used algebraic notation is named semantic al-
gebra. A semantic algebra is a formalism for intro-
ducing domains and operations, being considered an
abstract data type.
Simplifying or evaluating semantic models means
reducing its expressions until no more reduction rules
can be applied. A reduction rule receives as input a
semantic model and returns as output another seman-
tic model with some different feature. These reduc-
tions need to be applied in order to compare it with
the meaning of other programs or formalisms.
The MDA architecture does not provide formal in-
frastructure and primitives for the definition of arti-
facts able to represent the required semantic correct-
ness (Kleppe and Warmer, 2003). It deals only with
the definition and manipulationof structural elements,
related to the syntax defined by metamodels. It is ex-
pected that transformations involving programming
and modeling languages as input and output models
should have a conformance relation between models.
The lack of formalization makes the production of
tools difficult because semantics carries the meaning
that is essential to enable automation.
In this paper we propose introducing semantic al-
gebra in the MDA infrastructure. In order to achieve
this goal, a metamodel for semantic algebra and im-
plementation of reductions between the generated
models are suggested. Both are important in the MDA
vision because they: (i) give an abstract syntax to
330
E. S. Barbosa P., Ramalho F., C. A. de Figueiredo J. and D. dos S. Junior A. (2008).
INCORPORATING SEMANTIC ALGEBRA IN THE MDA FRAMEWORK.
In Proceedings of the Third International Conference on Software and Data Technologies, pages 330-336
DOI: 10.5220/0001899703300336
Copyright
c
SciTePress

apply semantic algebra as a DSL; (ii) provide inter-
operability between semantic specifications of many
languages, enabling processing of the denotations;
(iii) enable formal refinement of the involved models,
which can be applied both in endogenous and exoge-
nous transformations (Czarnecki and Helsen, 2003);
and (iv) are important pieces in an ongoing frame-
work for semantic preserving in MDA transforma-
tions having as basis the well-founded theory of De-
notational Semantics.
The paper is structured as follows. Section 2
presents the semantic concepts necessary to under-
stand the proposed work. Section 3 describes the se-
mantic algebra metamodel. Section 4 analyzes the
implementation of reductions between models in this
formalism. Section 5 gives an example of the meta-
model instantiation. Section 6 discusses some similar
works. Section 7 concludes the paper.
2 DENOTATIONAL SEMANTICS
AND SEMANTIC ALGEBRA
The framework of denotational semantics, provided
by Scott and Strachey (Scott and Strachey, 1971), pro-
vides a proper mathematical foundation for reason-
ing about programs and programming languages. It
is based on denotations, that are typically a function
with arguments that represent expressions before and
after execution. They are defined inductively, using
λ-Calculus (B¨ohm, 1975) to specify how the denota-
tions of components are combined.
To give the semantics of a language, a collection
of meanings is necessary. The most used framework
is Domain Theory, which employs structured sets,
called domains, and their operations as data structures
for semantics. Domains plus the operations constitute
a semantic algebra. According to Schmidt (Schmidt,
1986), the semantic algebra:
• clearly states the structure of a domain and how
elements are used by the functions.
• modularizes and provides reuse of semantic defi-
nitions.
• makes analysis easier.
As an example, we chose a subset of the speci-
fication of an imperative programming language ex-
tracted from (Schmidt, 1986). It will also be dis-
cussed and instantiated in Section 5. This semantic al-
gebra has four domains: (I) the Truth Values domain,
corresponding to the boolean type and has true and
false as atomic values and not as operation; (II) the
known Natural Numbers domain, their uncountable
elements and the basic operations plus and equals;
(III) the Identifiers domain, commonly employed as
specific memory addresses, being a set with no op-
erations; and (IV) the Store domain, that models a
computer store as a mapping from identifiers of the
languages to their values. The operations over the
store include: (i) newstore for creating a new store;
(ii) access for accessing a store, and (iii) update for
placing a new value into a store. This is the model-
ing of the classical concept of memory manipulation,
always present in imperative languages.
I. Truth Values III. Identifiers
Domain t ∈ Tr = B Domain i ∈ Id = Identifier
Operations IV. Store
true, false: Tr Domain s ∈ Store = Id → Nat
not: Tr → Tr Operations
II. Natural Numbers newstore: Store
Domain n ∈ Nat = N newstore = λi.zero
Operations access: Id → Store → Nat
zero, one,...:Nat access = λiλs.s(i)
plus: Nat × Nat → Nat update: Id → Nat → Store → Store
equals: Nat × Nat → Tr update = λiλnλs.[i7→n]s
3 THE SEMANTIC ALGEBRA
METAMODEL
We propose a metamodel as the abstract syntax for
the definition of a semantic algebra. Due to space
restrictions, aspects of the metamodel were summa-
rized. The diagram in Fig. 1 shows six MOF packages
covering concepts and relationships in this domain.
The core package represents the identification of
a semantic algebra, and how it is composed by sev-
eral domains. The metaDomains package represents
existing sets or structures which are used as basis
for defining the semantic algebras. The semantic-
Domains package represents a set of elements shar-
ing common properties. Domains may be nothing
more than sets, lattices or topologies. Accompany-
ing a domain we have a set of operations that can
be considered functions. The lambdaCalculus pack-
age represents the λ-Calculus computational formal-
ism which is responsible for function specifications.
The enrichedLambdaCalculus package represents the
inclusion of extra constructs, such as a superset, orig-
inating the enriched lambda calculus. It is provided
through the merge operator because any expression in
the λ-Calculus is also an expression in the enriched λ-
Calculus syntax. The abstractions package contains
specific abstractions identified in several parts of the
metamodel.
The core package is responsible for capturing the
beginning of the denotational specification. The se-
mantic algebra concept is represented by the meta-
INCORPORATING SEMANTIC ALGEBRA IN THE MDA FRAMEWORK
331

Figure 1: Semantic Algebra metamodel.
class SemanticAlgebra composed by zero or many
Domains as represented in Fig. 2. This metaclass
belongs to the semanticDomains package and is de-
scribed in the next subsection.
Figure 2: The core package.
These domains (semantic domains) are sets that
are used as value spaces in programming language
semantics. They are presented in Fig. 3. They be-
long to the semanticDomains package where are de-
scribed with an underlying mathematical set (e.g. nat-
ural numbers, truth values or any other domain) which
provides the isomorphism to an existing well-defined
theory. This information is stored in the Description
metaclass and in its relationship to a MetaDomain.
A semantic domain should be represented as a set
and they can be classified according to its composition
as:
• Primitive Domains: represented by the Primi-
tiveDomain metaclass. Its elements are atomic
and are used as answers or semantic outputs.
This kind of domain is specialized as Character-
Strings, TruthValues, NaturalNumbers, Identifiers
and Unit only. It is incomplete because according
to the described language and its paradigm, addi-
tional domains should be necessary.
• Compound Domains: represented by the Com-
poundDomain metaclass. It enables the cre-
ation of new domains from existing ones, using
some domain building constructions in the Do-
main Theory. There are a number of assem-
bling and disassembling operations of the com-
pound domain. The previously defined domains
are products, disjoint unions, functions and lift, a
type of empty domain.
• Recursive Domains: represented by the Recur-
siveDomain metaclass. It occurs when certain
programming languages features require domains
whose structure is defined in terms of themselves.
A recursive domain is composed by, at least, an-
other domain that can be considered the base case
of the recursion.
Since λ-Calculus is a language with a well-defined
EBNF grammar, we mapped its rules to the lambda-
Calculus package represented in Fig. 4. It has four
kinds of expressions:
• Variables: represent the storage of some concept
to be manipulated in the program.
• Constants: represent an extension of a suit-
able collection of built-in functions, including
arithmetic functions, constants, logical functions,
character constants and more.
• Applications: represent the denotation: the func-
tion f applied to the argument x. It is used as f
x. In the metamodel those expressions are rep-
resented by the roles operator and operand. This
format is known as currying and allows us to think
of all functions as having a single argument.
• Lambda Abstractions: represent constructs to de-
note new functions. A λ-abstraction is a particular
sort of expression which denotes a function. It is
composed by a variable followed by the body of
the function.
These expressions are represented as metaclasses
and grammar constraints are, for instance, relation-
ships between metaclasses. It is enough to represent
compositionality demanded by recursive definitions.
In order to turn the operation specification into a
more suitable task, the syntax of the λ-Calculus is
improved with operators closer to the functional con-
structs. These enriched constructors are metamodeled
in the enrichedLambdaCalculus package in Fig. 5. It
is a superset of the λ-Calculus so that any expression
in the λ-Calculus is also an expression in it.
In this case, Constant and Variable are now gen-
eralized into Pattern because of some inserted opera-
tions that treat both similarly. In addition, some ex-
tra constructs are provided, such as let, case and the
considered infix operator fat bar. Now, a LambdaAb-
straction receives as parameter a pattern, allowing
the pattern matching concept, always present in func-
tional languages. The Let metaclass is composed by
ICSOFT 2008 - International Conference on Software and Data Technologies
332

Figure 3: The semanticDomains package.
Figure 4: The lambdaCalculus package.
Figure 5: The enrichedLambdaCalculus package.
a Pattern instance that is currently instantiated and an
Expression in which this instance will be employed.
The case expression consists of a variable in which
the test will happens and several PatternMatching in-
stances.
4 LAMBDA REDUCTIONS
Evaluating a λ-expression is called reduction. Reduc-
tions are useful for the processing of models towards
a normal-form in order to compare semantics. As λ-
Calculus is inserted in the semantic algebra format,
we followed the same definition. The basic idea in-
volves substituting expressions for free variables in a
similar way that parameters are passed as arguments
in a function call.
In the MDA framework, we employ these reduc-
tions as refinement rules of the semantic models (in-
stances of the semantic algebra metamodel) associ-
ated with each input and output model. These rules
are applied until a normal-form is reached for each
model, on which semantic properties will be veri-
fied. Therefore, these reductions will promote verify-
INCORPORATING SEMANTIC ALGEBRA IN THE MDA FRAMEWORK
333

ing if the MDA transformations are in fact semantic-
preserving. We have chosen to introduce reductions
in MDA by using model transformations. In partic-
ular, for each reduction, we have specified an ATL
module containing minor reductions specified as ATL
rules. In essence, they are rewrite rules that match
input models patterns, expressed as semantic algebra
elements on the input metamodel, and produce output
as semantic algebra patterns.
Our set of ATL transformation rules generates in-
termediate and final representations of semantic alge-
bra specifications. We have implemented the main λ-
reductions described in (Schmidt, 1986): α, β and η.
The reductions were implemented as ATL rules, using
ATL helpers for auxiliary functions or attributes. Due
to the lack of space, we illustrate the β-reduction. It is
useful for simplifying an expression, defining the idea
of evaluation of a function application (f x).
In the module BetaReduction, the formula in
which the β-transformation will be carried out is
(λv.E) e. The input expression needs to be an applica-
tion with the operator as an abstraction, as indicated
at lines 4-5 by the input match. This is necessary to
satisfy the β equation: (λv. E ) E1 ⇒β E[v → E1].
The rule (Abs2AbsFree) at lines 8-10 deals with the
input as a LambdaAbstraction. It invokes an auxiliary
function (line 10) to discover the free occurrences of
the formal parameter in the body of f which are to be
replaced for. The auxiliary function is implemented
with the ATL helper isFree at lines 11-15, which de-
clares that the parameter variable is free, considering
the body of the function as an expression, if: (i) it is
a variable with the same name of the parameter vari-
able; or (ii) it is an application and recursively the
variable is free for the operator or the operand, or (iii)
it is an abstraction with the same parameter and has a
free body.
1: module BetaReduction;
2: create OUT : LC from IN : LC;
...
3: rule Expression2Expression {
4: from
5: in:LC!Expression(in.isApp() and in.operator.isAbs())
6: to
7: out:LC!Expression
...
8: rule Abs2AbsFree {
9: from
10: in:LC!LambdaAbstraction(not(self.isFree(self.v,in)))
...
11: helper def: isFree (v:LC!Variable, e:LC!Expression):Boolean =
12: (e.isVar() and (v.name = e.name)) or
13: (e.isApp() and self.isFree(v,e.operator) or
14: self.isFree(v,e.operand)) or (e.isAbs() and
15: (not(v.name = e.parameter.name) and self.isFree(v,e.body)));
In order to build and validate our approach, we
have adopted the ATL-DT (AI0, 2004) framework.
It is an Eclipse plugin that allows in an integrated
way: (i) specifying and validating metamodels; (ii)
creating and validating models in conformance with
their provided metamodels; (iii) specifying and exe-
cuting model transformations based on metamodels
and applied to valid models. These transformations
are already being applied to several complex seman-
tic models. By adopting a framework that fully sup-
ports most of the OMG standards, we promote the in-
tegration of our work with other existing tools, such
as model or code editors.
5 AN INSTANTIATION EXAMPLE
In order to validate the proposed metamodel, we
reused several classical specifications from (Schmidt,
1986). In Fig. 6 we illustrate the specification for
imperative languages given in Section 2. The intro-
duced labeled boxes represent instantiations of the
metaclasses and the dotted arrows represent instanti-
ations outgoing from the box and ingoing the meta-
classes. First of all, one instance of the metaclass
SemanticAlgebra is shown in the box 1 and four in-
stances of the associated metaclass Domain in the box
2, corresponding to the four existing domains.
In Fig. 7 we give a general view of the instantiated
elements. We deal with three existing primitive do-
mains: TruthValues, NaturalNumbers and Identifiers
instantiated in box 3. We also have one compound
domain: Store, in box 4. Its operations are shown in
the top of box 5, except for Identifiers which have no
operation. It was also necessary to add to the hierar-
chy of the CompoundDomain a new subclass to rep-
resent Store. It was instantiated as a map from Iden-
tifier to a NaturalNumber (the two domains that to-
gether compose the store), implementing a Function-
Space. A domain is also composed by a Description
as shown in box 6. It applies the set of Natural num-
bers from mathematics into the NaturalNumbers do-
main, the commonly used Boolean values from pro-
gramming languages into TruthValues and a set of
identifiers composed by any character string into the
Identifiers domain.
The remaining expressions proposed in the Store
domain operations are instantiated as shown in Fig. 8.
In box 7 we have two nested λ-expressions delimited
by the λ symbol until the end. The first lambda ab-
straction receives the variable i as parameter and has
the second lambda abstraction as expression. The sec-
ond lambda abstraction receives the variable s as pa-
rameter and makes the function application of s onto i
as its expression. The expression in box 8 follows the
same idea, but the expression of a lambda abstraction
is a constant, zero in this case. Box 9 presents the cre-
ation of an anonymous lambda abstraction, with the
variable i as parameter, the variable n as expression
and the anonymous function is applied to the variable
ICSOFT 2008 - International Conference on Software and Data Technologies
334
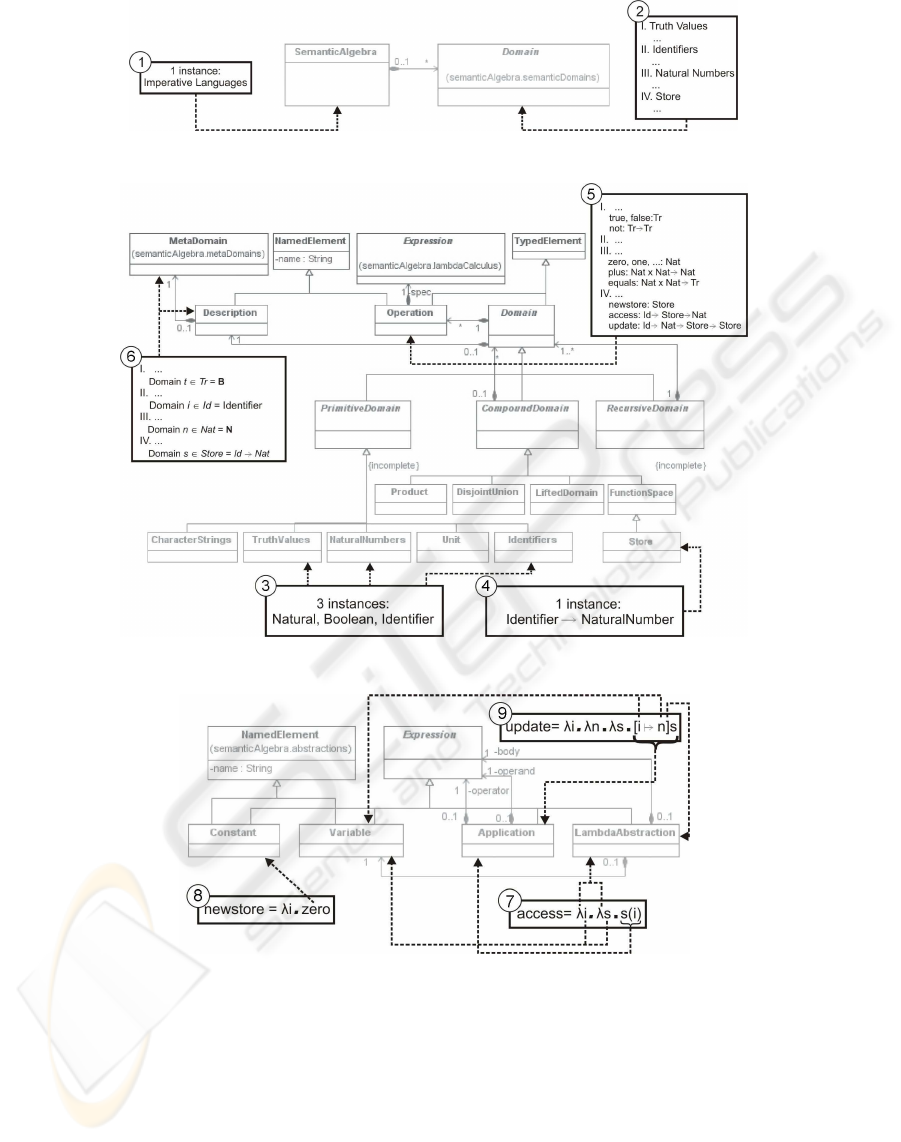
Figure 6: Instantiating the semantic algebra for imperative languages.
Figure 7: Instantiated elements in the semantic domains.
Figure 8: Three specifications built on the λ-calculus formalism.
s concluding the specification.
6 RELATED WORKS
There exists some proposed semantic metamodels in
the context of formal semantics. However, no one fo-
cuses on the semantic algebra of the denotational for-
malism. Kent et al. (Kent et al., 1999) redefines meta-
models for UML/OCL in order to incorporate formal
semantics. In this case, the denotational approach is
realized by redefining: (i) the semantic metamodel for
the language of models (classes, roles, models); (ii)
the semantic metamodel for the language of instances
(objects, links); and (iii) the mapping between these
two languages as semantic equations. However this
work differs from ours because it suffers of the lack
of formalization of the languages in the domain and
codomain. The mapping is not enough to ensure con-
formance between models and makes hard to consider
INCORPORATING SEMANTIC ALGEBRA IN THE MDA FRAMEWORK
335

extensions for dynamic aspects of behavior.
Concerning model transformations, Dominguez
et al. (Dominguez et al., ) investigate the explicit
correspondence between metamodels and ontologies
of different languages. They consider refinement of
metamodels instead of models, as we do here. By
constructing a chain of metamodels, according to
some refinement laws, they analyze refinements in
both sides until that some convergence can be found
to compare meanings. The proposed idea can help to
delimit the difficulties in assuring that semantics are
preserved in some translation but has the limitation
of dealing with the language level, which requires a
high-level of expertise.
7 CONCLUSIONS AND FUTURE
WORK
We proposed a MOF metamodel for semantic alge-
bra and implementation of its corresponding reduc-
tions. The former formally introduces domains and
operations of programming languages, and the later
simplify models towards a normal-form. They play
an important role in the MDA framework because
they: (i) put forward semantic algebra in the MDA
vision, allowing specifications from or to this formal-
ism; (ii) put forward semantic algebra as a DSL al-
lowing formal semantic applications; (iii) enables rea-
soning about meaning and behavior in order to get a
formal conformance between models by using reduc-
tions after transformations; and (iv) have potential to
emerge as crucial elements in the MDA framework in
order to allow semantic preservation in model trans-
formations.
The proposed metamodel and reductions are part
of an ongoing project whose main goal is to guarantee
semantic preservation in model transformations in the
MDA infrastructure. To that effect, the widely rec-
ognized potential of semantic algebra as a semantic
notation for syntactic constructs of programming lan-
guages put its metamodel as a crucial element in the
puzzle of MDA artifacts.
Although QVT is the current OMG’s proposal for
specifying transformations in the MDA vision, we
have adopted ATL. The main reason for this choice
is that QVT tools still have low robustness and its use
is not widely disseminated. On the other hand, ATL is
employed by an increasing and enthusiast community,
with full support to model operations, where, in an
integrated way, one can specify and instantiate meta-
models as well as specifying and executing transfor-
mations on them.
As future work, we intend to propose an extension
on the MDA four-layer architecture in order to in-
clude the semantic algebra metamodel as required ele-
ment for guaranteeing semantic preservation in model
transformations. The reductions will be inferred and
performed automatically by the use of rewriting logic
in rewrite systems.
REFERENCES
(2004). ADT: Eclipse development tools for ATL.
B¨ohm, C., editor (1975). Lambda-Calculus and Computer
Science Theory, volume 37 of Lecture Notes in Com-
puter Science. Springer.
Czarnecki, K. and Helsen, S. (2003). Classification of
model transformation approaches. In Proceedings
of the 2nd OOPSLA Workshop On Generative Tech-
niques in the Context of the Model Driven Architec-
ture.
Dominguez, E., Rubio, A., and Zapata, M. Mapping models
between different modeling languages. In Workshop
on Integration and. Transformation of UML Models,
2002, pages 18–22.
Kent, S., Gaito, S., and Ross, N. (1999). A meta-model se-
mantics for structural constraints in UML. In Kilov,
H., Rumpe, B., and Simmonds, I., editors, Behavioral
specifications for businesses and systems, chapter 9,
pages 123–141. Kluwer Academic Publishers, Nor-
well, MA.
Kleppe, A. and Warmer, J. (2003). Do mda transformations
preserve meaning? an investigation into preserving
semantics. In International Workshop on Metamod-
elling for MDA.
OMG (2007). Model driven architecture.
http://www.omg.org/mda/.
Schmidt, D. A. (1986). Denotational semantics: a method-
ology for language development. William C. Brown
Publishers, Dubuque, IA, USA.
Scott, D. and Strachey, C. (1971). Towards a mathemat-
ical semantics for computer languages. In Proceed-
ings of the Symposium on Computers and Automata,
volume 21 of Microwave Research Institute Symposia
Series.
ICSOFT 2008 - International Conference on Software and Data Technologies
336
