
AN OPTIMIZATION METHOD FOR REDEMPTION AND DUE
DATE MATCHING IN ASSIGNMENT OF ELECTRONIC
RECEIVABLES BY USING INTEGER LINEAR PROGRAMMING
Toshiyuki Moritsu
Systems Development Laboratory, Hitachi Ltd. 890, Kashimada, Saiwai-ku, Kawasaki, Kanagawa 212–8567, Japan
Norihisa Komoda
Graduate School of Information Science and Technologies, Osaka University 2–1
Yamadaoka, Suita, Osaka 565-0871, Japan
Keywords:
Electronic Receivables, Integer Linear Programming, Finance, Due Date Matching, Optimization.
Abstract:
This paper shows an optimization method for redemption and due date matching which assigns the receiv-
ables to the payments date under the pre-defined constraints which related companies specified. Our proposed
method determines the pairs of the receivables and the payment with proper new settlement date which closes
the fluid assets of companies to their target amounts by extending/shortening the redemption/due date. This pa-
per shows that this matching program is categorized in integer linear programming. By applying this matching
mechanism, transferors could utilize credit of issuers and also reduce fluid assets for payments. Effectiveness
of our optimization method is shown by executing simulation which emulates the issuing and receiving status
of receivables in Japanese companies.
1 INTRODUCTION
In recent years, various countries have made progress
in the development of systems for handling credit
transactions electronically, including EBPP/EIPP
(Electronic Bill/Invoice Presentation and Payment) in
the United States (Fairchild, 2003) and e-billing sys-
tems in South Korea (KFTC, 2002). Japan is now also
expecting an increase in this type of business, and in
June 2007 the Japanese parliament approvedthe Elec-
tronically Receivables Legislation (FSA, 2005) which
is due to go into force at the end of 2008. Electron-
ically receivables are a new form of credit whereby
electronic registrations at organizations that register
electronic receivables become only requirement for
the generation and transfer of credit, and are expected
to utilized as a means for the exchange of nominative
claims and credits to payment on which contract doc-
uments and printed bonds are based (Ikeda, 2006).
The assignment of claims allocated to the payment
of electronic receivables owned by a business has the
merit of allowing the transferor to utilize the remit-
ter’s credit rating (Oogaki, 2006). Specifically, when
the transferor (company B) owns electronic receiv-
ables issued by a issuer (company A), even if com-
pany B has a poor credit rating and the electronic
receivables issued by company B have not been re-
ceived by the transferee (company C), then if we sup-
pose that company A has a high credit rating then
company B can pay by transferring credit issued by
company A. This supplementation of reliability by a
third party is particularly useful as a way of utilizing
the credit rating of a parent company in the financing
of subcontractor corporations in business affiliations
that account for approximately 60% of such arrange-
ments in Japan (JSBRI, 2007).
However, it has been pointed out that previous
nominative claims and credits to payment are limited
in terms of the opportunities for utilizing one’s credit
in the assignment of claims. One possible reason for
this is that the payment conditions (amount payable
and due date) and credit redemption conditions are
not exactly same. Since electronic receivables make
it easy to rewrite the conditions electronically, it is rel-
atively simple to accommodate differences in sums by
splitting the electronic receivables. This has actually
been implemented in the book entry transfer system
for short term corporate bonds in Japan. On the other
hand, in cases where the due dates do not match, it is
necessary to adjust the gains and losses of the inter-
349
Moritsu T. and Komoda N. (2008).
AN OPTIMIZATION METHOD FOR REDEMPTION AND DUE DATE MATCHING IN ASSIGNMENT OF ELECTRONIC RECEIVABLES BY USING
INTEGER LINEAR PROGRAMMING.
In Proceedings of the International Conference on e-Business, pages 349-356
DOI: 10.5220/0001905603490356
Copyright
c
SciTePress

ested parties (issuer, transferor, transferee) before al-
tering the conditions. This due date modification has
the side benefits of allowing businesses to make effec-
tive use of surplus floating assets (referred to simply
as “assets” in the following) and providing a means
for supplementing shortfalls in assets. It is thus nec-
essary to reach an agreement on items such as what
the interest rate should be and by how much the term
should be extended or contracted.
It is difficult to make an agreement between the
interested parties regarding the change in due date by
executing work flow between them because it can take
much time to reach an agreement if consideration is
given to factors such as changes of circumstances re-
sulting from conflicting conditions.
Therefore in this study it is envisaged that making
alterations to the due date of electronic receivables in
an effective manner requires a mechanism whereby
the participants first register assets fluctuation targets
and variation conditions whereby changes in due date
can be tolerated, and then combinations of payments
and electronic receivables are determined to satisfy
these constraints. For this study we therefore propose
a matching scheme that optimizes combinations of
payments and electronic receivables so as to achieve
the best possible assets fluctuation targets for all par-
ticipants. In particular, in this matching of electronic
receivables and payments, the level of assets target
achievement of the participants depends not only on
which electronic receivablesshould be combined with
which payments, but also on how the new due date for
the redemption/payment of electronic receivables and
payments is set and matched. We therefore formula-
rize the issue of combining electronic receivables and
payments by including the selection of a new due date
whose selection range is determined by these combi-
nations, and the results can be treated as a problem
of integer linear programming. Also, by simulating
the transaction of electronic receivables under condi-
tions simulating the issue of corporate bills and ac-
counts receivable in Japan, we first verify the extent
to which the assignment of claim is promoted by the
due date matching function. We also verify the opti-
mization effects by comparing the optimized match-
ing of electronic receivables and payments with some
other combination methods.
2 METHOD FOR MATCHING
THE DUE DATES OF
ELECTRONIC RECEIVABLES
In this section we discuss a method for matching elec-
tronic receivables and payments based on the prior
registration of due date alteration conditions which is
a premise of this study. The processing flow is illus-
trated in Fig. 1. First, the participants register their re-
spective asset fluctuation targets and due date adjust-
ment criteria (1). The payment registrations are then
accepted (2), the combination of electronic receiv-
ables and payments is determined based on these in-
formation (3), and approval is obtained for the match-
ing results. The due date adjustment criteria are as-
sumed to consist of a range of possible due dates for
redemption payments, and interest conditions. In the
following, we will discuss the asset fluctuation targets
specified by the participants, the possible range of re-
demption/payment due dates, and the interest condi-
tions.
• Asset Fluctuation Targets.
Each participant specifies when and how much
they would like the current assets to fluctuate. For
example, the estimation of future changes in cur-
rent assets is prepared from predictionsof the pay-
ment and receipt of electronic receivables (and
other settlements), and by setting the target hold-
ings of current assets at each future timing, the
fluctuation targets are set according to the differ-
ence between the target holdings and estimated
transitions.
• Possible Range of Redemption/Payment due
Dates.
If necessary, the participants specify a range for
the extension or contraction of payment due dates
and/or redemption due dates.
• Interest Conditions.
The participants specify a lower limit of interest
to be accepted in cases where the redemption due
date is extended or the payment period is reduced,
and converselyan upper limit of interest to be paid
in cases where the redemption due date is brought
forward or the payment due date is extended. Note
that the interest is set according to the debtor’s
credit rating.
ICE-B 2008 - International Conference on e-Business
350

3 FORMULARIZATION OF THE
PROBLEM OF MATCHING
ELECTRONIC RECEIVABLES
AND PAYMENTS
In this section we will devise a formula for the prob-
lem of matching electronic receivables and payments,
and we will show that this problem can be expressed
as a problem in integer linear programming (Schri-
jver, 1986)(Aardal et al., 2005).
The problem of matching electronic receivables
and payments is expressed using the following nota-
tion.
Constants.
R
ijm
. The m-th electronic receivable issued by issuer i and
held by transferor (current holder) j.
D(R
ijm
). Redemption date of electronic receivable R
ijm
DE(R
ijm
). Upper limit of the extension of the redemption
date of electronic receivables R
ijm
set by issuer i
DS(R
ijm
). Upper limit of the reduction of the redemption
date of electronic receivables R
ijm
set by issuer i
V(R
ijm
). Redemption sum of electronic receivable R
ijm
P
jkn
. n-th payment made to transferee k by transferor j
D(P
jkn
). Payment date of payment P
jkn
DE(P
jkn
). Upper limit of the extension of the payment date
of payment P
jkn
set by transferee k
DS(P
jkn
). Upper limit of the reduction of the payment date
of payment P
jkn
set by transferee k
V(P
jkn
). Payment sum of electronic receivable R
ijm
IP(i, R
ijm
, f)/ IR(i, R
ijm
, f). Upper/lower limit of interest
to be paid/received by issuer i in cases where the
redemption date of electronic receivable R
ijm
is ex-
tended/contracted to date f. Issuer i decide the up-
per/lower limit of interest according floating assets
needs.
IP( j, R
ijm
, f)/ IR( j, R
ijm
, f). Upper/lower limit of interest
to be paid/received by transferor j in cases where the
redemption date of electronic receivable R
ijm
is con-
tracted/extended to date f . Transferor j decides the
Figure 1: Process of Due Date Adjustment between Elec-
tronic Receivables and Payments.
upper limit of interest according her/his floating assets
needs and the lower limit according to credit rating of
issuer of R
ijm
and transferors (who transfer R
ijm
before
transferor j).
IP( j, P
jkn
, f)/ IR( j, P
jkn
, f). Upper/lower limit of interest
to be paid/received by transferor j in cases where the
payment date of payment P
jkn
is contracted/extended
to date f. Transferor j decides the upper/lower limit
same as in case of IP( j, R
ijm
, f)/ IR( j, R
ijm
, f).
IP(k, P
jkn
, f)/ IR(k, P
jkn
, f). Upper limit of interest to be
paid/received by transferee k in cases where the pay-
ment date of payment P
jkn
is extended/contracted to
date f. Transferee k decides the upper/lower limit same
as in case of IP( j, R
ijm
, f)/ IR( j, R
ijm
, f).
C
xe
. Fluctuation target sum of current assets of participant
x on date e
Variables.
v(R
ijm
, P
jkn
, f) . Transferred sum whereby electronic re-
ceivable R
ijm
is allocated to payment P
jkn
at a new due
date f
The Objective function of this matching problem
can be expressed as shown in Formula 1.
Objective Function.
Max(Σ
ijkmn f
|D(R
ijm
) − D(P
jkn
)| · v(R
ijm
, P
jkn
, f) (1)
The target of this problem is to make the best pos-
sible effort to ensure that the fluctuation targets of all
participants are satisfied by the fluctuation of current
assets resulting from changes to the due dates of elec-
tronic receivables and payments. To achieve this goal,
it is preferable to mach the combinations of payments
and electronic receivables having longer discrepan-
cies of due dates with the greatest transferred sums,
within the range of the following constraints. As a re-
sult, the target function can be expressed as the sum
total of the values obtained by multiplying the trans-
ferred sums by the discrepancies between the redemp-
tion due dates and payment due dates, and can be ex-
pressed by formula 1.
Meanwhile, the constraint formulae can be
expressed by Formulae 2 through 15 as follows:
Constraint formulae.
v(R
ijm
, P
jkn
, f) ≥ 0 (2)
V(R
ijm
) ≥ Σ
kn f
v(R
ijm
, P
jkn
, f) (3)
V(P
jkn
) ≥ Σ
imf
v(R
ijm
, P
jkn
, f) (4)
C
xe
≥
Σ
jkmn f
v(R
xjm
, P
jkn
, f) +
Σ
ijmn f
v(R
ijm
, P
jxn
, f) (5)
where C
xe
≥ 0 && D(R
xjm
) ≤ e < f &&
f < e ≤ D(P
jxn
)
AN OPTIMIZATION METHOD FOR REDEMPTION AND DUE DATE MATCHING IN ASSIGNMENT OF
ELECTRONIC RECEIVABLES BY USING INTEGER LINEAR PROGRAMMING
351

C
xe
≤
−Σ
jkmn f
v(R
xjm
, P
jkn
, f) −
Σ
ijmn f
v(R
ijm
, P
jxn
, f) (6)
where C
xe
< 0 && f < e ≤ D(R
xjm
) &&
D(P
jxn
) ≤ e < f
v(R
ijm
, P
jkn
, f) = 0 (7)
where ( f ≤ D(R
ijm
) || D(P
jkm
) ≤ f) &&
D(R
ijm
) < D(P
jkm
) (8)
where ( f ≤ D(P
jkm
) || D(R
ijm
) ≤ f) &&
D(P
jkm
) < D(R
xjm
) (9)
where f < DS(R
ijm
) || f > DE(R
ijm
) ||
f < DS(P
jkn
) || f > DE(P
jkn
) (10)
where (IR( j, R
ijm
, f) < IP(i, R
ijm
, f) ||
IR( j, P
jkn
, f) < IP(k, P
jkn
, f)) &&
D(R
ijm
) < D(P
jkm
) (11)
where (IR(i, R
ijm
, f) < IP( j, R
ijm
, f) ||
IR(k, P
jkn
, f) < IP( j, P
jkn
, f)) &&
D(P
jkm
) < D(R
xjm
) (12)
where C
ie
> 0 && f < e ≤ D(R
ijm
) (13)
where C
ie
< 0 && D(R
ijm
) ≤ e < f (14)
where C
ke
> 0 && D(P
jkn
) ≤ e < f (15)
where C
ke
< 0 && f < e ≤ D(R
jkn
) (16)
The constraint formulae consist of the following three
types:
1. Constraints in which the possible range of trans-
ferred sums is predetermined (formulae 2–4)
2. Constraints in which fluctuations of current assets
arising from transfers associated with changes of
due dates are kept within the fluctuation target
(formulae 5–6)
3. Constraints in which the electronic receivables
and payments that can be combined are predeter-
mined (formulae 7–16)
Constraint formula 2 imposes the condition that
the transferred sum must be positive.
Constraint formula 3 imposes the condition that
the sum total of sums transferred when electronic re-
ceivables are transferred in separate parts does not
exceed the sum of the original electronic receivables
(but not necessarily equal since the splitting of elec-
tronic receivables may leave parts that are not suitable
for transfer).
Constraint formula 4 imposes the condition that
the sum total of payments made by the transfer
of electronic receivables does not exceed the total
amount of be paid (but not necessarily equal since
new issues and combinations are made in cases where
the payable sum cannot be fully allocated by the trans-
fer of electronic receivables alone).
Constraint formula 5 shows that when the fluctu-
ation target of the current assets of participant x on
day e is increased, the increase target of participant x
on day e is greater than the sum of the total amount
of electronic receivables drawn by participant x for an
extension astride day e and the total amount of pay-
ments in which participant x is the transferee for a re-
duction astride day e (a participant’s current assets are
increased by the extension of redemption due dates on
electronic receivables drawn by the same participant,
or by the reduction in payment due date of payments
received by the participant).
Constraint formula 6 is the converse of constraint
formula 5, and shows that when the fluctuation target
of the current assets of participant x on day e is de-
creased, the reduction target of participant x on day
e is less than the sum of the total amount of elec-
tronic receivables drawn by participant x for a reduc-
tion astride day e multiplied by the negative value of
the total amount of payments in which participant x is
the transferee for an extension astride day e (a partic-
ipant’s current assets are reduced by the reduction of
redemption due dates on electronic receivables drawn
by the same participant, or by the extension in pay-
ment due date of payments received by the partici-
pant).
Constraint formulae 7–15 define the possible
range of combinations of electronic receivables and
payments. Specifically, the range for which reverse
combinations are not possible is defined as a trans-
ferred amount of 0 in formula 7, and the applicable
ranges are specified by formulae 8–16.
Range 8 and range 9 specify that electronic receiv-
ables and payments cannot be matched unless the new
due date after modification is between the redemp-
tion date of the electronic receivables and the date on
which the payment is due.
Range 10 specifies that electronic receivables and
payments cannot be matched unless the new due date
after modification is within the redemption dates of
the electronic receivables and the possible range of
payment due dates of the payment.
Range 11 specifies that in cases where the redemp-
tion due date of electronic receivables is before the
date on which payment is due, matching of the elec-
tronic receivables and payments is not possible unless
the interest to be paid by the receiver due to extension
of the redemption due date on the electronic receiv-
ables is less than the interest required by the transferor
due to this extension, and the interest paid by the as-
signee due to a reduction in the redemption due date
is smaller than the interest required by the transferor
ICE-B 2008 - International Conference on e-Business
352

due to this reduction.
Range 12 relates to the case where the redemp-
tion due date comes after the date on which the pay-
ment is due, and is the converse of range 11 where the
payer/payee relationships of interest payments by the
debtor, transferor and transferee are reversed.
Range 13 specifies that when there is an increase
in the fluctuation target for current assets on day e,
it is not possible to perform matching with electronic
receivables issued by the issuer involving a change in
the redemption due date so as to reduce the redemp-
tion due date astride day e (a change that depletes cur-
rent assets). Since this means it is possible to exceed
the target if only one of the combinations is agreed
upon, in this formularization the fact that fluctuation
targets cannot be exceeded is added as a premise to
this constraint.
Range 14 relates to the converse of range 13 in
cases where the current formula fluctuation target of
the issuer is reduced.
Ranges 15 and 16 are the same as ranges 13 and
14 where the issuer imposes limits on the redemption
due data by means of restrictions on changes to the
payment due date in transferee k.
With regard to the definition contents of the above
target functions and constant formulae, first, target
function 1 is the maximization of a primary function
with v(R
ijm
, P
jkn
, f) as a variable, and it takes an inte-
ger value. Also, the constraint formulae are all first-
order inequalities that take v(R
ijm
, P
jkn
, f) as a vari-
able. This problem can therefore be classified as an
integer linear programming problem.
4 EVALUATION
The effects of changes in due date and the effects
of optimizing the combinations of electronic receiv-
ables and payments were verified by simulation. This
section discusses the preconditions under which the
simulation was conducted, and then presents the mea-
surement results.
4.1 Preconditions
There is currently no statistical information relating
to the issue of electronic receivables. We therefore
performed the simulation by assuming conditions for
the issue of electronic receivables based on finan-
cial information from Japanese businesses. Table 1
shows the financial information and the conditions
for the issue of electronic receivables assumed in this
simulation. The financial information was sourced
from corporate statistics published by the National
Tax Agency and from settlement trends for 2003 pub-
lished by the Bank of Japan, including the average
sales figures for Japanese corporations, payable liabil-
ities (accounts payable, bills payable), received credit
(accounts receivable, bills receivable), average sum
of bills cleared, and average sum of accounts receiv-
able. The conditions for the issue of electronic receiv-
ables were assumed based on this financial informa-
tion. Specifically, we made assumptions regardingthe
average redemption period of electronic receivables,
the average frequency of issue and the average sum.
The respective calculation formulae are shown below.
• Average redemption period of electronic receiv-
ables = receivable credit / sales × 365
• Average number of electronic receivables issued
= (bills receivable / average sum of bills cleared
+ accounts receivable / average sum of accounts
receivable) / 365
• Average sum of credit = receivable credit / (bills
receivable / average sum of bills cleared + ac-
counts receivable / average sum of accounts re-
ceivable)
In the simulation, the number of companies was
taken to be 260 (one thousandth of the actual num-
ber of businesses), and measurements were performed
by repeating the transactions over two years. In real
situations, not necessarily all the credit is replaced
with electronic receivables, and not necessarily all
the electronic receivables are subject to being trans-
ferred, so the simulation was performed by making a
few changes to the ratio of transferable sums with re-
gard to the credit sums of the electronic receivables
belonging to a business. The simulation environment
parameters were as follows: MPU: Xeon
1
2.8 GHz,
Memory: 3 GByte, Windows XP
2
, JDK 1.6.0 01
01
3
,
LpSolve 5.5.0.10(Berkelaar et al., 2004). In the evalu-
ation results shown in the next section, measurements
were also performed by varying some conditions of
the other parameters (variation in redemption peri-
ods of electronic receivables, variation in frequency
of issue of electronic receivables, variation in mone-
tary value of electronic receivables, number of com-
panies simulated), but the effects of these changes
were smaller than those of the parameters shown in
Table 1 and thus these results are omitted.
1
Xeon is a registered trademark of Intel Corporation.
2
Windows XP is a registered trademark of Microsoft
Corporation.
3
Java is a trademark of Sun Microsystems, Inc.
AN OPTIMIZATION METHOD FOR REDEMPTION AND DUE DATE MATCHING IN ASSIGNMENT OF
ELECTRONIC RECEIVABLES BY USING INTEGER LINEAR PROGRAMMING
353
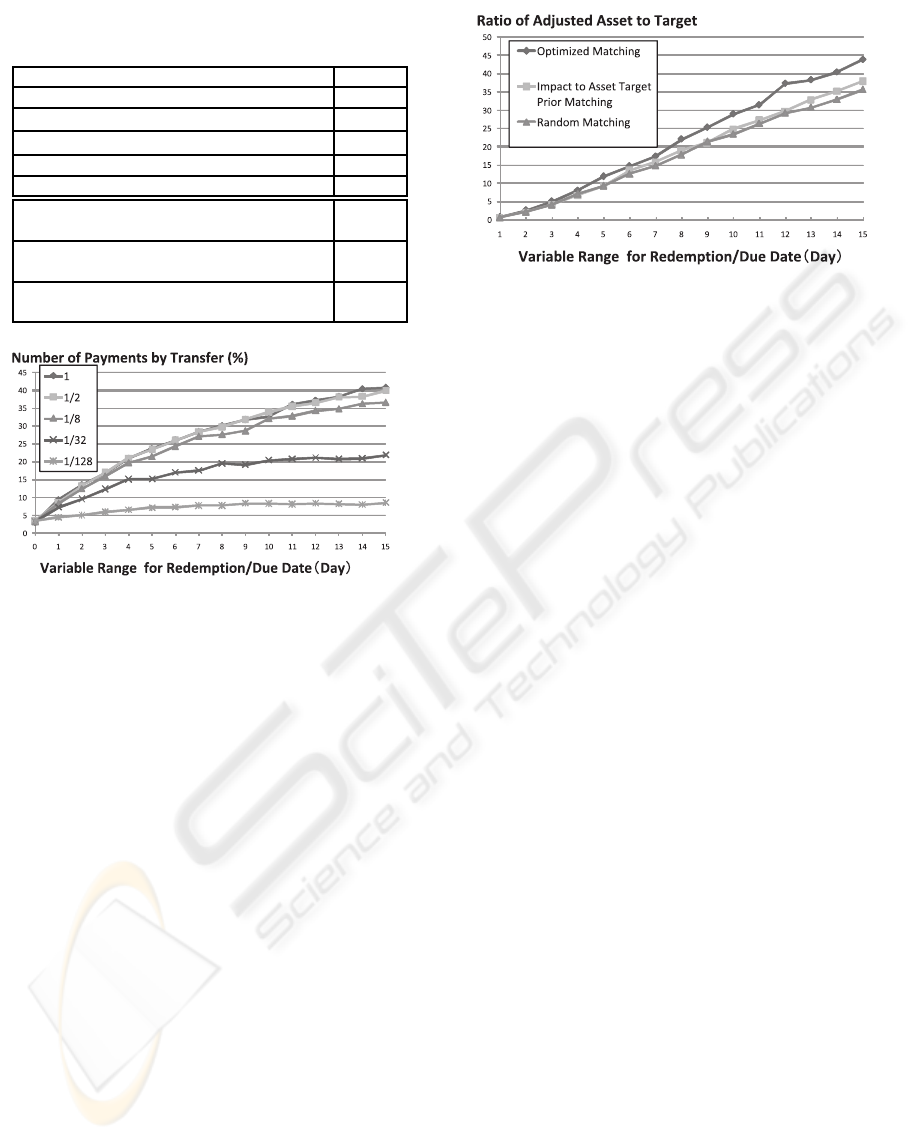
Table 1: Financial Statement of Average Japanese Company
and Assumed Issue Condition of Electronic Receivables.
Total Sales(kY=) 20,483
Total Receivables(kY=) 82,887
⁀
Account Receivables(kY=) 66,287
⁀
Note Receivalbes(kY= 16,600
Average Amount of Account Receivables 2,000
Average Amount of Note Receivables 4,000
Assumed Average Redemption Period 59
of Electronic Receivables(Day)
Assumed Average Issue Cycle of 0.102
Electronic Receivables(Times/Day)
Assumed Average Amount of Electronic 2222
Receivables(kY=)
Figure 2: Ratio of Payments by Transfer.
4.2 Measurement Results
We will first use the due date modification function
to investigate the extent to which payments are pro-
moted by transfers. Next, by optimizing the combi-
nations of payments and electronic receivables, we
will verify the extent to which it is possible to achieve
the participants’ fluctuation targets. Finally, we will
investigate the computational load required for opti-
mization.
The graph in Fig. 2 shows the ratio of all pay-
ments in which payment was made by assignment of
claim. The horizontal axis shows the number of days
by which the payment due date and redemption due
date can be varied in either direction. The multiple
measurement results in this graph correspond to mea-
surements made while varying the criteria regarding
the extent to which the electronic receivables owned
by a business are transferred on a monetary basis.
This evaluation shows the results obtained when the
matching of electronic receivables and payments is
optimized.
In these results, the case where the modifiable date
is 0 corresponds to the case where no changes can be
made to the redemption due date of the electronic re-
ceivables. In this case, the ratio of the payment that
Figure 3: Ratio of Adjusted Asset to Target.
can be assigned in the transfer of electronic receiv-
ables is about 3.3% of the total. On the other hand,
when the redemption due date and payment due date
are set with the ability to be varied forwards or back-
wards by up to 3 days, the ratio of the payment in
the transfer increases to 16.7% (about 5 times larger)
when all the electronic receivables are transferred.
Also, even when the ratio of the electronic receivables
to be transferred is reduced to about 1/32 of the to-
tal electronic receivables, an increase of 12.3% (about
3.7 times) is seen. These results show that by provid-
ing a framework for making adjustments of a few days
in the redemption due date or payment due date, each
business can make a relatively large improvement to
the ratio of payments made by transfers.
The optimization results are shown next. Figure 3
shows the extent to which it is possible to achieve the
fluctuation targets of current assets set by the partici-
pants for each method of matching a number of elec-
tronic receivables and payments. The specific match-
ing methods used to make these measurements were
as follows:
• Randomly ordered Matching.
Matching is performed in random order from
among candidates consisting of electronic receiv-
ables and payments that are capable of being com-
bined.
• Matching in Order of Effects on the Level of
Achievement.
Matching is performed in order of the magnitude
of how the achievement of the fluctuation targets
is affected by candidates consisting of electronic
receivables and payments that are capable of be-
ing combined.
• Matching based on Optimal Pattern Searching.
Matching is performed by searching for optimal
patterns that are closer overall to the fluctuation
targets.
ICE-B 2008 - International Conference on e-Business
354

Figure 4: Effect of Optimization.
Figure 5: Calculation Time for Daily Optimization.
The horizontal axis in the graph of Fig. 3 shows
the number of days by which the payment due date
and redemption due date can be varied in either di-
rection. The vertical axis shows the extent to which
the fluctuation targets preset by each business could
be achieved. With regard to these measurements,
the fluctuation targets of the businesses were set ran-
domly in the range of the sums of electronic receiv-
ables owned by these businesses. Figure 4 compares
the improvement rate of optimization between ran-
dom matching and matching based on the effects on
the level of achievement. These results show that al-
though there is some degree of variation when there
are few modifiable days, the average ratio of improve-
ment is approximately 18.1% for matching based on
the effects on the level of achievement, and approxi-
mately 19.6% for random matching.
Next, the computation time needed to optimize the
combinations of electronic receivables and payments
is investigated using the graph shown in Fig. 5. In this
graph, the number of businesses is shown on the hori-
zontal axis and the time required for the optimization
computations per day is shown on the vertical axis.
In a simulation of 260 companies, the computation
time required for optimization was 113 seconds per
day on average. This remains future work to make
this method in practice because this simulation done
with 1/1000 of actual number of companies and the
computation time glows exponentially according to
increase the number of companies. We discuss this
problem in section 5.
Finally, Table 2 shows the extent to which the
Table 2: Fragmented Number of the Electronic Receivables.
Average Standard Max
Deviation
Random Matching 2.09 1.05 10
Impact to Asset Target 1.38 0.57 7
Prior Matching
Optimized Matching 2.06 1.93 9
electronic receivables are fragmented by the match-
ing of due dates. The number of fragments is a value
that shows on average how many electronic receiv-
ables the original electronic receivables are divided
into at the time of redemption. The average number
of fragments was 2.08 when matching was performed
in random order, 1.38 when matching was performed
in order of the effects on the effects on the level of
target achievement, and 2.06 when matching was per-
formed based on optimal pattern searching. The rea-
son for the small number of fragments obtained when
matching in order of the effects on the effects on the
level of target achievement is thought to be because in
this algorithm, matching is performed preferentially
on groups of electronic receivables and payments in-
volving larger sums and greater differences in due
dates, and these larger sums suppress the fine frag-
mentation of electronic receivables.
5 CONCLUSIONS
In this study, we have proposed a scheme for optimiz-
ing the matching of redemption due dates and pay-
ment due dates for electronic receivables to promote
the transfer of electronic receivables. Specifically,
we have demonstrated an optimization scheme that
makes every effort to make the fluctuations in the cur-
rent assets of each business (caused by changes of due
date) approach their fluctuation targets based on cri-
teria specified by each business regarding the fluctua-
tion targets of current assets, the range of alterations
to due dates, and the rates of interest. We have also
shown that this problem can be classified as a type
of integer linear programming problem. By perform-
ing simulations based on the financial circumstances
of average Japanese businesses, we have shown that
this technique is capable of promoting transfers in-
volving changes of due date and improving the degree
to which fluctuation targets are achieved by optimiza-
tion.
One issue for further study is the problem of elec-
tronic receivables being finely fragmented by the op-
timization process. In the method of this study, if the
fluctuation targets of the participants’ assets are im-
AN OPTIMIZATION METHOD FOR REDEMPTION AND DUE DATE MATCHING IN ASSIGNMENT OF
ELECTRONIC RECEIVABLES BY USING INTEGER LINEAR PROGRAMMING
355

proved, then the electronic receivables can be arbi-
trarily fragmented and a number of payments will be
assigned to a number of new due dates. This fragmen-
tation of electronic receivables leads to increased ad-
ministration costs, so to actually put this method into
practice, it is important to investigate how to control
the fragmentation of electronic receivables.
A second issue is that of partitioning the opti-
mization regions. In this study, optimization was per-
formed by using a single target function to represent
the criteria of all the companies concerned, but this is
inefficient with regard to increasing the scale of busi-
nesses to which the method is applied. In practice,
there is considered to be some degree of locality in
the transaction relationships between businesses, so if
groups of businesses can be split into suitable ranges,
then it should be possible to split the optimization
problem into multiple sub-problems with fewer vari-
ables and constraints. In this way it should be possi-
ble to reduce the computational cost and speed up the
computation time by employing parallel processing.
A third issue is that not necessarily all of the opti-
mal matching results demonstrated by this algorithm
are the best matching results from the viewpoint of
each individual business. For actual operations, an
important issue is therefore to somehow present alter-
native proposals in cases where a business rejects the
matching results.
REFERENCES
Aardal, K., Nemhauser, G., and Weismantel, R. (2005). Op-
timization: Handbooks in Operations Research and
Management Science, volume 12. Elsevier.
Berkelaar, M., Eikland, K., and Notebaert, P. (2004). lp-
Solve: Open Source (Mixed-Integer) Linear Program-
ming System. GNU LGPL (Lesser General Public Li-
cense).
Fairchild, A. (2003). Possible Distinermediation: What
Role for Banks in Electronic Invoicing(EIPP).
In 16th Bled eCommerce Conference eTransfor-
mation, pages 107–118. http://domino.fov.uni-
mb.si/ECOMFrames.nsf/pages/bled2003.
FSA (2005). Summary of Discussion on Electronic
Receivable Legislation from a Financial System
Perspective. Newsletter of Financial Services
Agency, The Japanese Government, pages 2–5.
http://www.fsa.go.jp/en/newsletter.
Ikeda, M. (2006). Electronic receivables - examination
and essay for legislation - (in japanese). Banking
Law Journal, Kinzai Institute for Financial Affairs,
1781:8–19.
JSBRI (2007). White Paper on Small and Medium En-
terprises in Japan. Japan Small Business Research
Institute. http://www.chusho.meti.go.jp/sme
english/
whitepaper/whitepaper.html.
KFTC (2002). Check clearings. KFTC 2002, pages 18–19.
http://www.kftc.or.kr/english/statistics/KFTCAR.pdf.
Oogaki, H. (2006). Finance in secondary loan market
and electronic receivables (in japanese). Banking
Law Journal, Kinzai Institute for Financial Affairs,
1781:20–28.
Schrijver, A. (1986). Theory of Linear and Integer Pro-
gramming. Wiley-Interscience.
Shimamura, A., Moritsu, T., and Someya, H. (2006). Deliv-
ery path length and holding tree minimization method
of securities delivery among the registration agencies
connected as non-tree (in japanese). IEEJ Trans., 126-
C(4):506–512.
ICE-B 2008 - International Conference on e-Business
356
