
ALGORITHM AND AN ELEVATOR CONTROL SYSTEM
EXAMPLE FOR CTL MODEL UPDATE
Laura Florentina Cacovean
Department of Computer Science, Lucian Blaga University of Sibiu, Faculty of Sciences
Str. Dr. Ion Ratiu 5-7, 550012, Sibiu, Romania
Iulian Pah
Department of Sociology, Babes-Bolyai University Cluj-Napoca
Bd. 21 decembrie 1989, no. 120-130, 400604, Cluj-Napoca, Romania
Emil Marin Popa and Cristina Ioana Brumar
Department of Computer Science, Lucian Blaga University of Sibiu, Faculty of Sciences
Str. Dr. Ion Ratiu 5-7, 550012, Sibiu, Romania
Keywords: CTL Kripke model, model update, algorithm, directed graph, implementation.
Abstract: In this paper is presented an update of the Computational Tree Logic (CTL) model checker. The minimal
modifications which appear represent the fundamental concept for model the dynamic system. In the paper
we use five primitive operations discompose from the operation of a CTL update used already by (Baral,
2005) which presented their approach of knowledge updated on the structures of single agent S5 Kripke.
Then we will define the criteria of minimal change for the CTL model update based on these primitive
operations. In the final section of this paper are presented the steps of implement the CTL model updated
and are described some details of algorithm implementation by applying the model update to the elevator
control scenario. The paper (Ding, 2006) is base of results obtained.
1 INTRODUCTION
The verification tools o automated formal, such as
model checkers, shows delivered diagnosis to
provide through automatic error diagnosis in
complex designs, examples in (Wing, 1995). The
current state of the model checkers technique, as
Symbolic Model Verification (SMV) example
(Clarke, 2000), Cadence SMV (McMillan, 2002),
uses SMV as specification language for both CTL
(Computational Tree Logic) and LTL (Lineal
Temporal Logic) model checking. Progressing
update of the method of the model checkers, begun
to employ a formal method for repair approximate
error. Since model, checking can handle verification
problems complex system and as it may,
implemented via fast algorithms, it is quite natural to
consider whether we can develop associated
algorithms so that they can handle system
modification as well. The idea of integrating model
checking and automatic modification has been
investigate in recent years. In work (Harris, 2003)
the model checking is formalized often with an
updating operator satisfied the axioms U1-U8 what
represent the classical proposition knowledge of
updated Katsuno-Mendelzon postulates for belief
update (Baral, 2005). They discussed knowledge
update and its minimal change, based on modal logic
S5. Both the update of the knowledge base and the
knowledge update are currently at the theoretical
research stage. Their approach of knowledge update
could integrate with model checking technology
towards a more general automatic system
modification. In this paper, we considered the
problem of the update of CTL model from both
theories. In substance, as the traditional knowledge
77
Florentina Cacovean L., Pah I., Marin Popa E. and Ioana Brumar C. (2008).
ALGORITHM AND AN ELEVATOR CONTROL SYSTEM EXAMPLE FOR CTL MODEL UPDATE.
In Proceedings of the International Conference on e-Business, pages 77-80
DOI: 10.5220/0001907800770080
Copyright
c
SciTePress

based on the update (Winslett, 1990) consider an
update of CTL model subdue a principle of
minimum inferior change. More, this minimal
change are defined be as well to is definite as a
process based on of some operational processes
which a concrete algorithm for the update of CTL
model could be implemented. In the final section of
this work, we present a study case where we shown
how the system prototype (Ding, 2006) could be
applied for the system modified.
2 SYNTAX AND SEMANTICS
CTL is a branching time temporal logic meaning
that its formulas interpreted over all paths beginning
in a given state of the Kripke structure. A Kripke
model M over AP is a triple M = (S,R,
F
:S
Æ
2
AP
)
where S is a finite set of states, R
⊆
S×S is a
transition relation,
F
:S
Æ
2
AP
is a function that
assigns each state with a set of atomic proposition.
Syntax definition of a CTL model checker (Huth,
2000). A CTL has the following syntax given in
Backus near form: f ::
⊤
|
⊥
|p|(¬f
1
)|f
1
∧
f
2
| f
1
∨
f
2
| f
1
⊂
f
2
| AX f
1
| EX f
1
| AG f
1
| EG f
1
| AF f
1
| EF f
1
|A[f
1
∪
f
2
]|
E[f
1
∪
f
2
] where
p
∈
AP.
A CTL formula is evaluate on a Kripke model M.
A path in M from a state s is an infinite sequence of
states from definition π = [s
0
,s
1
,… , s
i-1
, s
i
, s
i+1
,…]
such that s
0
=s and (s
i
,s
i+1
)
∈
R holds for all i ≥ 0. We
write (s
i
, s
i+1
)
⊆
π and s
i
∈
π. If we express a path as π
=[s
0
,s
1
,…,s
i
,…,s
j
,…] and i<j, we say that s
i
is a state
earlier than s
j
in π as s
i
< s
j
.
Semantics definition of a CTL model checker
(Huth, 2000). Let M = (S,R,
F
:S
Æ
2
AP
) be a Kripke
model for CTL. Given any s in S, we define if a CTL
formula f holds in state s. We denote this by (M,s) ╞
f. The satisfaction relation ╞ define by structural
induction on all fourteen CTL formulas (Ding,
2006). We assume all the five formulas CTL
presented in the contextually as the paths are
satisfied. Be a CTL Kripke model which satisfies the
CTL formulas and we considered as a model that
can be updated satisfying given formulas. The
minimal change should define, based on some
operational process, a concrete algorithm for CTL
model update that can be implemented.
The CTL update definition: Be a CTL Kripke
model M=(S,R,
F
) and a CTL formula f. An update
of M=(M,s
0
), where s
0
∈
S with f is a CTL Kripke
model M' = (S',R',
F
') such that M'= (M',s
0
'),
(M',s
0
')╞ f where s
0
'
∈
S'. We use Upd(M, f) to
denote the result M' and Upd(M,f) =M if M ╞ f.
3 PRIMITIVE OPERATORS
P
1
. Add an only relation. Given M = (S, R, F), its
updated model M' = (S', R', F ') is the result of M
having only added one new relation. That is S'= S,
F '=F, and R' = R∪{(s
add
,s
add2
)} where (s
add
, s
add2
)∉R
for one pair of s
add
,s
add2
∈S.
P
2
. Remove an only relation. Given M = (S, R, F),
its updated model M' = (S', R', F ') is the result of M
having only removed one existing relation. That is,
S'= S, F ' = F, and R' = R-{(s
rem
,s
rem2
)} where (s
rem
,
s
rem2
)∈R for one pair of s
rem
, s
rem2
∈S.
P
3
. Substitute a state and its associated with an only
relations. Given M = (S, R, F), its updated model M'
=(S',R',F ') is the result of M having only substituted
one existing state and its associated relations. That
is, S' = S[s/s
subst
], R' = R∪{(s
i
, s
subst
), (s
subst
,s
j
)|for
some s
i
, s
j
∈S}-(s
i
,s),(s,s
j
)|(s
i
,s),(s,s
j
)∈R} and F '(s) =
F (s) for all s∈S ∩ S' and F '(s
subst
) = τ (s
subst
), where
τ is a truth assignment on s
subst
.
P
4
. Add a state and it associated with an only
relations. Given M = (S, R, F), its updated model M'
= (S',R',F ') is the result of M having only added one
new state and it associated relations. That is, S' =
S∪{s
addst
}, R'=R∪{(s
i
, s
addst
),(s
addst
,s
j
)|s
i
,s
j
∈S∩S'}
and F '(s)=F(s) for all s∈S∩S' and F '(s
addst
)=τ (s
addst
),
where τ is a truth assignment on s
addst
.
P
5
. Remove a state and it associated with an only
relations. Given M = (S,R,F), its updated model M'
= (S',R',F ') is the result of M having only added one
existing state and its associated relations. That is, S'
=S-{s
remst
|s
remst
∈S}, R'=R-{(s
i
, s
remst
),(s
remst
,s
j
) | for
some s
i
,s
j
∈S} and F '(s) = F (s) for all s∈S ∩ S'.
All the changes on CTL model can be in terms of
all five operations. It can be arguing P
3
can be
defined in terms of P
4
and P
5
. Anyway, we treat state
substitution differently from a combination of state
addition and state removed. That is the context,
whenever it substitutes a state needed, applied P
3
directly more than P
4
followed of P
5
. This thing will
simplify definition of minimal change of the CTL
model.
For defined the criteria of minimal change of
ICE-B 2008 - International Conference on e-Business
78
update CTL model, it needs to consider the changes
for both states and relations for the underlying CTL
models. We achieve these specifying the differences
among states and relations on the models CTL using
the primitive operations. Be any two sets X and Y,
symmetrical difference among X and Y be denoted
as Diff(X, Y) = (X - Y)
∪
(Y - X). Be two CTL
models, M = (S, R,
F
), and M' = (S', R’,
F
') for each
primitive operation P
i
with i = 1,…,5, Diff P
i
(M,M')
indicates the differences between one of two the
CTL models where M' is a resulting model from M,
that make clear this difference between this
operations the types may occur. Since P
1
and P
2
only
changes relations, we define DiffP
i
(M,M')=(R - R')
∪
(R'-R) where i = 1, 2. For the operations P
3
, P
4
and P
5
, we define DiffP
i
(M,M')=(S-S')
∪
(S'-S) with
i=3,4,5. Although any state changes caused by P
3
,
P
4
, P
5
will imply also correspondence changes on
relations, we only count the modifications states and
take the state change as the primitive factor in order
to measure difference between and M'. For the
operations P
3
, we should consider the case, which a
state is substitute with a new state. For this is
necessary difference between these two states to be
minimal before the condition of formulated update.
A formal algorithm for the proposed CTL model
update approach is described in (Ding, 2006) and
(Cacovean, 2007).
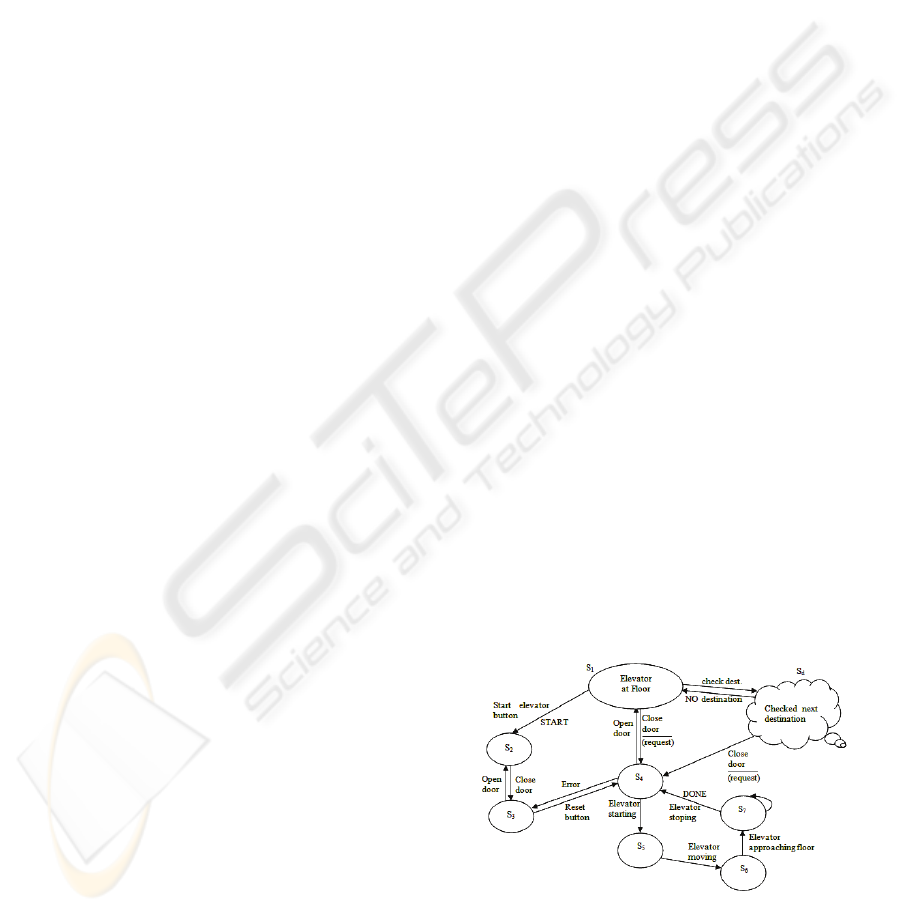
4 ELEVATOR EXAMPLE
In this section we present a study of case where it is
illustrated the features of CTL model updated
approaches.
As example, we shall present a scenario for an
elevator control system. The designer analyzes the
state-transition diagram for the only control
transformation, Elevator Controller (EC), finds eight
locked-state events (Gomma, 1993). These locked-
state events occur because the EC, in most instances,
takes one action and then awaits a response before
moving on a new state. In fact, have only two event
flow, Up and Down Request, when we denote with
Move state when the request exist and is not a
locked-state event. This event flows is not qualify
because each of them can arrive any time a client
presses a floor button or when the scheduler
schedules an elevator. The remaining events can
only arrive when the EC is expecting them.
We assume that we have an elevator system
control which including in first case, a process for
normal moving of lift cabin and in second case, for a
faulty process. In first case for the normal moving
the elevator cabin process don’t appear with errors,
so the door is closed and the passenger going up or
down when the button is pressed. For the second
process, the faulty process appears when the lift
cabin isn’t moving when the button is pressed for
start the moving. The aim of the model is where the
faulty process appears. The objective of model
updating, on other word, is to correct the original
model, which contains the faulty process. Starting
from the original CTL structure for our propose EC
system presented in the figure 1 with eight states
denoted with s
1
, s
2
,…, s
7
, and s
d
state we added for
checking if the elevator is required of another
passenger.
The Kripke model has eight states and the
propositional variables are from the set {Start,
Close, Move, Error}. Start (St) represented the start
button for start moving up or down the elevator,
Close (Cl) represent the close door to the lift cabin,
Move (Mv) is moving up or down the elevator and
Error (Er) means occur some error.
The formal definition of the Kripke structure of
EC is given by M=(S,R,
F
), where S={s
1
,s
2
,…, s
7
},
R={(s
1
,s
2
), (s
2
,s
3
), (s
3
,s
2
), (s
3
,s
4
), (s
4
,s
3
), (s
4
,s
5
),
(s
5
,s
6
), (s
6
,s
7
), (s
7
,s
7
), (s
7
,s
4
), (s
4
,s
1
), (s
1
,s
d
), (s
d
,s
4
),
(s
d
,s
1
)}, AP={St, Cl, Mv, Er}. The
F
assigns state s
1
in M with not start, not close, not move and not
error, write this as
{
¬
St,
¬
Cl,
¬
Mv,
¬
Er}. State
s
2
={St,
¬
Cl,
¬
Mv,Er}, s
3
={St,Cl,
¬
Mv, Er},
s
4
={
¬
St,Cl,
¬
Mv,
¬
Er}, s
5
={St,Cl,
¬
Mv,
¬
Er},
s
6
={St,Cl,Mv,
¬
Er} and s
7
={
¬
St,Cl,Mv,
¬
Er}.
The model shown hereinbefore:
Figure 1: The CTL structure of Elevator Controller.
In figure 1 START represented the start elevator,
Open and Close represent the open door and close
the door, RESET is for a new initialization and
ALGORITHM AND AN ELEVATOR CONTROL SYSTEM EXAMPLE FOR CTL MODEL UPDATE
79

DONE represents the done moving of elevator.
The faulty process from this graph is the path [s
1
,
s
2
,
s
3
,
s
4
]. The interpretation is: start elevator {s
1
,s
2
}.
In the state s
2
we observed that have not close, that
is the door and it isn’t close, and the moving is out
of order and it pointed some error. Passed from the
state s
2
in the state s
3
where the door elevator shall
be close. In the state s
3
has error and the movement
of elevator don’t start so it shall push the reset
button for the reestablishment. That is, from s
3
passed to the state s
4
. Observed that the process with
normal move in the case view from the original CTL
Kripke structure through [s
1
, s
4
, s
5
, s
6
, s
7
]. Noticed
that this model do not satisfies the property f =
¬EF(St∧EG¬Mv) (Harris, 2003). The CTL model
updated brings a minimum modification of the
Kripke model which satisfies the property f. Firstly,
it should analyze f in AG(¬(St∧EG¬Mv)) for
remove the symbol ¬. The translation is doing with
the function Upd¬. Then is necessary to check each
state whether it satisfies ¬(St∧EG ¬Mv). This string
shall be parsing before it is checked. Selecting the
EG¬Mv to elevator through the model checking
function for EG.
In this model, any path has any state when
¬
Mv
is selected. Here are searched the paths in the form
[s
1
,s
2
,s
3
,s
4
,s
1
,…] and [s
1
,s
4
,s
1
,…] which represent the
connected components loops satisfy EG
¬
Mv. Then
are identified all states with St, these are {s
2
,s
3
,s
5
,s
6
}.
Then are selected the states with St and
¬
Mv, these
are {s
2
,s
3
}. Because the AG(¬(St∧EG¬Mv)) formula
identifies the model don’t have the both states St and
¬
Mv, is necessary an execution with states s
2
and s
3
so it should apply the updated model. From
execution of Upd
AG
function, we shown the case in
which applying P
3
on the state s
2
and s
3
. The first
translate will be from ¬(St∧EG¬Mv) to
¬St∧¬EG¬Mv, therefore s
2
and s
3
are updated with
any ¬St or ¬EG¬Mv by the main function CTLUpd
what is dealt with ∨ and with the Upd
¬
function. In
other words, the new states of s
2
and s
3
shall be
denoting with s
2
′ and s
3
′. The Upd
AG
(M,¬(St∧
EG¬Mv)) function calls the main function
CTLUpd(M,
¬
St) or CTLUpd(M, ¬EG¬Mv) for the
case f
1
∨ f
2
. We choose the ¬St because this is
simplest than ¬EG¬Mv. In this case is necessary to
update the St in states s
2
and s
3
of path π with ¬St
instead, then no states on path π have the
specification EF(St∧EG¬Mv). M ′=(M′,s
1
)╞ ¬EF(St
∧ EG ¬Mv). The state s
2
′
is set {¬St,¬Cl, ¬Mv, Er}
and the state s
3
′
is set {¬St,Cl,¬Mv, Er}.
The algorithm will generate one of the three
resulting models without specific indication, because
criteria used are satisfying all the minimally changes
from the original model. We consider that our
elevator model propose is a model much more
simple for understandable and for implemented,
because we used a steps method to illustrate this
elevator controller. In our case we used the CTL
model checker update, verifying all five properties
mentioned above which are accomplished also in our
case of study.
5 CONCLUSIONS
In this paper, we presented a formal approach for the
update the CTL models. Specification of five
primitives on the CTL Kripke models (Ding, 2006),
define the minimal change criteria of the CTL model
updated. Also in this paper are presented semantics
and the computing property of approach that we
used. The proposed case study is an update principle
of minimal change with maximal reachable states,
which can significantly improve the update results in
modification scenarios of complex system.
REFERENCES
Baral C. and Y. Zhang, 2005, “Knowledge updates:
semantics and complexity issues”, Artificial
Intelligence, 164, 209-243.
Cacovean L., Popa E.M., Brumar C.I., 2007,
Implementation of CTL Model Checker Update, in
Proc. 11th WSEAS Int. Conf., COMPUTERS, Greece
Clarke E.Jr., O. Grumberg, and D.A. Peled, 2000, “Model
Checking”, MIT Press, Cambridge
Gomma H., 1993, “Software Design Methods for
Concurrent and Real-Time Systems”, Addision-
Wesley Publishing Company, Reading Massachusetts
Harris H. and M. Ryan, 2003, ”Theoretical foundations of
updating systems”, in Proc. 18th IEEE, 291-298.
Huth M. and M. Ryan, 2000, ”Logic in Computer Science:
Modelling and Reasoning about Systems”, Cambridge
University Press.
McMillan K. and N. Amla, 2002, ”Automatic abstraction
without counterexamples”, in Cadence Berkeley Labs.
Wing J. and M. Vaziri-Farahani, 1995, ”A case study in
model checking software”, in Proc. 3 ACM SIGSOFT.
Winslett M., 1990, ”Updating Logical Databases”,
Cambridge University Press, 1990.
Ding Y., Yan Zhang, 2006, ”CTL Model Update:
Semantics, Computations and Implementation”. ECAI,
Italy.
ICE-B 2008 - International Conference on e-Business
80
