BUSINESS PROCESSES MANAGEMENT USING PROCESS

ALGEBRA AND RELATIONAL DATABASE MODEL

Kelly Rosa Braghetto, Jo

ao Eduardo Ferreira

Department of Computer Science, University of S

ao Paulo, Rua do Mat

ao 1010, 05508-090 S

ao Paulo, Brazil

Calton Pu

College of Computing, Georgia Institute of Technology, Atlantic Drive 801, 30332-0280 Atlanta, U.S.A.

Keywords:

Business Process Management, Workﬂows, Process Algebra, Relational Databases.

Abstract:

Integrating information systems with tools that manage workﬂows and business processes is not always

a simple task. This difﬁculty becomes more accentuated when the execution control assumes countless

business processes. This work presents NavigationPlanTool (NPTool), a tool to control the execution of

business processes that can be easily integrated into the information systems. NPTool is supported by

Navigation Plan Deﬁnition Language (NPDL), a language for business processes speciﬁcation that uses pro-

cess algebra as formal foundation. NPTool implements the NPDL language as a SQL extension and offers

two other important services: processes instantiation and process instances execution monitor. This paper

describes the NPTool showing how the process algebra features combined with a relational database model

can be used to provide a scalable and reliable control in the execution of business processes.

1 INTRODUCTION

Business Processes Management (BPM) involves

methods, techniques and tools to support the project,

the execution, the management and the operational

analysis of business processes (Leymann et al., 2002).

While the traditional deﬁnitions of workﬂow place

emphasis on the execution of operational processes,

BPM also gives support to the diagnosis phase, al-

lowing the processes to be analyzed in order to detect

ﬂaws and possible improvements to the project.

In this context, associating formal frameworks

with the process project phase is valuable since they

provide non-ambiguous models, improve the diagno-

sis capability and enable a reliable execution control

of the process.

Although there are a number of tools based on

formal frameworks directed to the management of

workﬂows and business processes, integrating these

tools with other applications isn’t always easy. Some

of these tools are exclusively developed for mod-

eling and simulation of processes, as occurs in

CPN/Tools (Beaudouin-lafon et al., 2000). In other

cases, the tools effectively carry out the execution

control of business processes, but they do not pro-

vide mechanisms that allow them to be easily used

within the information systems that manage business

processes.

This work presents the NavigationPlanTool

(NPTool), a tool that offers mechanisms for the repre-

sentation and execution control of business processes

supported by a process algebra formalism (Fokkink,

2000). NPTool uses the Navigation Plan Deﬁni-

tion Language (NPDL) (Braghetto et al., 2007) and

a relational database to specify business processes

and to control their instantiations and executions.

NPTool implements NPDL as an extension of SQL;

this implementation allows an easy integration with

traditional information systems, which generally al-

ready have mechanisms that facilitate the access to

RDBMSs. The storage of the processes data in a rela-

tional database adds scalability to the execution con-

trol provided by NPTool. Moreover, the processes

deﬁnitions can be reused in different applications. In

this context, the database maintained by NPTool can

be viewed as a common repository of processes.

Section 2 presents a summary of the related works

and the reasoning behind the use of NPDL. Sec-

tion 3 describes the services offered by the Naviga-

tionPlanTool; in particular, Section 3.1 describes the

323

Rosa Braghetto K., Eduardo Ferreira J. and Pu C. (2008).

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL.

In Proceedings of the International Conference on e-Business, pages 323-333

DOI: 10.5220/0001908903230333

 SciTePress

data structures in the relational database model to

represent the processes, and Section 3.2 explains the

mechanism for execution control. Using a real appli-

cation as example, Section 4 illustrates the execution

control applied to an instance of a process. Finally,

Section 5 discusses the contributions of this work.

2 RELATED WORK

Management technologies for business processes

were developed to meet the following needs: (1) to

promote the separation between the speciﬁcation of

the process and its implementation; and (2) to take

away from the applications the responsibility of the

execution control of business processes. Among the

various existing languages to deﬁne business pro-

cesses, it is not easy to see a formal pattern as a rep-

resentation basis, one that is capable of expressing in

a non-ambiguous way the semantics associated to the

existing constructions in these languages. The for-

malisms regarded as natural candidates for this role

are the Petri nets and the process algebras. Works

such as (Aalst, 1998), (Puhlmann and Weske, 2005)

describe the use of these formalisms in the speciﬁca-

tion of business processes.

The Yet Another Workﬂow Language

(YAWL) (Aalst and Hofstede, 2005) is the most

well succeeded approach for business process speciﬁ-

cation based on Petri nets. It was developed intending

to provide means for deﬁning all the original control-

ﬂow patterns described in (Aalst et al., 2003). Also

with the intention of representing business processes

with a formal basis, Navigation Plan Deﬁnition

Language (NPDL) (Braghetto et al., 2007) was

created. NPDL is based on the concept of navigation

plan of RiverFish architecture (Ferreira et al., 2005)

as well as in the operators of ACP (Fokkink, 2000), a

member of the family of process algebras. The navi-

gation plan was formalized in (Ferreira et al., 2006)

as a set of all business processes demanded from

an application in order to achieve business goals.

Like in processes algebras, processes in NPDL are

deﬁned by algebraic expressions. The expression of

a process is built based on NPDL operators and steps

(atomic actions or processes); the operators indicate

the execution order of the steps. For completeness,

we will provide an overview of NPDL operators.

2.1 NPDL Operators

The basic control-ﬂow patterns described in (Aalst

et al., 2003) can be easily represented with three basic

operators of NPDL:

•Sequential Composition (“.”). the process term

A.B means that the activity B will be enabled for ex-

ecution after the completion of the activity A. An ac-

tivity can be an atomic action or a subprocess;

• Alternative Composition (“+”). the process

term A + B means that initially both activities A and

B will be enabled for execution, but only one of them

can be executed;

• Parallel Composition (“||”). the process term

A||B means that the activities A and B can be executed

parallelly.

These basic operators were directly extracted from

ACP (Algebra of Communicating Processes) and have

their semantics formally deﬁned by a set of transition

rules that will be presented in the Section 3.2. In or-

der to represent all control-ﬂow patterns identiﬁed by

Aalst et al in (Aalst et al., 2003), the NPDL was im-

proved with additional operators:

• Interleaved Parallel Composition (“|∗”). the

process term A|∗B means that the activities A and B

can be executed in any order (e.g., A.B+B.A), but not

in parallel;

• Multi Merge Composition (“&”). the process

term A&B means that the activity B will be enabled

for execution after the completion of each thread of

control of activity A;

•Discriminator Composition (“∧”). the process

term A ∧B means that the activity B will be enabled

for execution after the completion of the ﬁrst thread

of control of activity A;

• Unlimited Repetition (“?∗”). the process term

A?∗ means that the activity A can be executed an un-

restricted number of times;

• Number Limited Repetition (“?n”, where n

is a positive integer number). the process term A?5

means that the activity A must be executed ﬁve times;

•Function Limited Repetition (“? f ”, where f is

a function that returns a positive integer number). the

process term A? f

means that the activity A must be

executed the number of times calculated by function

at execution time;

• Conditional Execution (“%r”, where r is a

rule, e.g. a boolean function). the process term %r

means that the activity A will be enabled for execution

if the return value of the rule r

is true at execution

time;

• Negative Conditional Execution (“%!r”,

where r is a rule, e.g. a boolean function). the process

term %!r

A means that the activity A will be enabled

for execution if the return value of the rule r

is false

at execution time.

Providing more details about NPDL is beyond the

scope of this paper; the deﬁnition of the language

and the speciﬁcation in NPDL of each one of the 20

ICE-B 2008 - International Conference on e-Business

324

control-ﬂow patterns described in (Aalst et al., 2003)

can be seen in (Braghetto et al., 2007).

3 NavigationPlanTool

NavigationPlanTool (NPTool) provides methods for

storing actions and processes in a relational database

and for controlling the instantiation and execution of

these processes. The tool offers operations like cre-

ation/removal of instances and services for monitor-

ing the navigation plan execution. These services are

also responsible for storing logs of the execution of

navigation plans in the database and for recovering

executions that have been interrupted before comple-

tion.

The programming language used in the implemen-

tation of NPTool was Java (Java 2 Platform Standard

Edition - J2SE 5.0). NPTool extends JDBC API -

Java DataBase Conectivity Application Programming

Interface. JDBC enables Java programs to execute

SQL commands and to interact with databases that are

compatible with SQL standard. The usage of JDBC

turns NPTool into a RDBMS independent tool. Since

it was developed as a library of functions, the NPTool

can be easily integrated into other Java applications.

NPTool is composed of three services:

• NPDL Interpreter. receives an input command

and makes the lexical, syntactic and semantical anal-

ysis. There are two possible situations: (1) the com-

mand is a NPDL valid command, and (2) the com-

mand is not a NPDL valid command. In the for-

mer case, the interpreter will translate the command

to pure SQL commands before the submission to the

RDBMS. In the latter case, the command will be

directly passed to the RDBMS. The translated SQL

commands will be executed over a relational database

environment whose tables are created by the inter-

preter to store processes, actions and instances data;

• Process Instantiation Service. provides func-

tions for creating process instances. A process in-

stance represents a request to a speciﬁc process. All

the instance data, as well as process deﬁnition data

associated with the instance, are stored in a database;

• Process Instance Execution Monitor. is re-

sponsible for linking a process instance to its execu-

tion data (navigation plan). This service contains the

functions that control the execution of the navigation

plan of a process instance.

3.1 The Relational Data Structures

Created by NPDL Interpreter

The relational data model does not have appropriate

structures for representing processes and, therefore,

it requires an additional data structure to achieve this

task.

In (Braghetto et al., 2007), the NPDL syntax was

deﬁned as an extension of the SQL syntax. The main

goal of implementing NPDL as a SQL extension was

to enable a RDBMS to create and handle business

processes, providing to information systems an easy

access to these features. The data structure kept stored

in a database by NPTool is represented in the extended

entity-relationship diagram shown in Figure 1. The

diagram shows the data structures needed for repre-

senting business processes and for controlling their

instantiations and executions.

In NPDL, the navigation plan of a process

is deﬁned by an algebraic expression formed by

steps composed by operators that indicate the ex-

ecution order of these steps. The relationship-

set NAVIGATION PLAN REL between the entities-set

PROCESS and STEP represents this deﬁnition. The

specialization of STEP is total and disjoint, i.e., each

entity in STEP is a process, or an action, or an op-

erator, or a rule, or a function or a number. As

described in Section 2.1, rules are always associ-

ated with the operators “%” and “%!”, whereas func-

tions and numbers are associated with operator “?”.

The entity-set PROCESS INSTANCE and the relation-

ship INSTANCE LOG REL are associated with the in-

stantiation and control of process execution. An entity

of PROCESS INSTANCE is always associated with an

entity of PROCESS, as the relationship PROCESS INS-

TANCE REL shows; an instance represents a process

request. The relationship INSTANCE LOG REL repre-

sents the data related to execution status of the steps

that compose the navigation plan of a process in-

stance. Each entity of INSTANCE LOG REL represents

the execution of a step in a speciﬁc process instance.

In Section 3.2, the implementation of the service

Process Instance Execution Monitor will be detailed

to show how process algebra properties and this re-

lational database model were used for developing a

scalable and reliable engine that controls the business

processes execution.

3.2 The Execution Control of Business

Processes in NPTool

When an execution of a process instance is started,

the navigation plan associated with the instance is re-

covered from database. According to the algebraic

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL

325

Figure 1: Extended entity-relationship diagram of process data.

expression that represents the navigation plan, an ex-

pression tree of the instance is built. Expression trees

are used in the execution monitor service to determine

the execution order of the steps in the navigation plan.

In this work, the expression tree of a process instance

was called navigation tree. A navigation tree node can

represent one of these three elements: a NPDL opera-

tor, an action or a process. A navigation tree is a com-

plete binary tree; its internal nodes represent binary

operators of NPDL, whereas its leaf nodes represent

actions or processes. As the navigation tree nodes rep-

resent the possible execution steps, an important at-

tribute of a node is its current status. A node, in a spe-

ciﬁc point of the instance execution, can be in one of

the following states: not started (N), started (S), ﬁn-

ished (F) or canceled (C). The Figure 2 shows an hy-

pothetical example of one of the possible navigation

tree for an instance of process P = (a + b).c.(dke). f .

Figure 2: Navigation tree of an instance of process

P = (a + b).c.(dke). f .

After creating the navigation tree, the execution

monitor recovers the current state of the instance exe-

cution by consulting the execution instances log, that

is stored in the database. This operation only is done

for instances that have already started their execution,

but have not ﬁnished it yet. When an instance execu-

tion is started, all nodes in its navigation tree will have

the current status not started. If the instance execu-

tion have already been started in a previous execution

of the monitor service, there will be records related to

the instance in the log and they must be loaded to the

navigation tree. This is made by updating the status

of the tree nodes associated with the steps indicated as

started, ﬁnished or canceled in the log. Each step per-

formed in the navigation plan of an instance results in

the insertion or update of a record in the log.

−→

√

x + y

−→

√

−→ x

x + y

−→ x

−→

√

x + y

−→

√

−→ y

x + y

−→ y

(1)

−→

√

x.y

−→ y

−→ x

x.y

−→ x

(2)

−→

√

xky

−→ y

−→ x

xky

−→ x

−→

√

xky

−→ x

−→ y

xky

−→ xky

(3)

Figure 3: Transition rules for basic operators of process al-

gebra. The variables x and y in the rules range over basic

process terms, while v ranges over the set of atomic actions.

The “navigation” through the tree of an instance

determines the execution order of the steps of this

instance. The algorithms of the monitor service of

NPTool use the semantics of NPDL operators and the

transition rules of process algebra to visit a naviga-

tion tree. Figure 3(1,2,3) shows the transition rules

extracted from (Fokkink, 2000) that deﬁne the oper-

ational semantics of terms of basic process algebra

and ACP. The operational semantics of a language de-

scribes how a valid sentence must be interpreted in

sequential steps. Figures 4 to 6 show how the transi-

tion rules are applied on the navigation tree branches

to guarantee that the instance status, after starting or

ﬁnishing the execution of an action, will be consistent

with the behavior speciﬁed by the algebraic expres-

sion of the process associated with the instance.

The four rules in Figure 3(1) states that the pro-

cess deﬁned by the term x + y terminates successfully

after executing x or y. Figure 4 shows how the alter-

ICE-B 2008 - International Conference on e-Business

326

Figure 4: State transitions for a branch rooted at an operator

of alternative composition.

native composition operator (“+”) is treated in a nav-

igation tree branch. As in ﬁgures 7 to 14, the nodes

delimited by an ellipse with dashed line indicate the

actions that are enabled for execution in the current

instance state represented by the tree. The labeled ar-

rows signalize the start or the end of the execution of

an action

. So, S(a) signalizes the start of the action

a, while F(a) signalizes the end of the same action.

The start or ﬁnish of the execution of an action in

an instance modiﬁes the status of a leaf node in its

navigation tree. Each modiﬁcation in the status of a

leaf node in a navigation tree requires the update of

status of its predecessor nodes. To enable this opera-

tion, each node keeps a pointer to its parent node, be-

sides the pointers to the left child and the right child

nodes. The status node conﬁguration in a navigation

tree determines the current state of the instance; thus,

a change in the instance state generates a new set of

actions currently enabled for execution. The status of

a node that represents an alternative composition op-

erator is speciﬁed by the status of its child nodes in

the following way:

• Started : if the left or the right child has status

started ;

• Finished : if the left or the right child has status

ﬁnished ;

• Canceled : if the left and the right child has sta-

tus canceled.

Figure 5: State transitions for a branch rooted at an operator

of sequential composition.

In Figure 3(2), the rules state that the process rep-

In NPTool, the actions of a process may not have an

instantaneous execution, i.e., the execution can be distin-

guished by a start event and by an ending event.

resented by x.y executes ﬁrst x and, after x have been

ﬁnished successfully, it starts the execution of y. Fig-

ure 5 shows the possible state changes in a branch

rooted at a sequential composition (“.”) operator.

The status of a node with a sequential composition

operator is speciﬁed by the status of its child nodes in

the following way:

• Started : if the left child has status started or if

the left child has the status ﬁnished and the right child

has status started. The right child will never have sta-

tus started while the left child does not have status

ﬁnished ;

• Finished : if the left and the right child has sta-

tus ﬁnished ;

• Canceled : if the left and/or the right child has

status canceled.

The process term xky indicates that the terms x and

y will be executed parallelly, i.e., it is possible to ex-

ecute an initial transition of x (x

−→

√

or x

−→ x

)

or a initial transition of y. This behavior is formally

speciﬁed by the rules in Figure 3(3). The set of all

the possible states originated by an expression involv-

ing the parallel composition (“k”) operator is large, as

Figure 6 shows. The status of a node that represents

the parallel composition operator is speciﬁed by the

status of its child nodes in the following way:

• Started : if the left or the right child has status

started ;

• Finished : if the left and the right child has sta-

tus ﬁnished ;

• Canceled : if the left and/or the right child has

status canceled.

The conditional execution, negative conditional

execution, unlimited repetition, number limited rep-

etition and function limited repetition operators are

not treated as nodes in the navigation tree. They are

treated as attributes of nodes, since they inﬂuence the

execution of the complete branch rooted at the node

with which they are associated. If a node have a rule

or a function associated with it, then it is necessary

to execute this rule or function before “visiting” the

node in the navigation algorithm. The execution of

the rule or function, like in the case of atomic ac-

tions, is a responsibility of the applications that use

the NPTool. When an action or a process term is

delimited by some of the two conditional execution

operators, the rule that conditionates the execution is

attributed to the node that represents the delimited ac-

tion or to the root node of the delimited process term.

In the example of Figure 7(a), the execution of ac-

tion a is conditioned by the return value true of rule

, while the execution of b is conditioned by the re-

turn value false. In this example, the return value of r

was true; so, after ﬁnishing the execution of r

, only

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL

327

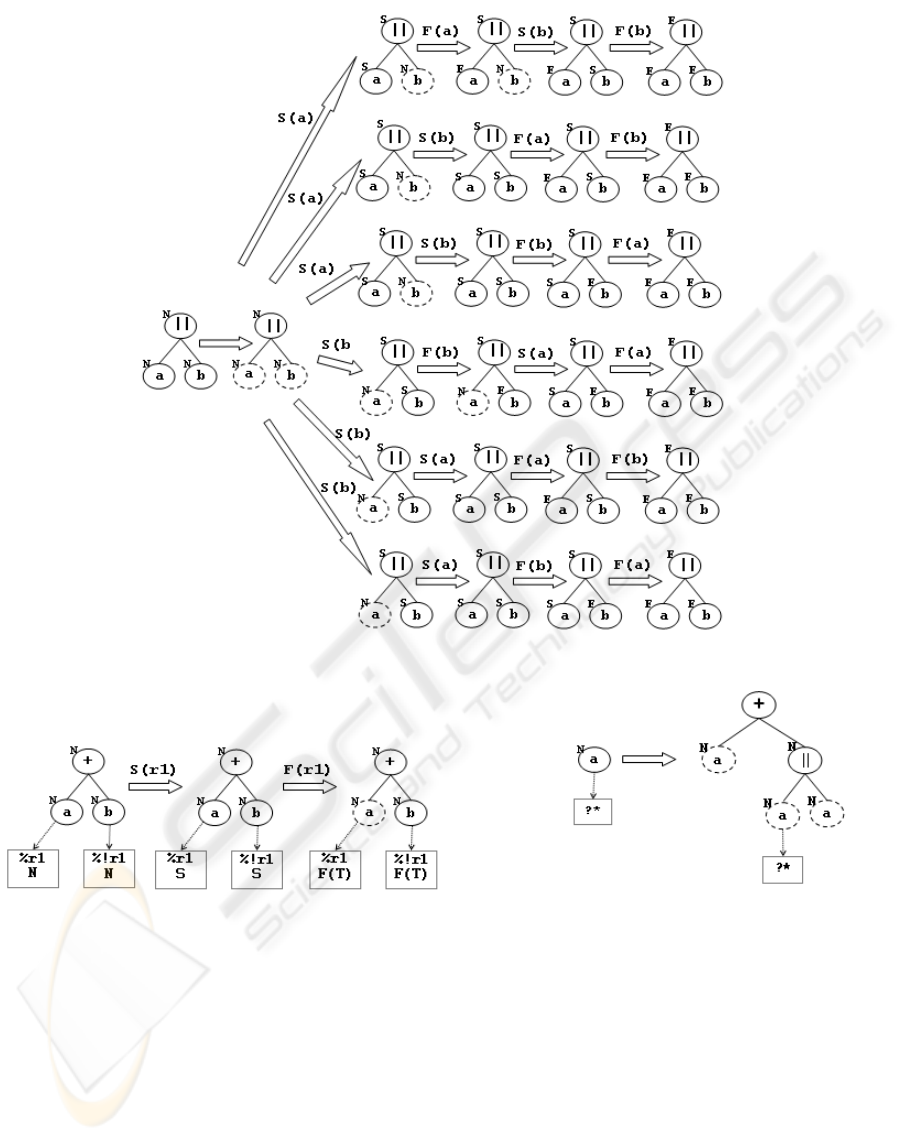
Figure 6: State transitions for a branch rooted at an operator of parallel composition.

(a) (b)

Figure 7: Treatment of (a) node associated with rules or functions and (b) nodes with unlimited repetition.

the action a was enabled to be executed.

In the case of repetitive actions or process terms,

the node that represents the action or term is labeled as

repetitive, and if this repetition is limited by a number

or a function, this number or function will be associ-

ated with the node. Figure 7(b) shows how a repeti-

tive node is treated by “expanding” it in an equivalent

branch.

The inspection of a navigation tree in order to get

enabled steps to execution in an instance is also con-

trolled by the transition rules expressed in Figure 3;

the rules are used to determine how the nodes of the

tree should be visited. The execution monitor starts

to visit the navigation tree from its root node. Ac-

cordingly the current status of the tree nodes, the nav-

igation returns a set of steps currently enabled to be

executed in the instance.

Only the basic operators of NPDL are kept in the

navigation tree. The other operators are treated by

a mapping algorithm that removes them of the nav-

igation tree, replacing them by an equivalent branch

containing only basic operators. Figures 8 and 9 show

how nodes rooted at non-basic NPDL operators in the

navigation tree can be replaced by other equivalent

ICE-B 2008 - International Conference on e-Business

328

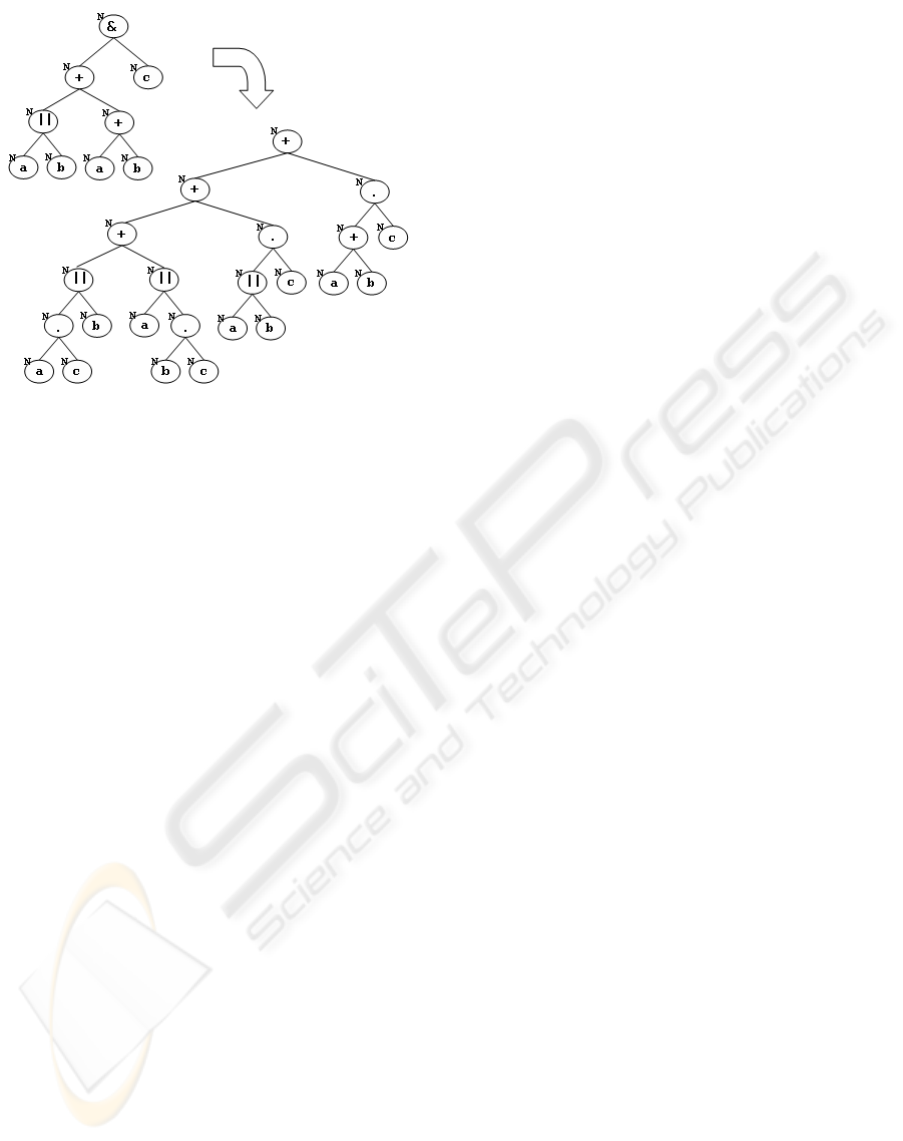
Figure 8: Treatment of a branch rooted at a multi merge

composition operator.

branches.

Processes that involve in their deﬁnition a refer-

ence to other processes are treated by a simple substi-

tution. The navigation tree for the referred process is

created and “connected” to the navigation tree of the

instance, replacing the node that represents the pro-

cess. After the substitution of the process node by the

tree that represents it, the algorithm for obtaining en-

abled steps is applied on the root node of the referred

process.

The execution of an instance is considered suc-

cessfully complete when the status of the root node of

its navigation tree is set to ﬁnished.

4 EXAMPLE OF EXECUTION

CONTROL

This section illustrates a simulated execution of a pro-

cess instance. It shows how works the navigation that

gets the enabled steps and updates the state of the nav-

igation tree. The process used as example is a simpli-

ﬁed version of a system developed for controlling the

acquisition of items to a library collection.

Consider the set of rules and the set of actions

belonging to the acquisition system that are deﬁned,

respectively, as R = {r

} and A = {a

, a

such that:

• r

checks the completeness of data from acqui-

sition order and the availability of the budget for pur-

chasing;

• a

sorts the order items according to some prior-

ity;

• a

gathers the prices of the order items;

• a

liberates the order for purchasing;

• a

registers the purchase receiving;

• a

registers a problem with the purchase.

The acquisition system can be speciﬁed by the

process P deﬁned in NPDL by the commands:

SET P1 = a1 |* a2 + (a1 |* a2).P1;

SET P = %r1 P1 . a3 . (a4 + a5?* . a4);

The check step of order data is treated as a rule (in

the case, r

). Thus, the execution of the activities in-

volved in the acquisition system will only be enabled

if the order data is valid and there is available bud-

get for the purchase. The subprocess P

encapsulates

the actions of sorting items (a

) and gathering items

price (a

) . The actions are composed by the operator

“|∗”, that indicates that they can be executed in any

order, but not in parallel. Moreover, P

was deﬁned

in a recursive way. This indicates that these actions

can be repeated an unrestricted number of times be-

fore the liberation of the order for purchasing. After

the liberation of the order (action a

), it is possible

that problems occur in the purchase. These problems

are registered in the acquisition process by the action

. The repetition operator “?∗” was used associated

with a

, to represent the possibility of occurring more

than one problem during the purchase.

The initial navigation tree of an instance of acqui-

sition process is represented in Figure 10(a). Each

node has, at the upper left side, a character that indi-

cates one of the following states: “N” (not started),

“S” (started) and “F” (ﬁnished). It is important to no-

tice that, associated with the node that represents the

process P

in the tree, exists the rule r

. Such as the

tree nodes, a rule has a status too. Associated with the

node representing action a

, exists the operator “?∗”,

that indicates that the action can have its execution

repeated.

In the beginning of the execution, the tree is vis-

ited starting on its root node (distinguished by a

dashed line in Figure 10(a)). While the navigation

algorithm is visiting the tree nodes, it comes across

the rule r

and it adds the rule in the set of currently

enabled steps to execution. Since the execution of the

other steps depends on the execution of step condi-

tioned by r

, no other step can be executed at ﬁrst.

Considering now that r

have been executed and

its return value was true, the algorithm for getting the

currently enabled steps is applied on the node associ-

ated with r

in the tree and ﬁnds the node x in Fig-

ure 10(b). The node x represents the process P

and,

as explained previously, it needs to be expanded by

replacing the node by its navigation tree. Figure 11(a)

shows the tree after the substitution.

Continuing the visitation to the tree nodes, the al-

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL

329

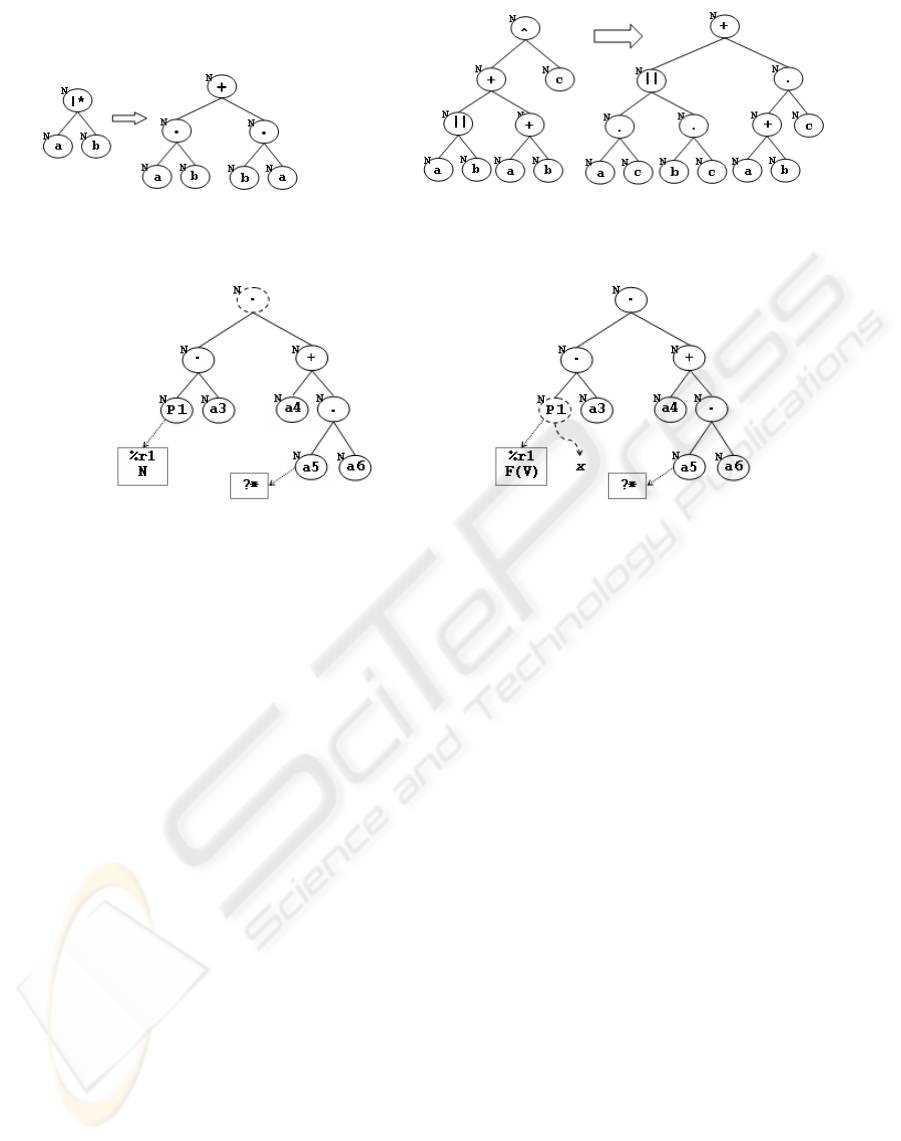
(a) (b)

Figure 9: Treatment of a branch rooted at the operators (a) interleaved parallel and (b) discriminator composition.

(a) (b)

Figure 10: (a) Initial state of the tree for an instance of acquisition process. (b) Tree after the execution of the rule r

gorithm detects the existence of the operator “|∗” in

two different places in the tree (nodes x and y in Fig-

ure 11(a)). Since the operator “|∗” is not a NPDL

basic operator, it requires a special treatment.

In NPDL, a process term like a|∗b is equivalent

to a.b + b.a. Figure 11(b) shows the navigation tree

after mapping the operators “|∗”. After the map-

ping, the visitation algorithm is able to identify the

currently enabled steps to execution. As the distin-

guished nodes in Figure 11(b) shows, there are two

enabled steps to execution in the navigation tree: ac-

tions a

and a

Consider that, after the execution of r

, the action

have been executed, and the algorithm for propa-

gating the status update through the tree nodes is ap-

plied on the nodes x and z of Figure 11(b). In the

resulted tree, only the action a

is enabled to execu-

tion; Figure 12(a) shows the tree after the execution

of a

In a navigation tree, branches rooted at a node

whose status have already been deﬁned as ﬁnished

and which do not have enabled steps to execution can

be removed from the tree. The goal of this removal is

the optimization of the main memory occupied by the

storage of the trees. Figure 12(b) illustrates the tree

resulted by the removal of the inaccessible branches

of the tree in Figure 12(a); the nodes distinguished by

the background color gray are the nodes that had their

children removed.

The navigation for getting the currently enabled

steps to execution detects the node y in Figure 12(b),

which once more represents the process P

. The node

is replaced by the navigation tree of process P

, result-

ing the tree in Figure 13(a). In the tree in Figure 13(a),

the nodes x and y represents the operators “|∗”, which

must be mapped to basic operators, resulting the tree

in Figure 13(b). In the tree in Figure 13(b), the en-

abled steps are the actions a

(nodes w and y), a

(nodes x and z) and a

(node v). If the chosen step

for execution is the action a

, the application of the

algorithm for propagating the status update through

the tree nodes over the node v in Figure 13(b) results

in the tree in Figure 14(a).

When the algorithm of navigation ﬁnds the node

y in the tree in Figure 14(a), it will apply the map-

ping of the operator “?∗” associated with the action

, resulting the tree in Figure 14(b). In this tree, the

currently enabled steps to execution are the actions a

and a

. The tree in Figure 14(c) is obtained by execut-

ing the action a

and applying algorithm for propagat-

ing the status update over the node w in Figure 14(b).

The root node of the tree in Figure 14(c) has the sta-

tus ﬁnished, which indicates that the execution of the

process instance was terminated successfully.

ICE-B 2008 - International Conference on e-Business

330

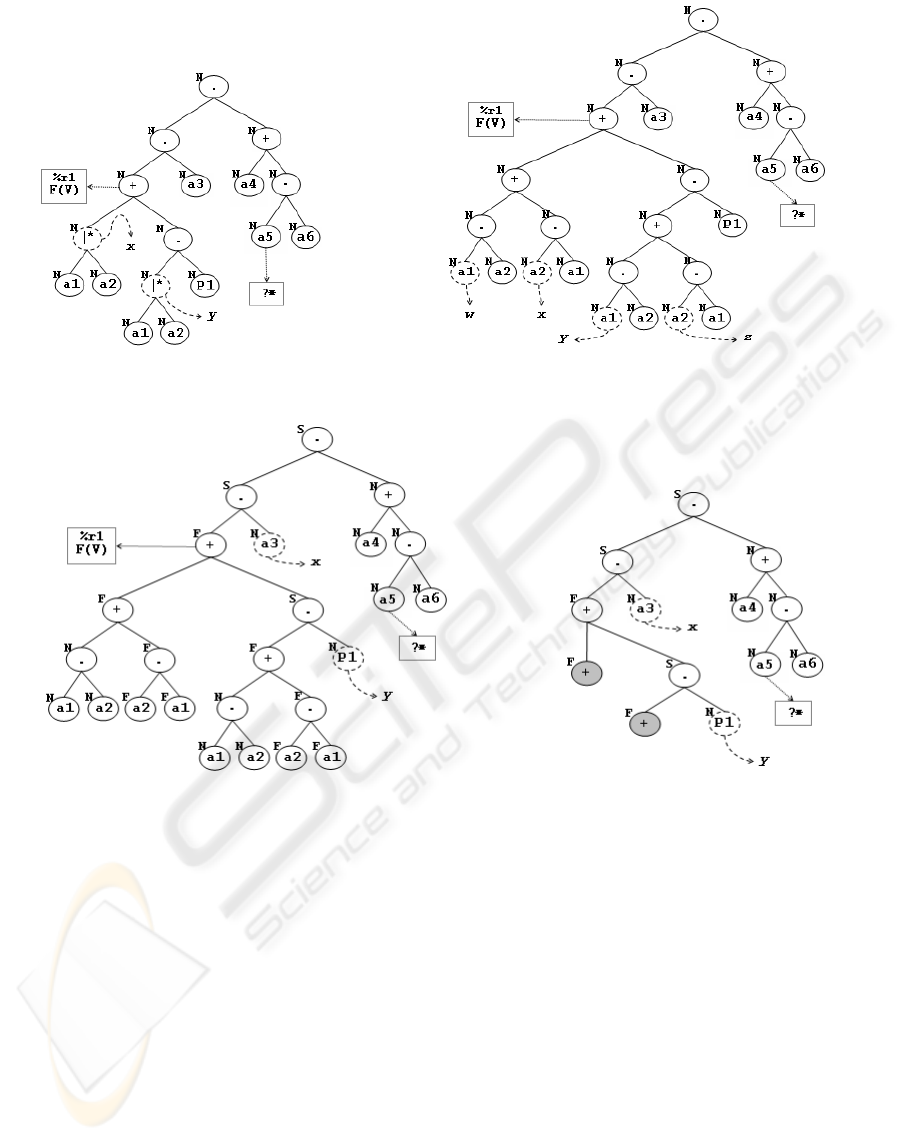
(a) (b)

Figure 11: (a) Navigation tree after the substitution of P

and, next, (b) after the substitution of operators “|∗”.

(a) (b)

Figure 12: Navigation tree (a) after the execution of actions a

and a

, and (b) after the removal of inaccessible branches.

5 CONCLUSIONS

NavigationPlanTool is a framework that uses NPDL

and a relational database model to specify business

processes and control their instantiations and execu-

tions. The NPDL language is based on the concept of

navigation plan of the RiverFish architecture as well

as in the operators of processes algebra.

The simplicity of the relational database model

(used by NPTool for the storage of processes, in-

stances and its executions) is consequence of the

adoption of processes algebra as formal basis, due

to its algebraic and textual form. Albeit simple, this

model has proved to be quite ﬂexible, since it allows

the enrichment of the expressiveness of NPDL (by in-

cluding new operators in the language) without caus-

ing impact to the data structure. This model also

allows us to make reuse of the processes deﬁnition

between different applications that use the NPTool,

as it can be viewed as a common repository of pro-

cesses. Moreover, the compositional characteristic of

processes algebra makes the composition of great pro-

cesses from smaller ones possible. This constitutes an

important aspect for business processes, in which the

reuse of deﬁnitions is a common occurrence.

The implementation of NPDL as an extension of

the SQL language provided by NavigationPlanTool

allows its easy integration to traditional information

systems, which already have mechanisms that facili-

tate the access to RDBMSs. In addition to that, the

storage of the processes deﬁnition data, instances and

its executions in a relational database makes the Nav-

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL

331

(a) (b)

Figure 13: Navigation tree (a) after substituting P

and, next, (b) after the substitution of the operators “|∗”.

(a) (b) (c)

Figure 14: Navigation tree (a) after executing action a

, (b) after the removal of inaccessible branches and mapping operator

“?∗”; next, (c) after executing action a

igationPlanTool a tool that can be used by informa-

tion systems that require scalable and reliable control

to execute business processes. These reliability and

scalability are assured by the use of a RDBMS.

Currently NPTool has been used in three im-

portant applications: controlling the acquisition and

lending of library items at University of S

ao Paulo

(USP); managing of clinical exams in the Human

Genoma Institute at USP, and the identiﬁcation of

HIV drug resistance. Details about the latter can

be seen in (Ara

ujo et al., 2008); the referred paper

presents an alternative for mapping of genotypic drug

resistance algorithms rules using NPDL expressions.

Our ongoing research topics include the identiﬁ-

ICE-B 2008 - International Conference on e-Business

332

cation and reuse of control-ﬂow patterns in business

processes, data ﬂow management for business pro-

cesses and automated generation of NPDL expres-

sions from graphical representations.

REFERENCES

Aalst, W. (1998). The application of petri nets to workﬂow

management. The Journal of Circuits, Systems and

Computers, 8(1):21–66.

Aalst, W. and Hofstede, A. (2005). YAWL: Yet another

workﬂow language. Information Systems, 30(4):245–

275.

Aalst, W., Hofstede, A., Kiepuszewski, B., and Barros, A. P.

(2003). Workﬂow Patterns. Distributed and Parallel

Databases, 14(1):5–51.

Ara

ujo, L. V., Sabino, E. C., and Ferreira, J. E. (2008). HIV

drug resistance analysis tool based on process alge-

bra. In Proceedings of the 2008 ACM Symposium on

Applied Computing, Fortaleza, Brazil, March 16-20,

2007, pages 1358–1364. ACM.

Beaudouin-lafon, M., Mackay, W. E., Andersen, P.,

Janecek, P., Jensen, M., Lassen, M., Lund, K.,

Mortensen, K., Munck, S., Ratzer, A., Ravn, K.,

Christensen, S., and Jensen, K. (2000). CPN/Tools:

A post-WIMP interface for editing and simulating

coloured petri nets.

Braghetto, K. R., Ferreira, J. E., and Pu, C. (2007). Us-

ing control-ﬂow patterns for specifying business pro-

cesses in cooperative environments. In Proceedings

of the 2007 ACM Symposium on Applied Computing,

Seoul, Korea, March 11-15, 2007, pages 1234–1241.

ACM.

Ferreira, J. E., Takai, O. K., Braghetto, K. R., and Pu, C.

(2006). Large scale order processing through navi-

gation plan concept. In Proceedings of the IEEE In-

ternational Conference on Services Computing, pages

297–300. IEEE Computer Society.

Ferreira, J. E., Takai, O. K., and Pu, C. (2005). Integration

of collaborative information system in internet appli-

cations using riverﬁsh architecture. In Collaborate-

Com. IEEE.

Fokkink, W. (2000). Introduction to Process Algebra.

Springer.

Leymann, F., Roller, D., and Schmidt, M.-T. (2002). Web

services and business process management. IBM Sys-

tems Journal, 41(2):198–211.

Puhlmann, F. and Weske, M. (2005). Using the pi-calculus

for formalizing workﬂow patterns. In Springer, editor,

Third International Conference on Business Process

Management (BPM 2005), pages 153–168.

BUSINESS PROCESSES MANAGEMENT USING PROCESS ALGEBRA AND RELATIONAL DATABASE MODEL

333