AN EFFICIENT METHODOLOGY TO LIMIT PATH LENGTH

GUARANTEEING ANONYMITY IN OVERLAY NETWORKS

Juan Pedro Mu˜noz-Gea, Josemaria Malgosa-Sanahuja, Pilar Manzanares-Lopez

Juan Carlos Sanchez-Aarnoutse and Joan Garcia-Haro

Department of Information Technologies and Communications, Polytechnic University of Cartagena

Campus Muralla del Mar, 30202, Cartagena, Spain

Keywords:

Anonymity, multi-hop paths, overlay networks.

Abstract:

An alternative to guarantee anonymity in overlay networks may be achieved by building a multi-hop path

between the origin and the destination. However, one hop in the overlay network can consist of multiple

Internet Protocol (IP) hops. Therefore, the length of the overlay multi-hop path must be reduced in order to

maintain a good balance between the cost and the beneﬁt provided by the anonymity facility. Unfortunately,

the simple Time-To-Live (TTL) algorithm cannot be directly applied here since its use could reveal valuable

information to break anonymity. In this paper, a new mechanism which reduces the length of the overlay

multi-hop paths is presented. The anonymity level is evaluated by means of simulation and good results are

reported.

1 INTRODUCTION

Over the last years, we have witnessed the emergence

of different types of overlay networks in the Internet

(Tsang et al., 2007). In these new scenarios, con-

cerns about anonymity signiﬁcantly arise among the

user community. Anonymity refers to the ability to

do something without revealing one’s identity (in this

case, the user’s) (Pﬁtzmann and Hansen, 2007). The

simplest solution to provide anonymity in overlaynet-

works is to select several relay nodes in the route from

the sender to the receiver. In this way, even if a local

eavesdropper observes a message being sent by a par-

ticular user, it can never be sure whether the user is

the current sender, or if the message is forwarded by

a relay node.

Similar techniques have been widely studied in the

past to provide anonymity in IP networks. One of

them is Crowds (Reiter and Rubin, 1998), in which

each node decides to deliver the message to an inter-

mediate or destination node by ﬂipping a biased coin

(with probabilities p

and 1− p

respectively). Nev-

ertheless, the use of this mechanism in overlay net-

works is not appropriate, because the forwarding pro-

cedure is not limited in any way, and as it known, in

overlay networks neighbour nodes are connected by

means of logical links, each one comprised of an ar-

bitrary number of physical links. Therefore, a serious

increase in the length of the overlay path among the

origin and the destination nodes could imply an expo-

nential cost, in terms of bandwidht consumption and

nodes overload.

A straightforwardimplementation to limit the path

length makes use of the Time-To-Live(TTL) ﬁeld, but

there are multiple situations in which this implemen-

tation will immediately reveal to an ”attacker” who

the initiator node is. This paper proposes a mecha-

nism that limits the length of overlay multi-hop paths

without using a TTL (Time-To-Live) scheme. Fur-

thermore, simulation results show that this mecha-

nism presents a degree of anonymity equivalent to

Crowds.

The remainder of the paper is organized as fol-

lows. Section 2 overviews some relevant works about

anonymous systems. Section 3 presents the different

requirements that must be satisﬁed in order to limit

the path length. Section 4 introduces our proposal,

called the Always Down-or-Up (ADU) mechanism.

In section 5 our algorithm is evaluated by means of

simulation. In section 6 the anonymity level achieved

by the proposed mechanism is evaluated by means of

simulation. Finally, section 7 concludes the paper.

205

Pedro Muñoz-Gea J., Malgosa-Sanahuja J., Manzanares-Lopez P., Carlos Sanchez-Aarnoutse J. and Garcia-Haro J. (2008).

AN EFFICIENT METHODOLOGY TO LIMIT PATH LENGTH GUARANTEEING ANONYMITY IN OVERLAY NETWORKS.

In Proceedings of the International Conference on Security and Cryptography, pages 205-208

DOI: 10.5220/0001916202050208

 SciTePress

2 RELATED WORK

The seminal paper on anonymous sytems was written

by David Chaum (Chaum, 1981). He proposed a sys-

tem for anonymous email based on the so called mix

networks. A mix node shufﬂes a batch of messages

and delivers them in random order. This design has

been followed by many anonymous systems. The ﬁrst

widely used implementation of mix networks was the

Type I cypherpunk anonymous remailers (Goldberg

et al., 1997), using PGP (Zimmermann, 1995) encryp-

tion to wrap email messages and deliver them anony-

mously. They were followed by MixMaster (M¨oller

et al., 2003), and then MixMinion (Danezis et al.,

2003).

Although the mix design has been quite inﬂuen-

tial, there are a number of notable alternatives. A net-

work that uses a different approach is Crowds (Re-

iter and Rubin, 1998), designed for anonymous web

browsing. Brieﬂy, Crowds nodes forward web request

to each other at random, executing a form of a random

walk.

3 BACKGROUND

In Crowds, the initiator node creates a packet con-

taining a random path identiﬁer, the IP address of the

responder and the data. Then, it ﬂips a biased coin.

With probability 1 − p

is the probability of for-

warding and it is a parameter of the system) it delivers

the message directly to the responder or destination

node, and with probability p

it chooses randomly

the next relay node. Each node decides- based on p

whether to forward it to the responder or to another

(randomly chosen) relay node. With this original al-

gorithm the forwarding procedure is not limited and,

as we previously pointed out, it could be a tragedy re-

garding communication costs in an overlay scenario.

A possible solution is to restrict the maximum

length of the paths. The system operates as the tradi-

tional scheme but, when the number of hops reaches

a certain limit (called S), the path will be directed

towards the destination node. A straightforward im-

plementation consists of using a time-to-live (TTL)

ﬁeld, initially set to S, and processing it like in IPv4

networks (Postel, 1981). However, there are multiple

situations in which this implementation will immedi-

ately reveal to a ”corrupt” node whether the prede-

cessor node is the initiator or not. Therefore, we can

conclude that the TTL methodology is not appropriate

to limit the length of multi-hop paths.

4 PROPOSED MECHANISM

The algorithm proposed in this work, as in Crowds,

is based on the random-walk procedure. However,

the variance associated to the length of the multi-hop

paths is smaller than that in Crowds. Therefore, it

can be viewed as a quasi-deterministic mechanism of

a statistical TTL implementation.

Our ﬁrst attempt is the always-down (AD) algo-

rithm: The path originator chooses a uniform random

number (called u) between 1 and a predeﬁned param-

eter M. If the value of u is equal to 1, the originator

sends the request directly to the destination. Other-

wise, the node forwards the request to a random node

together with the random number u. The next node

performs the same operation but replacing the upper

bound M with the value of u. The mechanism contin-

ues in a recursiveway, decreasing the size of the inter-

val [1, u) in each step. However, with this algorithm

there is still correlation between the random number

u and the hop length: although little values do not

reveal anything about the path length, great ones do,

since they can only appear at the ﬁrst steps of the al-

gorithm.

The opposite algorithm, called always-up (AU)

has the same beneﬁts and drawbacks. Now, at each

step the node chooses a uniform random number be-

tween (u, M]. When a node selects M, the random

walk procedure ends and the request is directly sent

to the responder. In this case, great values of u do not

reveal anything about the path length, but small ones

do, since they can only appear at the ﬁrst steps of the

algorithm.

In order to avoid this critical issue, we propose to

mix both mechanism as follows: The path originator

chooses a random number (called u) between 1 and

M. When this number is equal to 1 or equal to M,

the originator node sends the request to the responder.

If u is lower than a parameter LOW

BORDER, the

algorithm works like AD. However, if u is greater than

a paramater TOP

BORDER, the algorithm operates

like AU. Finally, if u drops between LOW

BORDER

and TOP BORDER, the operation mode (AD or AU)

is chosen randomly.

This new algorithm is called always down-or-up

(ADU) and it is able to statistically limit the length

of the path in an anonymous environment. In order

to speed up the algorithm, we introduce an additional

parameter called e: If the new chosen random num-

ber is smaller than or equal to e (or it is greater than

M − e) the originator node delivers the request to the

responder. Figure 1 represents the full set of parame-

ters used by our algorithm in a numerical straight line.

SECRYPT 2008 - International Conference on Security and Cryptography

206

e LOW

BORDER BORDER

TOP

random

M−e M

updown

Figure 1: Parameters of the algorithm.

Table 1: Values of parameters for speciﬁc

ADU Crowds

l M e p

2 100 21 0.5

3 100 8 0.6667

4 100 3 0.75

5 150 2 0.80

6 350 2 0.8333

Table 2: Variance of the length of the paths.

l ADU Crowds

2 1.3337 2

3 2.3559 6

4 3.4135 12

5 4.5062 20

6 5.5821 30

5 EVALUATION

The random variable l that represents the length of

the path has been evaluated by means of simulation.

Table 1 presents the appropriate values for the param-

eters M and e in order to achieve representativevalues

for l. This table also represents the appropriate values

of p

to achieve the same values of

l in Crowds. It

is known that the mean length of the multi-hop paths

created using the Crowds mechanism follows the ge-

ometrical expression:

l =

1−p

Table 2 presents the variance of the length of the

paths for ADU and Crowds. The variance of the ADU

paths is calculated using:

V(l) = E(l

) − E(l)

(1)

on the other hand, for Crowds it is known that

V(l) =

(1− p

)

(2)

It is observed that the variance in ADU is always

signiﬁcantly smaller than in Crowds. This behaviour

enables to interpret the ADU algorithm like a quasi-

deterministic TTL implementation. Therefore, the

mechanism achieves the target goal.

6 ANALYSIS OF ANONYMITY

The anonymity level achieved by the proposed mech-

anism is evaluated by means of simulation following

the methodology exposed in (Borissov, 2005). This

methodology is based on the use of the entropy as a

measure of the anonymity level. This concept was

presented in (D´ıaz et al., 2002), and it can be sum-

marized as follows: It is assumed that there is a total

number of N nodes,C of them are corrupt and the rest

honest. Corrupt nodes collaborate among them trying

to ﬁnd out who is the origin of the messages. Based

on the information retrieved from corrupt nodes, the

attacker assigns a probability (p

) of being the origin

of a particular message for each node. The degree of

anonymity (d) of the system can be expressed by:

d = −

∑

i=1

log

) (3)

where H

is the maximum entropy of the system,

which is satisﬁed when all honest nodes have the same

probability of being the origin of the message.

If a message goes only through honest nodes the

degree of anonymity will be d|

honest nodes

= d

= 1. If

we assume that the message goes through at least one

corrupt node with probability p

and it crosses only

through honest nodes with probability p

= 1 − p

the mean degree of anonymity of the system is:

d = p

· d|

corrupt nodes

+ p

· d

= p

· d

+ p

(4)

The methodology proposed in (Borissov, 2005)

has been implemented in a simulator written in C lan-

guage. First, in order to obtain an appropriate value

for the number of iterations we simulate an scenario

with

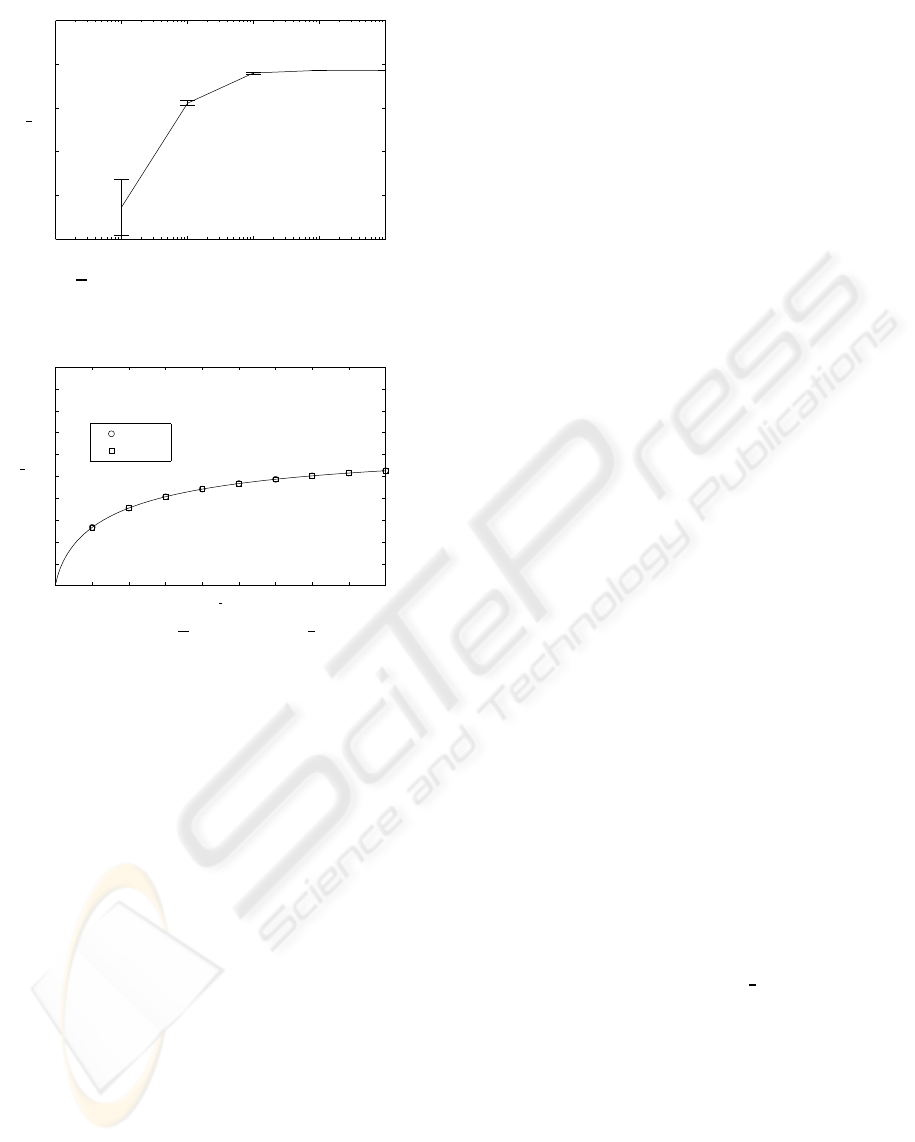
l = 4 for different number of iterations. Figure

2 presents the results with the 95 % conﬁdence in-

tervals. We can see that from 10,000 iterations, the

accuracy of the simulation results is within the 0.1 %

with respect to the stable value. Therefore, in our sim-

ulations the number of iterations is set to 10,000.

Figure 3 compares d for Crowds and ADU when

N=100 and C=10. It represents the anonymity level

according to the mean length of the paths, from 1 to

10. These small values have been selected because,

as it was previously mentioned, our objective is to

achieve shor multi-hop paths. It can be observed that

the degree of anonymity achieved by the ADU al-

gorithm perfectly matches the degree of anonymity

achieved by Crowds.

AN EFFICIENT METHODOLOGY TO LIMIT PATH LENGTH GUARANTEEING ANONYMITY IN OVERLAY

NETWORKS

207

0 10 100 1000 10000 100000

0.75

0.8

0.85

0.9

0.95

Number of Samples

Figure 2: d with conﬁdence intervals as a function of the

number of iterations.

1 2 3 4 5 6 7 8 9 10

0.9

0.91

0.92

0.93

0.94

0.95

0.96

0.97

0.98

0.99

Crowds

ADU

Figure 3: d as a function of l.

7 CONCLUSIONS

In traditional (like Crowds) anonymous networks, the

anonymity is achieved by building a multiple-hop

path between the origin and the destination nodes.

However, the cost associated with the communica-

tion increases dramatically as the number of hops also

increases. Therefore, in these scenarios limiting the

length of the paths is a key aspect of the protocols de-

sign. Unfortunately, the common TTL methodology

cannot be used to this purpose since corrupt nodes can

employ this ﬁeld to extract some information about

the sender identity.

In this work an effetive mechanism to reduce the

variance associated with the length of the random

walks in anonymous overlay scenarios is proposed.

Our study reveals that the variance in ADU is always

smaller than in Crowds. In addition, the degree of

anonymity achieved by ADU is equivalent to Crowds.

Thus, this mechanism is a recommended methodol-

ogy to achieve a good trade-off between cost/beneﬁt

associated with the anonymity in overlay networks.

ACKNOWLEDGEMENTS

This research has been supported by project grant

TEC2007-67966-C03-01/TCM(CON-PARTE-1) and

it is also developed in the framework of ”Programa

de Ayudas a Grupos de Excelencia de la Regi´on de

Murcia, de la Fundaci´on S´eneca, Agencia de Ciencia

y Tecnolog´ıa de la RM (Plan Regional de Ciencia y

Tecnolog´ıa 2007/2010)”. Juan Pedro Mu˜noz-Geaalso

thanks the Spanish MEC for a FPU (AP2006-01567)

pre-doctoral fellowship.

REFERENCES

Borissov, N. (2005). Anonymous routing in structured peer-

to-peer overlays. PhD thesis, University of Califor-

nia at Berkeley, Berkeley, CA, USA. Chair-Eric A.

Brewer.

Chaum, D. L. (1981). Untraceable electronic mail, return

addresses, and digital pseudonyms. Commun. ACM,

24(2):84–90.

Danezis, G., Dingledine, R., and Mathewson, N. (2003).

Mixminion: Design of a type iii anonymous remailer

protocol. In SP ’03: Proceedings of the 2003 IEEE

Symposium on Security and Privacy, page 2, Wash-

ington, DC, USA. IEEE Computer Society.

D´ıaz, C., Seys, S., Claessens, J., and Preneel, B. (2002).

Towards measuring anonymity. In Dingledine, R. and

Syverson, P., editors, Proceedings of Privacy Enhanc-

ing Technologies Workshop (PET 2002). Springer-

Verlag, LNCS 2482.

Goldberg, I., Wagner, D., and Brewer, E. (1997). Privacy-

enhancing technologies for the internet. In COMP-

CON ’97: Proceedings of the 42nd IEEE Interna-

tional Computer Conference, page 103, Washington,

DC, USA. IEEE Computer Society.

M¨oller, U., Cottrell, L., Palfrader, P., and Sassaman, L.

(2003). Mixmaster protocol — version 2. draft, july

2003. http://www.abditum.com/mixmaster-spec.txt.

Pﬁtzmann, A. and Hansen, M. (2007). Anonymity, unlinka-

bility, undetectability, unobservability, pseudonymity,

and identity management - a consolidated proposal

for terminology (version v0.30 nov. 26, 2007).

http://dud.inf.tu-dresden.de/Anon

Terminology.shtml.

Postel, J. (1981). RFC 791: Internet Protocol.

Reiter, M. K. and Rubin, A. D. (1998). Crowds: anonymity

for web transactions. ACM Trans. Inf. Syst. Secur.,

1(1):66–92.

Tsang, D. H. K., Ross, K. W., Rodriguez, P., Li, J., and

Karlsson, G. (2007). Advances in peer-to-peer stream-

ing systems [guest editorial]. IEEE Journal on Se-

lected Areas in Communications, 25(9):1609–1611.

Zimmermann, P. R. (1995). The ofﬁcial PGP user’s guide.

MIT Press, Cambridge, MA, USA.

SECRYPT 2008 - International Conference on Security and Cryptography

208