A MULTIPLE BIRTHDAY ATTACK ON NTRU
Raphael Overbeck
∗
EPFL, LASEC, Building INF - Station 14, 1015 Lausanne, Switzerland
Keywords:
NTRU, Public key cryptography, birthday paradox.
Abstract:
In this paper we view the possibilities to lance a multiple (iterative) birthday attack on NTRU. Recently Wag-
ner’s algorithm for the generalized birthday problem (Wagner, 2002) allowed to speed-up several combinato-
rial attacks. However, in the case of NTRU we can not hope to to apply Wagner’s algorithm directly, as the
search space does not behave nicely. In this paper we show that we can nevertheless draw profit from a mul-
tiple birthday approach. Our approach allows us to attack
ees251ep6 parameter set on a computer with only
2
52
Bits of memory and about 2
9
times faster as with Odlyzko’s combinatorial attack – this is an improvement
factor about 2
43
in space complexity. We thus contradict the common believe, that in comparison to com-
putational requirements, the “storage requirement is by far the larger obstacle” (Howgrave-Graham, 2007) to
attack NTRU by combinatorial attacks. Further, our attack is about 2
7
times faster than the space-reduced
variant from (Howgrave-Graham, 2007) employing the same amount of memory.
1 INTRODUCTION
The asymmetric NTRU encryption system (NTRU)
(Hoffstein et al., 1998) is a well known cryptosys-
tem, which to our knowledge is secure for large pa-
rameter sets, e.g. with N ≈ 500. For small parameter
sets, however, NTRU was subject to several attacks
connected to lattice theory like attacks on alterna-
tive keys (Coppersmith and Shamir, 1997), exploita-
tion of decryption errors (Howgrave-Graham et al.,
2003) and the ones using dimension reduced lattices
or zero-forcing (May and Silverman, 2001; Silver-
man, 1999). These attack exploit the fact, that the pri-
vate NTRU key is presumably the shortest vector in a
lattice which can be deduced from the public NTRU
key. Besides lattice-based attacks, there exists a com-
binatorial attack originally due to Odlyzko, see e.g.
(Howgrave-Graham, 2007). After several iterations
of attacks and countermeasures, NTRU was consid-
ered for standardization (P1363.1/D9, 2003). In that
proposal, parameters of NTRU are chosen such that
the combinatorial attack is (theoretically and practi-
cally) the fastest one. This is the case if the NTRU
parameters have p = 2 with a small d
f
.
∗
This work was funded by DFG grant OV 102/1-1
1.1 Our Contribution
We concentrate on adapting the attacks on NTRU to
machines with limited storage capacity and thus al-
lowing distributed attacks on NTRU. Evaluating the
possible applications of an multiple birthday attack
on NTRU, we reduce the memory requirements of
a combinatorial-only attack. This is an important
issue: N. Howgrave-Graham states in (Howgrave-
Graham, 2007) that the large storage requirements of
Odlyzko’s attack is “by far the larger obstacle” than
the runtime for attacking NTRU with today’s hard-
ware.
A direct application of the standard solution for
generalized birthday paradox to NTRU is not pos-
sible: The probability, that the secret NTRU vector
remains in the search space during the iterations of
Wagner’s algorithm is too small to allow an efficient
attack. We highlight this problem and present a work-
around which keeps track of the success probability
during the attack.
To perform a multiple birthday attack, we split the
secret NTRU vector f into eight parts instead of two
in Odlyzko’s attack. Further, we guess a permutation
of the positions of the secret g, such that the first posi-
tions of g = fH are zero, where H is the public NTRU
key. Since there are many ways to split up the secret
vector f into eight parts, we can search the space of
possible solutions by an iterative birthday approach:
237
Overbeck R. (2008).
A MULTIPLE BIRTHDAY ATTACK ON NTRU.
In Proceedings of the International Conference on Secur ity and Cryptography, pages 237-244
DOI: 10.5220/0001916602370244
Copyright
c
 SciTePress

We search for those splits of f, which lead to a g = fH
with the first positions zero. This can be done by gen-
erating first a list of vectors of weight one fourth of
the weight of f with the first ℓ
[1]
positions zero via
the birthday approach. Then, we can search the sum
of pairs of such vectors, which are zero on the first
ℓ > ℓ
[1]
positions and have the half weight of f. In
the last part of the attack, we can relax the “birthday”
property, searching for those pairs of the latter vec-
tors, which sum to a vector with the first ℓ + µ posi-
tions binary. Balancing ℓ
[1]
,ℓ and µ, we can be sure,
that the correct f is among the generated vectors. This
way we obtain sets of almost the same size at each it-
eration and thus an attack, which requires much less
memory than Odlyzko’s attack. Further, such an at-
tack is competitive with the fastest known NTRU at-
tack (Howgrave-Graham,2007) in terms of product of
time and space and even better than the space reduced
variant presented in the same paper.
1.2 Related Work
At CRYPTO 2007, N. Howgrave-Graham showed
that the security level for the NTRU parameters
proposed in (P1363.1/D9, 2003) is lower than in-
tended (Howgrave-Graham, 2007). For his attack,
Howgrave-Graham used a hybrid lattice-reduction
and combinatorial attack against NTRU. By heuris-
tic arguments he concludes, that he can attack the
ees251ep6 parameter set in 2
76.2
modular additions
on a machine with 2
65.6
bits of memory or in 2
89.2
modular additions on a machine with 2
53.6
bits of
memory. Unfortunately, so far we are not able to com-
bine both approaches since Howgrave-Graham uses
the concept of s-admissible vectors, which prevents
an iterative birthday approach in the search part of his
attack.
1.3 Organization
In the next section we recall NTRU and the basic nota-
tions. Then, we revise the generalized birthday para-
dox and view it’s application to NTRU. To conclude,
we give numbers and a comparison to the other at-
tacks on NTRU.
2 PRELIMINARIES
In this paper we view only integer lattices, i.e. sub-
vector spaces of Z
N
. We will call wt(f) the (Ham-
ming) weight of a vector f ∈ Z
N
, which corresponds
to the number of non-zero entries in f. If J is a sub-
set of the positions of f, we write f
J
= (f
i
)
i∈J
. For an
introduction into lattice theory see (Micciancio and
Goldwasser, 2002).
NTRU according to (P1363.1/D9, 2003) works as
follows: System parameters are three primes N,q and
p = 2. NTRU uses the ring R = Z[X]/(X
N
− 1). The
elements of that ring are identified with their unique
representations in Z[X] of degree less than N. We will
denote as weight wt( f) of a polynomial f ∈ R the
number of non-zero coefficients. The NTRU secret
key are two binary polynomials f, g ∈ R of weight
d
f
,d
g
respectively. There are various variants of
NTRU. In this paper we concentrate on the one, where
the public key is given as h = ( f
−1
g mod q), where
“mod q” means reduction of the coefficients modulo
q. All attacks on one variant of NTRU may usually be
adapted for other variants.
A description how NTRU en- and decryption
work can be found, e.g., in (Hoffstein et al., 1998;
Howgrave-Graham et al., 2003). However, since at-
tacks on NTRU ciphertexts usually can be adapted to
attack the secret keys and vice versa, this paper deals
with attacks on the secret NTRU keys, only. We thus
omit giving details on en- and decryption.
The NTRU lattice is obtained from a matrix rep-
resentation of multiplications in R . We can easily
deduce a (cyclic) matrix H ∈ F
N×N
q
representing the
multiplication of polynomials with h in R . With the
N-dimensional identity matrix Id
N
we obtain:
C
NTRU
:= f

Id
N
H

≡ (f,g) mod q (1)
for the coefficient vectors f, g of f and g. Note
that

Id
N
H

defines a double-cyclic code over
F
q
. To obtain the NTRU lattice out of the matrix

Id
N
H

, vectors allowing the reduction of fH
modulo q are added and in some cases, f is scaled
by an α:
L
NTRU
:=

αId
N
H
0 qId
N

(2)
According to the Gauss-heuristic, (αf,g) can be as-
sumed to be the shortest vector in the NTRU lattice
if α is properly chosen (up to double-cyclic shifts).
Most attacks aim to find this vector either by lattice
reduction or by a combinatorial approach. In the fol-
lowing we will take α = 1, as this is a suitable value.
3 THE GENERALIZED
BIRTHDAY PARADOX
Many combinatorial attacks could be sped-up by
Wagner’s solution for the generalized Birthday para-
SECRYPT 2008 - International Conference on Security and Cryptography
238

dox. Wagner’s main theorem (Wagner, 2002) can be
summarized as follows:
Theorem 3.1 (q-Generalized Birthday Prob-
lem). Let r,a ∈ N with (a + 1)|r and the sets
L
1
,L
2
,··· ,L
2
a
⊆ F
q
r
be of cardinality q
r
a+1
, then, a
solution of the equation
2
a
∑
i=1
x
i
= 0 where x
i
∈ L
i
, (3)
can be found in O (2
a
q
r
a+1
) operations (over F
q
r
).
The algorithm proposed by Wagner is iterative: Fist,
he searches for partial collisions of the sets L
i
and
L
i+2
a−1
, i = 1,··· ,2
a−1
, that is, such pairs (x
i
,x
i+2
a−1
)
that LSB
r
a+1
(x
i
+ x
i+2
a−1
) = 0. This way, one obtains
2
a−1
Lists with approximately 2
r
a+1
pairs where the
last
r
a+1
entries are zero and can be omitted in the
next step. A recursive application of this step leads to
a solution of Equation (3).
Proof. (Theorem 3.1). Let L
1
and L
2
be two lists
of n-vectors with q
ℓ
elements, then L
1
× L
2
contains
about q
2ℓ
elements (x
1
,x
2
) and thus about q
ℓ
elements
with (x
1
+ x
2
)
{1,···,ℓ}
= 0. We can generate the latter
elements as follows: We sort the elements of L
1
and
L
2
in lexicographic order, which takes O (q
ℓ
log(q
ℓ
))
operations.
2
Now, we can for each element x
1
∈ L
1
look up the elements in L
2
with the same value,
which takes O (|L
1
| · log|L
2
|) = O (q
ℓ
log(q
ℓ
)) opera-
tions again. We can apply the argument iteratively,
which concludes the proof.
In general, the q-generalized birthday paradox al-
lows to find one solution among many possible in
quite efficient time: The set of elements is L
1
×
L
2
× · · · × L
2
a
and thus of size q
2
a
r/(a+1)
with about
q
2
a
/(a+1)
solutions of Equation 3. By Wagner’s
algorithm, we can find one of these solutions in
O (2
a
q
r/(a+1)
) operations instead of O (q
r/2
) opera-
tions with the standard birthday attack.
A direct application to NTRU is not possible. Let
us view for example the ees251ep6 parameter set
(N = 251,q = 197,d
f
= 48,d
g
≈ N/2). Here we
could try to set a = 3 and
L
i
=
n
xH | x ∈ { 0,1}
N
,wt(x) = d f/8 = 6
o
.
2
Here and in the following, any criteria for sorting is
valid. One could, e.g., take lexicographic ordering or maybe
the evaluation of a non-cryptographic hash. We will assume
that sorting a list M , e.g. by “Smoothsort”, costs the same
time as computing the sorting criteria for each element.
However, in the worst case, sorting costs O (|M | · log|M |)
operations.
We get that |L
i
| =

N
6

≈ q
5
≈ 2
41
and could thus hope
to generate binary vectors f, such that f · H is zero at
some 20 = 5 · (a + 1) positions by the q-generalized
birthday paradox. In a random lattice, we would ex-
pect, that there are about 2
20
such vectors, so that we
could assume, that we can find the secret NTRU vec-
tor with probability 2
−20
, if the chosen 20 positions of
g are zero. However, this is not true: There are

d f
d f/2

ways to split the secret NTRU vector f into two parts
f = x
1
+ x
2
of weight d f/2. Thus, the probability that
there is a x
1
, such that x
1
· L
NTRU
is zero at the last 10
position is only

d f
d f/2

· q
−10
< 2
−31
. The probability,
that such a x
1
splits nicely again is

d
f
/2
d
f
/4

·q
−5
< 2
−16
,
turning an attack impossible. In the next section we
will explain how to work around this problem.
4 A MULTIPLE BIRTHDAY
ATTACK FOR NTRU
To apply a multiple birthday attack to NTRU, we have
to ensure that at each iteration there is at least one el-
ement in the search space, which leads to the secret
vector g. By multiplying L
NTRU
with a permutation
matrix P we can assume without loss of generality
that the first positions of g are zero. Our goal is to
generate a list L of N-vectors f of weight d
f
with the
first ℓ ∈ N positions of g = fH zero and the next µ ∈ N
positions binary by applying the birthday paradox it-
eratively like in Wagner’s algorithm. However, in the
NTRU case, numbers and probabilities do not behave
nicely, so that we can not apply the generalized birth-
day paradox directly – as explained in the previous
section. Nevertheless, we can apply the principle.
The key issue of our attack is to balance parame-
ters in a way, such that with sufficient probability, the
secret NTRU vector stays in the search space at each
stage of the multiple birthday attack. For the ease of
presentation we will assume that 8|d
f
.
4.1 An Approach with Symmetric Sets
We will denote with x
1
,x
2
a split of f into two vectors
of weight d
f
/2 and x
1
+ x
2
= f, then we will split up
these vectors into smaller parts until we have split f
into 8 parts, see Figure 4.1.
Each part x
[2]
i
is in the set
L
[2]
i
:=
n
x
[2]
∈ {0,1}
N
| wt(x
[2]
) = d
f
/8
o
,
i = 1,··· ,8. As all sets L
[2]
i
look the same, we use the
term “symmetric” sets. The principle how to generate
L out of the L
[2]
i
is given in Figure 4.2.
A MULTIPLE BIRTHDAY ATTACK ON NTRU
239

L
[2]
1
L
[2]
2
)
L
[1]
1
.
.
.
)
L
[1]
2











L
1
)
L
[1]
3
.
.
.
L
[2]
8
)
L
[1]
4











L
2































L =
n
f ∈ {0,1}
N
| wt(f) = d
f
∧ (fH)
{
1,···,ℓ,ℓ+1···ℓ+µ}
∈ {0}
ℓ
× {0,1}
µ
o
Figure 4.2: Scheme of the multiple birthday attack.
f =























































x
1
=























x
[1]
1
=





x
[2]
1
+
x
[2]
2
+
x
[1]
2
=





x
[2]
3
+
.
.
.
+
x
2
=



















.
.
.
+
x
[1]
4
=





.
.
.
+
x
[2]
8
Figure 4.1: Splitting the secret NTRU vector.
We have to assure, that at each step the probabil-
ity that the secret NTRU vector remains in the search
space is not too low. It is obvious, that there are
x
[2]
i
∈ L
[2]
i
, i = 1,··· ,8 such that f =
∑
8
i=1
x
[2]
i
.
In the first iteration we want to generate the sets
L
[1]
i
, i = 1,··· , 4 with |L
[1]
i
| ≈ |L
[2]
i
| such that there
are x
[1]
i
∈ L
[1]
i
of weight d
f
/4 with
∑
4
i=1
x
[1]
i
= f. To
do so, we choose 0 ≤ ℓ
[1]
≤ ℓ and set
L
[1]
i
=
(
x
[1]
∈ {0,1}
N





wt(x
[1]
) = d
f
/4
∧(x
[1]
H)
{
1,···,ℓ
[1]
}
= 0
)
,
i = 1,··· ,4. Note, that x
[1]
1
+x
[1]
2
is a split of x
1
, where
f= x
1
+x
2
is a split of f. There are

d
f
/2
d
f
/4

possible x
[1]
1
.
Thus, the expected number of valid x
[1]
i
contained in
L
[1]
i
is

d
f
/2
d
f
/4

/q
ℓ
[1]
(4)
and should be larger than one. Like in Wagner’s al-
gorithm, L
[1]
i
can be generated from L
[2]
2i
and L
[2]
2i−1
in
time O (|L
[2]
2i
|log
2
|L
[2]
2i
|) by sorting techniques. In the
second stage, we generate the sets
L
i
=

x ∈ {0,1}
N
| wt(x) =
d
f
2
∧ (xH)
{1,···,ℓ}
= 0

,
i = 1,2, which should contain at least one of the vec-
tors which sum up to f. A element (x
1
,x
2
) with
x
1
+x
2
= f will be in L
1
×L
2
with sufficient probabil-
ity if we can expect that there is an element x
1
∈ L
1
,
which matches f in d
f
/2 positions. This is the case if
the expected number

d
f
d
f
/2

/q
ℓ
. (5)
is larger than one. Thus, we have to choose ℓ
[1]
and ℓ
in respective to the Equations (5) and (4) – however,
there is no need to choose 2ℓ
[1]
= ℓ like in Wagner’s
algorithm. To identify f by the last application of the
birthday paradox, we do not longer search for exact
collisions on a subset of the positions of f· H but for a
binary collision in the first ℓ + µ positions, i.e. those
elements (x
1
,x
2
) ∈ L
1
× L
2
, such that (x
1
+ x
2
) · H ∈
L , as defined in Figure 4.2 (otherwise f 6= x
1
+ x
2
).
The cost of the presented multiple birthday attack
is summarized in the theorem below, which we proof
in the appendix. In the theorem, W
1
represents the
costs to sort the sets L
[2]
i
, W
2
the cost, to generate the
L
[1]
i
and W
3
the number of vector operations needed
to generate the sorted sets L
i
. Finally, W
4
gives the
cost to generate L and search it for the secret NTRU
vector.
Theorem 4.1
. Assume that ℓ
[1]
,ℓ and µ are such that
|L
2
|/q
µ
a
nd the terms of the Equations (5) and (4) are
larger than 1. Then, the iterative birthday attack on
SECRYPT 2008 - International Conference on Security and Cryptography
240

NTRU can be performed in
O ( |L
[2]
1
| · log
2
|L
[2]
1
| · d
f
/8
| {z }
W
1
+ (1+ log
2
|L
[2]
1
|
2
q
ℓ
[1]
!
) ·
|L
[2]
1
|
2
q
ℓ
[1]
| {z }
W
2
+ 1+ log
2
|L
[1]
1
|
2
q
ℓ−ℓ
[1]
!!
|L
[1]
1
|
2
q
ℓ−ℓ
[1]
| {z }
W
3
+ (log
2
|L
1
| + d
f
)
2
NGN
q
µ
|L
1
|
2
| {z }
W
4
)
(6)
vector operations, requires a memory of bit size
O ((N + (ℓ + µ)log
2
(q)) · (|L
[2]
i
| + |L
[1]
i
| + |L
i
|)) and
succeeds with probability N · 2
−ℓ
.
We get the complexity of the multiple birthday at-
tack in binary operations from Equation (6) by multi-
plying W
1
,W
2
and W
3
with N + log
2
(q) · (ℓ + µ) and
by replacing (log
2
|L
1
| + d
f
) in W
4
with log
2
|L
1
| ·
(µlog
2
(q)+ N) + d
f
·N log
2
(q). The difference of the
factors results from the different sizes of the vectors
used in each set. So far, we treated only the case,
where the term in (5) was larger than 1. However,
we can permit smaller numbers as well, which lowers
the success probability of the algorithm. Please note,
that if |L
2
|/q
µ
< 1, the number of lookups in L
2
re-
mains the same, while the number of vector additions
in the last step decreases with the expected number of
x
2
matching the x
1
.
Table 4.1 gives intuition of some parameter
choices and the expected sizes of the sets generated
during the attack.
4.2 Experimental Results
We fully implemented the attack and made variousex-
periments for small parameter sets. Our experiments
corroborate the numbers from Theorem 4.1. For the
toy example N = 53, q = 37,d
f
= 16,d
g
≈ N/2 (com-
pare (Howgrave-Graham, 2007)) our attack generated
lists of maximal 2
14
vectors, needed 2
20
vector oper-
ations and had a success probability of 1/4.
4.3 Comparison with Other Attacks
The hybrid lattice reduction/combinatorialattack pre-
sented at CRYPTO 2007(Howgrave-Graham, 2007)
by Howgrave-Graham performs a BKZ lattice reduc-
tion first and then tries to find the secret key in the
reduced lattice. Howgrave-Graham presents as well
a space-reduced variant of his attack which consists
in additional guessing of some structure in the secret
key. Table 4.2 gives an overview of the performance
of the hybrid attack (where we give the binary com-
plexity rather than the complexity in operations over
Z
q
like in (Howgrave-Graham, 2007)). We can see,
that a multiple birthday attack is competitive in mea-
sure of product of time and space. In comparison
with the space reduced variant of the hybrid attack,
the multiple birthday attack is even slightly better –
requiring about half the memory and ≈ 2
7
times less
binary operations.
Table 4.3 gives an overview over Odlyzko’s at-
tack and shows that a multiple birthday attack clearly
outperforms the standard combinatorial attack in time
and space complexity.
For a better comparison, we highlight the different
attacks for the ees251ep6 Parameter set in Table 4.4.
5 CONCLUSIONS
The iterative application of the birthday paradox to
the NTRU problem allows performing distributed
combinatorial attacks on machines with a smaller
storage capacity than previously. We achieve an at-
tack, which is about 2
7
times faster than the space-
reduced attack from (Howgrave-Graham, 2007) on
machines of about the same size (2
52
bits of mem-
ory). However, even with the achieved reduction of
the memory size we are still not able to perform com-
binatorial attacks on a Desktop PC. Therefore and be-
cause we are not able to reduce the runtime of com-
binatorial attacks, our results do not affect NTRU pa-
rameters from (P1363.1/D9, 2003) in a practical or
asymptotic sense.
5.1 Open Questions
So far were not able to combine the multiple birthday
attack presented in this paper with the hybrid attack
by Howgrave-Graham. We thus leave this question
for further research.
To better “tune” a multiple birthday attack, i.e. to
get |L
[2]
i
| ≈ |L
[1]
i
| ≈ |L
i
| ≈ |L | we propose to use re-
laxed “birthday” conditions. So far, we considered
only binary or zero birthdays, that is, we say that
two vectors x,y have a “birthday” on a position i, if
(x− y)H
i
is binary or zero. Likewise one could de-
fine birthdays as (x − y)H
i
∈ { −a,··· ,a} for some
a < q/2. We did not have time to check this, but one
A MULTIPLE BIRTHDAY ATTACK ON NTRU
241

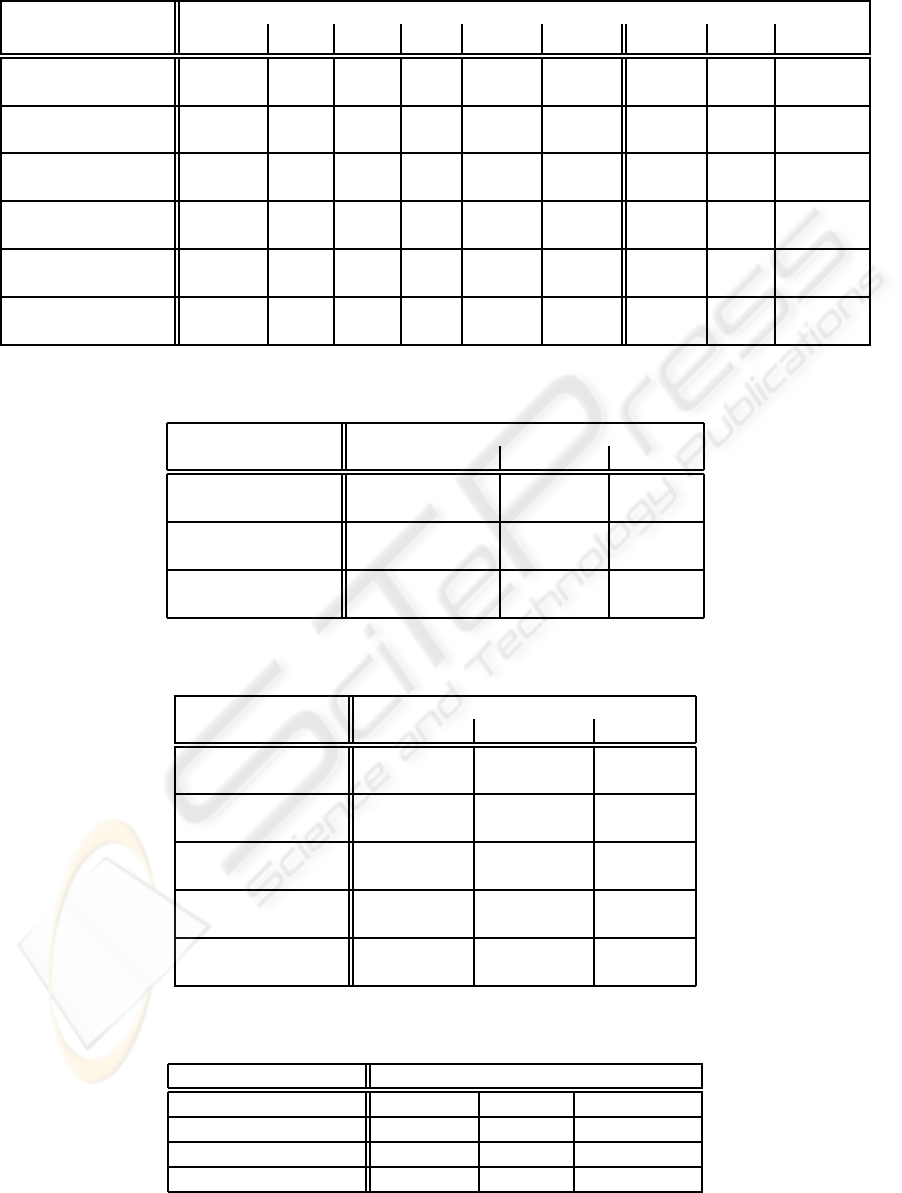
Table 4.1: The multiple birthday attack on NTRU – Time in binary operations.
NTRU Parameters Multiple Birthday attack
(N,q,d
f
,d
g
) ℓ
[1]
,ℓ,µ |L
[2]
i
| |L
[1]
i
| |L
i
| Eq. (4) Eq. (5) Eq. (6) Time Space
Toy example
(53,37,16,N/2) 1,3,3 2
10.4
2
13
2
14
2 2
−2
2
21.3
2
28
2
20.5
bits
Toy example
(107, 67,32, N/2) 2,5,5 2
22
2
26
2
31.5
2
1.5
2
−1.1
2
43.3
2
52
2
39
bits
ees251ep6
(251, 197,48, N/2) 2,8,7 2
38
2
51
2
50
2
6
2
−16
2
83.5
2
87
2
59.7
bits
ees251ep6
(251, 197,48, N/2) 3,9,7 2
38
2
43.5
2
42
2
−1.5
2
−23
2
84.2
2
90
2
52
bits
ees397ep1
(397, 307,74, N/2 4,9,14 2
69.5
2
80.6
2
83
2 2
−20
2
124
2
138.4
2
92
bits
ees491ep1
(491, 367,91, N/2) 5,14, 15 2
75
2
86.7
2
95.4
2
−0.18
2
−32
2
154
2
158
2
167
bits
Table 4.2: Performance of Howgrave-Graham’s Attack – Time in binary operations.
Parameter set Hybrid attack
(N,q,d
f
,d
g
) Space reduced Time Space
Toy example
(107, 67,32, N/2) no 2
50.6
2
36.2
bits
ees251ep6
(251, 197,48, N/2) no 2
83.8
2
65.6
bits
ees251ep6
(251, 197,48, N/2) yes 2
96.8
2
53.6
bits
Table 4.3: Odlyzko’s attack on NTRU – Time in binary operations.
Parameter set Odlyzko’s Attack
(N,q,d
f
,d
g
) # Vectors Time Space
Toy example
(53,37,16,N/2) 2
20
2
31.1
2
28.4
bits
Toy example
(107, 67,32, N/2) 2
44
2
57.3
2
53.5
bits
ees251ep6
(251, 197,48, N/2) 2
84.2
2
99.7
2
95.2
bits
ees397ep1
(397, 307,74, N/2 2
134
2
147.0
2
151
bits
ees491ep1
(491, 367,91, N/2) 2
166.5
2
184
2
178.7
bits
Table 4.4: Summary of available attacks on NTRU ees251ep6 .
Attack Time Space Time · Space
Odlyzko 2
99.7
2
95.2
bits 2
194.9
Hybrid 2
83.8
2
65.6
bits 2
149.4
Hybrid space reduced 2
96.8
2
53.6
bits 2
150.4
Multiple birthday 2
90
2
52.0
bits 2
142.0
SECRYPT 2008 - International Conference on Security and Cryptography
242

might well achieve to reduce the storage requirements
even more by this approach.
REFERENCES
Coppersmith, D. and Shamir, A. (1997). Lattice attacks
on NTRU. Proc. of Eurocrypt ’97, LNCS. Springer-
Verlag.
Hoffstein, J., Pipher, J., and Silverman, J. (1998). NTRU:
a ring based public key cryptosystem. Proc. of ANTS
III, 1423 of LNCS:267–288, Springer–Verlag.
Howgrave-Graham, N. (2007). A hybrid lattice-reduction
and meet-in-the-middle attack against ntru. In Proc.
of CRYPT’07, volume 4622 of Lecture Notes in Com-
puter Science, pages 150–169. Springer.
Howgrave-Graham, N., Nguyen, P., Pointcheval, D., Proos,
J., Silverman, J., Singer, A., and Whyte, W. (2003).
The impact of decryption failures on the security of
NTRU encryption. To appear in Proc. of CRYPTO
’03, LNCS, 2729:226–246. Springer-Verlag.
May, A. and Silverman, J. (2001). Dimension reduction
methods for convolution modular lattices. Proc. of
CaLC 2001, LNCS, 2146:111–127. Springer-Verlag.
Micciancio, D. and Goldwasser, S. (2002). Complexity of
Lattice Problems: a cryptographic perspective, vol-
ume 671 of The Kluwer International Series in En-
gineering and Computer Science. Kluwer Academic
Publishers, Boston, Massachusetts.
P1363.1/D9, I. (2003). Draft standard for public-key cryp-
tographic techniques based on hard problems over lat-
tices. W. Whyte (editor).
Silverman, J. (1999). Dimension reduced lattices, zero-
forced lattices, and the NTRU public key cryptosys-
tem. NTRU Technical Report, 013. available at
www.ntru.com.
Wagner, D. (2002). A generalized birthday problem. In
Yung, M., editor, CRYPTO, volume 2442 of Lecture
Notes in Computer Science, pages 288–303. Springer.
APPENDIX
Odlyzko’s Combinatorial Attack
Odlyzko proposed to randomly split f in two binary
parts of weight d
f
/2, say f
1
,f
2
∈ F
N
q
, such that fH =
f
1
H + f
2
H. Now, it is sufficient to list all the

⌊N/2⌋
d
f
/2

possible f
1
H
I
with f
1
of weight d
f
/2 and check for
each possible f
2
(of weight d
f
/2), if f
1
H + f
2
H is bi-
nary. Because of the possible rotations there are about
N

d
f
d
f
/2

correct choices for f
1
. By the birthday para-
dox, one correct pair f
1
,f
2
can be found after approx-
imately
s
1
N
·

N
d
f
/2

2
/

d
f
d
f
/2

(7)
samples, where each can be generated in N · d
f
/2 ad-
ditions modulo q. Here, a “collision” for the birthday
paradox is characterized by the binary sum of two
samples, which can be easily checked if the list of
samples is sorted
3
. For the ees251ep6 parameter set
from (P1363.1/D9,2003) (N = 251, q = 197, d
f
= 48,
d
g
= N/2), this attack requires storing a list of 2
84.2
vectors, compare Table 4.3.
Complexity of the Multiple Birthday
Attack with Symmetric Sets
Proof. (Theorem 4.1)
. We fist observe, that the sets
L
[2]
i
a
re the same for each i. The same holds for the
L
[1]
i
and L
i
. In the following we assume, that in each
list, we store as well the value (f·H)
{1,···,ℓ+µ}
together
with f. Computing and sorting L
[2]
i
after the lexico-
graphic order of (f, f· H)
{
1,···,ℓ
[1]
}
(most significant bit
on the right) takes
W
1
:=

N
d
f
/8

· log
2
(

N
d
f
/8

) · d
f
/8
operations on vectors in F
N
2
× F
ℓ+µ
q
. Storing these sets
requires
M
1
:=

N
d
f
/8

· (N + (ℓ + µ)log
2
(q))
bits. Generating the set(s) L
[1]
i
takes
W
2
:=

1+ log
2


N
d
f
/8

2
/q
ℓ
[1]


N
d
f
/8

2
/q
ℓ
[1]
operations, since for each element of L
[2]
2i−1
we have
about

N
d
f
/8

/q
ℓ
[1]
matching elements of L
[2]
2i
. Storing
L
[1]
i
requires
M
2
:=

N
d
f
/4

/q
ℓ
[1]
· (N + (ℓ + µ)log
2
(q))
bits. Generating the set(s) L
i
takes
W
3
:=

1+ log
2


N
d
f
/4

2
/q
ℓ−ℓ
[1]

·

N
d
f
/4

2
/q
ℓ−ℓ
[1]
operations. The resulting lists have a size of
M
3
:=

N
d
f
/2

/q
ℓ
· (N + µlog
2
(q))
3
In (Howgrave-Graham, 2007) it is proposed to use an
ordering according to the signs of the entries if f
1
H is rep-
resented as a vector with entries in the interval [−q/2,q/2].
However, other sorting criteria can be used as well.
A MULTIPLE BIRTHDAY ATTACK ON NTRU
243

bits. On the construction of L
i
we sort the lists di-
rectly after the last ℓ + µ Positions of fH. We choose
µ such that |L
i
|/q
µ
is relatively small. To find the
secret NTRU vector, for each element x
1
∈ L
1
, we
search L
2
for the elements x
2
, with a binary differ-
ence from x
1
·H in the last µ Positions, which requires
2
µ
lookups each requiring log
2
|L
2
| operations on vec-
tors in F
N
2
× F
ℓ+µ
q
plus |L
1
|/q
µ
comparisons. As soon
as we have found a binary ((x
1
+ x
2
)H)
{1,···,ℓ+µ}
, we
check that f = x
1
+ x
2
is binary and compute g = fH.
If g is binary, we have found the secret NTRU vector.
This last step requires
W
4
:=

log
2


N
d
f
/2

/q
ℓ

+ d
f

·
2
µ
q
NGN
·

N
d
f
/2

2
/q
2ℓ
operations on vectors in F
N
2
× F
N
q
. Thus, the total
workfactor for a multiple birthday attack on NTRU
starting with L
[2]
i
is
∑
4
i=1
W
i
and requires about
∑
4
i=1
M
i
bits of memory. The success probability
results from assuming g to be zero in the first ℓ
coordinates and the fact, that there are about N
different cyclic shifts of f, which can serve as secret
vector.
SECRYPT 2008 - International Conference on Security and Cryptography
244