FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2

Shinsaku Kiyomoto, Toshiaki Tanaka

KDDI R & D Laboratories Inc., 2-1-15 Ohara Fujimino-shi Saitama 356-8502, Japan

Kouichi Sakurai

Kyushu University, 744 Motooka Nishi-ku Fukuoka 819-0395, Japan

Keywords:

Stream Cipher, K2, Pseudorandom Generator, Hardware Implementation, FPGA.

Abstract:

K2 is a new type of word oriented stream cipher that has dynamic feedback control. Existing research has

shown that K2 v2.0 is a high performance stream cipher in software implementations and can be used in several

applications. However, no evaluation results for its performance in hardware implementations have been

published. In this paper, we presented two hardware implementations of K2 v2.0: a high speed implementation

and a compact implementation. We then show the evaluation results on FPGA implementation simulations.

The implementations of K2 demonstrated high efﬁciency compared with other stream ciphers, with K2 being

4-10 times higher than AES implementations. We think that the FPGA implementation of K2 is suitable for

applications using high speed encryption/decryption.

1 INTRODUCTION

Stream ciphers are used extensively to provide a re-

liable, efﬁcient method for secure communications.

A basic stream cipher uses several independent linear

feedback shift registers (LFSRs) together with non-

linear functions in order to produce a keystream. The

keystream is then XORed with plaintext to produce

a ciphertext. Recently, word-oriented stream ciphers

have been developed in order to improve the perfor-

mance of software implementations. In the NESSIE

project

, many word-oriented stream ciphers were

proposed, such as SNOW(Ekdahl and Johansson,

2000) and SOBER(Rose and Hawkes, 1999), and

demonstrated good performance in software.

The need for secure data exchange becomes im-

portant not only for high-end PCs but also low-end

customer products. Most of low-end devices require

an additional hardware implementations for encryp-

tion/decryption of transaction data. Efﬁcient hard-

ware implementations of stream ciphers are impor-

tant in both high-performanceand low-power applica-

New European Schemes for Signatures, Integrity,

and Encryption (NESSIE),

https://www.cosic.esat.

kuleuven.be/nessie/

tions. On the eSTREAM project

, many evaluation

results of hardware performances of stream ciphers

have been reported.

K2 (Kiyomoto et al., 2007b) (Kiyomoto et al.,

2007a) is a new word-oriented stream cipher us-

ing dynamic feedback control as irregular clocking.

The stream cipher has a dynamic feedback control

mechanism for the byte-level feedback function of

FSRs and realizes fast encryption/decryption for soft-

ware implementations. Several cryptographic algo-

rithms have been considered hardware implementa-

tions (Rodr´ıguez-Henr´ıquez et al., 2007). Existing re-

search has shown that K2 v2.0 is a secure and high-

performance stream cipher in software implementa-

tions and can be used in several applications. How-

ever, no evaluation results for the performance of

hardware implementations have been published. In

this paper, we presented two hardware implementa-

tions of K2 v2.0: a high speed implementation and

a compact implementation. We then show their eval-

uation results on FPGA implementations. The eval-

uation results suggested that the cipher is faster than

existing ciphers and attains a reasonable level of ef-

ECRYPT eSTREAM

http://www.ecrypt.eu.org/

stream/

270

Kiyomoto S., Tanaka T. and Sakurai K. (2008).

FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2.

In Proceedings of the International Conference on Security and Cryptography, pages 270-277

DOI: 10.5220/0001917002700277

 SciTePress

ﬁciency. We think that the FPGA implementation of

K2 is suitable for applications using high speed en-

cryption/decryption.

2 STREAM CIPHER K2 V2.0

In this section, we describe the stream cipher algo-

rithm K2 v2.0 (Kiyomoto et al., 2007a), which has a

dynamic feedback control mechanism.

2.1 Linear Feedback Shift Registers

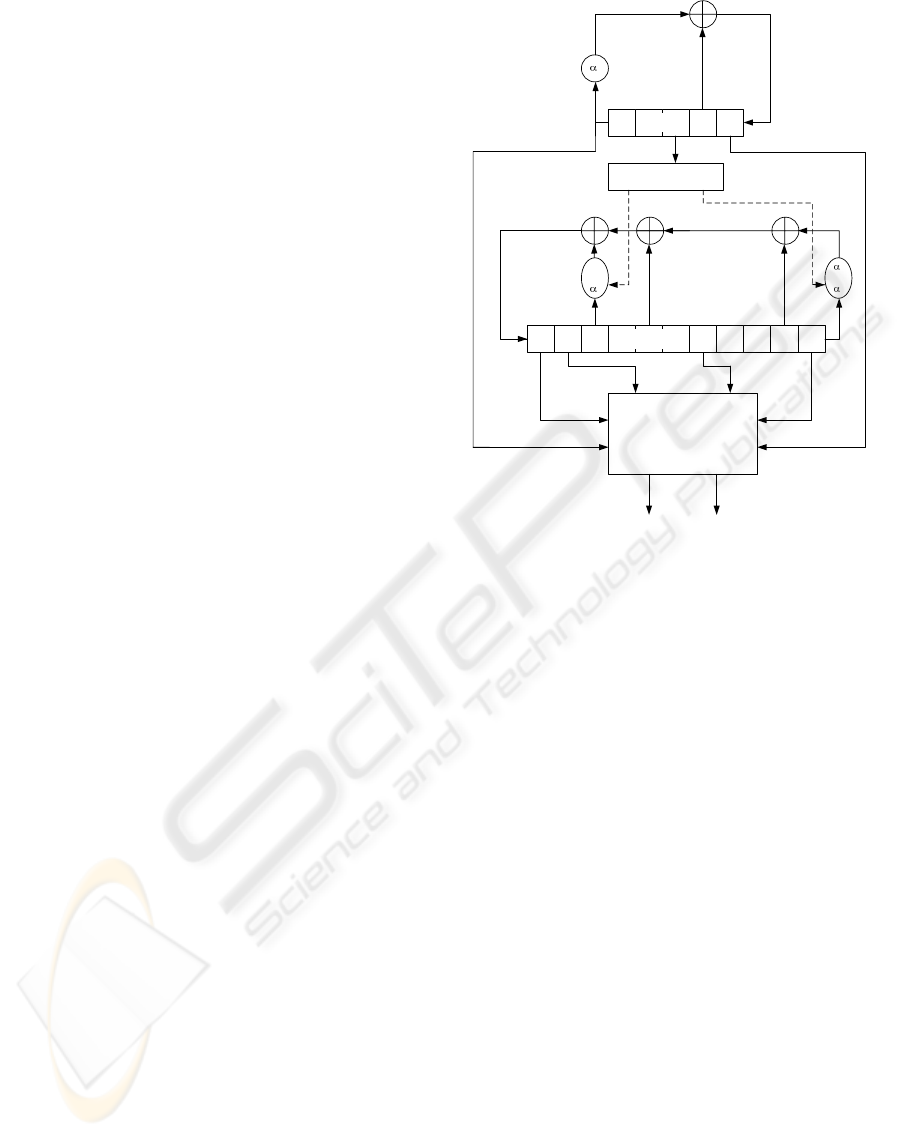
The K2 v2.0 stream cipher consists of two feedback

shift registers (FSRs), FSR-A and FSR-B, a non-linear

function with four internal registers R1, R2, L1, and

L2, and a dynamic feedback controller as shown in

Fig. 1. FSR-B is a dynamic feedback shift register.

The size of each register is 32 bits. FSR-A has ﬁve

registers, and FSR-B has eleven registers. Let β be

the roots of the primitive polynomial;

+ x

+ x+ 1 ∈ GF(2)[x]

A byte string y denotes (y

,...,y

), where y

the most signiﬁcant bit and y

is the least signiﬁcant

bit. y is represented by

y = y

+ y

+ ... + y

β+ y

In the same way, let γ, δ, ζ be the roots of the primitive

polynomials,

+ x

+ 1 ∈ GF(2)[x]

+ x

+ 1 ∈ GF(2)[x]

+ x

+ 1 ∈ GF(2)[x]

respectively.

Let α

be the root of the irreducible polynomial of

degree four

+ β

x+ β

∈ GF(2

)[x]

A 32-bit string Y denotes (Y

), where Y

a byte string and Y

is the most signiﬁcant byte. Y is

represented by

Y = Y

Let α

, α

be the roots of the irreducible polyno-

mials of degree four

+ γ

230

+ γ

156

+ γ

x+ γ

∈ GF(2

)[x]

Dynamic Feedback

Controller

FSR-B

FSR-A

Non-Linear Function

Keystream (64bits)

t+10

t+4

Figure 1: K2 v2.0 Stream Cipher.

+ δ

199

x+ δ

248

∈ GF(2

)[x]

+ ζ

157

+ ζ

253

+ ζ

x+ ζ

∈ GF(2

)[x]

respectively.

The feedback polynomials f

(x), and f

(x) of

FSR-A and FSR-B, respectively, are as follows;

(x) = α

+ x

+ 1

(x) = (α

cl1

+α

1−cl1

−1)x

+α

cl2

Let cl1 and cl2 be the sequences describing the output

of the dynamic feedback controller. The outputs at

time t are deﬁned in terms of some bits of FSR-A. Let

denote the output of FSR-A at time x, and A

[y] =

{0,1} denote the yth bit of A

, where A

[31] is the

most signiﬁcant bit of A

. Then cl1 and cl2 (called

clock control bits) are described as follows;

cl1

= A

t+2

[30], cl2

= A

t+2

[31]

Both cl1

and cl2

are binary variables; more pre-

cisely, cl1

= {0,1}, and cl2

= {0,1}. Stop-and-go

clocking is effective in terms of computational cost,

because no computation is required in the case of

0. However, the feedback function has no transfor-

mation for feedback registers with a probability 1/4

where all clockings are stop-and-go clockings. Thus,

FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2

271

we use two types of clocking for the feedback func-

tion. FSR-B is deﬁned by a primitive polynomial,

where cl2

= 0.

2.2 Nonlinear Function

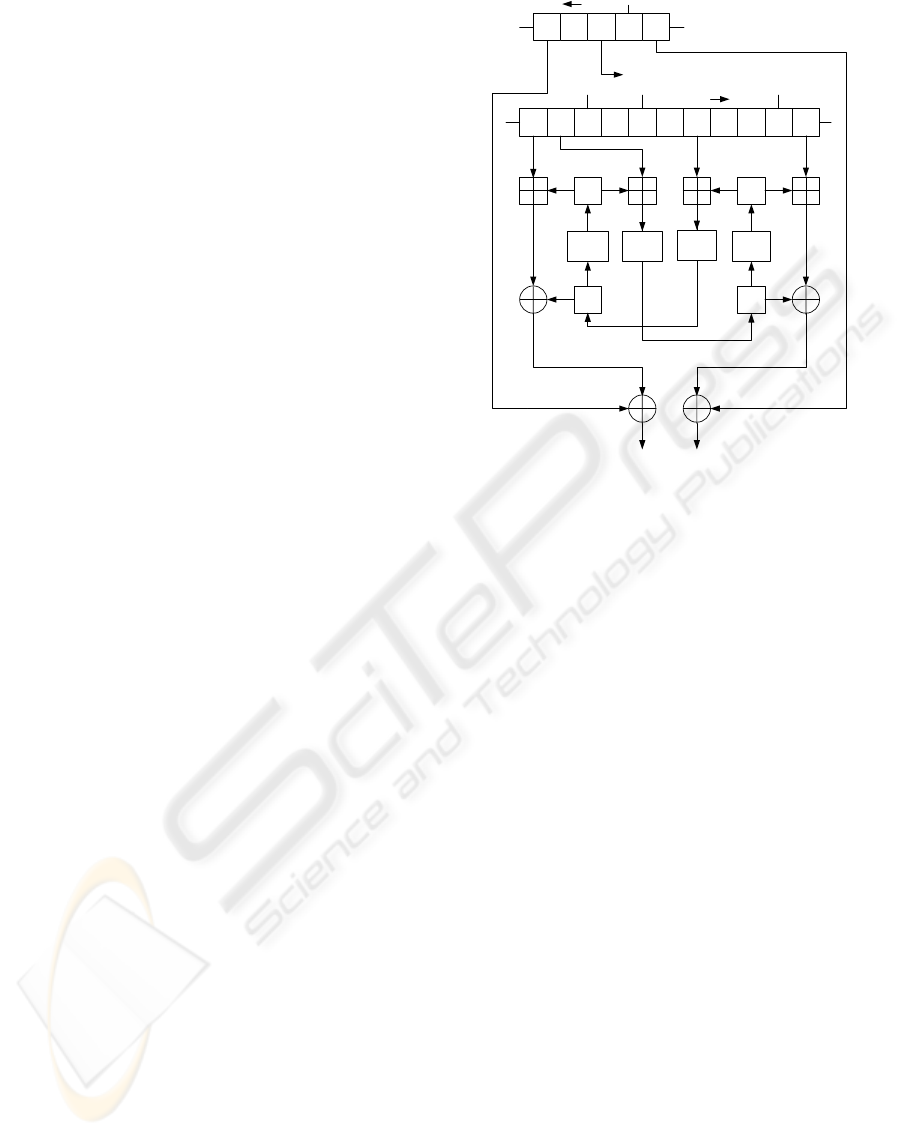
The non-linear function of K2 v2.0 is fed the values

of two registers of FSR-A and four registers of FSR-

B and that of internal registers R1, R2, L1, L2, and

outputs 64 bits of the keystream every cycle. Fig. 2

shows the non-linear function of K2 v2.0. The non-

linear function includes four substitution steps that are

indicated by Sub.

The Sub step divides the 32-bit input string into

four 1-byte strings and applies a non-linear permuta-

tion to each byte using an 8-to-8 bit substitution, and

then applies a 32-to-32 bit linear permutation. The

8-to-8 bit substitution is the same as s-boxes of AES

(Daemen and Rijmen, 1998), and the permutation is

the same as AES Mix Column operation. The 8-to-

8 bit substitution consists of two functions: g and

f. The g calculates the multiplicative inverse modulo

of the irreducible polynomial m(x) = x

+ x

x+ 1 without 0x00, and 0x00 is transformed to itself

(0x00). f is an afﬁne transformation deﬁned by;



















11111000

01111100

00111110

00011111

10001111

11000111

11100011

11110001



















⊕













where a = (a

,...,a

) is the input and b = (b

,...,b

)

is the output, and a

and b

are the least signiﬁcant bit

(LSB).

Let C be (c

) and output D be

), where c

, d

are 8-bit values. The lin-

ear permutation D = p(C) is described as follows;



















02 03 01 01

01 02 03 01

01 01 02 03

03 01 01 02



















in GF(2

) of the irreducible polynomial m(x) = x

+ x

+ x+ 1.

2.3 Keystream Output

Let keystream at time t be Z

= (z

) (each z

is a

32-bit value, and z

is a higher string). The keystream

, z

is calculated as follows:

= B

⊞ R2

⊕ R1

⊕ A

t+4

04910

FSR-B

FSR-A

Keystream (64bits)

Dynamic Feedback Controller

Sub

Figure 2: Non-Linear Function of K2 v2.0.

= B

t+10

⊞ L2

⊕ L1

⊕ A

where A

and B

denote outputs of FSR-A and FSR-

B at time x, and R1

, R2

, L1

, and L2

denote the

internal registers at time x. The symbol ⊕ denotes

bitwise exclusive-or operation and the symbol ⊞ de-

notes a 32-bit addition. Finally, the internal registers

are updated as follows;

t+1

= Sub(L2

⊞ B

t+9

), R2

t+1

= Sub(R1

)

t+1

= Sub(R2

⊞ B

t+4

), L2

t+1

= Sub(L1

)

where Sub(X) is an output of the Sub step for X.

2.4 Initialization Process

The initialization process of K2 v2.0 consists of

two steps, a key loading step and an internal state

initialization step. First, an initial internal state is

generated from a 128-bit initial key, a 192-bit initial

key, or a 256-bit initial key and a 128-bit initial

vector (IV) by using the key scheduling algorithm.

The key scheduling algorithm is similar to the round

key generation function of AES and the algorithm

extends the 128-bit initial key, the 192-bit initial

key or the 256-bit initial key to 384 bits. The key

scheduling algorithm for a 128-bit key is described as

SECRYPT 2008 - International Conference on Security and Cryptography

272











(0 ≤ i ≤ 3)

i−4

⊕ Sub((K

i−1

≪ 8) ⊕ (K

i−1

≫ 24))

⊕Rcon[i/4− 1] (i = 4n)

i−4

⊕ K

i−1

(i 6= 4n)

where IK = (IK

,IK

) is the initial key, i

is a positive integer 0 ≤ i ≤ 11, and n is a positive

integer. The function Sub(X) in the key schedul-

ing algorithm is the same as that in the non-linear

function. This function is different from the round

key generation function of AES, and the other part

of the key scheduling algorithm is the same as

the AES round key generation. Rcon[i] denotes

mod x

+ x

+ x+ 1,0x00, 0x00,0x00) and x

is 0x02. The internal state is initialized with K

and

IV = (IV

,IV

) as follows:

= K

4−m

(m = 0, ..., 4),B

= K

= IV

= K

= IV

= K

The internal registers, R1, R2, L1, and L2 are set to

0x00. After the above processes, the cipher clocks 24

times (j = 1, ..., 24), updating the internal states. The

internal states A

j+4

j+10

are also updated as follows:

j+4

=α

j− 1

⊕ A

j+2

⊕ z

j− 1

j+10

=(α

cl1

j−1

+ α

1−cl1

j−1

− 1)B

j− 1

⊕ B

j+5

⊕ α

cl2

j−1

j+7

⊕ z

j− 1

The recommended maximum number of cycles for

K2 v2.0 without re-initializing and re-keying is 2

cycles (2

keystream bits).

3 HARDWARE

IMPLEMENTATION OF K2

We considered two types of hardware implementa-

tions of K2 v2.0: a high speed implementations and a

compact size implementation.

3.1 High Speed Implementation

K2 produces a 64-bit keystream for each cycle. To

improve the performance of hardware implementa-

tions, we considered both a double-keystream and

quad-keystream implementation of hardware; the

t+1

t+2

t+3

t+4

t+5

t+6

t+7

t+8

t-1

t-2

t-3

t+3

t+2

t+1

Figure 3: Quad-Keystream Implementation of LFSR-A.

t+1

t+2

t+5

t+4

t-1

t-2

t-3

t+6

t+7

t+8

t+9

t+10

t+1

t+2

t+5

t+4

t+6

t+7

t+8

t+9

t+10

t+11

t+12

t+13

t+14

t+3

Control Bits

Figure 4: Quad-Keystream Implementation of LFSR-B.

double-keystream implementation produces a 128-bit

keystream for each clock and the quad-keystream im-

plementation produces a 256-bit keystream for each

clock. The generated keystream bits are exclusive-

ored with a plaintext/ciphertext. To implement the

double-keystream circuit, one additional register for

LFSR-A, one additional register for LFSR-B, and

four additional internal memories are required to

cache data for a double-length keystream in each cy-

cle. The quad-keystream implementation also re-

quires three registers for each LFSR, and twelve addi-

tional internal memories performed in the same man-

ner.

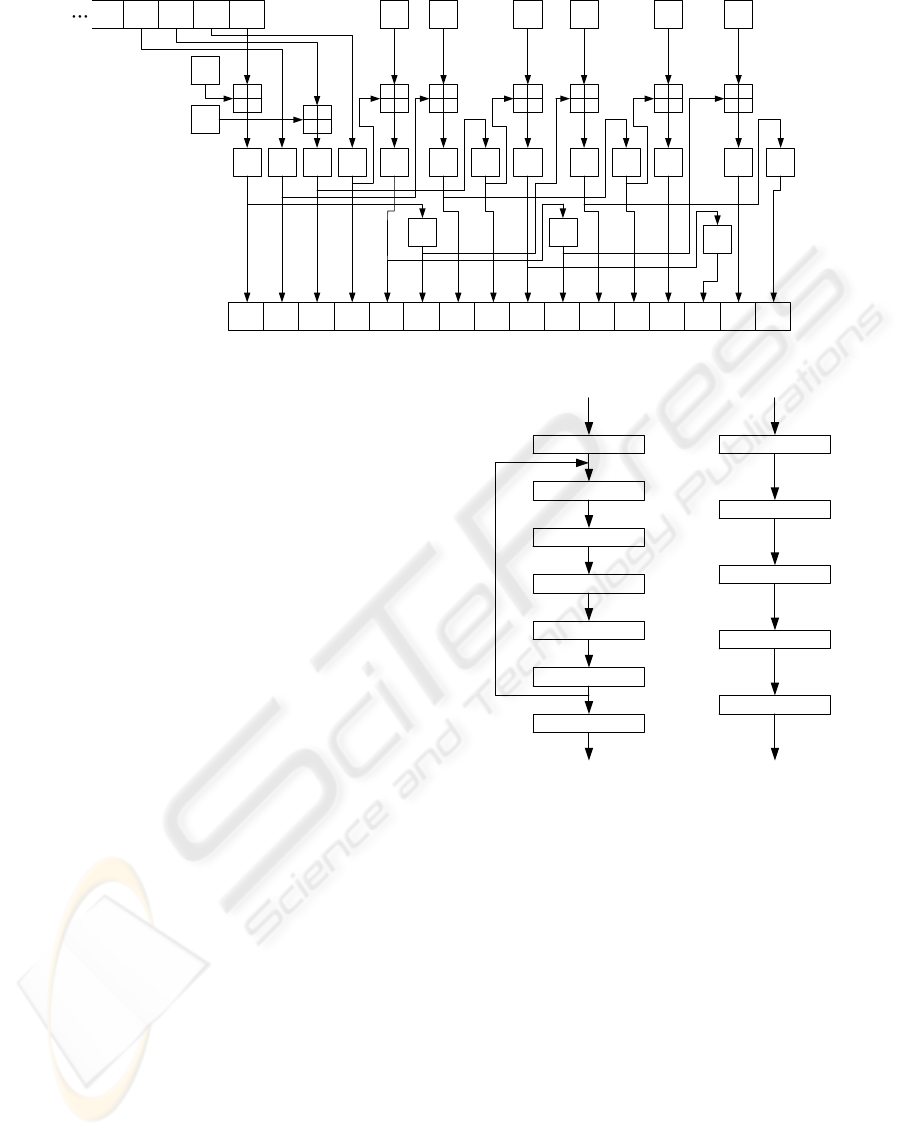
The whole circuit is parallelized using additional

circuit area, to generate double-length, quad-length

keystream per one clock cycle. Figures 3, 4, and 5

show the quad-implementation of LFSR-A, LFSR-B,

FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2

273

t+4

Sub

t+1

t+2

t+9

t+3

t+1

t+2

t+3

t+4

t-1

SubSubSub

t+5

Sub SubSub

Sub

t+10

Sub SubSub

Sub

t+11

Sub

t+6

t+7

SubSub

t+12

Sub

Figure 5: Quad-Keystream Implementation of Non-Linear Function.

and non-linear function, respectively.

The internal state values of LFSR-A, LFSR-B, and

internal memories (L1 L2 R1 R2) are updated to the

state values after four cycles by one clock cycle of the

implementation.

A 128-bit keystream Z

128

of the double-keystream

implementation for encryption/decryption is com-

puted as follows;

128

= (z

t−1

)

Similarly, a 256-bit keystream Z

256

of the quad-

keystream implementation for encryption/decryption

is computed as follows;

256

= (z

t−3

t−2

t−1

)

3.2 Compact Implementation

Rudra et. al. proposed a compact implementation

method for AES (Rudra et al., 2001). Their technique

involves mapping ﬁeld elements to a composite ﬁeld

representation. By using their technique, arithmetic

operations on GF(2

) elements are transformed into

operations in a composite ﬁeld GF((2

)

). AES op-

erations translate to the composite ﬁeld representation

as H(x) = Tx, where H denotes the mapping from

GF(2

) to GF((2

)

), and T denotes the correspond-

ing transformation matrix. That is, an 8-bit operation

in AES such as S-box is performed as 4-bit opera-

tions. Thus, the implementation size of the algorithm

can be reduced by using their techniques.

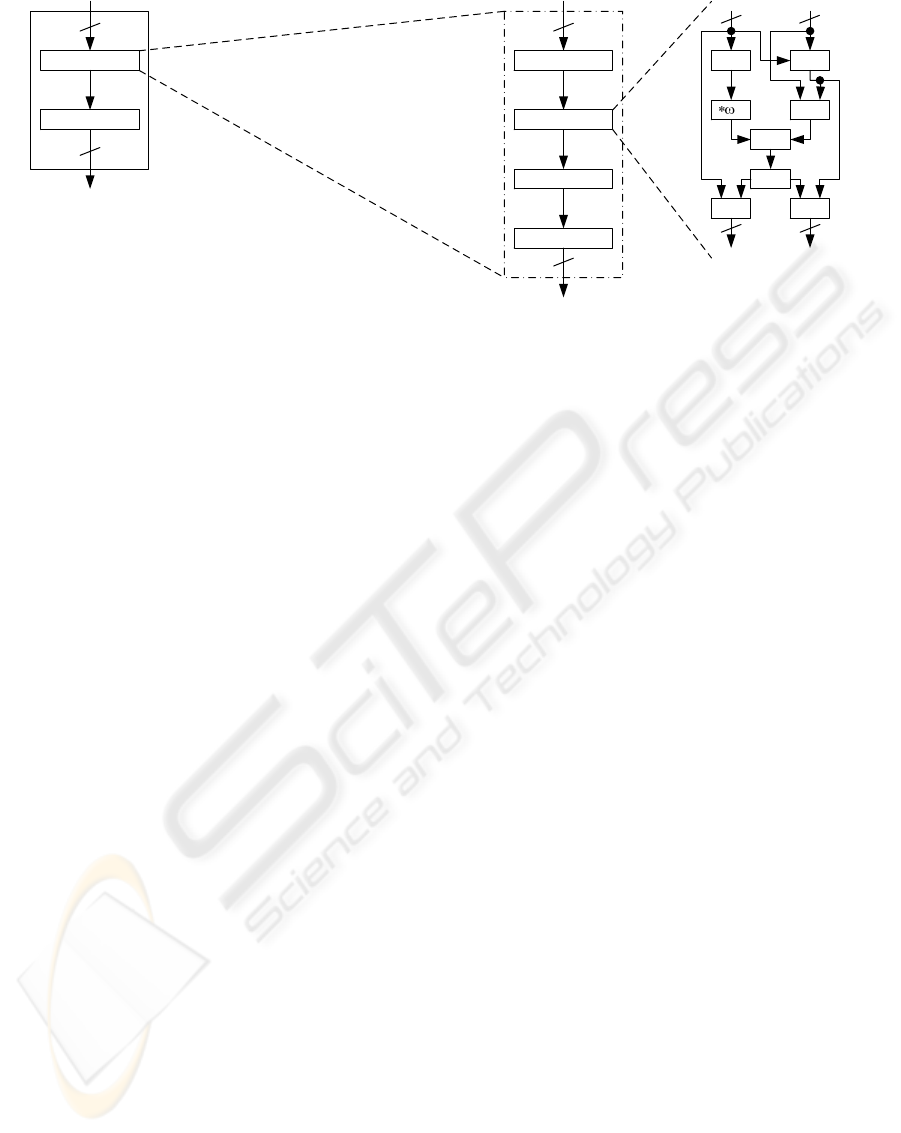
We apply their technique to a part of the non-linear

function of K2 as shown Figure 6. We add matrixes

on data paths of the substitution of K2. Input val-

ues of the inverse operations are transformed into the

elements of the composite ﬁeld by the matrix T and

Affine Trans.

-1

Inverse Calc

Mix Column

Inverse Calc

Affine Trans.

Mix Column

Shift Rows

Add Round Key

-1

΃ΦΕΣΒ͑ΖΥ͑͟ΒΝ͑͟׎Τ͑ͲͶ΄͑

ͺΞΡΝΖΞΖΟΥΒΥΚΠΟ

΀ΦΣ͑ͺΞΡΝΖΞΖΟΥΒΥΚΠΟ͑

ΗΠΣ͑ͼͣ͑Χͣ͟͡

Figure 6: Non-Linear Function Architectures Transformed

in the Composite Field.

its inverse matrix T

-1

re-transform into the elements

of GF(2

). The matrixes are an 8 × 8 transforma-

tion. Data in the inverse operation is deﬁned as an

element of the composite ﬁeld GF((2

)

), and data

out of the inverse operation is computed as an ele-

ment of GF(2

). The matrixes T and T

-1

are deﬁned

by;

T =







10100000

10101100

11010010

01110000

11000110

01010010

00001010

11011101







−1







00100100

11101110

10100100

01011010

10110010

01110010

10110000

01010001







SECRYPT 2008 - International Conference on Security and Cryptography

274

+X^2

-1

upper lower

4 4

upper lower

Inverse Calc.

Affine Trans.

;

Substitution

Mix Column

Sub

-1

Figure 7: K2 Sub Operation Architecture Transformed in the Composite Field.

The Sub consists of substitutions and the Mix Col-

umn. The substitutions involve an inverse calculation

and afﬁne transformation. We transform all inverse

operations that are located inside the substitution of

the non-linear function into inverse operations in the

composite ﬁeld. The method used for transformation

is similar to the method proposed by Rudra et. al..

They apply the method to all operations of the round

function of AES. On the other hand, we apply the

method only to the inverse operations. In AES imple-

mentations, the round function is used many times for

producing encrypted/decrypted data. However, each

Sub operation in the non-linear function are used once

for one keystream generation in K2 implementations.

Thus, the method should be applied only to inverse

operation for efﬁcient and conpact implementations

of K2. We transform the Sub that is an 8-bit oriented

operation into a 4-bit oriented operation in the com-

position ﬁeld GF((2

)

) as follows.

An inverse X

−1

of an input value X is deﬁned as;

X = r

λ+ r

, (r

∈ GF(2

))

−1

= s

λ+ s

∈ GF(2

))

where λ is a generator of GF((2

)

). In this condi-

tion, we can calculate X

−1

as follows;

= (r

+ r

)∆

−1

, s

= r

∆

−1

where ∆ = r

+ r

) + ω

and ω is a generator

of GF(2

). An inverse operation of elements x in

GF(2

) is implemented as a 4-bit-input 4-bit-output

table. The afﬁne transformation and Mix Column op-

erations are the same as the original operations of K2.

Figure 7 shows the Sub operation architecture

transformed in the composite ﬁeld. The architecture

consists of calculation units: squaring, multiplication,

addition, multiplication of ω, 4-bit inverse operation,

and exclusive-or of 4 bit values. The size of the 4-

bit inverse operation is much smaller than the size of

the 8-bit inverse operation. Thus, we can construct a

compact implementation if these calculation units are

shared by each operation and used to switch a pair of

input and output values.

4 EVALUATION RESULT

In this section, we present the evaluation results of

hardware implementations using an FPGA simula-

tor. We implemented the K2 stream cipher targeted

toward the Xilinx Spartan-II, Spartan-3, and Virtex-

II FPGAs. The circuit sizes of implementations of

normal, double-keystream, and quad-keystream im-

plementations are larger than the capacity of Spartan-

2, and thus, we evaluated normal, double, and quad-

keystream implementations on Spartan-3. We also

evaluated normal implementations on Virtex-II. The

compact implementation is evaluated on Spartan-II,

Spartan-3, and Virtex-II. We use Xilinx ISE 9.1 for

post-place and route simulation and static timing anal-

ysis.

Table 1 and Table 2 show the evaluation results

of high speed and compact implementations. Data

rate, clock frequency, throughput, and area denote the

number of bits that the cipher generates for each cy-

cle, maximum clock frequency of the circuit, maxi-

mum throughput of encryption/decryption estimated

by the maximum clock frequency, and the number of

slices of the circuit, respectively. The reduction rates

shown in Table 2 are calculated as 100× (N − M)/N,

where N is the number of slices of the normal imple-

mentation of devices and M is the number of slices

of the compact implementation for the same devices.

FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2

275

Table 1: Evaluation Results of High Speed Implementations on FPGA.

Design Data rate Clock Freq. Throughput Area Throughput/Area Device

(bits/cycle) (MHz) (Mbps) (slice) (Mbps/slice)

Normal 64 63.9 4090 3067 1.33 Spartan-3

Double-keystream 128 38.0 4864 5295 0.92 Spartan-3

Quad-keystream 256 20.4 5223 9161 0.57 Spartan-3

Normal 64 74.8 4787 2898 1.65 Virtex-II

Table 2: Evaluation Results of Compact Implementations on FPGA.

Target Data rate Clock Freq. Throughput Area Throughput/Area Reduction Rate

(bits/cycle) (MHz) (Mbps) (slice) (Mbps/slice) (%)

Spartan-II 64 30.0 1920 2133 0.90 -

Spartan-3 64 39.1 2503 2140 1.17 30.2

Virtex-II 64 48.7 3117 2145 1.45 26.0

Table 3: Comparisons with FPGA Implementations of Other Ciphers.

Algorithm Key Length Throughput Area Through./Area Normalized Device

(bit) (Mbps) (slice) (Mbps/slice) Efﬁciency

Trivium (Good et al., 2006) 80 102 40 2.55 0.80 Spartan-II

Grain (Good et al., 2006) 80 105 48 2.19 0.69 Spartan-II

Phelix (Good et al., 2006) 256 750 1077 0.70 0.70 Spartan-II

Edon80 (Kasper et al., 2006) 80 1.87 50 0.04 0.01 Spartan-3

DECIM v2 (Hwang et al., 2008) 80 46.25 80 0.58 0.18 Spartan-3

F-FCSR-H v2 (Hwang et al., 2008) 80 1104 342 3.23 1.01 Spartan-3

Pomaranch (Hwang et al., 2008) 80 49 648 0.08 0.03 Spartan-3

MICKEY-128 (Bulens et al., 2007) 128 200 190 1.05 0.53 Virtex-II

A5/1 (Galanis et al., 2004) 64 188.3 32 5.88 1.47 Virtex-II

RC4 (Galanis et al., 2004) 256 120.8 140 0.86 0.86 Virtex-II

E0 (Galanis et al., 2004) 128 189 895 0.21 0.11 Virtex-II

AES-128 (Good and Benaissa, 2005) 128 2.2 264 0.01 0.005 Spartan-II

AES-128 (Chodowiec and Gaj, 2003) 128 69 522 0.13 0.07 Spartan-II

AES-128 (Rouvroy et al., 2004) 128 87 1231 0.07 0.04 Spartan-3

AES-128 (Standaert et al., 2003) 128 1563 2257 0.69 0.35 Virtex1000

K2 Compact (this paper) 256 1920 2133 0.90 0.90 Spartan-II

K2 Normal (this paper) 256 4090 3067 1.33 1.33 Spartan-3

K2 Double− keystream (this paper) 256 4864 5295 0.92 0.92 Spartan-3

K2 Quad −keystream (this paper) 256 5223 9161 0.57 0.57 Spartan-3

We also evaluated the efﬁciency of the implementa-

tions by dividing the throughput by the area, which is

the same index used in previous studies.

The quad-keystream implementation is expected

to achieved 5 Gpbs on the Spartan-3 FPGA imple-

mentation. From the comparison of normal, double-

keystream, and quad-keystream implementations, we

showed that the rate of increase of area size is higher

than the rate of increase of throughput by using the

parallelization approach described in 3.1. The normal

implementation was shown to be the most efﬁcient

among our implementation. The compact implemen-

tation technique reduces 30.2% of slices on Spartan-

3, and 26.0% of slices on Virtex-II.

Comparisons with previously published evalua-

tion results of FPGA implementations for other ci-

phers are shown in Table 3. The column of key length

denotes a key length of each algorithm. There is a

tradeoff between the performance of the algorithm

and its security level (effective key length). Thus, we

compare an index ”Normalized Efﬁciency”. The in-

dex is calculated as (T × L)/(S × 256), where T, S,

and L denote the throughput, the area size, and the

key length respectively.

The throughput of K2 is much faster than other

block/stream ciphers, even though the circuit size is

large. In terms of efﬁciency, the implementations of

K2 has high efﬁciency when compared with other

stream ciphers, and is 4-10 times higher than AES

implementations. The FPGA implementation of K2

is suitable for applications that require high speed en-

cryption/decryption and accepts medium size circuits

for hardware implementations.

SECRYPT 2008 - International Conference on Security and Cryptography

276

5 CONCLUSIONS

This paper presented the evaluation results of sev-

eral FPGA implementations of K2 v2.0: high

speed implementations and compact implementa-

tions. The quad-keystream implementation is ex-

pected to achieved 5 Gbps on a Spartan-3 FPGA im-

plementation, and the circuit size of the compact im-

plementation of K2 is 2133 on Spartan-II. Further-

more, we evaluated the efﬁciency of the implementa-

tions using two benchmarks: throughput per area and

the normalized efﬁciency. The implementationsof K2

has high efﬁciency compared with other stream ci-

phers, and its efﬁciency is 4-10 times higher than AES

implementations. The evaluation results suggested

that the FPGA implementation of K2 is suitable for

applications using high speed encryption/decryption.

REFERENCES

Bulens, P., Kalach, K., Standaetes, F. X., and Quisquater,

J. J. (2007). FPGA implementations of estream phase-

2 focus candidates with hardware proﬁle. In SASC

2007 Workshop Record, pages 205–214. eSTREAM

Project.

Chodowiec, P. and Gaj, K. (2003). Very compact FPGA

implementation of the AES algorithm. In Proc.

of CHES’03, LNCS, volume 2779, pages 319–333.

Springer Verlag.

Daemen, J. and Rijmen, V. (1998). The Design of Rijn-

dael, Information Security and Cryptography, Texts

and Monographs. Springer Verlag.

Ekdahl, P. and Johansson, T. (2000). SNOW -a new stream

cipher. The NESSIE submission paper.

Galanis, M. D., Kitsos, P., Kostopoulos, G., and

Koufopavlou, O. (2004). Comparison of the perfor-

mance of stream ciphers for wireless communications.

In Proc. of CCCT’04, pages 113–118.

Good, M. and Benaissa, M. (2005). AES on FPGA from the

fastest to the smallest. In Proc. of CHES’05, LNCS,

volume 3659, pages 427–440. Springer Verlag.

Good, T., Chelton, W., and Benaissa, M. (2006). Review

of stream cipher candidates from a low resource hard-

ware perspective. In SASC 2006 Workshop Record.

eSTREAM Project.

Hwang, D., Chaney, M., Karanam, S., Ton, N., and Gaj,

K. (2008). Comparison of FPGA-targeted hardware

implementations of eSTREAM stream cipher candi-

dates. In SASC 2008 Workshop Record, pages 151–

162. eSTREAM Project.

Kasper, M., Kumar, S., Lemke-Rust, K., and Paar, C.

(2006). A compact implementation of edon80. eS-

TREAM Report 2006/057.

Kiyomoto, S., Tanaka, T., and Sakurai, K. (2007a). K2: A

stream cipher algorithm using dynamic feedback con-

trol. In Proc. of SECRYPT 2007, pages 204–213. IN-

STICC PRESS.

Kiyomoto, S., Tanaka, T., and Sakurai, K. (2007b). A word-

oriented stream cipher using clock control. In SASC

2007 Workshop Record, pages 260–274. eSTREAM

Project.

Rodr´ıguez-Henr´ıquez, F., Saqib, N. A., D´ıaz-Perez, A., and

Koc, C. K. (2007). Cryptographic algorithms on re-

conﬁgurable hardware. Signals and Communication

Technology, Springer.

Rose, G. and Hawkes, P. (1999). The t-class of SOBER

stream cipher. Publication Document, QUALCOMM

Australia.

Rouvroy, G., Standaert, F. X., Quisquater, J. J., and

Legat, J. D. (2004). Compact and efﬁcient encryp-

tion/decryption module for FPGA implementation of

the AES Rijndael very well suited for small embedded

applications. In Proc. of ITCC 2004, volume 2, pages

583–587.

Rudra, A., Dubey, P. K., Julta, C. S., Kumar, V., Rao, J. R.,

and Rohatgi, P. (2001). Efﬁcient rijndael encryption

implementation with composite ﬁeld arithmetic. In

Proc. of CHES’01, LNCS, volume 2162, pages 171–

184. Springer Verlag.

Standaert, F. X., Rouvroy, G., Quisquater, J.-J., and Legat,

J.-D. (2003). Efﬁcient implementation of rijndael en-

cryption in reconﬁqurable hardware: Improvements

and design tradeoffs. In Proc. of CHES’03, LNCS,

volume 2779, pages 334–350. Springer Verlag.

FPGA-TARGETED HARDWARE IMPLEMENTATIONS OF K2

277