
AN EFFICIENT RECONFIGURABLE SOS MONTGOMERY
MULTIPLIER IN GF
(P) USIGN FPGA DSP SLICES
Muhammed Nauman Qureshi, Muhammad Nadeem Sial
National University of Science and Technology, Islamabad, Pakistan
Nassar Ikram
National University of Science and Technology, Islamabad, Pakistan
Keywords: Montgomery Modular Multiplication (MMM), Separated Operand Scanning (SOS), Field Programmable
Gate Arrays (FPGA), Public Key Cryptography, Elliptic Curve Cryptography (ECC), RSA.
Abstract: Montgomery Modular Multiplication in hardware is of great importance for the realisation of practical
public key systems. Hence, an efficient implementation of modular exponentiation in terms of speed and
resources in hardware is essential. This paper focuses on implementation of fully pipelined SOS based
Montgomery Multiplication algorithm in Virtex-5 FPGA using DSP slices to achieve best area-speed trade
off. Our implementation results and comparison with other Multipliers show that our Multiplier is
comparable to known Montgomery Multipliers in terms of area-speed trade off.
1 INTRODUCTION
In public key cryptosystems i.e. ECC & RSA,
arithmetic operations, modular exponentiation and
Modular Multiplication are of crucial importance for
the performance of the system. Montgomery
Multiplication is an efficient method to perform
Modular Multiplication introduced by Peter L.
Montgomery (1985). An overview of different
algorithms for Montgomery Modular Multiplication
(MMM) using a single b-bit integer multiplier is
given by Koc (1996).
In this paper, hardware architecture for improved
SOS based MMM in FPGA using dedicated
multiplier block to achieve speed and area trade off
is presented. We used Virtex-5 DSP48E Slices for
practical realization of basic step of SOS i.e. 32x32
bits multiplier and full length adder.
The remainder of the paper is organized as
follows. Section 2 introduces the Montgomery’s
Algorithm. Section 3 gives a summary of previous
work. Section 4 presents detailed description of our
Multiplier. Section 5 presents the implementation
results with comparisons made to the known
implementations. Section 6 concludes the paper.
2 MONTGOMERY
MULTIPLICATION
Montgomery Multiplication is the most popular and
efficient method to perform Modular Multiplication.
It was introduced by Peter L. Montgomery (1985)
and presented as Algorithm 1 in this paper.
Algorithm 1: Montgomery Modular Multiplication
Require:
N
= (
N
n−1 . . .N0) 2
b
, A = (An−1 . . .A0)
2
b
, B = (Bn−1 . . . B0) 2
b
with 0 ≤ A, B < N, R =
2
n.b
, gcd(N, 2
b
) = 1 and N′ = −N
-1
mod 2
b
Ensure: (A·B·R
-1
) mod N
1: T = (Tn . . . T0) 2
b
← 0
2: for i from 0 to n − 1 do
3: Ui ← ((T0 + A0·Bi) ·N′) mod 2
b
4: T ← (T+A·Bi +N·Ui)/ 2
b
5: end for
6: if T ≥ N then
7: T ← T − N
8: end if
9: Return T
Koc (1996) presented an overview of different
algorithms for Montgomery Multiplication using a
single b-bit integer multiplier. The algorithms are
SOS, CIOS, FIOS, FIPS and CIHS. Walter (1999 &
Oct, 1999) presents an improved MMM algorithm
355
Nauman Qureshi M., Nadeem Sial M. and Ikram N. (2008).
AN EFFICIENT RECONFIGURABLE SOS MONTGOMERY MULTIPLIER IN GF (P) USIGN FPGA DSP SLICES.
In Proceedings of the International Conference on Security and Cryptography, pages 355-358
DOI: 10.5220/0001917303550358
Copyright
c
SciTePress

that performs an extra iteration which results in the
avoidance of the conditional final subtraction. Our
work is targeted towards fully pipelined
implementation of improved SOS algorithm only.
3 PREVIOUS WORK
There exists a substantial amount of previous work
on the implementation of Montgomery Multipliers.
In this section, the most important known
Montgomery Multipliers implementation over GF(P)
in FPGAs have been discussed.
A scalable systolic array was implemented by
Batina (2004). Manochehri (2004) introduced
pipelining inside the CSA logic. McIvor (2004) gave
a comparison of the algorithms presented by Koc
(1996). Bunimov (2002) designed Montgomery
Multipliers by using carry-save adders and practical
FPGA implementation of this design is given by
Amanor (2005). Kelley (2005) designed a scalable
Montgomery Multiplier by using two w·v-bit
multipliers, two 3-2 carry-save adders and one w+v
carry-propagate adder. Nele Mentens (July, 2007)
gave parallel implementation of algorithms
presented by Koc (1996) and claims to be the fastest
published Montgomery Multiplier on FPGA.
4 OUR SOS MULTIPLIER
We focused on implementation of improved SOS
based Montgomery algorithm by using Virtex-5
DSP48E slices. We designed the basic 32x32 bit
multiplier and 32 bit adders in DSP48E (UG193,
April, 2006). Complete 1024 bits SOS based
Montgomery Multiplier was implemented by
adopting pipelined architecture employing dual port
RAMs.
4.1 Design Realization
The hardware realization of improved SOS
algorithm has been shown in Figure 1. In Step 1, we
multiply each 32 bit word of 2
nd
variable B with the
complete 1056 bits words of 1
st
variable A. The
multiplication output is 2*b bits which is represented
as C and S, where C is the upper b bit word and S is
the lower one. The C word is delayed by one clock
cycle and added with the next S word computed. In
this manner we get n*b bit words of T as shown in
Figure 1.
In order to form the complete T, we shift the first
computation (B
0
*A) by one word after extracting the
T
0
word and add with the second n*b bit words
computed from B
1
*A as shown in the Figure 1. It is
worth noting that the value of “m” required in step 2
is computed in parallel as soon as T
0
becomes
available.
B
A
T
..........................................................................
............
<< & +
<< & +
<< & +
T
T
X
+
T
T
Last Carry
X
X
+
X
+
Discard
+
T
Last Carry
x
i = 0
i = 1
+
+
+
+
+
ADD Function
+
+
T
H
+
ADD Function
+
+
Discard
Answer will accumulate in the T
H
Step 2
Step 1
T
H
T
H
Step 2 continues till the last word of T
L
A
i+1
A
i
C
SB
i
C
i
T
0
T
i+1
T
i+2
T
i
T
i+1
T
i+2
T
i
T
i+1
T
i+2
T
0
T
i+1
T
i+2
T
i+5
T
i+6
T
i+7
T
0
T
L
T
H
C
S
m
0
N'
N
0
N
C
i
T
0
T
1
T
2
C
S
m
1
N'
N
0
N
C
i
T
1
T
2
T
2
T
H0
Figure 1: Hardware Flow of Algorithm.
In Step 2 we have to perform two types of
iterations. In the first iteration, we compute new T
by multiplying “m” with N
j
and add the old T values
to it. The result is a 2*b bit word formed as C and S
as in step 1. C is added to the result as in the
previous step. However the major differences
between this step and the previous one are:-
Instead of Shift and Add operation in step 1,
ADD Function (Refer Figure 1) is performed.
It is carried out upon completion of
multiplication operation on n lower words of T
(i.e. T
L
). The ADD function simply adds the
carry (C
i
) generated from (T
n
+m
i
*N
n
) words.
In hardware, we have implemented it
independently.
The computation of m
i
for each step is done as
soon as the T
i
word in T
L
has been computed.
A dedicated Multiplier computes this result in
hardware.
SECRYPT 2008 - International Conference on Security and Cryptography
356
A
.
.
B
B
1
.
.
.
A
1
A
0
M
32 bits
A
i
32
32
32
32
32
32
Mu x
C
C
Mu x
Mu x
Mu x
B
i
S
.
.
B
0
.
N
Mu x
T
i
32 bits
Mu x
T
i
U
i
32 Bit
Register
Only Used in Step 2
DSP48E
Based
32x32
Multiplier &
Full Adder
32x32 bit
C Adder
32 X32
bit
m
Modular
Multiplier
32x32 bit
T
i
Adder
B
32
B
33
A
32
A
33
Legend
32 Bit
Store
Register
32 Bit
Store
Register
m
i
carry
i
32 bits
32 bits
32 bits
N
/
.
.
.
.
N
0
N
1
N
32
N
33
32x33 bits
Dual Port
T
L
RAM
32x33 bits
Dual Port
T
H
RAM
32X32
Shift
Register
32x33 RAM
32x33 RAM
32x33 RAM
Figure 3: Architecture of fully pipelined 1024 bits SOS Based Montgomery Multiplier.
Because of the parallel processing of ADD
function and computation of “m”, a lot of clock
cycles are saved, and the main state machine only
concerns with computation of T with N.
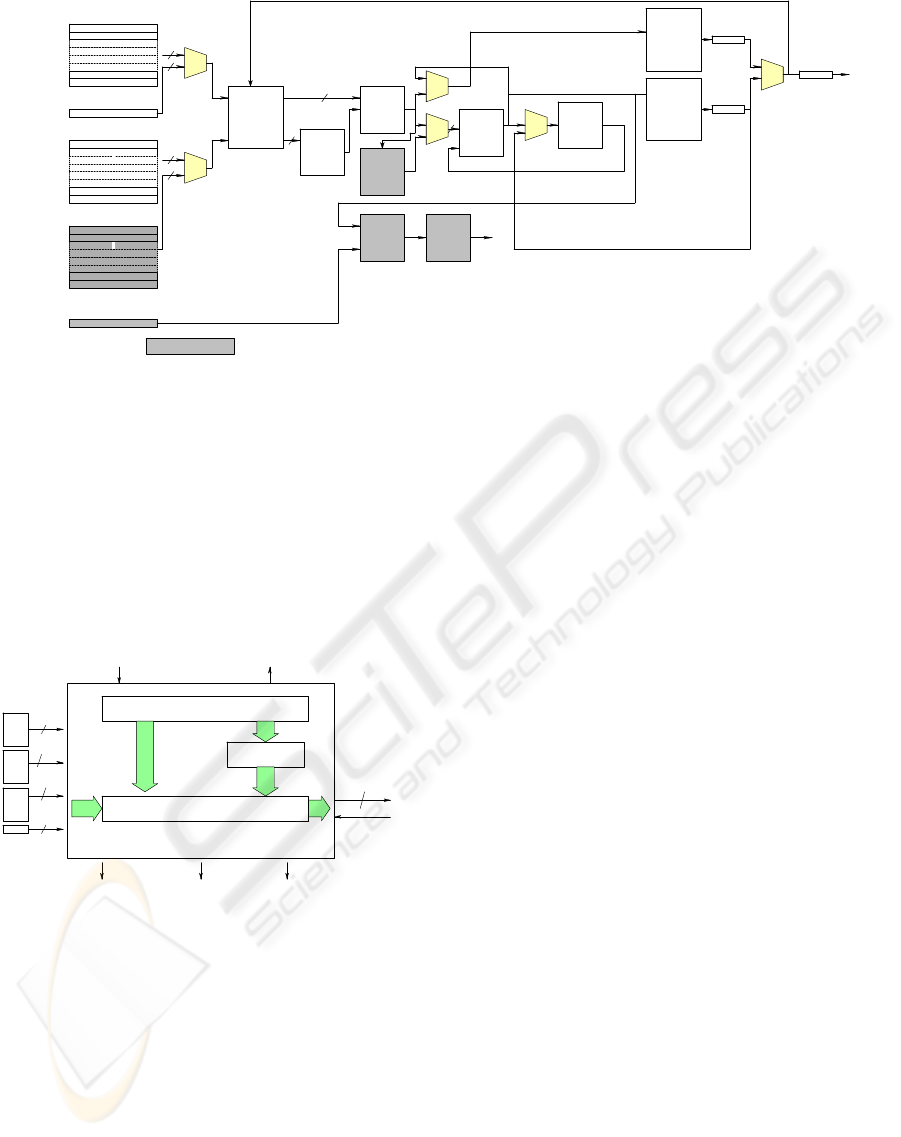
4.2 Top Level Design
The Top level design of the Multiplier is given in
Figure 2.
Main Controller
Pipeline
Delay
Inputs Outputs
Add N
Add B
Add A
State
State
32 bits
32 bits
32 bits
A
i
B
i
N
i
Reg
Ready
Add T
32 bits
32 bits
N
/
T
N
32X33
RAM
B
32X33
RAM
A
32X33
RAM
Mult
1024 bits SOS
Montgomery Modular Multiplier
Fully Pipelined 1024 bits Improved SOS MMM
Figure 2: Top Level Pictorial Diagram.
4.3 1024 Bit Multiplier Architecture
Figure 3 presents the hardware architecture of 1024
bit SOS Montgomery Modular Multiplier.
Components used for Step 2 in addition to Step1 are
shown in shaded pattern.
Majority of the components used in the
Multiplier are Xilinx Cores. 32x32 bit Multiplier
with 32 bit Adder is implemented using the fully
pipelined Multiplier architecture (Xilinx Virtex-4
Handbook, 2004).
5 IMPLEMENTATION RESULTS
& COMPARISION
Table 1 gives the implementation results for our
Montgomery Multiplier. The final design was
implemented at a speed of 269.5
MHz. Total clock
cycles comes out to be [(2b*(b+1))+ 23]. Time in
case of 1024 bits multiplication is more as compared
to Mentens (2007)
& Kelley (2005) because of
greater number of cycles required for each
computation. This could be improved if 64x64 bit
Multiplier is implemented using our design which
happens to be our current pursuit.
A comparison between Koc (1996)
, McIvor (2003),
Mentens (2007), Kelley (2005), McIvor (2004) and
our implementation is also presented in Table 1.
Especially the comparison to the Montgomery
Multiplier presented by Mentens (2007) is important
(Table 1, shown in shaded pattern), because it claims
to be the fastest published Montgomery Multiplier
on FPGA. Results of Mentens (2007) exhibit speed
merits of implementation but at the cost of extensive
resource utilization. Kelley (2005), shows that the
implementation achieves the best area and speed
trade off (Table 1, shown in shaded pattern).
Although direct comparison to Kelley (2005), in
terms of resource utilization is harder to evaluate,
but our Multiplier is comparable to it in terms of
area and speed which is our main objective.
AN EFFICIENT RECONFIGURABLE SOS MONTGOMERY MULTIPLIER IN GF (P) USIGN FPGA DSP SLICES
357

Table 1: Implementation results, resource utilization and speed comparison.
Ref Freq
MHz
Resources Timing (µs) FPGA
160 256 512 1024
Our 269.5 9 DSP Slices+558 Slices 0.39 0.75 2.35 8.41 XC5VLX50T
Mentens (2007)
108 66 MULTs+8192 Slices+66 RAM
Blocs
0.89 1.28 2.33 4.4 XC2VP30
Mentens (2007)
87 68 MULTs+7944 Slices 0.30 0.46 - 1.62 XC2VP30
Mentens (2007)
152 36 MULTs+6650 Slices 0.34 0.53 - 1.82 XC2VP30
McIvor (2004)
76 64 MULTs+4663 Slices - 1.22 - - XC2VP125
McIvor (2003)
76 11617 Slices - - - 13.11 XC2V3000
Kelley (2005)
135 32 MULTs+2593 LUTs+5K RAM - 0.39 - 2.4 XC2V2000
Kelley (2005)
135 8 MULTs+695 LUTs+5K RAM - 0.68 - 8.3 XC2V2000
Koc (1996)
60 Not Applicable - - - 799 Pentium-60
6 CONCLUSIONS
This paper presented the design methodology for
implementing improved SOS MMM for large
integers GF(P) of 32 bit word size in FPGAs using
DSP Slices to achieve area and speed trade off.
The proposed SOS Montgomery Multiplier was
implemented and tested at 269.5MHz with 160, 256,
512 and 1024 bit integers.
The fundamental contribution of this work is to
show that it is possible to design efficient
Montgomery Multipliers without compromising
scalability, portability, time performance and area
efficiency. Our multiplier is comparable to known
Montgomery Multipliers in terms of area-speed
trade off.
REFERENCES
P., Montgomery, 1985. Modular multiplication without
trial division. Mathematics of Computation. vol. 44,
no. 170, pp.519–521.
C.¸ K., Koc, T., Acar, and B., S., Kaliski, 1996. Analyzing
and comparing Montgomery multiplication
algorithms. IEEE Micro. vol. 16, no. 3, pp. 26-33.
C., D., Walter, October 1999. Montgomery exponentiation
needs no final subtraction. Electronic letters. vol. 35,
no. 21, pp. 1831–1832.
C., D., Walter, 1999. Montgomery’s multiplication
technique: How to make it smaller and faster. In C.¸
K., Koc and C., Paar, editors, Proceedings of the 1st
International Workshop on Cryptographic Hardware
and Embedded Systems (CHES), Lecture Notes in
Computer Science, Springer-Verlag. no. 1717, pp. 80–93.
Virtex-5 XtremeDSP Design Considerations User Guide,
April 14, 2006. V1.0, UG193, www.xilinx.com.
C., McIvor, M., McLoone, J., V., McCanny, A., Daly, and
W., Marnane, 2003. Fast Montgomery modular
multiplication and RSA cryptographic processor
architectures. In Proceedings of the 37th Annual
Asilomar Conference on Signals, Systems and
Computers. pp. 379–384.
Nele., Mentens, July, 2007. Secure and Efficient
Coprocessor Design for Cryptographic Applications
on FPGAs. PhD thesis. ISBN 978-90-5682-843-1.
K., Kelley and D., Harris, 2005. Parallelized very high
radix scalable Montgomery multipliers. In Conference
Record of the Thirty-Ninth Asilomar Conference on
Signals, Systems and Computers. pp. 1196–1200.
C., McIvor, M., McLoone, and J., V., McCanny, 2004.
FPGA Montgomery multiplier architectures – a
comparison. In Proceedings of the 12th IEEE
Symposium on Field-Programmable Custom
Computing Machines (FCCM), IEEE Computer
Society. pp. 279–282.
K., Manochehri and S., Pourmozafari, 2004. Fast
montgomery modular multiplication by pipelined CSA
architecture. In Proceedings of the International
Conference on Microelectronics (ICM). pp. 144–147.
D., N., Amanor, V., Bunimov, C., Paar, J., Pelzl, and M.,
Schimmler, 2005. Efficient hardware architectures for
modular multiplication on FPGAs. In Proceedings of
the 15th International Conference on Field
Programmable Logic and Applications (FPL), IEEE.
pp. 539–542.
V., Bunimov, M., Schimmler, and B., Tolg, 2002. A
complexity-effective version of Montgomery’s
algorithm. In Proceedings of the Workshop on
Complexity Effective Designs (WCED).
L., Batina, G., Bruin-Muurling, and S., B., Ors, 2004.
Flexible hardware design for RSA and elliptic curve
cryptosystems. In T. Okamoto, editor, Proceedings of
the RSA Conference – Topics in Cryptography (CT-
RSA), Lecture Notes in Computer Science Springer-
Verlag. vol. 2964, pp. 250–263.
Xilinx Virtex-4 Handbook. August 2, 2004.
SECRYPT 2008 - International Conference on Security and Cryptography
358
