A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS

Mohamed Abo El-Fotouh and Klaus Diepold

Institute for Data Processing (LDV), Technische Universit

at M

unchen (TUM), 80333 M

unchen, Germany

Keywords:

High-speed networks, encryption schemes, SSM, AES.

Abstract:

In this paper we studied the two widely used encryption schemes to perform symmetric encryption for a

huge number of concurrent clients in high-speed networks applications. The current schemes consume either

plenty of memory to gain high throughput or low memory with low throughput. The need has aroused for

a scheme that has low memory requirements and in the same time possesses high speed, as the number of

the internet users increases each day. We used the SSM model (El-Fotouh and Diepold, 2008), to construct

an encryption scheme based on the AES. The proposed scheme possesses high throughput together with low

memory requirements. We performed theoretical and practical analyses for the existing and proposed schemes.

1 INTRODUCTION

The number of internet users is increasing continu-

ally world wide. Recent statistics reported the cur-

rent number of internet users is more than 1.24 bil-

lion. This number has increased more than 290 % in

the last seven years and is still increasing daily (Stats,

2008). Consequently, internet and network applica-

tions need to serve an increasing number of concur-

rent clients. The enhanced quality and performance of

internet and modern applications require more band-

width capacity to fullﬁll the clients’ needs. Today,

modern networks do not only have to fulﬁll the de-

mand of higher transmission rates but also have to

provide and to guarantee data security and especially

data conﬁdentiality (Jung et al., 2001).

The encryption and decryption key setup laten-

cies are particularly important in applications where

only several blocks of data are encrypted between two

consecutive key changes. IPSec (Kent and Atkinson,

1998a; Kent and Atkinson, 1998b; Kent and Atkin-

son, 1998c) and ATM (Dunn and Martin, 2000), with

small sizes of packets, and consecutive packets en-

crypted using different keys, are two widespread pro-

tocols in which the key setup latencies may play a

very important role (Gaj and Chodowiec, 1999).

Ciphers that require subkeys pre-computation

have a lower key agility due to the pre-computation

time, and they also require extra RAM to hold the

pre-computed subkeys. This RAM requirement does

not exist in the implementations of encryption algo-

rithms, which compute their subkeys during the en-

cryption/decryption operation ”on-the-ﬂy” (Sklavos

et al., 2005).

On October 2, 2000 the National Institute of Stan-

dards and Technology (NIST) announced that Rijn-

dael (Daemen and Rijmen, 1998) has been chosen

to become the Advanced Encryption Standard (AES)

and it was announced as a standard in (NIST, 2001).

Rijndael supports on-the-ﬂy subkeys computation for

encryption, but it requires a onetime execution of the

key schedule to generate all subkeys prior to the ﬁrst

decryption with a speciﬁc key. This places a slight re-

source burden on the key agility of Rijndael (Schneier

et al., ).

In this paper, we studied the two widely used

schemes for generating the cipher’s subkeys in net-

work applications. The ﬁrst scheme uses subkeys

pre-computation and the second uses on-the-ﬂy sub-

keys computation. We performed theoretical and ex-

perimental analyses on both schemes. Our analy-

ses pointed out some shortcomes in both schemes,

as the scheme that uses on-the-ﬂy subkeys computa-

tion is considered slow, on the other hand the scheme

that uses subkeys pre-computation uses more mem-

ory, which may limit the number of concurrent clients

and is more subjected to cache misses and page faults.

To overcome the shortcomes of both schemes, we

proposed a new scheme. Our scheme is based on

the Static Substitution Model (SSM) (El-Fotouh and

119

Abo El-Fotouh M. and Diepold K. (2008).

A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS.

In Proceedings of the International Conference on Security and Cryptography, pages 119-127

DOI: 10.5220/0001919101190127

 SciTePress

Diepold, 2008). The SSM model can provide a block

cipher with a secondary key. The secondary key is

used to replace some bits of the cipher’s expanded

key. We used the SSM model to construct a variant

of the AES, we named this variant AESS. We used

AESS to construct an encryption scheme for network

applications. In the proposed scheme, each client pos-

sesses two keys. The ﬁrst key is shared with a group

of clients (a cluster) and it is expanded in memory

(cluster key). The second key is the client’s unique

session key. Encryption and decryption are done us-

ing AESS, where the cluster key is used as the ex-

panded AES key and the client’s session key is used

as the secondary key. Our proposed scheme enjoys

high throughput together with low memory consump-

tion.

This paper is structured as follows. In section 2 we

present the current encryption schemes together with

our general assumptions. In section 3 we propose a

variant of the AES and present our proposed encryp-

tion scheme for networks applications. In section 4

we present the memory analysis of the schemes. In

section 5 present a simulation to help us better un-

derstand the behavior of the schemes in real systems.

In section 6 we present the security analysis of the

schemes. We conclude in section 7.

2 CURRENT SCHEMES

2.1 General Assumptions

Assumptions:

1. We have a Server that serves N (large/huge num-

ber) of concurrent secure sessions.

2. Each client has a unique random session key of

size 256-bits and a unique random initial vector

(IV) of size 128-bits. .

3. We are going to use the AES (with 256-bits key)

for encryption and decryption.

4. For decryption, we are going to use the Equiva-

lent Inverse Cipher of AES (Daemen and Rijmen,

1998), that has the same sequence of transforma-

tions as AES, thus offers a more efﬁcient structure

than the normal Inverse Cipher (NIST, 2001) and

is used in many optimized software and hardware

systems (Gladman, 2006; Lai et al., 2004; Li and

Li, 2005; Tillich and Groschdl, 2006).

5. The encryption/decryption is done in CBC

mode (Menezes et al., 1996), which is used

by most network applications (Tan et al., 2004;

Walker, 2000).

2.2 Scheme 1

Scheme 1 is a speed dedicated scheme, where the ex-

panded key for encryption and decryption for each

session are computed at the start of that session,

stored in memory and then recalled whenever an en-

cryption or decryption operation for that session is

needed. It executes as follows:

• Setup Routine: is executed for every client num-

ber i (C

), once it is connected:

– A unique cryptographic random key (K

) of

length 256-bits and a random (IV

) of length

128-bits are generated and sent to the client.

– K

is expanded, using AES key setup algo-

rithm to produce the client’s encryption ex-

panded subkeys (E

) and the client’s decryption

expanded subkeys (D

). Note that both E

and

are of size 1920-bits.

– E

, D

and IV

are stored in memory.

• Encryption Execution Routine: To encrypt a

plaintext (PT) for C

– E

and IV

are fetched from memory and are

used to encrypt PT using CBC mode.

• Decryption Execution Routine: To decrypt a ci-

phertext (CT) for C

– D

and IV

are fetched from memory and is used

to decrypt CT using CBC mode.

2.3 Scheme 2

Scheme 2 is a memory dedicated scheme, where the

subkeys for encryption and decryption are computed

on-the-ﬂy, whenever an encryption or decryption op-

eration is needed. It executes as follows:

• Setup Routine: is executed for every client C

once it is connected:

– A unique cryptographic random key (K

) of

length 256-bits and a random (IV

) of length

128-bits are generated and sent to the client.

– K

and IV

are stored in memory.

– Encryption Execution Routine: To encrypt a

plaintext (PT) for C

∗ K

and IV

are fetched from memory.

∗ PT is encrypted using K

, where the encryp-

tion subkeys are computed on-the-ﬂy, and IV

using CBC mode.

– Decryption Execution Routine: To decrypt a

ciphertext (CT) for C

∗ K

and IV

are fetched from memory.

∗ CT is decrypted using K

, where the decryp-

tion subkeys are computed on-the-ﬂy, and IV

using CBC mode.

SECRYPT 2008 - International Conference on Security and Cryptography

120

3 PROPOSED SCHEME

3.1 The Requirements of Encryption

Schemes for High-Speed Networks

1-High Throughput. The faster the encryption the

better.

2-Low Memory. The less memory requirements the

better.

3-Maximum Number of Clients. The more served

clients the better.

3.2 Motivation

Scheme2 satisﬁes all these requirements except the

most important one (high throughput), on the other

hand Scheme1 can not serve a large number of con-

current clients (see Section 5). A need for a scheme

that satisﬁes all the requirements has aroused.

3.3 Proposed Scheme Objectives

1. High Throughput: It should be faster than

Scheme2 and possesses a comparable perfor-

mance as that of Scheme1.

2. Low memory: The memory requirements should

be comparable to that of Scheme 2.

3. Maximum number of clients: The maximum

number of concurrent clients should be compara-

ble to that of Scheme2.

Refer to Section 5 for more details.

3.4 AESS

AESS is a variant of AES with 256-bits key. It

is constructed using the SSM model (El-Fotouh and

Diepold, 2008). It accepts two 128-bits secondary

keys. The listing of AESS is found in table 1, where:

X: is the input plaintext, that will be encrypted using

AESS.

EK: is the expanded AES encryption key.

K1: is the ﬁrst part of the secondary key of size 128-

bits.

K2: is the second part of the secondary key of size

128-bits.

Substitute(EK,K1,i): replaces the i

128-bits of EK

with K1 (Note that: the ﬁrst round of the AES is

round zero and it is the pre-whitening process).

Table 1: AESS encrypting function.

Encrypt-AESS(X,EK,K1,K2)

Substitute(EK,K1,5)

Substitute(EK,K2,10)

C=Encrypt-AES(X,EK)

return C

Encrypt-AES(X,EK): encrypts X (using AES en-

cryption routine with 256-bits key), with EK as

the expanded encryption key and return the result.

C: the output ciphertext.

In AESS, two rounds subkey are replaced:

1. The subkeys of the ﬁfth round are replaced with

K1.

2. The subkeys of the tenth round are replaced with

K2.

3.5 SchemeS

We propose to use AESS to build a scheme for high-

speed networks, where:

• (K

) is the cluster key used as the AES secret key,

and is shared by n clients (where n is the size of a

cluster).

• Each client i (C

) has its own two unique 128-bits

keys (C

) and (C

SchemeS

tries to eliminate the key setup latency,

it executes as follows:

• Cluster Setup Routine: is used to prepare the

system and is executed once for each cluster of

n-clients.

– A cryptographic secure shared random key (K

)

with length 256-bits is generated.

– K

is expanded, using AES key setup algorithm

to produce the cluster’s shared encryption ex-

panded subkeys (E

) and the cluster’s shared

decryption expanded subkeys (D

– E

and D

are stored in the server’s memory.

• Client Setup Routine: is executed for every

client number i (C

), once it is connected:

– Three unique cryptographic 128-bits random

numbers C

, C

and IV

are generated and

sent to the client together with K

– C

, C

and IV

are stored in the server’s mem-

ory.

• Encryption Execution Routine: To encrypt a

plaintext (PT) for C

– C

, C

and IV

are fetched from the server’s

memory.

A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS

121

– PT is encrypted with AESS, where E

, C

serve as EK, K1 and K2 respectively deﬁned in

table 1 and IV

is used as the initial vector for

the CBC mode.

• Decryption Execution Routine: To decrypt a ci-

phertext (CT) for C

– C

, C

and IV

are fetched from the server’s

memory.

– CT is decrypted with the decryption routine of

AESS using D

, C

as EK, K1 and K2

respectively deﬁned in table 1 and IV

is used

as the initial vector for the CBC mode.

4 MEMORY ANALYSIS

The less the memory the scheme needs, the more

available memory to other applications and the larger

the number of concurrent clients the server can serve.

Memory access has a great role in the overall scheme

performance. If a server has insufﬁcient physical

memory space to cache all of the data necessary for

the execution of its local threads, it has to perform

page replacements for data not located on physical

memory. Although the technology of virtual memory

makes the server able to complete the work of its lo-

cal threads, the latency of memory accesses caused by

page replacements postpones the execution of those

threads. This factor currently becomes more impor-

tant to program performance since the cost of disk ac-

cesses is very expensive compared to the cost of data

computation (Liang et al., 2003).

Table 2 presents the memory requirements in bits

of each scheme per client to hold the key material.

For scheme1:

• The AES Equivalent Inverse Cipher uses different

subkeys for decryption than those for encryption,

except for the ﬁrst and last round. That is why we

need to store only 3584-bits instead of 3840-bits.

For scheme2:

• 256-bits are needed for encryption/decryption to

hold the intermediate round subkeys, as not to

overwrite the key itself.

• In case both encryption and decryption are

needed, 512-bits are required to hold the interme-

diate values of encryption and decryption round

keys, to allow simultaneous encryption and de-

cryption operations to take place.

For SchemeS

• 256-bits are needed for encryption/decryption to

hold C

and C

for the client C

Table 2: Memory required in bits by each scheme for every

client.

Encryption Decryption Both

Scheme1 1920 1920 3584

Scheme2 512 512 768

SchemeS

(1920/n)+256 (1920/n)+256 (3584/n)+256

• In case of encryption: an expanded key is required

for each n clients.

• In case of decryption: an expanded key is required

for each n clients.

• As n increases the overhead of storing the cluster

expanded key decreases.

5 SIMULATION ANALYSIS

In order to gain more insight on the practical behavior

of the schemes, we designed a simulation program to

explore the schemes properties. We ran the simulation

with different parameters to investigate their inﬂuence

on each scheme. This simulation analysis is intended

to demonstrate the performance and behavior of the

schemes. We have developed four scenarios that can

model various classes of network applications, these

scenarios are:

Scenario 1: models network applications that do not

use disk operations (e.g. a chat server, where the

encrypted packets are transmitted from client to

another).

Scenario 2: models network applications that read

form the disk (e.g. a query server, where the client

sends a query and receives the results).

Scenario 3: models network applications that write

to the disk (e.g. a database server, where the data

sent by the client is stored in the database).

Scenario 4: models network applications that read

from and write to the disk (e.g. a query server that

logs the queries of the clients, where the client

sends a query and receives the results and the

client’s query is stored in the database).

5.1 Server Conﬁguration

We implemented NoCrypto, Scheme1, Scheme2 and

SchemeS* using C++ language and run a simulation

to examine their practical behavior. Table 3 shows

the server conﬁguration. Note that NoCrypto does not

perform any encryption or decryption functions, it is

illustrated here to show the cryptographic overhead

and in SchemeS* all the clients share the same cluster.

SECRYPT 2008 - International Conference on Security and Cryptography

122

Table 3: Server conﬁguration.

Processor PIV 3 GHz

RAM 2048 MB

Processor Cache 2 MB

Paging ﬁle 2048 MB

OS Microsoft Windows XP

Data pool 1 GB

Compiler Visual C++ 2005

Code optimization Maximum speed

5.2 Parameters

• α is the tested packet size, we chosen α to be ei-

ther 40 or 1500 bytes. As the current packet sizes

seem mostly bimodal at 40 and 1500 bytes (Greg,

1998; Sinha et al., 2007).

• P is the number of packets sent by each client, we

chose P equals to 10 in case α=1500 and P equals

to 100 in case α=40. This is to reduce the cost of

client setup and gives us a better understanding on

how each scheme works.

• Z

is the current number of clients served by the

server.

– We measured N, the maximum number of

clients that the server can serve for Scheme1

(as Scheme1 can serve the minimum number

of clients).

– We construct the set Z = { Z

}, where 0 ≤ i ≤

9 and Z

= (N ÷ 10) × (1 + i), here we divide

N to ten equal intervals.

• F is a ﬁle of size 1 GB used to demonstrate the

effect of disk operations.

5.3 The Scenarios

We constructed a multi-client/server TCP socket ap-

plication to demonstrate the behavior of the schemes.

The server and the clients are connected via a LAN

(100 Mbps). The scenarios work as follows:

1. The server allocates 1 GB as a shared data pool.

This pool hold the encrypted and decrypted data

for all the client and is used to illustrate the effect

of reading and writing to the RAM.

2. The server allocates the memory needed by the

tested scheme to serve Z

clients, where for each

client, the server allocates ( M+ β) bytes, where M

is the number of bytes required by each client us-

ing the tested scheme to allocate the key material

and β equals to 20 bytes (4 bytes as clients iden-

tiﬁcation number and 16 bytes to hold the client’s

IV).

3. The server waits until 10 computers are con-

nected, then send the start command to all

the computers (each computer simulates Z

/10

clients). Note that each computer is served using

a different thread, to illustrate the effect of multi-

threading.

4. As the computer receives the start command, it

sends P packets to the server, each of size α.

5. In senario 1, when the server receives a packet:

(a) The packet is decrypted for client C

and en-

crypted to client C

, where i and x are positive

random numbers less than Z

(b) The server sends the encrypted packet (from

the previous step), to the computer that serves

client C

6. In senario 2, when the server receives a packet:

(a) The packets is decrypted for client C

, where i

is a positive random number less than Z

(b) A random record of size α is read from the ﬁle

F. This record is encrypted for the client C

This is to illustrate the disk read operation.

the previous step), to the computer that sends

the packet.

7. In senario 3, when the server receives a packet:

(a) The packets is decrypted for client C

, , where

i is a positive random number less than Z

(b) The decrypted packet is encrypted and saved

at a random location to a ﬁle F. This is to il-

lustrate the disk write operation.

8. In senario 4, when the server receives a packet:

(a) The packets is decrypted for client C

, where i

is a positive random number less than Z

(b) The decrypted packet is saved at a random lo-

cation to a ﬁle F. This is to illustrate the disk

write operation.

ﬁle F, this record is encrypted for the client C

This is to illustrate the disk read operation.

(d) The server send the encrypted packet (from

the previous step), to the computer that sends

the packet.

9. When all the P packets are processed by the server

and received by the computer, the computer starts

to send P packets for the next client it simulates.

A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS

123

10. The average time τ (in milliseconds) for process-

ing a packet of size α for Z

clients is reported

(from the time the server starts to receive the in-

coming packet, till the time the server sends the

outgoing packet).

11. Note that for all the scenarios, we assume that the

incoming and outgoing packets are of the same

size for simplicity.

5.4 The Simulation Results

• We constructed and measured a set σ = { σ

where 0 ≤ i ≤ 9, where σ

is the average time

to process P packets using the examined scheme,

when it process Z

clients, using different values

of α.

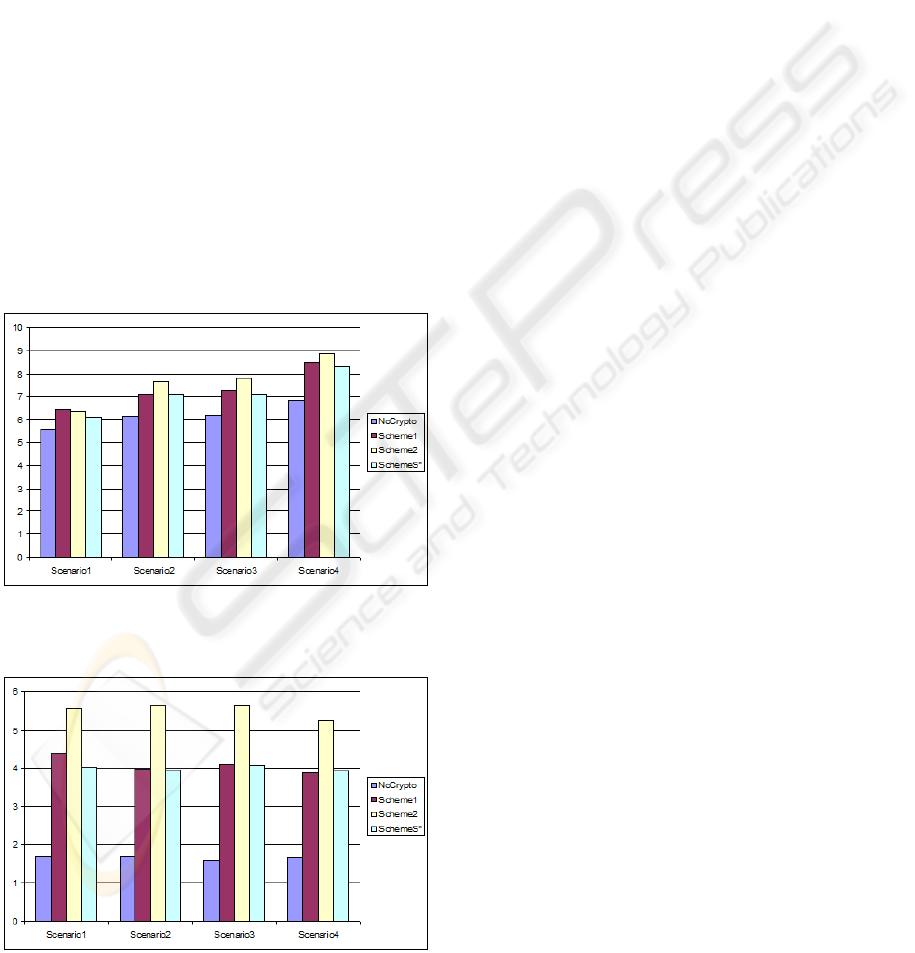
• Figure 1 and Figure 2 summarize the results of

the simulation for the four scenarios, where we

plotted the average value of σ for each scheme.

• Note that values in Figure 1 and Figure 2 are mea-

sured in milliseconds.

Figure 1: Average time needed to process 100 packets of

size 40 bytes.

Figure 2: Average time needed to process 10 packets of size

1500 bytes.

5.5 Discussion of the Results

5.5.1 Case α=40

Scenario 1: The encryption overhead ranges from

about 9% to 15%. SchemeS* is faster than

Scheme1 with about 5%, as Scheme1 is more

prone to cache misses and page faults (beacuse it

uses more memory to hold the pre-computed ex-

panded subkeys). Scheme2 possesses almost the

same speed as Scheme1.

Scenario 2: The encryption overhead ranges from

about 14% to 24%. SchemeS* possess almost the

same speed as Scheme1 and they are faster than

Scheme2 with about 8%.

Scenario 3: The encryption overhead ranges from

about 14% to 26%. SchemeS* is faster than

Scheme1 with about 2% and Scheme2 is the slow-

est scheme.

Scenario 4: The encryption overhead ranges from

about 21% to 29%. SchemeS* is faster than

Scheme1 with about 2% and Scheme2 is the slow-

est scheme.

In conclusion, in case of small packets (α= 40, which

represents about 40% of the internet trafﬁc (Sinha

et al., 2007)), SchemeS* is faster than Scheme1 and

Scheme2.

5.5.2 Case α=1500

Scenario 1: The encryption overhead ranges from

about 141% to 231%. SchemeS* is faster than

Scheme1 with about 8%, as Scheme1 is more

prone to cache misses and page faults (beacuse it

uses more memory to hold the pre-computed ex-

panded subkeys). Scheme2 is about 37% slower

than SchemeS*.

Scenario 2: The encryption overhead ranges from

about 136% to 235%. SchemeS* and Scheme1

possess almost the same speed, on the other hand

Scheme2 is about 42% slower than them.

Scenario 3: The encryption overhead ranges from

about 155% to 253%. SchemeS* and Scheme1

possess almost the same speed, on the other hand

Scheme2 is about 38% slower than them.

Scenario 4: The encryption overhead ranges from

about 124% to 216%. SchemeS* and Scheme1

possess almost the same speed, on the other hand

Scheme2 is about 33% slower than them.

In conclusion, in case of large packets (α= 1500,

which represents about 20% of the internet traf-

ﬁc (Sinha et al., 2007)), SchemeS* and Scheme1 out-

SECRYPT 2008 - International Conference on Security and Cryptography

124

performs Scheme2. Note that the overhead of fetch-

ing the pre-computed expanded subkeys of Scheme1

is considered neglegted in case of large packets.

5.5.3 The Maximum Number of Clients

SchemeS* uses the least amount of memory to hold

its key material, thus can serve the maximum num-

ber of concurrent clients (by using the same mem-

ory, SchemeS* can serve up to 14 times the maxi-

mum number of clients served by Scheme1 and up

to 3 times the maximum number of clients served by

Scheme2).

6 SECURITY ANALYSIS

6.1 Assumptions

1. The secondary key is a part of the secret key and

not controlled by the attacker.

2. AES’ key scheduling routine, produces a random

expanded key.

3. AES is secure, when a random expanded key is

used.

(a) Due to our second assumption, AES is secure.

(b) Note that all the non-linearity of the AES is of-

fered by its ﬁxed S-box (Daemen and Rijmen,

1998), not from the key material.

6.2 Security of CBC

Birthday attacks on CBC mode remain possible even

when the underlying block cipher is ideal (Bellare

et al., 1997), and CBC encryption becomes inse-

cure once 2

(in case of AES) blocks have been en-

crypted, in the sense that at this point partial informa-

tion about the message begins to leak, due to birthday

attacks (Bellare et al., 1998). Therefore, the server

MUST generate a fresh key (random and unused key)

before 2

blocks are encrypted with the same key for

each client. We recommend to encrypt maximum 2

blocks for each client (which is sufﬁcient to encrypt

the largest possible IPv6 jumbogram (Borman et al.,

1999)), then generates a fresh key for that client, to

avoid birthday attacks.

6.3 Security of AES

We assume that, the best attack known against AES

is to try every possible 256-bits key (i.e., perform an

exhaustive key search), this requires about 2

255

trails

(when AES with 256-bits is used).

6.4 Security of AESS

For an attacker that does not know either the primary

key and the secondary key, and she tries to attack a

normal AES with some random independent subkeys,

which is secure due to our third assumption.

Notes:

1. The secondary key replaces the subkeys of ﬁfth

and tenth rounds of the AES (with 256-bits en-

cryption key), to achieve full confusion and full

diffusion in both the encryption and decryption

directions, as AES requires only four rounds to

achieve full bit confusion (or mixing) and dif-

fusion (each input bit affecting each output bit)

properties (May et al., 2002).

2. This choice assures that any difference between

two secondary keys, will be associated with full

confusion and full diffusion in both the encryption

and decryption directions.

6.5 Security of the Schemes

The security of Scheme1 and Scheme2 are inherited

from the security of the CBC mode and that of the

AES. As the attacker can either attack the mode of op-

eration or the cipher itself. The security of SchemeS

is inherited from that of the CBC mode and that of

AESS. As CBC mode security is not based on the

used block cipher. There are two kinds of attackers

on SchemeS, when attacking AESS:

1. An attacker A that watches the ciphertext. For

an external attacker (that does not possess the pri-

mary key), it is hard to gain advantage, when the

secondary keys do not share a common mathemat-

ical relation, to mount a related key attack.

2. An attacker B (which is a client of the server), that

would like to attack another client within the same

cluster. This attacker knows the primary key:

(a) The attacker encrypts the known plaintext

with the known primary key until the 5

round (without the AddRoundKey operation)

to produce the intermediate state φ.

(b) The attacker decrypts the known ciphertext

with the known primary key until 10

round

to produce the intermediate state γ.

duce AESS to an Even-Mansour construc-

tion (Even and Mansour, 1997), where K1

and K2 are the keys and the reduced AES (5

rounds) is considered as the (Pseudo)random

permutation. Note that it was evident that

A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS

125

the AES has a random proﬁle after only 3

rounds (Soto and Bassham, 2000).

(d) The security of Even-Mansour is:

i. About 2

255

, using exhaustive search over

the key space (K1 and K2 are both of size

128-bits), which is considered large enough

by todays standards.

ii. Daemen demonstrated in (Daemen, 1991)

that a known plaintext attack, will take on

average 2

127

calculations, which has the

same complexity as attacking AES with

128-bits key, which is considered secure

with todays technology.

iii. Daemen also demonstrated in (Daemen,

1991) that a chosen plaintext attack, will

take on average 2

calculations using 2

stored blocks. By limiting the number of

encrypted blocks per client, this attack can

be avoided (see Section 6.2, as each client

encrypts maximum 2

blocks using the

same secondary key, if for some applica-

tion more data is needed to be encrypted the

client can join a new cluster ”using a fresh

secondary key” or new fresh secondary key

can be generated for that client).

iv. Biryukov-Wagner demonstrated in

(Biryukov and Wagner, 2000), that a

”sliding with a twist” attack allows an ad-

versary to recover the key using

√

2 ×2

known plaintexts and

√

2 ×2

work. By

limiting the number of blocks encrypted

per client using the same secondary key,

this attack can be avoided (see Section 6.2).

The most powerful attacker is B, where an inside at-

tacker attack a client in the same cluster. This happens

with probability (n-1)/(N-1). So as n decreases and/or

N increases, the probability of the existence of such

attacker decreases. Even if attacker B exists, the com-

plexity to mount Daemen’s known plaintext attack is

the same complexity to attack AES with 128-bits key,

which is considered secure with todays technology.

On the other hand, to limit the probability of the other

attacks, the number of encrypted blocks per client (us-

ing the same secondary key) MUST NOT reach the

boundary. Therefore the server MUST generate a

fresh key (for each client) before 2

blocks are en-

crypted with the same key. We recommend that the

server encrypts maximum 2

blocks for each client,

if for some application more data is needed to be en-

crypted the client can join a new cluster or new fresh

secondary key can be generated for that client.

So SchemeS

is upper bounded with the secu-

rity of AESS and lower bounded with the security of

Even-Mansour.

7 CONCLUSIONS

In this paper, we proposed a novel encryption scheme

for high-speed networks. We analyzed our proposed

scheme with the two most widely used schemes. Our

analysis consists of theoretical and practical parts.

This analysis illustrates that our proposed scheme is

superior than the current schemes, by possessing high

throughput, consuming the lowest amount of mem-

ory, serving the largest number of concurrent clients

and it is also considered secure.

REFERENCES

Bellare, M., Desai, A., Jokipii, E., and Rogaway, P. (1997).

A Concrete Security Treatment of Symmetric Encryp-

tion. In FOCS ’97: Proceedings of the 38th An-

nual Symposium on Foundations of Computer Science

(FOCS ’97), page 394, Washington, DC, USA. IEEE

Computer Society.

Bellare, M., Krovetz, T., and Rogaway, P. (1998). Luby-

Rackoff backwards: Increasing security by making

block ciphers non-invertible. Lecture Notes in Com-

puter Science, 1403.

Biryukov, A. and Wagner, D. (2000). Advanced Slide At-

tacks. In Advances in Cryptology—Eurocrypt ’00 Pro-

ceeding.

Borman, D., Deering, S., and Hinden, R. (1999). IPv6 Jum-

bograms. RFC 2675.

Daemen, J. (1991). Limitations of the Even-Mansour Con-

struction. In ASIACRYPT: Advances in Cryptology

– ASIACRYPT: International Conference on the The-

ory and Application of Cryptology. LNCS, Springer-

Verlag.

Daemen, J. and Rijmen, V. (1998). AES Proposal: Rijndael.

http://citeseer.ist.psu.edu/daemen98aes.html.

Dunn, J. and Martin, C. (2000). Terminology for ATM

Benchmarking. RFC 2761.

El-Fotouh, M. and Diepold, K. (2008). Dynamic Substi-

tution Model. In The Fourth International Confer-

ence on Information Assurance and Security (IAS’08),

Naples, Italy.

Even, S. and Mansour, Y. (1997). A Construction of a Ci-

pher from a Single Pseudorandom Permutation. Jour-

nal of Cryptology: the journal of the International As-

sociation for Cryptologic Research, 10(3):151–161.

Gaj, K. and Chodowiec, P. (1999). Hardware performance

of the AES ﬁnalists - survey and analysis of results.

http://ece.gmu.edu/crypto/AES survey.pdf.

Gladman, B. (2006). AES optimized C/C++ code. http: //

fp.gladman.plus.com/ AES /index.htm.

Greg, C. (1998). The nature of the beast: Recent Traf-

ﬁc Measurements from an Internet backbone. cite-

seer.ist.psu.edu/673025.html.

SECRYPT 2008 - International Conference on Security and Cryptography

126

Jung, O., Kuhn, S., Ruland, C., and Wollenweber, K.

(2001). Enhanced Modes of Operation for the En-

cryption in High-Speed Networks and Their Impact

on QoS. In ACISP ’01: Proceedings of the 6th Aus-

tralasian Conference on Information Security and Pri-

vacy, pages 344–359, London, UK. Springer-Verlag.

Kent, S. and Atkinson, R. (1998a). IP Authentication

Header. RFC 2402.

Kent, S. and Atkinson, R. (1998b). IP Encapsulating Secu-

rity Payload (ESP). RFC 2406.

Kent, S. and Atkinson, R. (1998c). Security Architecture

for the Internet Protocol. RFC 2401.

Lai, Y., Chang, L., Chen, L., Chou, C., and Chiu, C. (2004).

A novel memoryless AES cipher architecture for net-

working applications. In ISCAS (4), pages 333–336.

Li, H. and Li, J. (2005). A High Performance Sub-Pipelined

Architecture for AES. In ICCD ’05: Proceedings of

the 2005 International Conference on Computer De-

sign, Washington, DC, USA. IEEE Computer Society.

Liang, T., Liu, Y., and Shieh, C. (2003). Adding Mem-

ory Resource Consideration into Workload Distribu-

tion for Software DSM Systems. In CLUSTER, pages

362–369.

May, L., Henricksen, M., Millan, W., Carter, G., and Daw-

son, E. (2002). Strengthening the Key Schedule of

the AES. In ACISP ’02: Proceedings of the 7th Aus-

tralian Conference on Information Security and Pri-

vacy, pages 226–240, London, UK. Springer-Verlag.

Menezes, A., Oorschot., P. V., and Vanstone, S. (1996).

Handbook of Applied Cryptography. CRC Press.

NIST (2001). Announcing the ADVANCED ENCRYP-

TION STANDARD (AES). Technical Report 197,

Federal Information Processing Standards Publica-

tion.

Schneier, B., Kelsey, J., Whiting, D., Wagner, D., Hall, C.,

and Ferguson, N. Performance Comparison of the

AES Submissions.

Sinha, R., Papadopoulos, C., and Heidemann, J. (2007). In-

ternet Packet Size Distributions: Some Observations.

Technical Report ISI-TR-2007-643, USC/Information

Sciences Institute. Orignally released October 2005 as

web page http://netweb.usc.edu/

rsinha/pkt-sizes/.

Sklavos, N., Moldovyan, N. A., and Koufopavlou, O.

(2005). High speed networking security: design and

implementation of two new DDP-based ciphers. Mob.

Netw. Appl., 10(1-2):219–231.

Soto, J. and Bassham, L. (2000). Randomness Testing

of the Advanced Encryption Standard Finalist Candi-

dates. Computer Security Division,National Institute

of Standards and Technology.

Stats, I. W. (2008). WORLD INTERNET US-

AGE AND POPULATION STATISTICS.

http://www.internetworldstats.com/stats.htm.

Tan, Z., Lin, C., Yin, H., and Li, B. (2004). Optimization

and Benchmark of Cryptographic Algorithms on Net-

work Processors. IEEE Micro, 24(5):55–69.

Tillich, S. and Groschdl, J. (2006). Instruction Set Exten-

sions for Efﬁcient AES Implementation on 32-bit Pro-

cessors. In Cryptographic Hardware and Embedded

Systems CHES 2006, volume 4249 of Lecture Notes

in Computer Science, pages 270–284. Springer Ver-

lag.

Walker, J. (2000). 802.11 Security Series, Part III: AES-

based Encapsulations of 802.11 Data. http://cache-

www.intel.com/cd/00/00/01/77/17770 80211 part3.pdf.

A FAST ENCRYPTION SCHEME FOR NETWORKS APPLICATIONS

127