A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL

INCONSISTENCY DIAGNOSIS IN FIREWALL RULE SETS

S. Pozo, R. Ceballos and R. M. Gasca

Department of Computer Languages and Systems, ETS Ingeniería Informática, University of Seville

Avda. Reina Mercedes S/N, 41012 Sevilla, Spain

Keywords: Diagnosis, consistency, conflict, anomaly, firewall, acl, ruleset.

Abstract: Firewall ACLs can contain inconsistencies. There is an inconsistency if different actions can be taken on the

same flow of traffic, depending on the ordering of the rules. Inconsistent rules should be notified to the

system administrator in order to remove them. Minimal diagnosis and characterization of inconsistencies is

a combinatorial problem. Although many algorithms have been proposed to solve this problem, all reviewed

ones work with the full ACL with no approximate heuristics, giving minimal and complete results, but

making the problem intractable for large, real-life ACLs. In this paper we take a different approach. First,

we deeply analyze the inconsistency diagnosis in firewall ACLs problem, and propose to split the process in

several parts that can be solved sequentially: inconsistency detection, inconsistent rules identification, and

inconsistency characterization. We present polynomial heuristic algorithms for the first two parts of the

problem: detection and identification (diagnosis) of inconsistent rules. The algorithms return several

independent clusters of inconsistent rules that can be characterized against a fault taxonomy. These clusters

contains all inconsistent rules of the ACL (algorithms are complete), but the algorithms not necessarily give

the minimum number of clusters. The main advantage of the proposed heuristic diagnosis process is that

optimal characterization can be now applied to several smaller problems (the result of the diagnosis process)

rather than to the whole ACL, resulting in an effective computational complexity reduction at the cost of not

having the minimal diagnosis. Experimental results with real ACLs are given.

1 INTRODUCTION

A firewall is a network element that controls the

traversal of packets across different network

segments. It is a mechanism to enforce an Access

Control Policy, represented as an Access Control

List (ACL). An ACL is in general a list of linearly

ordered (total order) condition/action rules. The

condition part of the rule is a set of condition

attributes or selectors, where |condition|=k (k is the

number of selectors). The condition set is typically

composed of five elements, which correspond to five

fields of a packet header (Taylor, 2005). In firewalls,

the process of matching TCP/IP packets against

rules is called filtering. A rule matches a packet

when the values of each field of the header of a

packet are subsets or equal to the values of its

corresponding rule selector. The action part of the

rule represents the action that should be taken for a

matching packet. In firewalls, two actions are

possible: allow or deny a packet. A firewall ACL is

commonly denominated a rule set.

Firewalls have to face many problems in real-life

modern networks (Wool, 2004). One of the most

important ones is rule set consistency. Selectors of

rules can overlap (for example, the protocol

selector), and can even be rules that are totally equal

to others. Since a packet can be matched with any of

the overlapping rules, firewalls usually use a

positional conflict resolution technique, taking the

action of the first matching rule. An inconsistent

firewall ACL implies in general a design error, and

indicates that the firewall is accepting traffic that

should be denied or vice versa.

The minimal inconsistency characterization is a

combinatorial problem. Although many algorithms

have been proposed to solve it, to the best of our

knowledge, all of them are brute force. These results

return an optimal characterization, but make the

problem intractable for large real-life rule sets.

In this paper we propose to take a different

approach in order to make the problem tractable for

real-life, big rule sets. We propose to divide

consistency management in three sequential stages:

430

Pozo S., Ceballos R. and M. Gasca R. (2008).

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE SETS.

In Proceedings of the International Conference on Security and Cryptography, pages 430-441

DOI: 10.5220/0001921504300441

 SciTePress

• Inconsistency detection. It is the action of

finding the rules that are inconsistent with other

rules

• Identification of inconsistent rules. Finding the

rules that cause the inconsistencies among the

detected inconsistent rules, and whose removal

produces a consistent rule set.

• Inconsistency characterization is understood as

the action of naming the identified inconsistent

rules among an established taxonomy of faults.

This paper focuses in the first two parts of the

process (detection and identification, diagnosis). As

we will show, detection is a problem that can be

solved in polynomial time with complete algorithms.

However, optimal identification and characterization

are combinatorial problems. In this paper, we

propose best case O(n) and worst case O(n

) time

complexity order independent detection and

identification algorithms with the number of rules of

the rule set, n. Algorithms are capable of handling

full ranges in rule selectors without doing rule

decorrelation, range to prefix conversion, or any

other pre-process. A Java tool is available.

We consider this work a significant advance in

consistency diagnosis in firewall rule sets because

isolating diagnosis from characterization can reduce

the effective computational complexity of optimal

characterization algorithms, since they can now

applied to several smaller problems (the result of the

diagnosis stage) rather than to a big one (the full rule

set). The work presented in this paper is an

improvement over a previous presented one (Pozo,

2008). In this paper, best case has been improved by

and order of magnitude and worst case by a

constant. Although the worst case improvement may

not seem representative in theoretical results, we

will show that this improvement is very important in

real-life rule sets, since they are near the best case.

This paper is structured as follows. In section 2,

we analyze the internals of the consistency

management problem in firewall rule sets. In section

3 we propose the consistency-based diagnosis

algorithms, give a theoretical complexity analysis

and experimental results with real rule sets. In

section 4 we review related works comparing them

to our proposal. Finally we give some concluding

remarks in section 5.

2 ANALYSIS OF THE

CONSISTENCY PROBLEM

To understand the problem, it is important to firstly

review the inconsistencies characterized in the

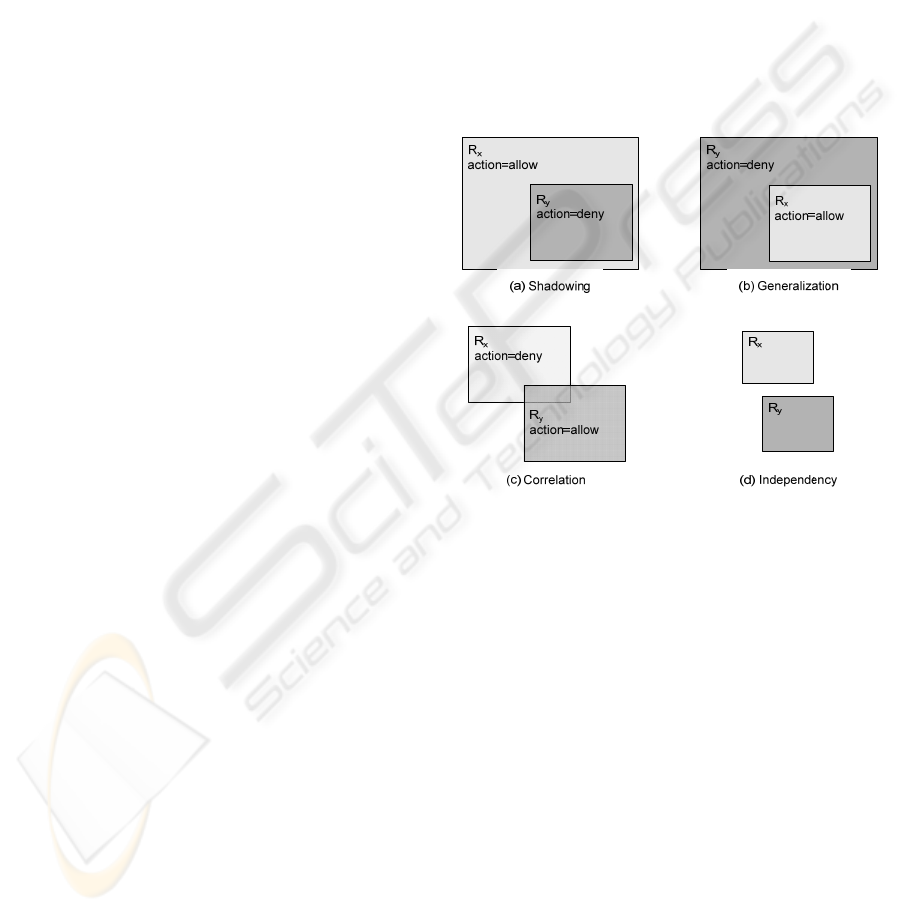
bibliography. A complete characterization that

includes shadowing, generalization, correlation and

redundancy has been given in (Al-Shaer, 2006).

Although all of these are inconsistencies, usually not

all are considered to be errors, as it can be used to

cause desirable effects. All of these inconsistencies

except redundancy are graphically represented in

Fig. 1. For the sake of simplicity, only two rule

inconsistencies with one selector are represented. An

example of an ACL is presented in Table 1.

Figure 1: Graphical representation of three

inconsistencies.

In this paper, we propose to divide consistency

management in three sequential stages (Fig. 2). In

the first step, all inconsistent rules are detected.

Then, the minimal number of rules that cause the

detected inconsistencies should be identified. Their

removal guarantees that the resulting rule set is

consistent. These two stages are called Inconsistency

Diagnosis. Finally, the identified inconsistent rules

are characterized among a established taxonomy of

firewall rule set inconsistencies. The detection part

of the process can be solved with complete

polynomial algorithms (the most important are

reviewed in the related works section, and a new one

is proposed in this paper). The minimal

identification is a combinatorial problem, as is going

to be showed in the next section. A polynomial

heuristic algorithm is proposed in this paper. The

third and last problem is also combinatorial (Pozo4,

2008) (the most important works are reviewed later

in this paper). Diagnosis is also rule-order

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

431

Table 1: Example of a Firewall Rule Set.

Priority/ID Protocol Source IP Src Port Destination IP Dst Port Action

R1 tcp 192.168.1.5 any *.*.*.* 80 deny

R2 tcp 192.168.1.* any *.*.*.* 80 allow

R3 tcp *.*.*.* any 172.0.1.10 80 allow

R4 tcp 192.168.1.* any 172.0.1.10 80 deny

R5 tcp 192.168.1.60 any *.*.*.* 21 deny

R6 tcp 192.168.1.* any *.*.*.* 21 allow

R7 tcp 192.168.1.* any 172.0.1.10 21 allow

R8 tcp *.*.*.* any *.*.*.* any deny

R9 udp 192.168.1.* any 172.0.1.10 53 allow

R10 udp *.*.*.* any 172.0.1.10 53 allow

R11 udp 192.168.2.* any 172.0.2.* any allow

R12 udp *.*.*.* any *.*.*.* any deny

independent, contrarily to characterization. The main

difference of this work with other ones is that other

authors apply brute force algorithms to solve directly

the characterization problem, with no previous

diagnosis. This yields algorithms that cannot be

applied to big rule sets. With the proposed approach,

the same characterization algorithms can be applied

to several smaller problems, rather than to the full

rule set. However, the number of these smaller

problems is not minimal with the given heuristic

algorithms proposed in this paper. In addition,

heuristic characterization algorithms (Pozo4, 2008)

can also be used to make the problem fully tractable.

Figure 2: Consistency management process.

2.1 One to One Consistency in Firewall

Rule Sets

First, it is needed to formalize a firewall rule set.

• Let RS be a firewall rule set consisting of n

rules,

{

}

,...

RS R R= .

• Let

,,R H Action H=< > ∈  be a rule, where

{

}

ction allow deny= is its action.

• Let

[],1 ,

Rk k nk

≤

≤∈

•

{

}

,_,_,_,_protocol src ip src prt dst ip dst prt

be a selector of a firewall rule R

• Let ‘<’ and ‘>’ be operators defined over the

priority of the rules, where R

< R

implies that

then R

has more priority than R

and its action

is going to be taken first, and vice versa.

Attending to Al-Shaer characterization, two rules

, R

) are correlated if they have a relation

between all of its selectors, and have different

actions. Fig. 1(c) represents a correlation

inconsistency between two rules with one selector

each. As the figure shows, the relation between the

rules is not subset, nor superset, nor equal (rules R1

and R3 of Table 1 are correlated). Fig. 1(a)

represents a shadowing inconsistency between two

rules. The relation is equality or subset of the

shadowed rule, R

, respect to the general rule, R

with R

(R4 is shadowed by R3 in Table 1

example). Fig. 1(b) represents a generalization

inconsistency between two rules, which is the

inverse of shadowing respect to the priority of the

rules. The relation is superset of the general rule

respect to the other one (R2 is a generalization of R3

in Table 1 example).

Since we are only interested in diagnosis and not

in characterization, let’s try to remove names and

give a general case of inconsistency based on these

inconsistency characterizations (except redundancy).

In a closer look at shadowing and generalization

inconsistencies in Fig. 1, it can be seen that, in

reality, these two inconsistencies are the same one,

and the only thing that differentiates them is the

priority of the rules. Thus, if priority is ignored,

these two inconsistencies are special cases of a

SECRYPT 2008 - International Conference on Security and Cryptography

432

correlation. That is, shadowing can be redefined as a

correlation where all selectors of one rule (the

shadowed one) are subsets or equal of the general

rule. As generalization is the inverse with respect to

the priority of shadowing, a generalization

inconsistency can also be redefined as a correlation

where of all selectors of a rule (the general one) are

supersets of the other rule. So, the correlation

inconsistency can be redefined as the superset of all

inconsistencies, representing the most general case.

For that reasons, it is possible to define rule

inconsistency in only one priority independent case

that recognizes all characterized inconsistencies.

This is a key issue for our diagnosis process.

Definition 2.1. Inconsistency. Two rules

RR RS∈ are inconsistent if and only if the

intersection of each of all of its selectors R[k] is not

empty, and they have different actions,

independently of their priorities. The inconsistency

between two rules expresses the possibility of an

undesirable effect in the semantics of the rule set.

The semantics of the rule set changes if an

inconsistent rule is removed.

{}

(, )1 1 ,

[][] [][]

,_,_,_,_

ij i j

nconsistent R RS i n R RS j n j i

R k R k R Action R Action

k protocol src ip src prt dst ip dst prt

≤≤ ⇔∃ ∈ ≤ ≤ ≠•

≠∅∧ ≠

∀∈

∩

Inconsistency of one rule in a RS

{}

(, , )1 , ,

[] [] [ ] [ ]

,_,_,_,_

ij i j

Inconsistent R R RS i j n i j

R k R k R Action R Action

k protocol src ip src prt dst ip dst prt

≤≤≠⇔

≠∅∧ ≠

∀∈

∩

Inconsistency between two rules in a RS

This definition can be extended to more than two

rules, as is going to be explained in the next section.

Attending to Definition 2.1, all cases represented in

Fig. 1 are of the same kind, and are called

inconsistencies without any particular

characterization. Priority is only required if

inconsistencies are going to be characterized. We

showed that all inconsistencies between pairs of

rules can be detected by pairs of two with Definition

2.1, but more complicated situations must also be

analyzed in order to illustrate this definition. In next

sections we show that no extension is needed to

Definition 2.1, since the case of n to one rule

inconsistency can be decomposed in several

independent two-rule inconsistencies.

2.2 One to Many Consistency in

Firewall Rule Sets

All base situations are presented in Fig. 3, which is

an extension to Fig. 1. This figure is a simplification

to three inconsistent rules, but can easily be

extended to more rules that can be composed in

several ways.

Fig. 3(a1) represents an inconsistency where the

union of two independent rules R

, R

overlaps with

another one, R

(Fig. 4(a) taken from (García-Alfaro,

2007) exemplifies this situation). As R

inconsistent with R

, and R

is also inconsistent with

, both in an independent manner, this situation can

be decomposed in two independent inconsistencies,

and can easily be diagnosed.

Action=deny

Action=allow

Action=deny

(a1)

Action=allow

Action=deny

(b1)

allow

(a2) (b2)

Action=deny

allow

Action=deny

(c)

Action=deny

Action=allow

Figure 3: Graphical representation of inconsistencias

between three rules.

Fig. 3(a2) presents a similar situation, where R

overlaps with the union of R

and R

. This situation

is also decomposable in two independent

inconsistencies: R

inconsistent with R

, and R

with

. Note that, in order to diagnose inconsistencies,

the priority of the rules is not necessary.

The situations presented in Fig. 3(b1) and Fig.

3(b2) are the inverse of the two previous ones

respect to the action. Thus, the diagnosis is

analogous. This situation is exemplified in Fig. 4(b).

Finally, Fig. 3(c) represents a relation with three

overlapping rules (an example is in Fig. 4(c)). This

situation can also be decomposed in two

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

433

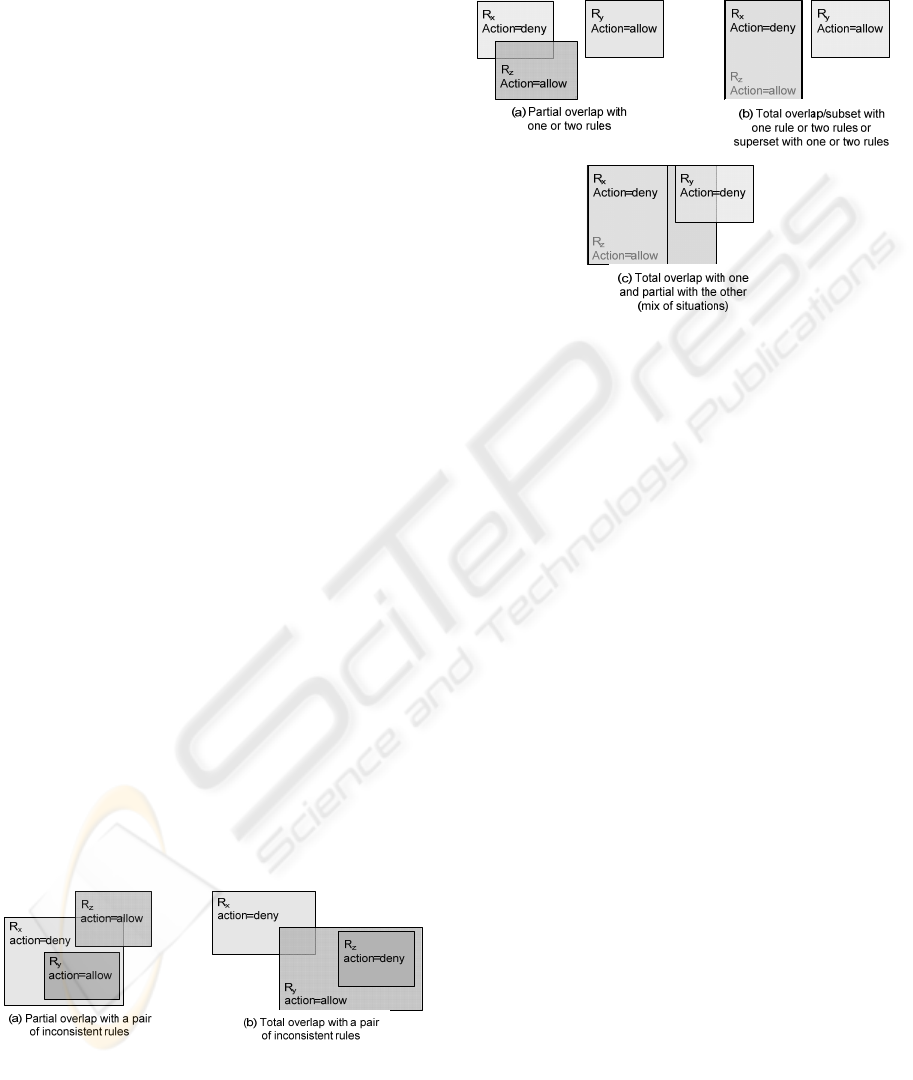
independent ones: R

inconsistent with R

, and R

with R

In conclusion, it is possible to diagnose

inconsistencies between an arbitrary number of rules

with Definition 2.1, because all the presented

situations can be decomposed in independent two by

two relations. These examples are easily extendable

to more than three rules.

{

}

{

}

{}{}

: [10 50]

:[4090]

:[3080]

x port allow

y port allow

z port deny

∈− ⇒

(a)

{

}

{

}

{}{}

: [10 50]

: [40 90]

:[0100]

y port allow

z port allow

x port deny

∈− ⇒

(b)

{

}

{

}

{}{}

:[050]

: [60 100]

:[4070]

Rx port deny

z port deny

y port allow

∈− ⇒

(c)

Figure 4: Inconsistency examples.

If a new rule, R

, is added to an inconsistent rule

set, the new rule can only cause a new inconsistency

with one to all of the rules in the rule set, in a similar

way that it did in the previous case (Fig. 5). It cannot

modify a previous inconsistency, or cause an

inconsistency between two consistent rules, and

without the new rule. This inconsistency can also be

decomposed in two by two inconsistencies, which

are independent of the inconsistencies that were

present in the rule set previously to the addition of

. In the same way, if a new rule is inserted in a

consistent rule set, a similar decomposition can be

done (Fig. 6).

Figure 5: Graphical representation of a new inconsistent

rule added in an inconsistent rule set.

Note that, as the diagnosis process is order-

independent, the new rule can be inserted anywhere

in the rule set. Again, these two situations can be

easily extended to more than three rules.



Figure 6: Graphical representation of a new inconsistent

rule added in an consistent rule set.

3 CONSISTENCY-BASED

DIAGNOSIS OF RULE SETS

The presented analysis has motivated the separation

of characterization from diagnosis, and to solve the

diagnosis problem in isolation, as a first stage for the

optimal inconsistency characterization problem. As

it is going to be showed, the result of the diagnosis

process is the identification of the rules that cause

the inconsistencies in the rule set and for each one,

the set of the rules which they are inconsistent with.

Each of these sets and their corresponding identified

conflicting rule can be taken as input to the

characterization part of the process, resulting in an

effective computational complexity reduction

(solving several small combinatorial problems is

faster than solving a big one). However, recall that

as the optimal identification of inconsistent rules is a

combinatorial problem, the application of an optimal

characterization algorithm to the result of the

proposed heuristic diagnosis process is senseless. In

contrast, heuristic characterization algorithms

(Pozo4, 2008) can be used, with a heavy

improvement in computational complexity of the

full process.

In this section, two algorithms which implement

Definition 2.1 and the diagnosis process explained in

the previous section are presented. Algorithms are

capable of handling ranges in all selectors.

SECRYPT 2008 - International Conference on Security and Cryptography

434

3.1 Stage 1. Detection of Inconsistent

Pairs of Rules

The first stage of the process detects the inconsistent

rules of the rule set and returns an Inconsistency

Graph (IG, Definition 3.1) representing their

relations. Note that the detection process, like

Definition 2.1, is order independent. Also note that

the presented algorithm is complete, as it

implements Definition 2.1 (which is complete).

Definition 3.1. Inconsistency Graph, IG. An IG is

an undirected, cyclic and disconnected graph whose

vertices are the inconsistent rules of the rule set, and

whose edges are the inconsistency relations between

the these rules. Note that |IG| is the number of

inconsistent rules in RS, and ||IG|| corresponds with

the number of inconsistencies pairs of rules in RS, or

simple the number of inconsistencies in RS.

() ,1 (, )

() , ,1, , (,, )

Let , be an undirected, cyclic and disconnected graph

ij ij

V IG R RS i n Inconsistent R RS

E IG R R V i j n i j Inconsistent R R RS

IG V E

•=∈ ≤≤

=∈≤≤≠•

=< >

Algorithm 1 presented in Figure 7 (implemented

in Object Oriented paradigm and using abstract data

types) exploits the order independence of the

inconsistency definition and only checks

inconsistencies between rules with different actions,

dividing the ACL in two lists, one with allow rules

and the other with deny ones. The algorithm receives

two rule sets. One of them is composed of allow

rules and the other of deny rules of the original rule

set. This decomposition is a linear complexity

operation. The algorithm takes one of the rule sets

and, for each rule, it checks if there is an

inconsistency with other rules in the other one. As

all inconsistencies can be decomposed in two by two

relations, there is no need to check combinations of

more than two rules. Each time the algorithm finds

an inconsistency between a pair of rules, the two

rules are added as vertices to the IG, with a non

directed edge between them. The algorithm returns

an IG. Since all possibilities have been checked,

Algorithm 1 detects of all possible inconsistent rules

(i.e. it is complete). Fig. 8 presents the resulting IG

of the Table 1 example.

Time complexity of Algorithm 1 is bounded by

the two nested loops (lines 8 and 10). Each rule in

ruleSetAllow is tested for inconsistency against rules

in ruleSetDeny. The worst case for the loop is

reached when ruleSetAllow.size()=

ruleSetDeny.size() (i.e. half rules allow and the other

half deny), and the best case when

ruleSetAllow.size()=n and ruleSetDeny.size()=0 or

ruleSetAllow.size()=0 and ruleSetDeny.size()=n.

Thus, the complexity of the improved detection

algorithm depends on the percentage of allow and

deny rules over the total number of rules.

Algorithm 1. Inconsistency Detection algorithm

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

Func detection(in List: ruleSetAllow,

ruleSetDeny; out Graph: ig)

Var

Rule ri, rj

Integer i, j

Alg

for each j=1..ruleSetAllow.size() {

rj= ruleSetAllow.get(j)

for each i=1..ruleSetDeny.size() {

ri = ruleSetDeny.get(i)

if (inconsistency(ri, rj)) {

ig.addVertex(ri)

ig.addVertex(rj)

ig.addEdge(ri, rj)

}

End Alg

// Implements the Inconsistency Definition

Func inconsistency(in Rule: rx, ry; out

Boolean: b)

Var

Integer i

Alg

b = true

i = 1

while (i<=rx.selectors.size() AND b)

b = b AND intersection(rx.getSelector(i),

ry.getSelector(i))

i=i+1

}

End Alg

Figure 7: Inconsistency detection algorithm.

However, there are other inner operations that

should be analyzed in lines 12 to 15. The first one, in

line 12, is inconsistency() which is composed of an

iteration. This operation implements the

inconsistency definition. In typical firewall ACLs,

k=5, and thus the iteration runs 5 times. Anyway,

the iteration is bounded by the number of selectors,

which is a constant, k.

In addition, inside the iteration there is an

intersection between each selector (lines 28 to 30).

The typical 5 selectors of firewall ACLs (Table 1)

are integers or ranges of them, except IP address.

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

435

Knowing if two ranges of integers intersect can be

done in constant time with a naïve algorithm which

compares the limits of the intervals. Knowing if two

IP addresses intersect can also be easily done in

constant time by comparing their network addresses

and netmasks. Other operations of the inner loop

(lines 12 to 14) are the graph-related ones. If the

graph is based on hash tables, vertex and edge

insertions run in constant time, except in some cases

where rehashing could be necessary.

Figure 8: Inconsistency graph.

For all these reasons, the complexity of the two

nested loops is only affected by a constant factor in

all cases, which depends on the constant number of

selectors, k. Thus, worst case time complexity of the

detection algorithm is in O(n

), best case is in O(n),

and average case is in O(n·m) with the number of

allow rules, n, and deny rules, m in the ACL.

Space used by Algorithm 1 is the sum of the

space needed to store the ACL, and the one needed

for the graph. In best case the graph would have n

vertices and n-1 edges. In the worst case, there could

be n-1 inconsistent rules and also n-1 edges per

vertex. Note that the space needed to store an edge is

fewer than the needed to store a vertex, since only a

reference between vertices is needed.

3.2 Stage 2. Detection of Inconsistent

Pairs of Rules

The second and last stage of the diagnosis process

identifies the rules that cause the inconsistencies

from the set of inconsistent pairs of rules (the result

of the previous stage) with an heuristic algorithm.

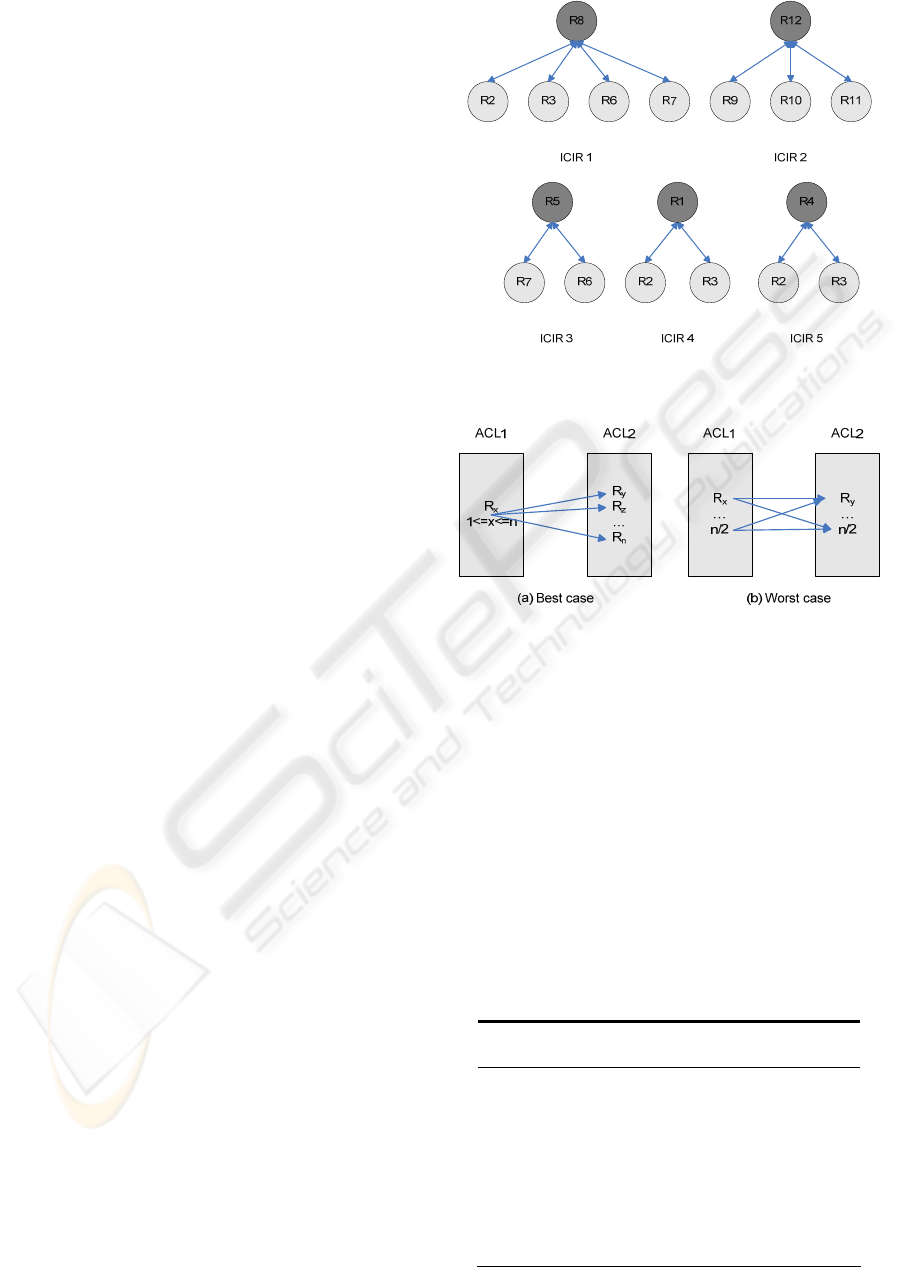
Algorithm 2 (Fig. 9) was initially presented in

(Pozo, 2008). It receives the IG as input and takes

iteratively the vertex with the greatest number of

adjacencies (lines 6 and 7), that is, the vertex with

the greatest number of inconsistencies, v. Then, an

independent cluster of inconsistent rules (ICIR,

Definition 3.2) is created as a tree with v (the

conflicting rule of the cluster) as its root, and its

adjacents (the inconsistent rules) as leafs (lines 8 to

12). The root of all ICIRs from the Diagnosis Set

(DS, Definition 3.3), or the set of rules that must be

removed to get a consistent rule set. Then, v and its

edges are removed from the IG (line 13). If vertices

with no edges are left in the IG, then these vertices

are removed (line 14), since they are consistent by

definition (they are rules with no relations with

others). As inconsistencies have been decomposed in

pair wise relations, ICIRs are always formed by two

levels. For the analyzed example, the algorithm

finishes with a diagnosis set of cardinality five

(|DS|=5), containing the rules DS={R8, R12, R5, R1,

R4}, which are the ICIR roots or the rules that cause

an inconsistency with other ones. If all rules of DS

are removed, the resulting rule set is consistent. R8

and R12 were the most conflicting ones . A trace of

the different iterations of Algorithm 1 when applied

to Table 1 was presented in (Pozo, 2008).

Algorithm 2. Inconsistent Rule Identification algorithm

10.

11.

12.

13.

14.

15.

16.

Func identification(in Graph:ig; out List of

Tree:icirs)

Var

Tree icir

Alg

while (ig.hasVertices()) {

Vertex v = ig.getMaxAdjacencyVertex();

List adj = ig.getAdjacents(v)

icir.createEmptyTree()

icir.setRoot(v)

icir.addChildren(adj)

icirs.add(icir)

ig.removeVertexWithEdges(v)

ig.removeNotConnectedVertices()

}

End Alg

Figure 9: Inconsistency identification algorithm.

Definition 3.2. Independent Cluster of

Inconsistent Rules, ICIR. An ICIR(root, CV) is a

two level tree, rooted in the rule root and where CV

is a set of rules (its leafs). It represents a cluster of

mutually consistent rules, CV, which are at the same

time inconsistent with their root. ICIR(root) is the

rule which has the greatest number of

inconsistencies with other rules of the same cluster.

SECRYPT 2008 - International Conference on Security and Cryptography

436

Note that the action ICIR(root) is the contrary of the

actions of all of its leafs in CV.

(,)

,, (,)

ij ij

ICIR root CV

R CV Inconsistent root R

R CV i j Inconsistent R R

⇔

∀∈ • ∧

∀∈≠•¬

Definition 3.3. Diagnosis Set, DS. This is the set of

rules that cause the inconsistencies, and coincide

with the root of all ICIRs.

{

}

{}

,...,

(),..., ()

Let

e the set of all ICIR of a given , then

ICIR ICIR

DS ICIR root ICIR root

ICIRS

If the rules from the DS are directly removed

from the rule set, it gets consistent. Note that this

heuristic is not necessarily minimal.

Time complexity of Algorithm 2 is bounded by

the loop of line 5, which runs as many times as

ICIRs are formed (it corresponds with the cardinality

of the Diagnosis Set, |DS|). The worst case is

reached, as in Algorithm 1, when

ruleSetAllow.size()=ruleSetDeny.size()=n/2 (Fig.

11(b)), resulting in a |DS|=n/2. In this case,

getMaxAdjacencyVertex() (line 7), a maximum

calculus, runs in O(n) with the number of vertices of

the graph (the number of inconsistencies).

Operations of lines 8, 9, 10, 11, and 12 run in

constant time. removeVertexWithEdges() (line 13)

runs in linear time with the cardinality of its

adjacency list (n/2-1 in the worst case). Finally,

removeUnconnectedVertices() (line 14) is also linear

with the number of vertices in the graph at each

iteration, O(n). Thus, the resulting worst case time

complexity of Algorithm 2 is in O(|DS|·(n+n/2-

1+n))=O(n/2·n)=O(n

The best case is reached, as in Algorithm 1,

when ruleSetAllow.size()=n and

ruleSetDeny.size()=0 or vice versa (Fig. 11(a)). The

IG only has one vertex, v, connected to all the other

vertices. In this case, |DS|=1 and the algorithm is in

O(n). In an average case the algorithm is in

O(|DS|·h), |DS|<<h (h is the number of

inconsistencies).

Algorithm 2 needs some space to store the

ICIRs. Each ICIR needs space for its root and for the

conflictive rules. But note that, as the algorithm is

creating the ICIRs, the corresponding vertices and

edges are removed from the IG, and thus at each

iteration only the space to store the adjacency list of

the removed vertex is necessary. Complexities are

presented in Table 2.

Figure 10: Generated ICIRs and the Diagnosis Set.

Figure 11: Identification best and worst cases.

The result of the diagnosis process is the set of all

ICIRs. As each ICIR represent a different

independent inconsistency, exhaustive search

optimal characterization algorithms can be applied

to each one independently, reducing the effective

computational complexity of the whole process. In

addition, heuristic characterization algorithms can

also be applied (Pozo4, 2008) Also note that the

presented proposal makes no assumptions about how

selector ranges are expressed. This is important,

because if the original rule set is directly used by

algorithms, inconsistency results are given over the

original, unmodified rule set.

Table 2: Detection and Identification Time Complexities.

Number of

inserted rules

Best

case

Average

case

Worst

case

Space

Worst

Detection O(n) O(n·m) O(n

)

Rules·h

Edges

Identification O(n)

O(|DS|·h),

|DS|<<h

O(n

)

Rules·h

Edges

Combined

(Diagnosis)

O(n) O(n·m) O(n

)

Rules·h

Edges

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

437

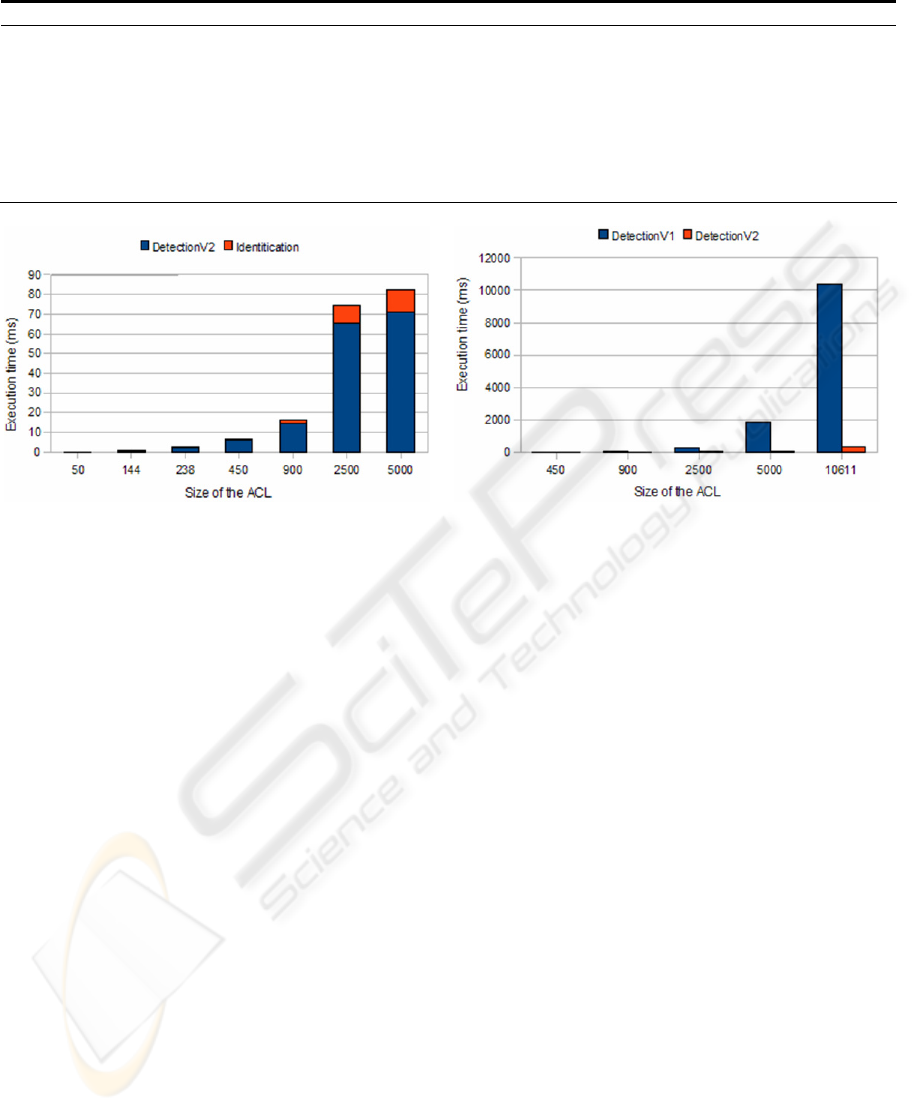
Table 3: Performance Evaluation.

Size %Deny |DS| Average ICIR size #Inconsistencies Detection (ms) Identification (ms) TOTAL (ms)

50 28,21 0 n/a 0 0,06 0 0,06

144 30,91 3 16 48 0,59 0,21 0,8

238 66,43 15 19 291 2,08 0,15 2,23

450 34,73 15 20 312 5,59 0,16 5,75

900 14,8 29 34 1005 13,38 0,64 14,02

2500 6,97 100 43 4337 59,48 4,08 63,56

5000 1,98 32 19 1388 63,93 1,18 65,11

10611 2,05 156 59 18894 346,58 24,79 371,37

Figure 12(a): Running time. Average case Figure 12(b): Comparison between detection algorithms.

3.3 Experimental Results

In absence of standard rule sets for testing, the

proposed heuristic process has been tested with real

firewall rule sets (Table 3). The first column

represents the size of the rule set; the second one the

percentage of deny rules over the rule set size; the

third the cardinality of the Diagnosis Set, |DS|, (or

the number of generated ICIRs), or the

combinatorial problems to be solved by an optimal

characterization algorithm; the fourth represents the

average size of each ICIR (that is, the number of

ICIRs divided by |DS|), or the average size of the

characterization problems to be solved (how many

rules are in them); the fifth the number of

inconsistencies; and the sixth, seventh and last

columns the execution time of the detection,

identification and the sum of them.

The conducted performance analysis represents a

wide spectrum of cases, with ACLs of sizes ranging

from 50 to 10600 rules, and percentages of allow

and deny rules ranging from 2% to 65%. Recall that

worst case for the improved detection algorithm is

half rules allow and the other half deny. Also note

that real ACLs have some important differences with

synthetically generated ones. The most important

one is the number of deny and allow rules: as real

firewall ACLs are usually designed with deny all

default policy, most rules are going to have allow

actions. In ACLs designed with allow all policy,

most rules would have deny actions. Also note that,

as the percentage of allow or deny rules decrease,

the number of inconsistencies does necessarily not,

because the number of inconsistencies depend on

how many rules with different actions intersect. The

result is that the worst case would not normally

happen in real firewall ACLs. Experiments were

performed on a Java implementation with Sun JDK

1.6.0_03 64-Bit Server VM, on an isolated HP

Proliant 145G2 (AMD Opteron 275 2.2GHz, 2Gb

RAM DDR400). Execution times are in ms. Tests

have been run without wildcard rules (RW, deny all

or allow all rules) because WR provide no useful

information to the diagnosis process: they are

conflictive by definition with all rules with the

contrary action.

The experimental comparison of the efficiency of

the proposed algorithms with others of the reviewed

in the bibliography is a very difficult task for two

main reasons. In one hand, there are no standard rule

sets to be used. In other hand different algorithms

cover different parts of the process. One of the most

important parts of the presented experimental

analysis is the average reduction of the full problem,

and the size of each reduced part. Recall that optimal

characterization algorithms can be applied now to

each of these problems and solve them faster than

running the characterization over the full rule set.

SECRYPT 2008 - International Conference on Security and Cryptography

438

Unfortunately, there are neither standardized rule

sets nor syntactic generation tools that can be used to

test how near is the proposed heuristic to the

optimum.

As Table 3 and Fig. 12(a) show, execution time

for the diagnosis process is very reasonable, even in

large rule sets. Note that rule set of sizes 238 and

450 are very near worst case. Rule set of size 10611

has not been represented to prevent image scale

distortion, but note that even with a very high

number of inconsistencies (18894) execution time of

the full process is 371ms. Take into account that a

rule set of 10611 rules is a very big one (Taylor,

2005). Fig. 12(b) presents a comparison between the

previous detection algorithm (Pozo, 2008) and the

one presented in this paper. Note how the previous

version (DetectionV1) (Pozo, 2008) scale

quadratically with the number of rules. However, the

complexity of the new algorithm (DetectionV2)

depends on the percentage of allow and deny rules.

As can be seen, there is a huge difference with real

rule sets.

Figure 13: Identification with and without wildcard rules.

Fig. 13 represents a comparison of running times

of the identification algorithm with and without

wildcard rules, in order to highlight the impact these

rules have in processing time. As we previously

noted, leaving trailing wildcard rules for diagnosis

purposes gives no useful information to the process,

since they are conflictive with all rules with contrary

action.

Other important things worth noting are the

related with problem reduction. The average ICIR

size in Table 3 (fourth column) represents the

average number of children of each generated ICIR

(the number of ICIRs is represented in the third

column as the size of the Diagnosis Set, |DS|). That

is, |DS| is the number of characterization problems to

be optimally solved if optimal characterization

algorithms are going to be used, and Average ICIR

Size is their average size. Clearly, solving (optimally

or not) such small number of small problems is

faster than solving a big combinatorial one.

Finally, due to its low computational complexity,

the presented detection algorithm can be used with

very big rule sets or even in resource constrained

devices (Pozo2, 2008) in a real time process.

4 RELATED WORKS

The closest works to ours are related with

consistency detection in general network filters. In

the most recent work, Baboescu et al. (Baboescu,

2003) provide algorithms to detect inconsistencies in

router filters that are 40 times faster than O(n

) ones

for the general case of k selectors per rule. Although

its algorithmic complexity is not given, it improves

other previous works (Hari, 2000), (Eppstein, 2001).

However, they preprocess the rule set and convert

selector ranges to prefixes, and then apply the

algorithms. This imposes the implicit assumption

that a range can only express a single interval, which

is true (pozo3, 2008). However, the range to prefix

conversion technique could need to split a range in

several prefixes (Srinivasan, 1998) and thus the final

number of rules could increase over the original rule

set. Thus, results are given over the preprocessed

rule set, which could be bigger and different from

the original one.

Other researchers apply brute force,

combinatorial algorithms for the characterization

problem. Thus, the resulting worst case time

complexity will be exponential in all these proposed

algorithms. One of the most important advances was

made by Al-Shaer et al. (Al-Shaer, 2004), where

authors define an inconsistency model for firewall

ACLs with 5 selectors. They give a combined

algorithm to diagnose and characterize the

inconsistencies between pairs of rules. In addition,

they use rule decorrelation techniques (Luis, 2002)

as a pre-process in order to decompose the ACL in a

new, bigger, one with non overlapping rules. Results

are given over the decorrelated ACL, which has the

disadvantages commented above. Although the

proposed characterization algorithm proposed by Al-

Shaer is polynomial, a decorrelation pre-process

imposes a worst case exponential time and space

complexity for the full process.

A modification to their algorithms was provided

by García-Alfaro et al. (García-Alfaro, 2007), where

they integrate the decorrelation and characterization

algorithms of Al-Shaer, and generate a decorrelated

and consistent rule set. Thus, due to the use of the

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

439

same decorrelation techniques, this proposal also has

worst case exponential complexity. The resulting

ACL is also bigger and different from the original

one. However, García-Alfaro et al. provide a

characterization technique with multiple rules.

A similar approach to García-Alfaro was

followed in (Abedin, 2006), where authors provide

worst case O(2

) time complexity algorithms with

the number of rules (they also use rule decorrelation

techniques).

Ordered Binary Decision Diagrams (OBDDs)

have been used in Fireman (Yuan, 2006), where

authors provide a diagnosis and characterization

technique with multiple rules. A very important

improvement over previous proposals is that they do

not need to decorrelate the ACL, and thus, results

are given over the original one. Note that the

complexity of OBDD algorithms depends on the

optimal ordering of its nodes, which is a NP-

Complete problem (Bollig, 1996). This results in a

worst case O(2

) time complexity with the number

of rules, as other proposals.

There are several differences of our work with

these ones. In one hand, we provided an analysis of

the consistency diagnosis problem in rule sets,

separating diagnosis (detection and identification)

from characterization, which enabled us to design

heuristic polynomial diagnosis algorithms. The

result of the diagnosis process is several independent

clusters of inconsistencies, where optimal

characterization algorithms can be applied,

effectively reducing the computational complexity

(in time and space) of the whole process. In addition,

heuristic characterization algorithms can also be

applied. This heuristic process provides an

alternative to the reviewed brute force algorithms for

big rule sets. However, characterization algorithms

are not the focus of the paper, but the presentation of

a novel process and diagnosis algorithms for the

diagnosis part of the process. Our diagnosis

algorithms have a theoretical best case O(n) and

worst case O(n

) time complexity with the number

of rules in the rule set, n. More precisely, the

complexity of our algorithms depends on the

percentage of allow and deny rules over the total

number of them (in the case of detection), and on the

cardinality of the minimal diagnosis set and the

number of inconsistencies (in the case of

identification). Our process is capable of handling

full ranges in all selectors, and does not need to

decorrelate or do any range to prefix conversion to

the ACL as a pre process to the algorithms. We think

that for a result to be useful for a user, it should be

given over the original ACL. However, our proposal

does not cope with redundancies, because we

redundancies are not a consistency problem.

5 CONCLUSIONS

We have deeply analyzed the consistency diagnosis

problem in firewall ACLs, and decided to divide the

consistency management process in three sequential

stages: detection, identification, and

characterization. Inconsistency detection is a

polynomial problem, but minimal identification and

characterization are combinatorial ones. Detection

plus identification is called diagnosis. All reviewed

proposals deal with the full characterization problem

with brute force algorithms, with yield unusable

results for real-life, big rule sets.

In this paper we take a different approach, isolating

the combinatorial parts of the full problem (optimal

identification and characterization) from the

polynomial one (detection). We have proposed an

abstract definition of inconsistency that covers all

previously characterized cases in the bibliography.

Based on this definition, we revisited the

consistency problem in firewall rule sets and showed

that all relations between more than two rules can be

decomposed in simpler pair wise relations.

We have proposed two polynomial algorithms

that should be applied sequentially to get a diagnosis

of the inconsistent rules in the rule set. The first one

detects the inconsistent rules and is complete. The

second one identifies the rules that cause the

detected inconsistencies, and is based in a heuristic.

The diagnosis can then be taken as input to optimal

characterization algorithms resulting in an effective

computational complexity reduction (solving several

small combinatorial problems is faster than solving

one big one), or to heuristic ones.

A theoretical complexity analysis has been done

and showed that the full process has best case O(n)

and worst case O(n

) time complexity with the

number of rules in the rule set, n. An experimental

performance evaluation with real rule sets of

different sizes was also presented, showing that real

rule sets are very near to the best case, and the

effective problem reduction. Unfortunately, there are

neither standardized rule sets nor syntactic

generation tools that can be used to test how near is

the proposed heuristic to the optimum. We

compared our proposal with other works in the

bibliography and showed that, to the best of our

knowledge, no proposals that split the consistency

management process have been made. Thus, our

work represents a completely different way to treat

SECRYPT 2008 - International Conference on Security and Cryptography

440

the problem with algorithms that are useable with

real-life, big rule sets. We have implemented the

algorithms in Java language in a tool which is

available under request.

However, our approach has some limitations that

give us opportunities for improvement in future

works. The most important one is that our process

can diagnose inconsistent rules, but cannot diagnose

redundant rules.

ACKNOWLEDGEMENTS

This work has been partially funded by Spanish

Ministry of Science and Education project under

grant DPI2006-15476-C02-01, and by FEDER

(under ERDF Program). Many thanks to Pablo Neira

Ayuso for providing us with real rule sets for testing

and to the anonymous reviewers for their useful

comments.

REFERENCES

Abedin, M., Nessa, S., Khan, L., Thuraisingham, B.

“Detection and Resolution of Anomalies in Firewall

Policy Rules”. Proceedings of the Annual IFIP

Working Conference on Data and Applications

Security (DBSec), LNCS 4127. Sophia Antipolis,

France, 2006.

Al-Shaer, E., Hamed, H. Modeling and Management of

Firewall Policies". IEEE eTransactions on Network

and Service Management (eTNSM) Vol.1, No.1, 2004.

Baboescu, F., Varguese, G. “Fast and Scalable Conflict

Detection for Packet Classifiers.” Elsevier Computers

Networks (42-6) (2003) 717-735.

Bollig, B., Wegener, I. “Improving the Variable Ordering

of OBDDs is NP-Complete”. IEEE Transactions on

Computers, Vol.45 No.9, September 1996.

Eppstein, D., Muthukrishnan, S. “Internet Packet Filter

Management and Rectangle Geometry.” Proceedings

of the Annual ACM-SIAM Symposium on Discrete

Algorithms (SODA), January 2001.

García-Alfaro, J., Boulahia-Cuppens, N., Cuppens, F.

Complete Analysis of Configuration Rules to

Guarantee Reliable Network Security Policies,

Springer-Verlag International Journal of Information

Security (Online) (2007) 1615-5262.

Hamed, H., Al-Shaer, E. "Taxonomy of Conflicts in

Network Security Policies." IEEE Communications

Magazine Vol.44, No.3, 2006.

Hari, B., Suri, S., Parulkar, G. “Detecting and Resolving

Packet Filter Conflicts.” Proceedings of IEEE

INFOCOM, March 2000.

Luis, S., Condell, M. "Security policy protocol." IETF

Internet Draft IPSPSPP-01, 2002.

Pozo, S., Ceballos, R., Gasca, R.M. “Fast Algorithms for

Consistency-Based Diagnosis of Firewalls Rule Sets.”

International Conference on Availability, Reliability

and Security (ARES), Barcelona, Spain. IEEE

Computer Society Press, March 2008.

Pozo2, S., Ceballos, R., Gasca, R.M. "Fast Algorithms for

Local Inconsistency Detection in Firewall ACL

Updates". 1

International Workshop on

Dependability and Security in Complex and Critical

Information Systems (DEPEND). Cap Esterel, France.

IEEE Computer Society Press, 2008.

Pozo3, S., Ceballos, R., Gasca, R.M. "AFPL, An Abstract

Language Model for Firewall ACLs". 8

International

Conference on Computational Science and Its

Applications (ICCSA). Perugia, Italy. Springer-

Verlag, 2008.

Pozo4, S., Ceballos, R., Gasca, R.M. "Polynomial

Heuristic Algorithms for Inconsistency

Characterization in Firewall Rule Sets". 2

International Conference on Emerging Security

Information, Systems and Technologies

(SECURWARE). Cap Esterel, France. IEEE

Computer Society Press, 2008.

Srinivasan, V., Varguese, G, Suri, S., Waldvogel, M. “Fast

and Scalable Layer Four Switching.” Proceedings of

the ACM SIGCOMM conference on Applications,

Technologies, Architectures and Protocols for

Computer Communication, Vancouver, British

Columbia, Canada, ACM Press, 1998.

Taylor, David E. Survey and taxonomy of packet

classification techniques. ACM Computing Surveys,

Vol. 37, No. 3, 2005. Pages 238 – 275.

Yuan, L., Mai, J., Su, Z., Chen, H., Chuah,, C. Mohapatra,

P. FIREMAN: A Toolkit for FIREwall Modelling and

ANalysis. IEEE Symposium on Security and Privacy

(S&P’06). Oakland, CA, USA. May 2006.

Wool, A. A quantitative study of firewall configuration

errors. IEEE Computer, 37(6):62-67, 2004.

A HEURISTIC POLYNOMIAL ALGORITHM FOR LOCAL INCONSISTENCY DIAGNOSIS IN FIREWALL RULE

SETS

441