A 640 MBIT/S 32-BIT PIPELINED IMPLEMENTATION OF THE AES

ALGORITHM

Guido Marco Bertoni

, Luca Breveglieri

, Roberto Farina

and Francesco Regazzoni

ST Microelectronics, Agrate Briaznza, Italy

Politecnico di Milano, Milano, Italy

CEFRIEL - Politecnico di Milano, Milano, Italy

ALaRI, University of Lugano, Lugano, Switzerland

Keywords:

AES, Cryptographic coprocessors.

Abstract: Due to the diffusion of cryptography in real time applications, performances in cipher and decipher operations

are nowadays more important than in the past. On the other side, while facing the problem for embedded

systems, additional constraints of area and power consumption must be considered. Many optimized software

implementations, instruction set extensions and co-processors, were studied in the past with the aim to either

increase performances or to keep the cost low. This paper presents a co-processor that aims to be an inter-

mediate solution, suitable for such applications that require a throughput in the Megabit range and where the

die size is a bit relaxed as constraint. To achieve this goal, the core is designed to operate at 32 bits and the

throughput is guaranteed by a 2 stage pipeline with data forwarding. The obtained results synthesizing our

coprocessor by means of the CMOS 0.18 µm standard cell library show that the throughput reaches 640 Mbit/s

while the circuit size is of only 20 K equivalent gates.

1 INTRODUCTION

With the diffusion of cryptography in embedded ap-

plications, the need of performance started to be con-

tradictory with respect to the stricter constraints of

low power consumption and low area required by

such domain. In fact, while for high-end applications

the most important constraint is throughput, it is not

so for embedded applications which do not require

real time cryptography but instead a throughput rate

in the Megabit range. For these applications, once a

sufﬁcient level of time performance has been reached

the constraint on time starts relaxing. As a result, it is

neither necessary nor advisable to implement in hard-

ware the whole AES round by means of a full 128-bit

architecture; a much smaller circuit can still fulﬁll the

time performance requirement.

Many approaches were studied in the past to ad-

dress the problems raised by the need of cryptogra-

phy in different application domains, ranging from

optimized software implementation ((Bertoni et al.,

) (Gladman, )) to instruction set extension ((Tillich

et al., 2005), (Fiskiran and Lee, 2005) (Tillich and

Grossschaedl, 2004)) and co-processor ((Feldhofer

et al., 2005) (Kuo and Verbauwhede, 2001) (Oliva

et al., 2003)). Despite this considerable amount of

previous research, only few works were addressed to

propose intermediate solutions, that target the wide

class of embedded systems, where time performance

and area are both constraints but none of them is dra-

matically strict.

In this paper, we propose a 128 bit key AES co-

processor that aims at being used in such applications

that requires to keep the silicon area reasonably low

and where acceptable time performances are needed.

The proposed coprocessor is able to perform both

AES encryption and decryption, and, in order to in-

crease its time performance, it is based on a two-stage

pipeline. Two dedicated register ﬁles are designed

to perform the ShiftRows permutation directly, more-

over, pipeline forwarding is introduced (of one data

byte only), in order to prevent stalls in the pipeline.

The remainder of this paper is organized as fol-

lows. Section 2 reviews some related work. Section 3

summarizes the Rijndael algorithm. Our proposed co-

processor for 128 bit key AES is described in Sec-

453

Marco Bertoni G., Breveglieri L., Farina R. and Regazzoni F. (2008).

A 640 MBIT/S 32-BIT PIPELINED IMPLEMENTATION OF THE AES ALGORITHM.

In Proceedings of the International Conference on Security and Cryptography, pages 453-459

DOI: 10.5220/0001925504530459

 SciTePress

tion 4. Experimental results and comparison with the

state of the art are reported in Section 5. Section 6

concludes the paper presenting our ﬁnal remarks.

2 RELATED WORK

The initial implementations of the Rijndael algorithm

appeared soon during the AES process of the stan-

dard. Afterwards, a large number of different imple-

mentations was published, each of them targeted to

different needs.

In the previous research it is possible to ﬁnd both

software and hardwareimplementations, developedin

order to meet different constraints in terms of sili-

con area, algorithm ﬂexibility, time performance and

power consumption. Most of the research work done

in the hardware direction is related to implementation

in FPGA technology, which has substantially differ-

ent requirements and constraints with respect to the

ASIC technology. For this reason, a comparison of

our work with those related to FPGA implementation

is not possible.

An 8-bit implementation of the AES algorithm

which supports encryption and decryption is de-

scribed by Feldhofer et al. in (Feldhofer et al., 2005).

This implementation, optimized for low-resource re-

quirements, is targeted to the RFID application do-

main and is based on a 8-bit architecture. The

standard-cell implementation requires roughly 3400

equivalent gates, while the maximum clock frequency

of 80 MHz allows a data throughput rate of 9.9 Mbit

/ s.

In (Satoh et al., 2000) a compact and high-speed

architecture for 128-bit key AES is presented. Sep-

arated function blocks are developed for encryption,

decryption and key scheduling. The SubBytes trans-

formation is performed by four S-Box modules de-

signed for composite ﬁeld arithmetic, which are com-

mon to the encryption round and the key schedul-

ing. Using the CMOS 0.11 µm VLSI technology, this

module can reach a throughput of 311 Mbit/s, while

the hardware complexity is of 5, 400 equivalent gates.

The architecture operates at 32 bits.

Paper (Mangard et al., 2003) presents a highly

regular and scalable AES 32-bit hardware architec-

ture, for supporting encryption, decryption, various

key sizes and the CBC mode. The architecture is a

matrix of 16 cells, which operate at 8 bits to calcu-

late the MixColumns transformation and all the other

ones, except the SubBytes. The number of S-Boxes is

customizable, and in their paper the authors show that

the highest reached throughput is 241 Mbit/s, while

the implementation requires 15 K equivalent gates.

Paper (Chodowiec and Gaj, 2003) presents a com-

pact FPGA architecture for the AES algorithm with

a key of 128 bits. Encryption, decryption and key

schedule are all implemented using limited resources.

This implementation can encrypt and decrypt data

streams of 150 Mbit / s. The architecture exploits spe-

ciﬁc features of the target FPGA, and the implemen-

tation of the MixColumns and the InvMixColumns

transformations allows to share part of the circuit be-

tween the two operations.

In (Hodjat and Verbauwhede, 2006) a high per-

formance AES processor is presented. With loop

unrolling and outer-round pipelining techniques, a

throughput of 30 Gbit / s to 70 Gbit / s is achievable

by means of a CMOS 0.18 µm VLSI technology. The

architecture proposed in the paper uses an inner round

pipelining scheme of the composite ﬁeld implementa-

tion of the S-Box, and uses an off-line key scheduling.

Paper (Kuo and Verbauwhede, 2001) discusses the

architectural optimization of an AES processor. Par-

allelism and distributed memory are exploited in or-

der to reach a throughput of 1.82 Gbit / s for data

encryption. The required silicon area is of 173, 000

equivalent gates.

Paper (Hsiao et al., 2006) exposes traditional

hardware design methods and introduces a tech-

nique for area optimization. The presented Common-

Subexpression-Elimination (CSE) algorithm is ap-

plied to the subfunctions that realize the various trans-

formations in the AES encryption and decryption.

The paper claims that a cell-based implementation of

the proposed AES design can achieve an area reduc-

tion rate of about 20% with respect to using the well-

known Synopsys VLSI design tools.

A comprehensive survey can be found in (Feld-

hofer et al., ), where different hardware implementa-

tions that target various applications are presented.

3 THE ALGORITHM

In this section we give an overview of the Rijndae-

lalgorithm, that became ofﬁcially AES after the pub-

lication of (Institute of Standards and Technology

(NIST), 2001), on the 26th of November 2001. As

requested by NIST, the algorithm implements a block

cipher for symmetric key cryptography and supports

a key size of 128, 192 and 256 bits, while the block

size is restricted to 128 bits. Every block is repre-

sented using four 32-bit words. The algorithm works

on a two dimensional representation of the input block

called state, which is initialized with the input data

block, holds the intermediate result during the cipher

and decipher process, and ultimately holds the ﬁnal

SECRYPT 2008 - International Conference on Security and Cryptography

454

result when the process is completed. All the trans-

formations of the algorithm are grouped into a sin-

gle function called round, that is iterated a number of

times which depends on the key size.

The encryption process starts copying the input

block into the state array, and is followed by the

ﬁrst key addition. In the encryption process, the

round function is composed of four different trans-

formations: ShiftRows that cyclically shifts to left the

bytes in the last three rows of the state, with dif-

ferent offsets; SubBytes that is the non-linear byte

substitution and operates independently on each byte

of the state; the MixColumns that multiplies modulo

+ 1 the columns of the state by the polynomial

{03}x

+ {01}x

+ {01}x+ {02}; and ﬁnally the Ad-

dRoundKey, that adds a round key contribute to the

state.

All the needed round keys are generated in the

AES algorithm by the so called key schedule, that

takes the secret key and executes the expansion rou-

tine as speciﬁed in the standard.

The decryption algorithm is similar to the encryp-

tion one and uses the same basic transformations, but

applied on reversed order. The decryption key sched-

ule is identical to that for encryption, but it starts us-

ing the last round key and generates the round keys in

reverse order.

4 IMPLEMENTATION

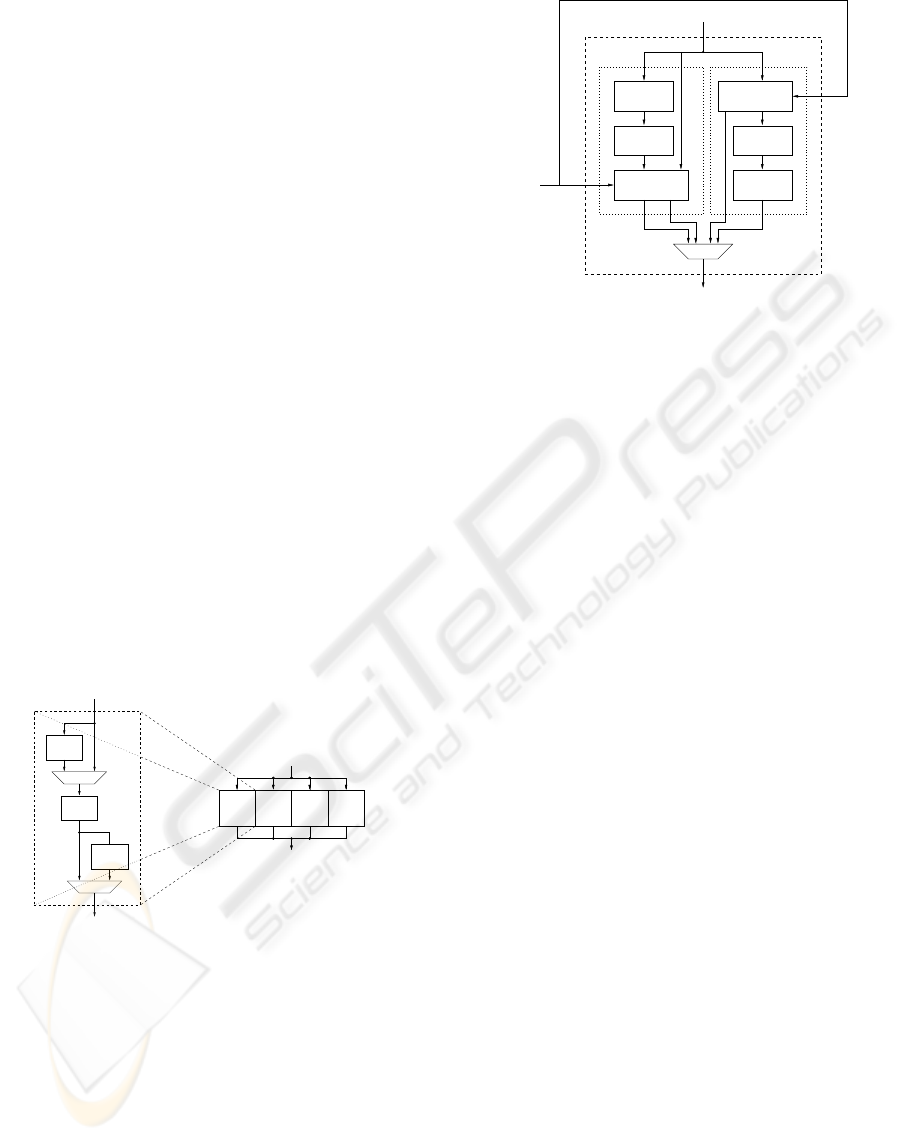
Figure 1 depicts the structure of our AES core. The

proposed accelerator has a pipeline of two stages and

is designed to compute both encryption and decryp-

tion. The state is stored in the registers by columns,

while internally each component works on words of

32 bit.

In order to avoid access conﬂicts, two register ﬁles

for storing the intermediate states are needed. The

second register ﬁle is also the place where the output

will be found at the end of the core computation.

The key is unrolled on-the-ﬂy by the dedicated

module KeySched, which supports a key of 128 bits.

This is not believed to be a limitation, since most of

the hardware AES implementations nowadays sup-

ports only this key size. Furthermore, this is a dedi-

cated module, which can be modiﬁed to support other

key lengths without implications for the rest of the

core. The key addition step is performed within the

second stage of the pipeline. To allow the module to

process further blocks of data without inserting stalls

in the pipeline, a block for the key addition is inserted

uphill one of the register ﬁles: this allows computing

the ﬁrst round on the next data block while complet-

ing the manipulation of the current one.

4.1 The ShiftRows Transformation

In the proposed implementation the state is stored

in the register ﬁles by columns, while the ShiftRows

transformation (and its inverse, too) operates on the

rows. In order to perform the full transformation on

a word in one clock cycle, a mechanism for retriev-

ing the bytes that the transformation is waiting for is

needed. The correct choice is performed by the selec-

tor of Figure 2: by enabling the appropriate input of

the multiplexer, each byte is loaded in the correct po-

sition for building the word needed by the next trans-

formation.

When a register ﬁle plays as input the other rep-

resents the output; in the next round, the role are

exchanged: data are written to the register ﬁle from

32 32

Selection Selection

Input

Xor round key

Output

Buffer

KeySched

ISubWord

SubWord

MixCol+XorK

XorK+IMixCol

Round key

Figure 1: Internal structure of the 32-bit core.

32 32 32 32

8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8

Output word

Figure 2: Byte selection for register ﬁles.

A 640 MBIT/S 32-BIT PIPELINED IMPLEMENTATION OF THE AES ALGORITHM

455

where they were read in the previous round. Because

of this, we provide both register with the same selec-

tion mechanism.

4.2 The S-Box Transformation

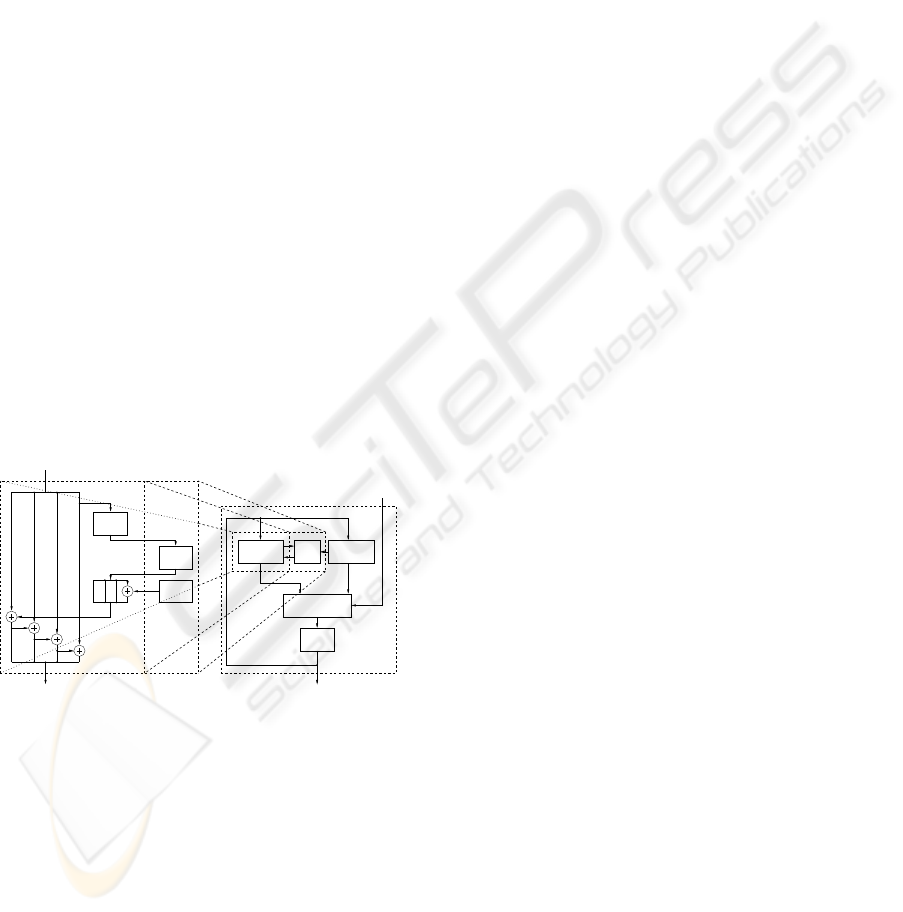
The SubBytes (or S-Box) transformation is performed

on a full word of 32 bits. The SubWord module is ob-

tained by combining four modules of the same kind

that perform the transformation on a byte. Differ-

ent architectures were analyzed and synthesized: in

particular one where the S-Box contents are stored in

look up tables (LUT), and one where the S-Boxes are

calculated. The ﬁnal solution is presented in Figure 3:

the S-Box module performs both the direct and the in-

verse SubBytes transformation. As described in (In-

stitute of Standards and Technology (NIST), 2001),

the transformation is calculated by applying an afﬁne

transformation over GF(2) to the multiplicative in-

verse (in GF(2

)) of the input. Instead, the inverse

afﬁne transformation must be applied before taking

the multiplicative inverse. In the proposed implemen-

tation, both the Afﬁne and the (inverse) IAfﬁne trans-

formations are calculated, while the multiplicative in-

verse is tabulated (block Inverse of Figure 3). This

solution allows to perform both the direct and the in-

verse transformationsusing only four tables, while for

instance in the complete LUT implementation eight

tables are needed.

8 8 8 8

8888

S−box S−box S−box S−box

Output word

Input word

IAffine

Inverse

Affine

Input byte

Output byte

8 8 8 8

8888

S−box S−box S−box S−box

Output word

Input word

Figure 3: Internal structure of the SubWord module.

4.3 The MixColumns and Key Addition

Transformations

The module for the MixColumns transformation has

one column of the state array as input; then for ev-

ery byte the multiplied valuesare producedand xored.

In addition, the key addition step takes place and the

transformed column is output. Figure 4 overviews

the structure of the module: there are two branches,

where the direct and inverse MixColumns are calcu-

lated.

Input word

Direct

MixColumn

module

Inverse

MixColumn

module

Output word

XOR

Round Key

XOR

Round Key

Xtime

Contributes

Addition

Contributes

Addition

IXtime

Figure 4: Overview of the MixCol module.

The XTime component is responsible for produc-

ing the different contributes of the input byte for the

direct MixColumns transformation. This component

calculates the contribute times 2 of the input byte.

By xoring this result with the initial value, the con-

tribute times 3 is obtained, while the initial value itself

represents the contribute times 1. The same mecha-

nism is applied to compute the inverse MixColumns

transformation, where the needed contributes are pro-

duced. After producing all the contributes, they must

be xored in order to obtain the transformed word: to

do so, two different sub-modules are designed. This

is why in Figure 4 two different blocks for contribute

addition are shown. Such modules are responsible

for completing the array calculations: therefore, ev-

ery component consists of four xor modules, and each

of them has four bytes as input and produces a single

byte as result.

The MixColumns module computes the key ad-

dition step too: taking advantage of its double path

structure, the key addition can be performed in the

correct sequence. Further logic is not needed because

of the difference in this step during cipher or deci-

pher operations. Since the MixColumns transforma-

tion must be skipped when computing the ﬁnal round

in cipher operations and during the initial round when

deciphering, mux banks are inserted in both datap-

aths.

4.4 Key Scheduling

Figure 5 shows the module that executes the key

schedule: it produces each round key on-the-ﬂy,

which means that every round key is computed soon

before it is used, and that after being used it is imme-

diately discarded. Such an approach has the advan-

tage of requiring less memory: in fact, the round key

can be stored in four registers, by far fewer than the

forty needed for storing the fully unrolled key. The

SECRYPT 2008 - International Conference on Security and Cryptography

456

on-the-ﬂy method, on the other hand, must be cor-

rectly framed in the sequence of operations, in order

not to slow down the whole co-processor operation.

In the direct key scheduling, the current round key is

obtained from the round key used in the previous en-

cryption round, while for decryption the round keys

must be computed in reverse order. Therefore the key

for step (i+ 1) has to be provided to obtain the key

for step i. This implies a setup phase for decryption,

where the module calculates the last round key. After

doing so, the module works exactly in the same way

as for encryption, and therefore produces on-the-ﬂy

the key contributes for every (inverse) round.

One small look-up table stores the values of the

round constants needed to unroll the key. Since it is

implemented as a look-up table, only one module can

be used in both cipher and decipher operations: the

control unit will produce the indexes to read the cor-

rect value.

The S-Box transformation is computed using the

tabulated modules. This solution is not the smallest

possible in terms of area requirements, but it must be

recalled that the proposed design aims to be an inter-

mediate solution, targeting applications where there

are not very strict constrains in terms of area and a

reasonable throughput is required. Because of this, to

leverage on tabulated S-Boxes for the key unrolling

represents the best possible area/performance trade

off for our target applications.

Secret key INPUT

3232 32

Output round key

Input round key

RotWord

SubWord

RCon

Round key OUTPUT

Buffer

Key selector

128

Direct KS Inverse KS

128

RCon

SubWord

Figure 5: Overview of the KeySched module.

4.5 The Pipeline Stages and the

Forwarding

The ﬁrst stage of the pipeline performs the ShifRows

and the S-Box transformations, using the modules de-

scribed before. The byte selection mechanisms allow

to retrieve the word to work on. The output word

is then processed by the SubWord module, which

performs the non-linear transformation of the whole

word. Two of the byte selection mechanisms must be

used in order to obtain both the direct and the inverse

ShiftRows transformations: two register ﬁles are nec-

essary, which involves a total of four byte selection

blocks. A multiplexer array will be used to propagate

the right word, depending on the operation to execute.

At the end of the S-Box module, a buffer is placed

to break the data path. At this point, the MixColumns

transformation must be executed. This transforma-

tion, however, is skipped during the last round. Con-

sequently, a multiplexer to choose to propagate the

word coming from the previous buffer instead of the

output word of the MixCol module, is inserted. Such

a function block is driven by a control unit, which

generates all the necessary control signals for the

multiplexers. This pipeline stage incorporates both

the MixColumns transformation and the key addition

step, which is performed word by word inside the

MixColumns module, too. In this way, the correct

word is directly written to the second register, com-

pleting the round.

4.5.1 The Forwarding

The top illustration in Figure 6 highlights the word

that must be read from the state array in order to

perform the ShiftRows transformation; other buffers

are initially empty. The round thus starts reading

the word [b

, b

], thanks to the byte selection

mechanism. This word feeds the SubWord module,

and the result is stored into the buffer at the output in

order to cut the data path. The second illustration in

Figure 6 depicts the current situation, the second word

to be read from the state array is highlighted.

In the next clock cycle, the second column,

, b

], is read from the register ﬁle and, after

passing the SubWord module, it is stored into the in-

termediate buffer; the previous one passes through the

MixCol module, and is written into the second register

ﬁle. This produces the ﬁrst column of the new state

array: the key addition step is performed inside the

MixColumns module as described in 4.3.

A further clock cycle causes the third word,

, b

], to be read from the byte selection

blocks; this is processed by the SubWord module and

the result is stored into the buffer. The previous word

passes through the MixCol module and is stored into

the register ﬁle: the second column of the new state

array comes ready. The current situation is depicted

in Figure 6; the fourth word to be read is highlighted,

too.

Again, in the next clock cycle, the third column

passes on the MixCol module and is stored into the

state array; the fourth and last word, [b

, b

is read from the registers and passes the SubWord

A 640 MBIT/S 32-BIT PIPELINED IMPLEMENTATION OF THE AES ALGORITHM

457

module waiting for the MixColumn transformation in

the next step, as shown in Figure 6.

Buffer

Figure 6: Current situation of the buffers.

In the next step the computation of the next round

must avoid inserting bubbles in the pipeline: while the

fourth word is passing through MixCol module, the

SubWord module needs to process the ﬁrst column of

the newly created state array. The situation is shown

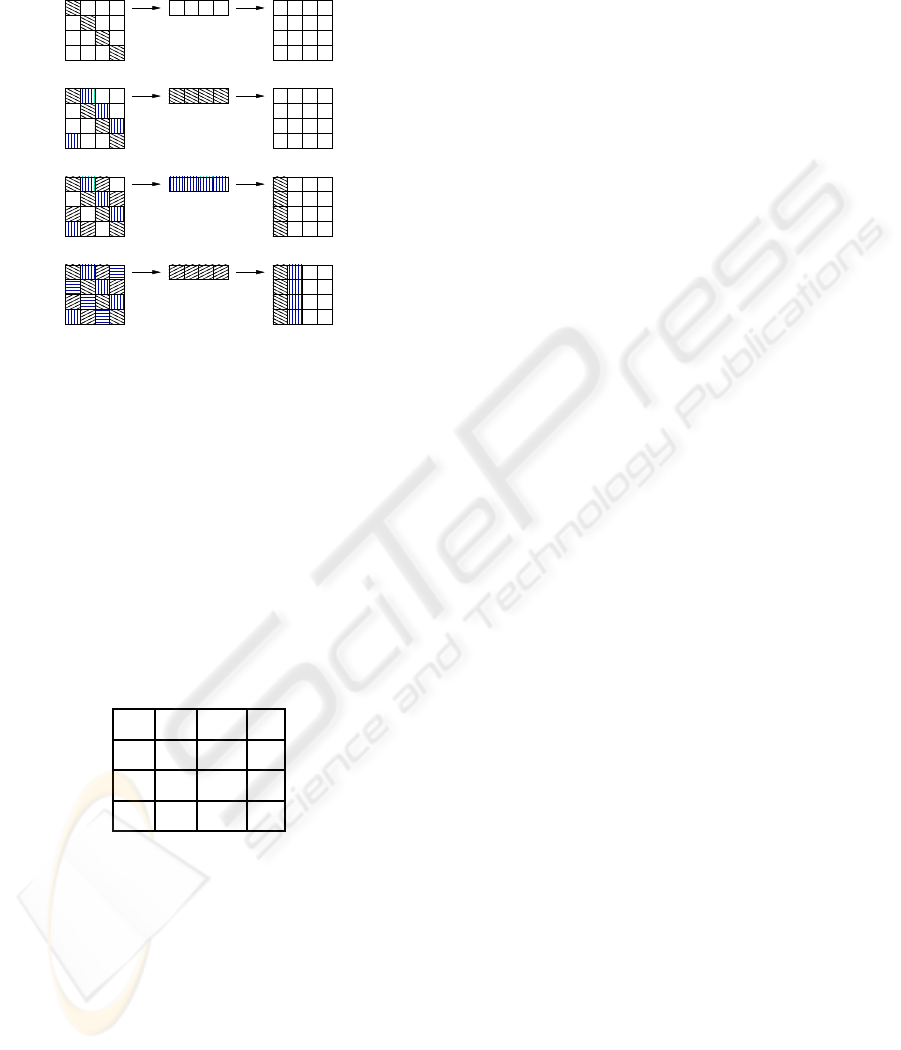
in table 1, where the “X” symbols indicate the bytes

not yet produced, and the “?” symbol underlines the

byte needed to complete the word that will become

the ﬁrst one for the next round computation, consis-

tently with the adopted byte selection mechanism.

Table 1: Status matrix situation when the third word is writ-

ten.

′

In order to respect data dependencies, one pos-

sible solution could be the insertion of a so called

bubble into the pipeline, since when the ﬁrst word

for the next round computation should be read, the

fourth word is not yet written in the register ﬁle. In

this case however,the insertion of the bubble degrades

performances, although increases the critical path. In

fact, the additional combinatorial logic needed to for-

ward the missing byte still allows to reach a higher

throughput w.r.t. the insertion of a stall in the pipeline.

Thus, if the resulting missing byte coming from the

MixCol module is forwarded directly to the SubWord

module rather than awaiting the corresponding word

to be written into the register ﬁle, the ﬁrst word be-

comes ready for the next round computation during

the needed step. Note that only the last byte of such

word must be forwarded, because it is the only one

needed to complete the word to start the next round

computation, as indicated in Table 1. No problems

come from the key addition step, since key addition is

directly performed inside of the MixCol module: the

forwarded byte has been already xored with the cor-

rect key contribute.

The decryption process is similar to the encryp-

tion one, except that it requires a setup phase to com-

pletely unroll the key: this allows to retrieve the last

key contributenecessary for the reverse on-the-ﬂy key

unrolling. During the decryption, the transformations

are applied in reverse order; no problem is raised by

the key addition step since the MixColumns module

ensures that the two datapaths correctly perform the

sequence of operations, as shown in Figure 4.

5 RESULTS

To evaluate the proposed AES coprocessor, we have

implemented it in VHDL and then synthesized with

Synopsys Design Compiler (Synopsys Design Com-

piler:, ) using a CMOS 0.18 µm standard cell library.

Our AES coprocessor works properly with a system

clock frequency up to 200 MHz, that corresponds to

a throughput of 640 Mbit/s. The required area is

250056.703125 µm

, which is roughly equivalent to

20 K gates (20, 329).

Table 2 shows the comparison of our implemen-

tation with the state of the art for 32 bits AES copro-

cessors. The functionalists of the above AES com-

pact coprocessors are all are identical and all of them

implement the key schedule on-the-ﬂy. It is possi-

ble to notice that, among the compact VLSI design,

our reaches the highest throughput, which is approx-

imately twice that presented in (Satoh et al., 2000).

Silicon area is, as it could be expected, larger than

that required by the smallest solutions found in the

literature. Note however that, at best that our knowl-

edge, the reached throughput is the highest available

for AES implementation below 20 K gates, therefore,

the proposed solution is very recommendable for ap-

plications requiring Megabit throughput with reason-

able silicon area.

SECRYPT 2008 - International Conference on Security and Cryptography

458

Table 2: Comparison with the state of the art: time and area.

Version Clock Throughput Area Technology

AES MHz Mbps GEs µm

Proposed 200 640 20 K 0.18

Satoh (Satoh et al., 2000) 130 311 5.4 K 0.11

Mangard (Mangard et al., 2003) 64 241 15 K 0.6

6 CONCLUSIONS

In this paper, a coprocessor for implementing the en-

cryption and decryption algorithms of the AES has

been presented. The architecture supports a key size

of 128 bits, operates at 32 bits and is based on a

pipeline of two stages with data forwarding. The

proposed coprocessor has a throughput of 640 Mbit/s

and requires approximately 20 K equivalent gates to

be implemented. The proposed AES coprocessor ex-

hibits the best time performance with respect to the

comparable ones published in the literature, at the

cost of a slightly larger area. We believe that this

implementation is particularly suitable for those ap-

plications that can not stand the cost of a 128 bits im-

plementation, but that still require a relatively high

throughput, such as in the wireless communications.

REFERENCES

Bertoni, G., Breveglieri, L., Fragneto, P., Macchetti, M.,

and Marchesin, S. Efﬁcient Software Implementation

of AES on 32-Bit Platforms. Proceeedings of CHES

2002, 2523:159–171.

Chodowiec, P. and Gaj, K. (2003). Very Compact FPGA

Implementation of the AES Algorithm. Proceedings

of CHES 2003, pages 319–333.

Feldhofer, M., Lemke, K., Oswald, E., Standaert, F.,

Wollinger, T., and Wolkerstorfer, J. State of the art

in hardware architectures. European Network of Ex-

cellence in Cryptology, (2006).

Feldhofer, M., Wolkerstorfer, J., and Rijmen, V. (2005).

AES implementation on a grain of sand. Information

Security, IEE Proceedings, 152(1):13–20.

Fiskiran, A. M. and Lee, R. B. (2005). On-chip lookup ta-

bles for fast symmetric-key encryption. In ASAP ’05:

Proceedings of the 2005 IEEE ASAP, pages 356–363,

Washington, DC, USA. IEEE Computer Society.

Gladman, B. http://fp.gladman.plus.com/.

Hodjat, A. and Verbauwhede, I. (2006). Area-throughput

trade-offs for fully pipelined 30 to 70 Gbits/s AES

processors. IEEE Transactions on Computers,

55(4):366 – 372.

Hsiao, S., Chen, M., and Tu, C. (2006). Memory-free low-

cost designs of advanced encryption standard using

common subexpression elimination for sub-functions

in transformations. IEEETransactions on Circuits and

Systems I, 53(3):615–626.

Institute of Standards, N. and Technology (NIST) (2001).

Announcing the Advanced Encryption Standard

(AES). Federal Information Processing Standards

Publication 197.

Kuo, H. and Verbauwhede, I. (2001). Architectural Opti-

mization for a 1.82 Gbits/sec VLSI Implementation of

the AES Rijndael Algorithm. Proceedings of CHES,

pages 51–64.

Mangard, S., Aigner, M., and Dominikus, S. (2003). A

Highly Regular and Scalable AES Hardware Archi-

tecture. IEEE Transactions on Computers, 52(4):483–

491.

Oliva, D., Buchty, R., and Heintze, N. (2003). AES and the

cryptonite crypto processor. In CASES ’03: Proceed-

ings of the 2003 international conference on Compil-

ers, architecture and synthesis for embedded systems,

pages 198–209, New York, NY, USA. ACM Press.

Satoh, A., Morioka, S., Takano, K., and Munetoh, S. (2000).

A Compact Rijndael Hardware Architecture with S-

Box Optimization. In Proceedings of ASIACRYPT

2001, number 2248 in LNCS, pages 239–254.

Synopsys Design Compiler:.

http://www.synopsys.com/products/logic

Tillich, S. and Grossschaedl, J. (2004). Accelerating AES

Using Instruction Set Extensions for Elliptic curve

Cryptography. In LNCS 3481: Proceedings of the

Computational Science and Its Applications, pages

665–675, Berlin, Germany. Springer Verlag.

Tillich, S., Grossschdl, J., and Szekely, A. (2005). An In-

struction Set Extension for Fast and Memory-efﬁcient

AES Implementation. In CMS 2005:Proceedings of

the Communications and Multimedia Security, pages

11–21, Berlin, Germany. Springer Verlag.

A 640 MBIT/S 32-BIT PIPELINED IMPLEMENTATION OF THE AES ALGORITHM

459