
AN E-VOTING PROTOCOL BASED ON PAIRING BLIND
SIGNATURES
L. L´opez-Garc´ıa, F. Rodr´ıguez-Henr´ıquez
CINVESTAV-IPN, Department of Computing, Av. Instituto Polit´ecnico Nacional No. 2508
Col. San Pedro Zacatenco, D.F. 07300, Mexico
M. A. Le´on-Ch´avez
Benem´erita Universidad Aut´onoma de Puebla, Facultad de Ciencias de la Computaci´on
14 Sur y Av. San Claudio, CP 72570, Puebla, Mexico
Keywords:
e-voting protocols, pairing-based signatures, digital signatures.
Abstract:
In this paper we present a fair e-voting protocol able to guarantee voter’s anonymity and double vote detection.
The main cryptographic building blocks used by our system are two, namely, pairing-based blind signatures
and elliptic curve digital signatures. We give both, a security and a cryptographic cost analysis of our proposed
protocol, showing that it has a computational cost similar to other e-voting schemes previously reported, and
the same time, it provides a good robustness against the potential attacks analyzed in this paper.
1 INTRODUCTION
In an electronic election system, privacy and secu-
rity are mandatory features. However, it is not al-
ways obvious how to achieve these two characteris-
tics at a reasonable price, due to the fact that when
an election process takes place, mechanisms that as-
sure both, security and privacy may be too expen-
sive for system administrators on one side, and in-
convenient for users on the other. In general terms,
the basic properties that an electronic voting system
must fulfill, are Authentication, Fairness, Accuracy,
Integrity, Anonymity, Transparency, Verification and
Accountability (Qadah and Taha, 2006). In this paper
we present an e-voting scheme that uses pairing-based
blind signatures as they were proposed in (Boldyreva,
2003). In order to protect votes’ data integrity we
sign it using an elliptic curve digital signature scheme
(ECDSA) (NIST, 1994). To the best of our knowl-
edge, e-voting schemes using pairing-based blind sig-
natures have not been proposed before.
2 MATHEMATICAL
BACKGROUND
Let us consider an elliptic curve E defined over a fi-
nite field F
p
m
, where p is a prime number and m is
a positive integer and let E(F
p
m
) represent the addi-
tive group of points in E. Let P ∈ E(F
p
m
) be a point
of order n, i.e., P generates a subgroup G
1
of order
n. Then, finding an integer d ∈ [2, n − 1] such that
Q = dP holds, is known as the Elliptic Curve Discrete
Logarithm Problem (ECDLP). For carefully chosen
elliptic curves E, the ECDLP is considered a hard dif-
ficult problem.
The Elliptic Curve Digital Signature Algorithm
(ECDSA), is the elliptic curve analogue of the Dig-
ital Signature Algorithm (DSA) (NIST, 1994). No
subexponential-time algorithm is known for the ellip-
tic curve discrete logarithm problem. For this reason,
the strength-per-key-bit is substantially greater in an
algorithm that uses elliptic curves. In the protocol
presented in this paper, we use a slight modification
of the ECDSA scheme as discussed next.
The ECDSA key generation requires three domain
parameters, that are considered public domain infor-
mation, those parameters are the elliptic curve E, a
base point P of prime order n. With this informa-
tion the ECDSA key generation procedure generates
the public key Q and the private key d by computing
Q = dP. The digital signature of a given message m
consists of a pair (r, s).
Let k (the integer k is called the embedding degree
of the elliptic curve E) be the smallest positive inte-
ger such that n|(p
km
− 1). Then, there exists a unique
subgroup G
2
of order n defined in the multiplicative
214
López-García L., Rodríguez-Henríquez F. and A. León-Chávez M. (2008).
AN E-VOTING PROTOCOL BASED ON PAIRING BLIND SIGNATURES.
In Proceedings of the International Conference on Security and Cryptography, pages 214-217
DOI: 10.5220/0001925802140217
Copyright
c
SciTePress

group F
∗
p
km
. We can now define a bilinear pairing on
(G
1
, G
2
) as the mapping ˆe : G
1
× G
1
−→ G
2
satisfy-
ing the following properties:
1. Bilinearity: ∀ R, S, T ∈ G
1
ˆe(S+ R, T) = ˆe(S, T) · ˆe(R, T)
ˆe(S, R+ T) = ˆe(S, R) · ˆe(S, T)
2. Non-degeneracy: ˆe(P, P) 6= 1
3. Computability: ˆe can be efficiently computed.
2.1 Blind Signatures
Blind signatures are digital signatures with the prop-
erty that the message to be signed is hidden from
the Signer authority by means of a blind factor.
This property can be exploited to offer anonymity
in the electoral process to all the participants. The
RSA blind signature scheme introduced by Chaum in
(Chaum, 1983), allows to obtain a signed document
but at the same time it guarantees that the signer en-
tity will not be able to know the document that has
just signed. Across the years, several blind signature
schemes have been proposed. Some examples include
a DSA-based blind signature scheme proposedin (Ca-
menisch et al., 1994), an Elliptic Curve Cryptography
(ECC) based blind signature presented in (Jena et al.,
2007), among others.
In 2003, Boldyreva (Boldyreva, 2003) proposed a
blind signature scheme based on pairings. That sig-
nature is computed into three steps, two of them must
be performed by the requester and one by the signer
entity. The required operations are summarized in Al-
gorithm 1. The algorithm starts when the requester
hash the message m to be signed to a nonzero group
element M ∈ G
1
. Then, the requester blinds M, by
computing a scalar multiplication as,
ˆ
M = bM, where
b is a random blind factor generated by her. Then,
the requester sends
ˆ
M to the signer entity. The signer
entity signs the message by performing a scalar mul-
tiplication on
ˆ
M using its private key d. Thereafter,
it sends the blind signed document to the requester.
After receiving the blind signature, the requester re-
moves the blind factor, using, b
−1
ˆ
γ = b
−1
· b · γ = γ.
Taking advantage of the pairing bilinear properties,
that signature can be verified by checking whether,
ˆe(Q, H
1
(m)) = ˆe(dP, M) = ˆe(P, M)
d
= ˆe(P, γ),
holds.
3 PROTOCOL DATAFLOW
Our scheme requires three entities: one of them re-
sponsible for authenticating, another responsible of
receiving and validating the votes and the last one
specifically responsible of performing the vote tally.
In the rest of this paper, these three authorities will be
called Authentication Server (AS), Voting Server (VS)
and Counting Server (CS), respectively.
Algorithm 1: BlindSignature (Boldyreva, 2003)
Blind factor: b ∈ Z
n
M = H
1
(m) where H
1
: {0, 1}
∗
−→ G
1
\ O .
Blindness:
ˆ
M = bM
Signing:
ˆ
γ = d
ˆ
M
Unblindness: γ = b
−1
ˆ
γ
Verification: ˆe(Q, H
1
(m)) = ˆe(P, γ)
In Figure 1, the interaction among the voter and the
three servers is depicted. The most important ex-
changed object, is the electoral ballot that contains the
vote. In the initial authentication phase, the voter re-
quests a blank electoral ballot B from the AS. This
request will be granted only in the case that the AS
authenticates the voter. If everything works fine, the
voter will receive a blank ballot blind signed by the
AS. Once that this action is accomplished the voter
fills out the ballot and then sends it to the VS. This
is done in a second phase called Voting phase. It is
worth remarking that the ballot must be signed by
the voter but using a public/privatekey pair especially
generated for signing the ballot. Finally, in the third
phase called the Counting phase, all the receivedvotes
are counted by the CS so that the election result can
be obtained.
4 THE PROPOSED PROTOCOL
Notation
o {d
AS
, Q
AS
} AS’ public/private key pair.
o {d
V
, Q
V
}, Cert
V
V’ public/private key pair and
digital certificate.
o {d, Q} public/private key of the vote.
o k
1
, k
2
∈ Z
n
, where k
1
is a unique identifier cho-
sen by V, whereas k
2
denotes a unique identifier
chosen by the AS.
o t a time stamp.
Figure 1: Structure and functionality of the proposed
scheme.
AN E-VOTING PROTOCOL BASED ON PAIRING BLIND SIGNATURES
215

o xky denotes the values x and y concatenated.
o b ∈ Z
n
denotes a random blind factor.
o {m}
ENC
x
denotes the encryption function that uses
the secret key x applied to the message m.
o {m}
X
denotes the ECC signature of the message
m generated by the entity X
4.1 Authentication Phase
The voter randomly generates his/her secret key d and
session key k
1
and it must compute the public key
Q, that he/she will use to sign the electoral ballot in
the next phase. In order to guarantee full anonymity,
these values should be different than the voter’s pub-
lic/private key.
It is customary to use the coordinate x of the point
R for obtaining the first value of the ECDSA signa-
ture in (r, s). For convenience, in our scheme we use
the pair (R, s) as the vote’s signature. This simpli-
fies the introduction of the voter’s unique identifier in
the vote signature. This way, R and Q are public val-
ues that will be sent to the VS. These parameters are
blindly sent to the AS for its signature, so that there is
no possibility of associating the vote with the voter in
the following phases.
In order to request a valid blank ballot, the voter
sends to the AS, his/her digital certificate and blinded
messages, all of them signed with his/her private key
(as shown in the authentication phase of Table 1).
{Cert
V
,
ˆ
Q,
ˆ
R, {
ˆ
Qk
ˆ
Rkt}
d
V
}
After receiving this message, the AS attempts to au-
thenticate the voter. In case of positive identification,
the AS assigns a unique identifier k
2
to that voter. This
value will be kept in the registers of the AS.
Before proceeding to sign the blind messages, the
AS mix up to k
2
with
ˆ
R doing the scalar multiplication
k
2
ˆ
R to avoid duplicity of the signature. In order to
avoid forgery, the AS requires a link value to relate
both voter’s signatures.
This value should not be altered by the voter and at
the same time it cannot be generated by the AS since,
otherwise, the anonymity of the voter will not be pre-
served. These two restrictions suggest that a good
candidate for the link value could be a parameter that
can be taken from the vote’s signatures. k
2
ˆ
R satisfies
both restrictions, owed that it can not be modified by
the voter and neither the AS can link it with the voter.
Then, the AS adds k
2
ˆ
R to
ˆ
Q.
Finally, the AS signs the blind messages and
replies sending the parameter k
2
encrypted with
voter’s public key Q
V
along with the two blind signa-
tures. In order to guarantee its authenticity, the whole
Table 1: The scheme proposed.
Authentication phase
Voter AS
k
1
, d, b ∈ [1, n− 1]
Q = dP, R = k
1
P
ˆ
Q = bQ,
ˆ
R = bR
{Cert
V
,
ˆ
Q,
ˆ
R, {
ˆ
Qk
ˆ
Rkt}
d
V
}
−→
k
2
∈ [1, n− 1]
ˆ
γ
Q
= d
AS
(
ˆ
Q+ k
2
ˆ
R)
ˆ
γ
R
= d
AS
(k
2
ˆ
R)
{{k
2
kt}
ENC
Q
V
ˆ
γ
Q
,
ˆ
γ
R
, {
ˆ
γ
Q
k
ˆ
γ
R
kt}
d
AS
}
←−
γ
Q
= b
−1
ˆ
γ
1
γ
R
= b
−1
ˆ
γ
2
Voting phase
Voter VS
R = k
2
k
1
P
s = (k
2
k
1
)
−1
(vote+ R
x
d) mod n
{Q, R, s, vote, γ
Q
, γ
R
}
−→
ˆe(Q
AS
, Q+ R)? = ˆe(P, γ
Q
)
ˆe(Q
AS
, R)? = ˆe(P, γ
R
)
ECDSA VER(Q, R, s, vote)
Counting phase
CS VS
Compare ←− Valid Ballots
and counting
message is signed by the AS using its private key d
AS
.
{{k
2
kt}
ENC
Q
V
ˆ
γ
Q
,
ˆ
γ
R
, {
ˆ
γ
Q
k
ˆ
γ
R
kt}
d
AS
}
The voter receivesthe message, verifies that the signa-
ture comes from the AS and removes the blind factors.
After recovering his/her unique identifier k
2
, the voter
generates the signature for his/her vote with ECDSA
as shown in table 1 in the voting phase. The voting
ballot filled in by the voter is then sent to the VS as
{Q, R, s, vote, γ
Q
, γ
R
}
where (R, s) is the digital signature of vote, Q is the
public key of the signature (R, s), γ
Q
is a blind signa-
ture of Q and γ
R
is a blind signature of R.
The VS receives the ballot and verifies the blind
signatures. Let us recall that, the messages of blind
signatures γ
Q
and γ
R
are linked with R, then, VS ver-
ifies the signature γ
R
for R and γ
Q
for the message
Q+ R.
If the two signatures verify correctly, then the
VS proceeds to check the vote’s signature with the
ECDSA verification.
If the three signatures were all valid, the VS accepts
the ballot, produces a hash value of it and it stores the
SECRYPT 2008 - International Conference on Security and Cryptography
216
ballot. Finally, it sends to the voter the hash value of
its ballot as a receipt.
In the counting phase, the CS receives all the bal-
lots that were successfully validated by the VS. Since
each ballot contains three signatures, the only possi-
ble value that can be repeated is the one of the vote.
Therefore, in order to avoid duplicity, the CS com-
pares each received ballot with all the others already
stored. If two or more ballots have repeated signa-
tures, then they are candidates for possible fraud and
the CS will take as valid the first ballot.
5 ANALYSIS OF PROPOSED
SCHEME
Solution of possible Attacks to the System
- Associating the pair (vote, voter): Only the AS
has information that links the voter with the ballot
that was given to him/her. Nevertheless, if the AS
wants to obtain the voter information, it needs to
remove the blind factor b from the equation
ˆ
R =
bR. This equation is protected by the ECDLP and
therefore, it should be computationally unfeasible
to obtain it.
In order to identify any voter, it suffices that the
VS can manage to extract k
2
from k
2
P, since this
information leads to identify the voter from the AS
registers. However, three of the signatures con-
tained in the ballot, namely, γ
Q
, γ
R
and R are pro-
tected by the ECDLP.
- Modifying vote’s digital signatures: This attack
is prevented by the signature of the AS. The voter
must provethat the first part of the signatures were
signed by the AS during the authentication phase.
Otherwise, the ballot will not pass the checks per-
formed by the VS.
- Combining ballots by several voters: This attack
is prevented by the AS by including the link value
R to the blind message
ˆ
Q before signing them
(during the authentication phase). If a given voter
decides to combine his/her signatures with an-
other authorized voter, the link value will not be
the same for all the signatures. This will produce
that at least one of them will not verify.
Efficiency. The number of cryptographic algorithms
performed by our scheme in the authentication and
voting phases are summarized in Table 2.
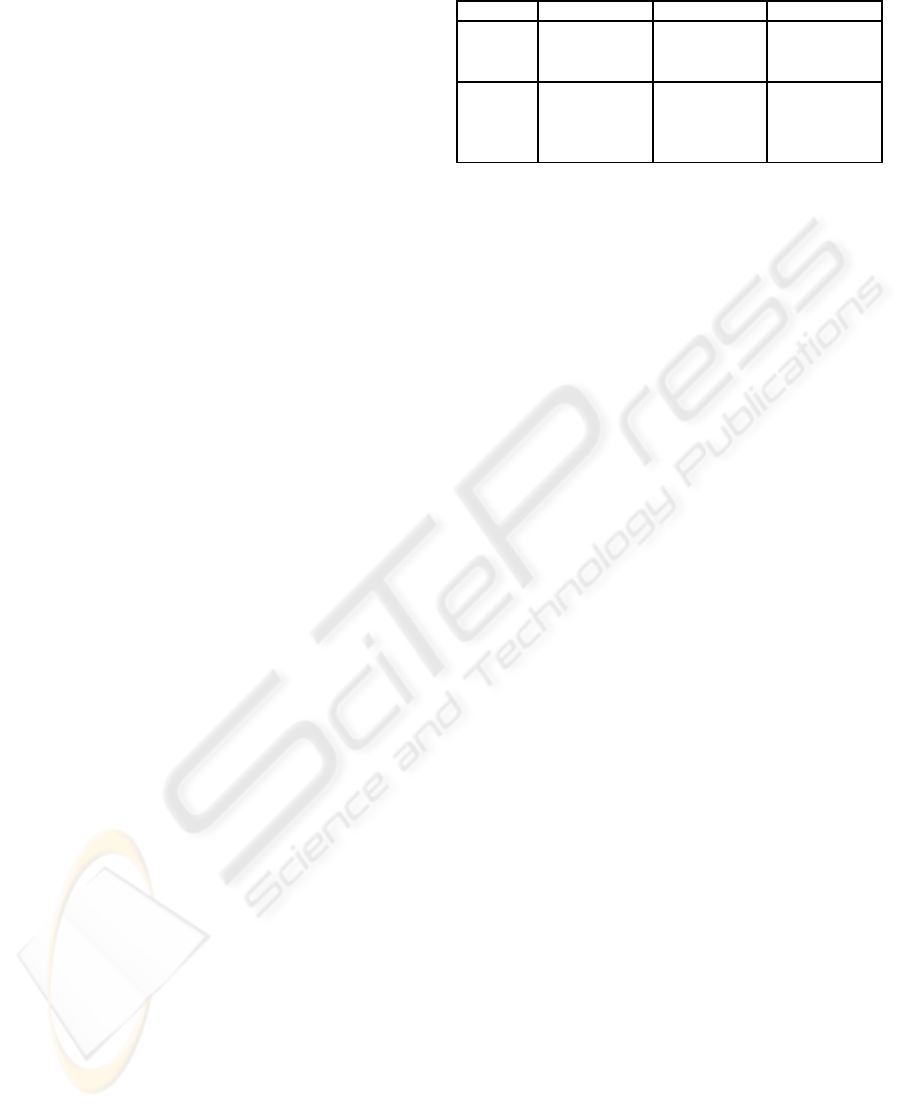
Table 2: Computational Cost of our Protocol by Phase.
Phase Voter AS VS
Auth. 6 scalar
mult.
2 scalar
mult.
-
1 inversion -
Voting 1 scalar
mult.
4 pairing
1 inversion 2 scalar
mult.
6 CONCLUSIONS
In this paper we presented an e-voting security pro-
tocol that utilizes pairing-based blind signatures and
ECDSA digital signatures as its main building blocks.
The pairing-based blind signatures help to bring bet-
ter security to the system guaranteing the anonymity
of the voters, whereas the ECDSA digital signatures
are used to assure votes’ integrity.
REFERENCES
Boldyreva, A. (2003). Threshold Signatures, Multisigna-
tures and Blind Signatures Based on the Gap-Diffie-
Hellman-Group Signature Scheme. In PKC ’03: Pro-
ceedings of the 6th International Workshop on Theory
and Practice in Public Key Cryptography, pages 31–
46. Springer-Verlag.
Camenisch, J., Piveteau, J. M., and Stadler, M. (1994).
Blind Signatures Based on the Discrete Logarithm
Problem. In Advances in Crypology - EUROCRYPT
’94, LNCS, 950:428–432.
Chaum, D. (1983). Blind Signatures for Untraceable Pay-
ments. Advances in Cryptology Proceedings of Crypto
’82, pages 199–203.
Jena, D., Kumar, S., and Majhi, B. (2007). A Novel
Untraceable Blind Signature Based on Elliptic Curve
Discrete Logarithm Problem. International Journal
of Computer Science and Network Security, IJCSNS,
7(6):269–275.
NIST (1994). Digital Signature Standard (DSS). Federal
Information Processing Standards Publications (FIPS
PUBS). http://www.itl.nist.gov/fipspubs/fip186.htm.
Qadah, G. and Taha, R. (2006). Electronic Voting Systems:
Requirements, Design and Implementation. Computer
& Interfaces, 29(3):376–386.
AN E-VOTING PROTOCOL BASED ON PAIRING BLIND SIGNATURES
217
