
A NEW PROBABILISTIC REKEYING METHOD FOR SECURE
DYNAMIC GROUPS
Shankar Joshi and Alwyn R. Pais
Department of Computer Engineering, National Institute of Technology Karnataka
Surathkal, Srinivasnagar, Mangalore - 574157, India
Keywords:
LKH optimization, key management, secure group communication.
Abstract:
Logical Key Hierarchy (LKH) is a basic method in secure multicast group rekeying. LKH maintains a balanced
tree which provide uniform cost of O(log N) for compromise recovery, where N is group size. However, it
does not distinguish the behavior of group members even though they have different probabilities of join or
leave. When members have diverse changing probability the gap between LKH and the optimal rekeying
algorithm will become bigger. The Probabilistic optimization of LKH (PLKH) scheme, optimized rekey cost
by organizing LKH tree with user rekey characteristic. In this paper, we concentrate on further reducing the
rekey cost by organizing LKH tree with respect to compromise probabilities of members using new join and
leave operations. Simulation results show that our scheme performs 18% to 29% better than PLKH and 32%
to 41% better than LKH.
1 INTRODUCTION
Multicast rekeying is one of the most visited areas in
network security. Many multicast based applications,
e.g., pay per view, online auction, multimedia confer-
encing, stock quote distribution, news dissemination
and networked gaming, require a secure communica-
tion model. The data in these applications need to be
secured from intruders as it is confidential or it has
monetary value.
However, IP Multicast, the multicast service pro-
posed for the Internet does not provide any secu-
rity mechanisms. Indeed, anyone can join a multi-
cast group to receive data from the data sources or
send data to the group. In other words, IP multicast
protocol does not support “closed” groups. There-
fore, cryptographic techniques have to be employed
to achieve data confidentiality.
One solution is to let all members in a group share
a key that is used for encrypting data. To provide
backward and forward confidentiality(D. M. Wallner
and Agee, 1999), this shared key has to be updated
on every membership change and redistributed to all
authorized members securely. This is referred to as
“group rekeying”.
A simple approach for rekeying a group is one in
which the group key server encrypts and sends the up-
dated group key individually to each member. This
approach is not scalable because its cost increases lin-
early with the group size. Hence, group rekey scala-
bility is a challenging issue for large groups having
frequent membership changes.
In recent years, many approaches for scal-
able group rekeying have been proposed such as
LKH(C. K. Wong and Lam, 2000)(D. M. Wallner
and Agee, 1999), OFT(McGrew and Sherman, 2003),
ELK(A. Perrig, 2001), SDR(D. Naor and Lotspiech,
2001) and SHKD(Donggang Liu and Sun, 2003).
Among these LKH and its variants are widely used
schemes. Further, many optimization techniques
are proposed for LKH. The schemes proposed in
(R. Canetti and Pinkas, 1999)(Bezawada and Kulka-
rni, 2004) optimize network bandwidth; the schemes
in (S. Setia, 2000)(Y. Yang and Lam, 2001) opti-
mize rekey cost on membership changes; finally the
schemes in (Sencun Zhu and Jajodia, 2003)(Onen and
Molva, 2004)(Xu and Sun, 2005)(Selc¸uk and Sidhu,
2000) restructure the LKH tree to optimize either
rekey cost, bandwidth used or processing time.
In this paper, we present a method for reducing
rekey cost in secure multicast groups by organizing
LKH tree with respect to member’s rekey probabil-
ities using our new join and leave operations. The
contributions of our paper are as follows:
• We present our insert and delete operations on
LKH tree which will reduce the cost of rekeying
325
Joshi S. and R. Pais A. (2008).
A NEW PROBABILISTIC REKEYING METHOD FOR SECURE DYNAMIC GROUPS.
In Proceedings of the International Conference on Security and Cryptography, pages 325-330
DOI: 10.5220/0001928703250330
Copyright
c
SciTePress

on member compromise/leave.
• We propose new key identifier assignment method
which generates unambiguous key identifiers for
nodes in the tree.
• We provide modified PUT operation which reduce
rekey cost on member join. Finally, we show that
our method reduces the rekey cost compared to
LKH and PLKH.
Organization of the Paper. The paper is organized
as follows. In Section 2, we describe various methods
available in literature to optimize LKH scheme. In
Section 3, we discuss various problems with PLKH.
In Section 4, we describe our scheme. In section 5,
we present the simulation results and analysis of the
results. Finally, in Section 6, we conclude our work.
2 RELATED WORK
There are many optimization schemes proposed in
literature for LKH. Some of them optimize network
bandwidth, some reduce rekeycost and others restruc-
ture LKH tree.
The OFC(R. Canetti and Pinkas, 1999) proposed
a variation of LKH which reduces the communication
overhead from LKH’s 2(log
2
N)– 1 to (log
2
N); but it
is limited to the binary key tree case. The Bezawada
scheme(Bezawada and Kulkarni, 2004) proposed a
key distribution algorithm for distributing keys to
only those users who need them. It proposes a com-
pact descendant tracking scheme to track the descen-
dants of the intermediate nodes in the multicast tree.
In the schemes (S. Setia, 2000)(Y. Yang and Lam,
2001), the groups are rekeyed periodically instead of
on every membership change which reduce both the
processing and communication overhead at the key
server.
The scheme in (Sencun Zhu and Jajodia, 2003),
proposed to partition the key tree using temporal pat-
terns of group members which reduce the overhead of
rekeying. The tree is partitioned into S–partition for
short duration members and L–partition for long du-
ration members. In (Onen and Molva, 2004) scheme,
the key server partitions members in different cate-
gories based on their membership duration.
In Refined LKH scheme(Xu and Sun, 2005), on
member join the member behavior namely active and
non–active is used to partition the member. On leave
by a member, “dirty path” is set in the path from
leaving node to root and rekeying is delayed until a
join operation in the same path of leaving member.
This scheme tries to merge leave operation rekey cost
with next join operation in that sub tree. But the per-
formance of algorithm is not adequate in all circum-
stances.
Probabilistic optimization of LKH (Selc¸uk and
Sidhu, 2000), called PLKH, show that it could be ben-
eficial to use an unbalanced key tree in some cases.
The idea in PLKH is to organize the key tree with re-
spect to the compromise probabilities of members, in
a spirit similar to data compression algorithms such
as Huffman and Shannon-Fano coding. Basically, the
key server places members who are is more likely to
be revoked closer to the root of the key tree. PLKH
ensures that the keys each member is holding after an
insert operation is same as those it was holding before
the insertion.
3 SHORTCOMINGS OF PLKH
Although the PLKH scheme reduces the rekeying
cost compared to LKH, it has some shortcomings
too. PLKH has three shortcomings which we are dis-
cussing below.
3.1 Strict Binary Tree Structure
On membership change, PLKH always ensures that
tree formed is strict binary tree. On member join,
PLKH balances the tree such that all the nodes will
have either two child or none. This increases the
depth of newly inserted member node which in turn
increases rekey cost. On deletion of a node, any node
with single child is also removed from tree. This ad-
versely affects the probability value of that deleted
node.
3.2 Probability Considered
PLKH considers cumulative probability i.e. X.p is
equal to the probability of the corresponding mem-
ber if X is a leaf node, and it is equal to X.left.p +
X.right.p, if X is an internal node. The insert oper-
ations proposed check this cumulative probability for
insert operation. This pushes new node down the tree,
even though new node may have higher rekey proba-
bility than some of the nodes on its path to tree root.
Another main problem with cumulative probabil-
ity is that it changes on every membership change
done in the subtree. On membership change, the key
held by nodes in the path from changed member node
to root are refreshed and their cumulative probability
field gets updated to reflect the membership changes.
SECRYPT 2008 - International Conference on Security and Cryptography
326
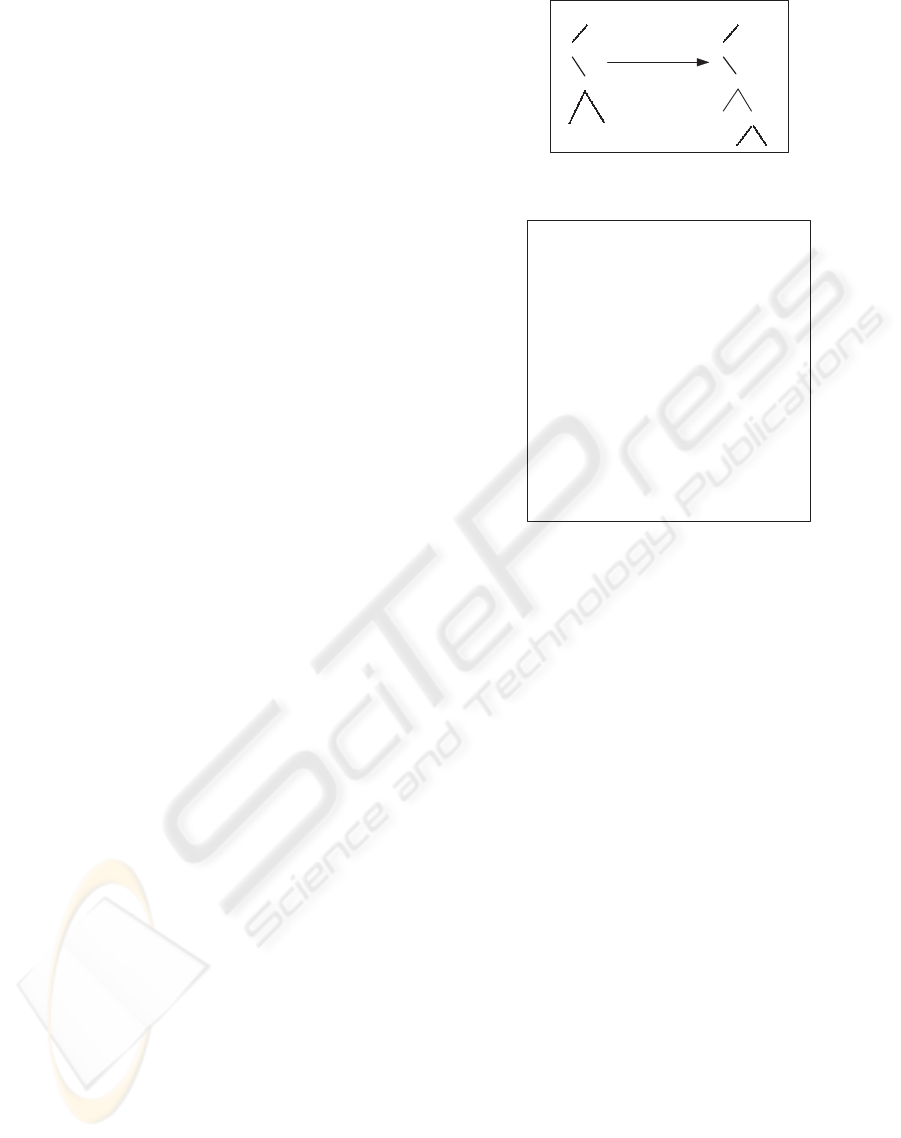
3.3 Ambiguous Key Identifiers
PLKH does not discuss how the key identifiers are
assigned. The key identifier generated using origi-
nal LKH identifier scheme or by using special flag
indicator for node created in PUT operation (Selc¸uk
and Sidhu, 2000) will end up in having some nodes
with ambiguous key identifiers. This problem arises
as PLKH does not affect existing nodes on member-
ship change; so when a change occurs only nodes in
the path from member node to root are updated. But
this information is not updated in descendants of af-
fected member node.
4 OUR SCHEME
In next sections, we describe our insert and delete op-
erations on LKH tree organized with respect to mem-
ber’s rekeying characteristic. We also describe our
new key identifier assignment scheme which gener-
ates unambiguous identifiers for nodes in the tree.
4.1 Node Types
We first define three types of nodes which are needed
by our scheme; namely physical, logical and replace-
able. A physical node is created when a member joins
the group. A physical node represents a member in
real world. A logical node is created when our modi-
fied PUT (MPUT) is executed. Our scheme deletes a
physical node only if it’s a leaf node; otherwise we set
it as replaceable node. A replaceable node represents
node which is not deleted from the tree due to depen-
dent nodes. A replaceable node will be replaced back
as physical node with suitable member information
on future join operations.
4.2 MPUT Operation
We define new PUT operation called Modified
PUT (MPUT). In MPUT, we create a logical node
whereas PUT operation of PLKH (Selc¸uk and Sidhu,
2000) creates normal(physical) intermediate node.
To insert new node N into tree using MPUT, new
logical node L is created at certain location in
tree such that N will be its left child and P will
be its right child (see Figure 1). GP, the previ-
ous parent of node P, will now point to node L.
The initial probability of a logical node is set to
max(leftChild.initprob, rightChild.init prob) + 1.
Root
GP
P
L
N
Root
GP
P
MPUT (N, P)
Figure 1: Our MPUT operation. It creates new logical node
L with P & N as its children.
insert(N, GP, P, direction)
if(P!=NULL){
if(P.initprob< N.initprob AND P!=TR){
if(P.type=replaceable)
replaceNode(P, N)
else if(isChildSlotFull(P)=False)
MPUT(N, P)
}
if(leftProb(P)>rightProb(P))
insert(N, P, P.right, right)
else
insert(N, P, P.left, left)
}
else{
if(direction = left)
insertNodeToLeft(GP, N)
else
insertNodeToRight(GP, N)
}
Figure 2: Our insert operation which considers the node’s
initial probability.
4.3 Insert Operation
Our insert operation inserts new node into suitable lo-
cation using one of the following functions MPUT,
insertNodeToLeft, insertNodeToRight and replaceN-
ode (see Figure 2). Here, instead of considering cu-
mulative probability which keeps on changing based
on join/leave in sub tree, we consider member’s rekey
probability called now onwards as initial probabil-
ity. Our insert algorithm takes no additional compu-
tational cost and has complexity of O(log d), where
d is depth of inserted member in the tree. If node’s
probability is greater than parent probability and node
is replaceable then we replace its details with new
member details and set it as physical node. This re-
duces possible PUT operation thus reducing mem-
ber’s depth by at least 1. The insertNodeToLeft and
insertNodeToRight are regular node insert operations
which insert new node at either left or right side of
given parent node. The isChildSlotFull returns True
if all the child slots are in use otherwise False. Con-
dition P 6= TR ensures that TreeRoot is not changed,
which represent group coordinator. Our insert algo-
rithm imitates Shannon-Fano Tree (Selc¸uk and Sidhu,
2000).
A NEW PROBABILISTIC REKEYING METHOD FOR SECURE DYNAMIC GROUPS
327
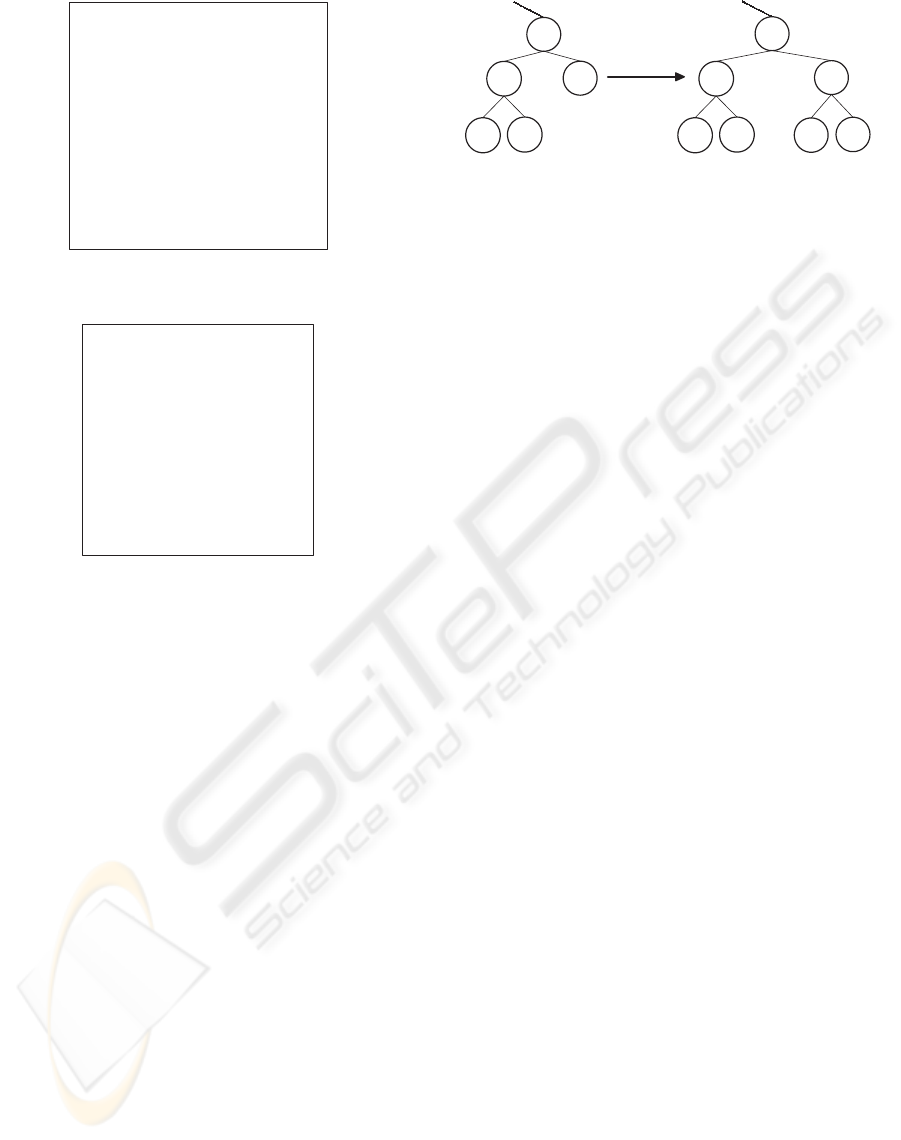
deleteNode(N)
P=getParent(N)
direction=getChildDirection(P, N)
if(isLeafNode(N)){
if(direction=Left)
deleteNodeFromLeft(P)
else
deleteNodeFromRight(P)
}
else{
if(N.type=physical)
setNodeAsReplacable(N)
}
if(isLeafNode(P) AND P.type !=physical)
deleteNode(P)
Figure 3: Our delete operation which removes non-physical
leaf nodes.
assignKeyID(P,C, direction)
keyid=P.keyid
if(direction=Left)
strcat keyid, “L”
else
strcat keyid, “R”
if C.type=logical
strcat keyid, ”x”
id=getFreeSlot(P, C.type)
strcat keyid, id
C.keyid=keyid
Figure 4: Our key identifier assignment algorithm.
4.4 Delete Operation
Our delete operation deletes a physical node only if
it’s a leaf node; otherwise we set its type as replace-
able and refresh affected keys (see Figure 3). On dele-
tion of specified node if its parent node becomes leaf
and is of logical or replaceable type, then we remove
the parent also as it doesn’t represent any real world
member and has no dependent.
4.5 Key Identifier Assignment
We provide a generic key identifier assignment
scheme which avoids ambiguous key identifier prob-
lem discussed earlier. On insertion of a new child C
whose parent is P, the assignment scheme will gener-
ate identifier as shown in Figure 4.
Here, getFreeSlot recursively searches until a non-
logical parent is found. It then returns index to a free
child slot. The ‘L’ and ‘R’ indicate the child direc-
tion with respect to its parent. This scheme ensures
that key identifiers are unambiguous. Note that we
add ‘x’ flag only for logical nodes. The ‘x’ flag helps
in direction correction to trace descendants.
MPUT(N, P)
GP
P
..R3
..R3L1
..R3L1L1
..R3L1R2
..R3R2
GP
L
..R3'
..R3L1
..R3L1L1 ..R3Rx1L3
..R3Rx1
N
P
..R3L1R2 ..R3R2
Figure 5: Example shows the working of our key identifier
assignment algorithm.
4.6 Tracing Node using Key Identifier
Tracing a node with our key identifier takes d steps,
where d is node’s depth. An example is given in Fig-
ure 5 for understanding. On MPUT(N, P), keys of all
the nodes from GP to root are refreshed. Here, the key
R3 is refreshed as R3
′
.
Note here that after MPUT operation if we need
to trace node P with key identifier ..R3R2, we first
move up to node L using direction indicators ‘L’ &
‘R’ representing left and right directions. At node L,
we detect that it’s logical. Now we do direction cor-
rection. At any stage when we get a logical node, if
the remaining part of node to be traced does not have
‘x’ flag indicator then we always move in right di-
rection irrespective of L or R of remaining part. This
is because the MPUT always inserts new node to left
and parent to right. The left sub tree will have nodes
with ‘x’ prefix in their remaining part. Since the P
node’s remaining part R2 does not have ‘x’ flag in-
dicator, so we move in right direction to find node at
next level.
4.7 Choosing Probability
To use the insertion algorithm as described above, it
is crucial to know the probability values of all mem-
bers in the tree at insertion time. This requirement
is not practical since computing the p
i
values would
require the knowledge of the rekey time probability
functions for all members in the tree. Moreover, even
if the rekey time probability functions are known for
all members, the p
i
values will change continuously
as members stay in the group. So, we use the weight
based scheme proposed in (Selc¸uk and Sidhu, 2000).
The weight assignment for the insertion algorithm
is the inverse of the mean inter-rekey time of mem-
bers; i.e.,
w
i
= 1/µ
i
(1)
where µ
i
is the average time between two rekeys by
member M
i
. There are two reasons for choice of 1/µ
i
as the weight measure among many other candidates:
SECRYPT 2008 - International Conference on Security and Cryptography
328

Static Group
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
128 256 512 768 1024
Number of users
Number of rekeys generated
LKH
PLKH
OPLKH
Figure 6: Simulation results for static group with various
group sizes.
1. Its simplicity and convenience.
2. In the special case where the members inter-rekey
time distributions are exponential, p
i
= w
i
/W gives
exactly the probability that M
i
will be the next
member to rekey.
5 SIMULATION RESULTS AND
ANALYSIS
We simulated LKH, PLKH and our method using the
ns2 network simulator (Simulator, 2008). We call our
scheme as OPLKH for simplicity. We performed ex-
periments on randomly generated network topologies
for groups of 128, 256, 512, 768 and 1024 members.
For each experiment, we selected a random set of
members join and leave the group and recorded num-
ber of rekey messages generated. We considered three
scenarios namely static, semi dynamic and dynamic
group.
5.1 Scenario 1 - Static Group
In this scenario, we assign relatively lesser rekey
probability to members. Most of the members in this
scenario stay in group till session is over. The mem-
bers are added at random intervals. In this scenario,
number of members to leave the group is chosen to
be roughly 25% of the group size. The members
leave the group at random times (chosen based on
their rekey probability) during the entire session of the
group. From the results got, we observe that for static
groups our scheme performs 41% better compared to
LKH and 29% better compared to PLKH (see Figure
6).
Semi-dynamic Group
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
128 256 512 768 1024
Number of users
Number of rekeys generated
LKH
PLKH
OPLKH
Figure 7: Simulation results for semi dynamic group with
various group sizes.
Dynamic Group
0
10000
20000
30000
40000
50000
60000
128 256 512 768 1024
Number of users
Number of rekeys generated
LKH
PLKH
OPLKH
Figure 8: Simulation results for dynamic group with various
group sizes.
5.2 Scenario 2 - Semi Dynamic Group
In this scenario, we assign relatively higher probabil-
ity to members compared to static group. Here also
the members are added at random intervals. In this
scenario, number of members to leave the group is
chosen to be roughly 50% of group size. The mem-
ber’s leave time is selected at random based on their
probabilities. From the results got, we observe that
for semi dynamic groups our scheme performs 38%
better compared to LKH and 21% better compared to
PLKH (see Figure 7).
5.3 Scenario 3 - Dynamic Group
In this scenario, we assign high probability to mem-
bers. The members are allowed to join and leave the
group at rapid rate. The group experiences lot of
join/leave operations in quick time which increases
the rekey messages generated. From the results got,
we observe that for dynamic groups our scheme per-
forms 32% better compared to LKH and 18% better
compared to PLKH (see Figure 8).
A NEW PROBABILISTIC REKEYING METHOD FOR SECURE DYNAMIC GROUPS
329

5.4 Analysis
The number of rekey messages generated for same
member join/leave operations in all scheme show that
our scheme, OPLKH, performs better than both LKH
and PLKH. OPLKH avoids strict binary tree struc-
ture, unwanted PUT operations and unnecessary logi-
cal nodes. The Table 1 shows rekey cost improvement
got by OPLKH over LKH & PLKH in different sce-
narios.
Table 1: Reduction in rekey cost of OPLKH compared to
LKH and PLKH.
over LKH (in %) over PLKH (in %)
Scenario 1 41 29
Scenario 2 38 21
Scenario 3 32 18
5.5 Limitations of Our Scheme
Some of the limitations of our scheme are discussed
here. Firstly, the key identifier assignment requires
more memory to store key identifiers. Typical LKH
scheme needs only 1 bit for choosing left or right
child. Whereas our scheme needs 6 bits with 1 bit
for direction, 1 bit for ‘x’ flag and 4 bits for index
to free child slot in parent. Second limitation is that,
though total nodes created are less than PLKH &
LKH schemes, our scheme treats some nodes harshly
in terms of depth assigned. Finally, our scheme only
ensures that tree structure is binary. It neither tries to
maintain strict binary tree as PLKH nor tries to bal-
ance all nodes at same level as LKH.
6 CONCLUSIONS
In this paper, we addressed the issue of reducing
rekey messages generated on member leave in se-
cure multicast groups. We presented new method to
form the LKH tree with member’s rekey characteris-
tics using our insert and delete operations. Also, we
gave generic key identifier assignment scheme which
avoids ambiguous key identifiers. The simulation re-
sults show that our scheme achieves rekey reduction
of 18% compared to PLKH and 32% on original LKH
for dynamic group of 1024 members.
REFERENCES
A. Perrig, D. Song, D. T. (2001). Elk, a new protocol for
efficient large group key distribution. In Proceedings
of the IEEE Security and Privacy Symposium 2001.
Bezawada, B. and Kulkarni, S. S. (2004). Distributing key
updates in secure dynamic groups. In International
Conference on Distributed Computing and Internet
Technology, ICDCIT 04.
C. K. Wong, M. G. and Lam, S. S. (2000). Secure group
communications using key graphs. In IEEE/ACM
Trans. Networking.
D. M. Wallner, E. J. H. and Agee, R. C. (1999). Key man-
agement for multicast: Issues and architectures. In
RFC 2627.
D. Naor, M. N. and Lotspiech, J. (2001). Revocation and
tracing schemes for stateless receivers. In Advances
in Cryptology -CRYPTO 2001, Springer-Verlag Inc.
LNCS 2139.
Donggang Liu, P. N. and Sun, K. (2003). Efficient self-
healing group key distribution with revocation capa-
bility. In Proceedings of the 10
th
ACM conference on
Computer and Communications Security.
McGrew, D. A. and Sherman, A. T. (2003). Key establish-
ment in large dynamic groups using one-way function
trees. In IEEE Transactions on Software Engineering.
Onen, M. and Molva, R. (2004). Group rekeying with a
customer perspective. In Proceedings of Tenth Inter-
national Conference on Parallel and Distributed Sys-
tems.
R. Canetti, J. Garay, G. I. D. M. M. N. and Pinkas, B.
(1999). Multicast security: A taxonomy and some ef-
ficient constructions. In Proc. IEEE INFOCOM ’99.
S. Setia, S. Koussih, S. J. (2000). Kronos: A scalable group
re-keying approach for secure multicast. In IEEE
Symp. on Security and Privacy.
Selc¸uk, A. A. and Sidhu, D. P. (2000). Probabilistic meth-
ods in multicast key management. In Proceedings of
the Third International Workshop on Information Se-
curity.
Sencun Zhu, S. S. and Jajodia, S. (2003). Performance opti-
mizations for group key management schemes for se-
cure multicast. In Proceedings of 23
rd
International
Conference on Distributed Computing Systems.
Simulator (2008). ns-2, vesion 2.32. In
http://www.isi.edu/nsnam/ns/.
Xu, Y. and Sun, Y. (2005). A new group rekeying method
in secure multicast. In International conference on
Computational intelligence and security.
Y. Yang, X. Li, X. Z. and Lam, S. (2001). Reliable group
rekeying: Design and performance analysis. In Proc.
of ACM SIGCOMM 2001.
SECRYPT 2008 - International Conference on Security and Cryptography
330
