FAR-END CROSSTALK IN ITERATIVELY DETECTED

MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEMS

Andreas Ahrens

Hochschule Wismar, University of Technology, Business and Design

Department of Electrical Engineering and Computer Science, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany

Christoph Lange

T-Systems Enterprise Services GmbH, Goslarer Ufer 35, 10589 Berlin, Germany

Keywords:

Twisted-pair Cable, OFDM, Singular-Value Decomposition, Multiple Input Multiple Output System, Iterative

Decoding, EXIT Charts.

Abstract:

Crosstalk between neighbouring wire pairs in multi-pair copper cables is an important disturbance, which

essentially limits the transmission quality and the throughput of such cables. For high-rate transmission, often

the strong near-end crosstalk (NEXT) disturbance is avoided or suppressed and only the far-end crosstalk

(FEXT) remains as crosstalk inﬂuence. In this contribution the effect of far-end crosstalk (FEXT) in iteratively

detected MIMO-OFDM transmission schemes is studied. EXIT (extrinsic information transfer) charts are used

for analyzing and optimizing the convergence behaviour of the iterative demapping and decoding.

1 INTRODUCTION

The local cable network substantially ensures the

ﬁxed subscriber access to telephone and data ser-

vices. For the most parts this ﬁxed access network

consists of multi-pair symmetric copper cables, where

based on electromagnetic coupling, electrical energy

passes over from one wire pair to adjacent ones and

crosstalk arises, if the signals in the distinct wire

pairs lie in the same or at least in overlapping fre-

quency ranges (Valenti, 2002). Crosstalk as an elec-

tromagnetic coupling between adjacent wire pairs is

one of the most limiting disturbances in local ca-

ble networks. Thereby near-end crosstalk (NEXT)

and far-end crosstalk (FEXT) occur in bidirectional

driven cables (Valenti, 2002). Since the NEXT is a

very strong disturbance (Valenti, 2002) several tech-

niques have been developed in order to avoid or sup-

press NEXT (Honig et al., 1990). In this case only

the FEXT remains as a crosstalk inﬂuence. Often

short cables are used in high-data rate systems in ﬁxed

access networks, e.g., optical ﬁbre transmission is

used up to a street cabinet or a building and the last

drop is bridged by copper cables. Interestingly, in-

vestigations in (Lange and Ahrens, 2005) have shown

that the FEXT impact is much stronger in short ca-

bles than in longer ones. Considering cables or ca-

ble binders as MIMO (multiple input multiple out-

put) channels, FEXT in multi-pair copper cables can

be seen as a possible application for MIMO tech-

niques. From broadband radio transmission channels,

it is well-known that MIMO techniques are able to

overcome the limiting factor of multipath propaga-

tion known from single-carrier transmission schemes

(Raleigh and Ciofﬁ, 1998; Raleigh and Jones, 1999).

Powerful coding algorithms are used in wireline

transmission systems. As an example it should be

mentioned, that in both voiceband modem technol-

ogy as well as in the latest VDSL2 (very-high rate

digital subscriber line) systems (ITU-T Recommen-

dation G.993.2, 2006), trellis-coded modulation is

used. Against this background, the novel contribu-

tion of this paper is that we illustrate the effect of

FEXT in iteratively detected MIMO-OFDM trans-

mission schemes, whereby both the uncoded as well

as the coded systems are restricted to support the same

user data rate within the same bandwidth. The per-

formance investigations are carried out by computer

simulations and conﬁrmed by EXIT (extrinsic infor-

mation transfer) charts (Brink, 2001).

The remainder of this paper is organized as fol-

lows: Section 2 introduces the cable characteristics

and in 3 the FEXT impact is analyzed. In 4 the

multicarrier MIMO system model is introduced and

Ahrens A. and Lange C. (2008).

FAR-END CROSSTALK IN ITERATIVELY DETECTED MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEMS.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 39-46

DOI: 10.5220/0001931300390046

 SciTePress

the performance metrics are given. The channel en-

coded MIMO system is introduced in section 5, while

the computation of the EXIT transfer function is pre-

sented in section 6. The associated performance re-

sults are presented and interpreted in Section 7. Fi-

nally, section 8 provides our concluding remarks.

2 CABLE CHARACTERISTICS

The distorting inﬂuence of the cable on the wanted

signal is modelled by the cable transfer function

( f) = e

−l

, (1)

where l denotes the cable length (in km) and

represents the characteristic cable frequency (in

MHz·km

) (Kreß and Krieghoff, 1973).

The far-end crosstalk coupling is covered by the

transfer function G

( f) with

( f)|

= K

·l · f

, (2)

whereby K

is a coupling constant of the far-end

crosstalk, which depends on the cable properties such

as the type of isolation, the number of wire pairs and

the kind of combination of the wire pairs within the

binders (Valenti, 2002; Galli and Kerpez, 2002a; Galli

and Kerpez, 2002b).

If the far-end crosstalk from several neighbouring

wire pairs is considered, with increasing distance of

the disturbing wire pair from the considered pair in a

cable the impact of far-end crosstalk decreases. Con-

sidering n

FEXT-disturbing wire pairs, in conformity

with cable measurements, this behaviour can be mod-

elled by (Valenti, 2002)

= n

0.6

·K

, (3)

where K

is the FEXT coupling constant for one dis-

turbing wire pair. By (3) it is taken into account, that

the wire pairs, which are located farther away from

the considered wire pair contribute less to the FEXT

disturbance than the wire pairs, which are located

closer to the considered wire pair (Kalet and Shamai

(Shitz), 1990; Valenti, 2002).

3 FEXT IMPACT

Since in the copper access network on the one hand

very short copper cables are used (e. g. in ﬁbre to

the cabinet or ﬁbre to the building architectures) and

on the other hand also longer copper cables are ap-

plied (e.g. in rural areas) it is of interest, how the

far-end crosstalk depends on the cable length (Lange

and Ahrens, 2005). Therefore at this point the length-

dependency of the FEXT is investigated in an exem-

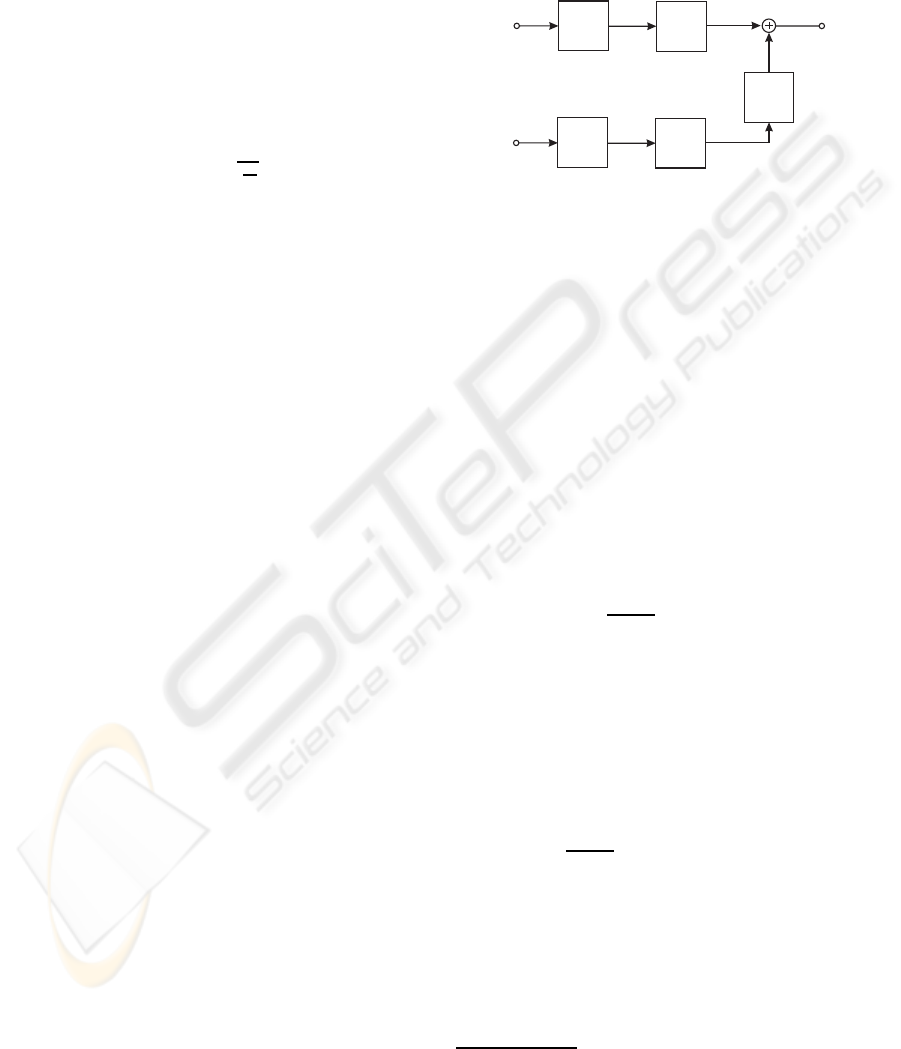
plary system according to Fig. 1. For simplicity of

calculations, this length dependency of the FEXT is

investigated by means of a baseband system.

q 1

(t)

q 2

(t)

(f)

s 1

(t)

s 2

(t)

(f)

k 1

(t)

k 11

(t)

k 21

(t)

Figure 1: Model of transmitter and cable with FEXT (ex-

ample: n = 2).

It is assumed, that each wire pair within the cable

is feeded by a system with identical mean properties

with respect to transmit ﬁltering, pulse frequency (or

symbol rate) f

= 1/T

, the number s of signalling

levels and the mean transmit power P

. The source

signals u

(t) and u

(t) traverse the transmit ﬁlters

with the transfer function G

( f). Then the wanted

transmit signal u

(t) passes the cable and causes the

signal u

k11

(t) with power P

k11

at the cable output,

whereas the FEXT signal u

k21

(t) (with power P

k21

)

originates at the cable output, after the transmit signal

(t) in the neighbouring wire pair passed through

both, the FEXT coupling and the cable transfer func-

tion (Fig. 1). The power

k11

= U

−1

+∞

−∞

( f) ·G

( f)|

df (4)

of the wanted signal u

k11

(t) at the cable output de-

creases monotonically with rising cable length, since

with increasing cable length the lowpass effect of the

cable G

( f) becomes stronger and hence the area be-

low |G

( f)·G

( f)|

decreases. From a practical point

of view the power

k21

−1

+∞

−∞

( f)·G

( f)|

df (5)

of the FEXT signal u

k21

(t) at the cable output (n

= 1)

is an interesting indicator for the strength of the FEXT

disturbance. In general, this FEXT power depends on

the frequency (i. e. signal bandwidth) and on the cable

length, because G

( f) and G

( f) are functions of the

frequency f and of the cable length l. Figure 2 shows

In this contribution a power with the dimension

(voltage)

(in V

) is used. At a real, constant resistor this

value is proportional to the physical power (in W).

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

0 0.2 0.4 0.6 0.8 1

−80

−70

−60

−50

−40

−30

= 10 MHz

= 40 MHz

= 100 MHz

l(in k m) →

10 ·lg(P

k 21

) (indB) →

Figure 2: FEXT power P

k21

at the cable output as a function

of the cable length l (parameter: f

the mean FEXT power (5) at the cable output de-

pending on the cable length l with root-raised cosine

transmit ﬁltering (roll-off factor r = 0.5) (Proakis,

2000) and the exemplary parameters P

= 1V

, s = 2

and K

= 2.6248 ·10

−17

(Hz

·km)

−1

for different

bit rates f

= f

·log

(s). At a ﬁxed bit rate (ﬁxed

required bandwidth) the FEXT power P

k21

only de-

pends on the cable length l. At very small cable

lengths ﬁrstly the FEXT power increases, since the

FEXT coupling according to (2) rises with increas-

ing cable length l. A maximum in the FEXT power

arises at relatively low cable lengths (below 0.2km),

because the FEXT power according to (5) via G

( f)

rises with increasing l and over G

( f) it decreases

with increasing cable length l, i.e., there is a depen-

dency of the FEXT power (5) on the cable length

in a opposite direction. At high symbol rates the

transmit spectrum is getting broader and this causes

a higher maximum in the FEXT power compared to

lower pulse frequencies (smaller bandwidth), because

the FEXT coupling (2) rises with frequency. The ca-

ble length, at which the maximum occurs, decreases

with increasing bit rate (increasing bandwidth of the

signal), because the lowpass impact of the cable takes

already a higher effect on a shorter cable.

In order to assess the effect of far-end crosstalk

on the wanted signal not only the pure FEXT signal

power is of interest, but rather the behaviour of the

powers of the wanted signal and the FEXT signal to

each other. This behaviour may be investigated by a

signal-to-FEXT-interference ratio (SFIR)

+∞

−∞

( f) ·G

( f)|

+∞

−∞

( f) ·G

( f)|

(6)

with modiﬁed FEXT coupling constants K

according

0 0.2 0.4 0.6 0.8 1

= 1

= 9

= 49

l(in k m) →

10 ·lg(ρ

) (indB) →

Figure 3: Signal-to-FEXT-interference ratio ρ

as a func-

tion of the cable length l (parameter: n

to the number n

of disturbing wire pairs in G

( f)

described in (3). Figure 3 shows the SFIR ρ

as a

function of the cable length at a ﬁxed bit rate of f

100MHz (and P

= 1V

, s = 2) for different numbers

= n−1 of disturbing wire pairs. With increasing

number n

of disturbers the FEXT power increases

and therefore the SFIR decreases. Since the FEXT

power (5) has a local maximum and the wanted signal

power (4) decreases monotonically with respect to the

cable length l, a minimum occurs in the SFIR function

according to (6).

In particular for short cables the FEXT impact

is very signiﬁcant. Therefore especially in the case,

where short copper cables are used the exploitation of

FEXT may be useful in order to improve the trans-

mission quality.

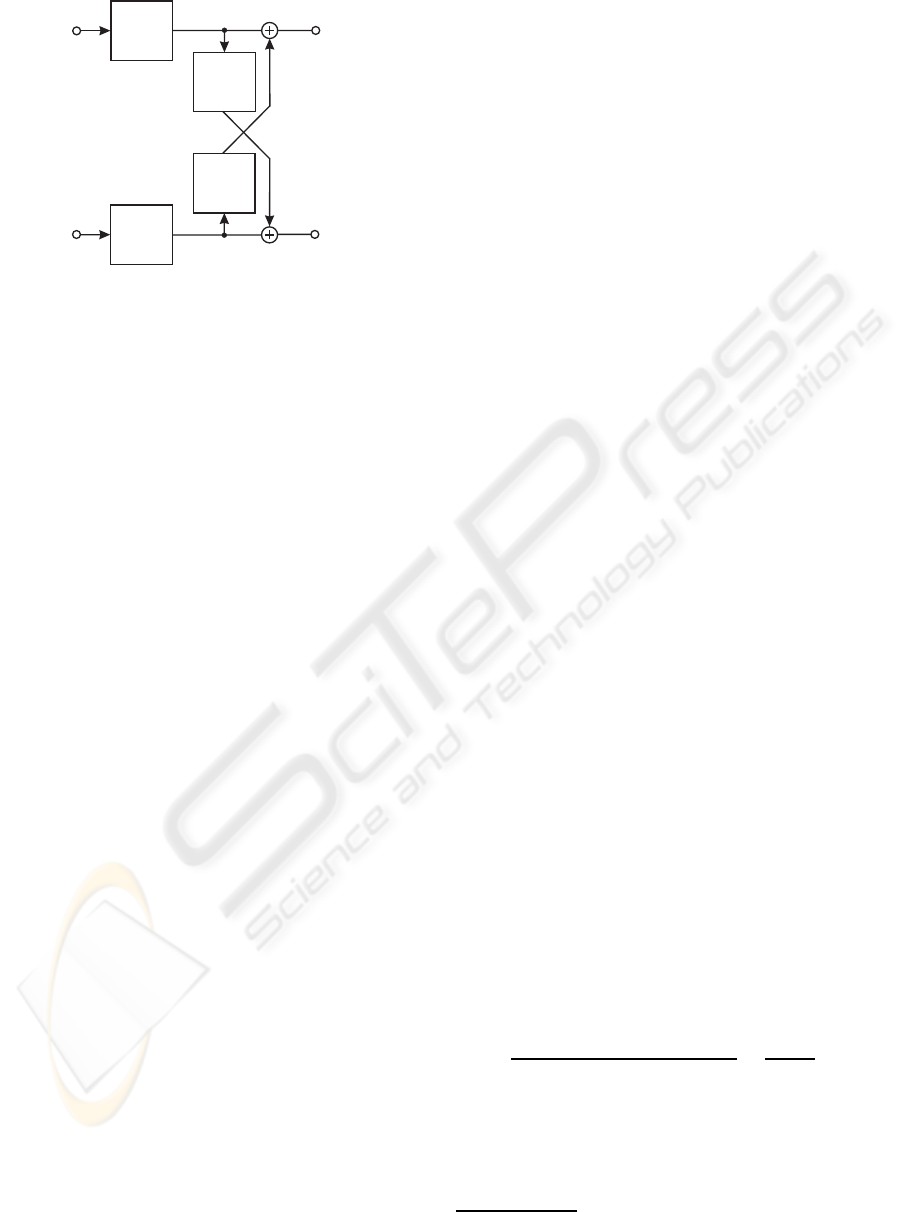
4 MIMO-OFDM SYSTEM MODEL

Now a whole cable binder is considered as a transmis-

sion channel with multiple inputs and multiple out-

puts (MIMO). The considered cable binder consists

of n wire pairs and therefore a (n, n) MIMO transmis-

sion system arises. The mapping of the transmit sig-

nals u

sµ

(t) onto the received signals u

kµ

(t) (with µ =

1,..., n) can be described accordingly to Fig. 4. On

each wire pair of the cable binder OFDM (orthogonal

frequency division multiplexing) is used as transmis-

sion technique to combat the effects of the frequency-

selective channel (Bahai and Saltzberg, 1999; Bing-

ham, 2000). In such a (n,n)-MIMO-OFDM system,

an N-point IFFT (N subchannels) modulated data sig-

nal is transmitted on every wire pair. The system is

modelled by

u = R·c+ w . (7)

FAR-END CROSSTALK IN ITERATIVELY DETECTED MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEMS

s 1

(t)

s 2

(t)

k 1

(t)

k 2

(t)

(f)

Figure 4: MIMO cable transmission model system with

FEXT (n = 2).

In (7), c is the (L×1) transmitted signal vector con-

taining the L = N n complex input symbols transmit-

ted over all n wire pairs. Using OFDM with a suf-

ﬁcient guard interval length, only symbols that are

transmitted over the same subcarrier can interfere

each other. The data vector c can be decomposed ac-

cording to

c =



,. ..,c



, (8)

where the (n ×1) vector c

contains the complex in-

put symbols transmitted over the κth subcarrier on

each wire pair. Furthermore u describes the (L ×1)

received vector and w is the (L×1) vector of the Ad-

ditive, White Gaussian Noise (AWGN) having a vari-

ance of U

for both the real and imaginary parts. Ap-

plying OFDM with a sufﬁcient guard interval length,

the matrix R in (7) gets a block diagonal structure ac-

cording to

R =







0 ··· 0

0 R

0 0 ··· R







. (9)

In equation (9) zero-matrices are denoted by 0 and

for the matrices R

(with κ = 1, ... ,N) the following

syntax is used







(κ)

··· r

(κ)

··· r

(κ)







, (10)

with the elements describing the couplings of the

data symbols on the subchannel κ. Based on the

symmetry of the considered transmission system r

(κ)

νµ

(for ν = µ) can be determined taking the FFT of

(t) = F

−1

( f)} into account. The elements

(κ)

νµ

(for ν 6= µ) consider the coupling between neigh-

bouring wire pairs and can be ascertained calculat-

ing the FFT of g

kfn

(t) = F

−1

( f) ·G

( f)}. The

κth value of this vector represents r

(κ)

νµ

. The ele-

ments r

(κ)

νµ

(for ν 6= µ) are assumed to be identical

for each κ, although in practical systems the cou-

pling between the wire pairs is slightly different and

it depends on their arrangement in the binder (Valenti,

2002). The subcarrier-speciﬁc interferences intro-

duced by the non-diagonal matrix R

require appro-

priate signal processing strategies. A popular tech-

nique is based on the SVD of the matrix R

, which

can be written as R

= S

·V

·D

, where S

and D

are unitary matrices and V

is a real-valued diagonal

matrix of the positive square roots of the eigenvalues

of the matrix R

sorted in descending order

. Us-

ing D

as preprocessing matrix at the transmitter and

as postprocessing matrix at the receiver side, the

overall transmission relationship results in

= S

·D

·c

+ w

) = V

·c

+ ˜w

. (11)

Here, the (n×n) matrix R

is transformed into n inde-

pendent, non-interfering layers having unequal gains.

Arranging the subcarrier speciﬁc received vectors y

according to (8), leads to the following description of

the transmission system according to

y = V·c+ ˜w. (12)

Therein the (L × L) matrix V has a block-diagonal

structure according to

V =







0 ··· 0

0 V

0 0 ··· V







. (13)

Based on the diagonal structure of the subcarrier spe-

ciﬁc (n×n) matrices V

, the channel matrix R is de-

composed into L = N n independent, non-interfering

layers having unequal gains.

In general, the quality of data transmission can be

informally assessed by using the signal-to-noise ratio

(SNR) at the detector’s input deﬁned by the half ver-

tical eye opening and the noise power per quadrature

component according to

ρ =

(Half vertical eye opening)

Noise Power

)

, (14)

which is often used as a quality parameter (Ahrens

and Lange, 2006). The relationship between the

signal-to-noise ratio ρ = U

and the bit-error

probability evaluated for AWGN channels and M-ary

The transpose and conjugate transpose (Hermitian) of

are denoted by D

and D

, respectively.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

Quadrature Amplitude Modulation (QAM) is given

by (Kalet, 1987; Proakis, 2000)

BER

log

(M)



1−

√



erfc





. (15)

When applying the proposed system structure, the

SVD-based equalization leads to different eye open-

ings per layer ℓ according to

(ℓ)

ℓ

·U

sℓ

, (16)

where U

sℓ

denotes the half-level transmit ampli-

tude assuming M

ℓ

-ary QAM and

ℓ

represents

the weighting factor (singular value) resulting from

the subcarrier-based equalization. Together with the

noise power per quadrature component, the SNR per

layer becomes

(ℓ)



(ℓ)



= ξ

ℓ

sℓ

)

. (17)

The bit-error probability per layer ℓ is given by

(Ahrens and Lange, 2006)

(ℓ)

BER



1−

√

ℓ



log

ℓ

)

erfc

ℓ

sℓ

. (18)

The resulting average bit-error probability assuming

different QAM constellation sizes results in

BER

∑

ν=1

log

)

∑

ℓ=1

log

ℓ

(ℓ)

BER

. (19)

Therein the number of transmitted bits per data block

results in

R =

∑

ℓ=1

log

ℓ

, (20)

assuming that all L layers are used for the data trans-

mission. Considering QAM constellations, the aver-

age transmit power P

sℓ

per layer ℓ may be expressed

as (Forney et al., 1984; Kalet, 1989)

sℓ

ℓ

−1) . (21)

Combining (17) and (21), the layer-speciﬁc SNR re-

sults in

(ℓ)

= ξ

ℓ

2(M

ℓ

−1)

sℓ

. (22)

Using a parallel transmission over N subchannels the

overall mean transmit power per wire yields to

= N ·P

sℓ

= N

sℓ

ℓ

−1) , (23)

and results in a total transmit power of nP

by taking

n wire-pairs into account. Assuming that the transmit

i b

1,k

2,k

L,k

encoder

∏

Mapper

1,k

2,k

L,k

MUX and Buffer

Figure 5: The channel-encoded MIMO-OFDM transmitter

structure.

power is uniformly distributed over the number of ac-

tivated layers per wire, i. e., P

sℓ

= P

/N, the half-level

transmit amplitude U

sℓ

per layer results in

sℓ

2N(M

ℓ

−1)

. (24)

The signal-to-noise ratio per layer ℓ, deﬁned in (17),

results together with (24) in

(ℓ)

= ξ

ℓ

2N(M

ℓ

−1)

. (25)

5 CODED MIMO-OFDM SYSTEM

The transmitter structure including channel coding is

depicted in Fig. 5. The encoder employs a rate 1/4

non-recursive, non-systematic convolutional (NSC)

code using the generator polynomials(7,7,7,5) in oc-

tal notation. The uncoded information is organized

in blocks of N

bits, consisting of at least 1000 bits,

depending on the speciﬁc QAM constellation used.

Each data block i is encoded and results in the block

b consisting of N

= 2N

+ 8 encoded bits, includ-

ing 2 termination bits. The encoded bits are inter-

leaved using a random interleaver and stored in the

vector

b. The encoded and interleaved bits are then

mapped onto the layers. The task of the multiplexer

and buffer block of Fig. 5 is to divide the vector of

encoded and interleaved information bits

b into sub-

vectors (

1,k

2,k

,··· ,

L,k

), each consisting of R bits

according to the chosen throughput. The individual

binary data vectors

ℓ,k

are then mapped to the QAM

symbols c

ℓ,k

according to the speciﬁc mapper used.

The iterative demodulatorstructure is shown in Fig. 6.

When using the iteration index ν, the ﬁrst iteration of

ν = 1 commences with the soft-demapper delivering

the N

log-likelihood ratios (LLRs) L

(ν=1)

(

b) of the

encoded and interleaved information bits, whose de-

interleaved version L

(ν=1)

a,1

(b) represents the input of

the convolutional decoder as depicted in Fig. 6. This

channel decoder provides the estimates of the origi-

nal uncoded information bits, i. e. L

(ν=1)

(i), as well

FAR-END CROSSTALK IN ITERATIVELY DETECTED MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEMS

1,k

2,k

L,k

Soft Demapper

(ν)

(

∏

−1

∏

(ν)

a,1

(b)

decoder

(ν)

(i)

(ν)

(b)

(ν−1)

e,1

(b)

(ν)

a,2

(

Figure 6: Iterative demodulator structure.

as the LLRs of the N

NSC-encoded bits in the form

(ν=1)

(b) = L

(ν=1)

a,1

(b) + L

(ν=1)

e,1

(b) . (26)

As seen in Fig. 6 and Eq. (26), the LLRs of the

NSC-encoded bits consist of the receiver’s input sig-

nal itself plus the extrinsic information L

(ν=1)

e,1

(b),

which is generated by subtracting L

(ν=1)

a,1

(b) from

(ν=1)

(b). The appropriately ordered, i. e. interleaved

extrinsic LLRs are fed back as a priori information

(ν=2)

a,2

(

b) to the soft demapper of Fig. 6 for the sec-

ond iteration. The N

LLRs L

(ν)

(

b) are composed of

the subvectors (L

(ν)

(

1,k

),L

(ν)

(

2,k

),··· , L

(ν)

(

L,k

)),

each consisting of R elements according to the cho-

sen throughput. Each vector L

(ν)

(

ℓ,k

) is generated

by the soft demapper from the MIMO channel’s out-

put y

ℓ,k

and the a-priori information L

(ν)

a,2

(

ℓ,k

) pro-

vided by the channel decoder. After the ﬁrst iteration,

this a-priori information emerges from the N

LLRs

(ν)

a,2

(

b), which are again decomposed into the subvec-

tors (L

(ν)

a,2

(

1,k

),L

(ν)

a,2

(

2,k

),··· ,L

(ν)

a,2

(

L,k

)), each con-

sisting of R elements.

6 EXIT CHART

The transmitted data sequence B is multiplexed onto

the different used layers ℓ and results in the layer spe-

ciﬁc sequence

ℓ

with ℓ = 1, 2, ...,L. The stationary

binary input sequence B

ℓ

= [B

ℓ,1

ℓ,2

,. ..,B

ℓ,k

,. ..]

consists of r.v.s B

ℓ,k

, where the corresponding real-

izations b

ℓ,k

have an index length of 1 bit and are

taken from a ﬁnite alphabet B = {0,1} The map-

per output sequence C

ℓ

= [C

ℓ,1

ℓ,2

,. ..,C

ℓ,k

,. ..] on

the ℓ-th layer consists of r.v.s C

ℓ,k

, where the cor-

responding realizations c

ℓ,k

have an index length of

Random variables (r.v.s) are denoted with capital letters

and their corresponding realizations with lower case letters.

Sequences of random variables and realizations are indi-

cated by boldface italics letters (as B or b ). Furthermore,

boldface roman letters denote vectors (as B or b). The time

instant is denoted with k and the layer with ℓ.

log

ℓ

) bits and are taken from a ﬁnite alphabet

C = {0, 1,.. .,M

ℓ

−1}. The symbols c

ℓ,k

are trans-

mitted over independent channels resulting in the re-

ceived values y

ℓ,k

. The resulting layer-speciﬁc model

is shown in Fig. 7. The a priori channel models the

a priori information used at the soft demapper. The

sequence A

ℓ

= [A

ℓ,1

ℓ,2

,. ..,A

ℓ,k

,. ..] with the cor-

responding realizations a

ℓ,k

contains the a priori LLR

information passed to the demapper.

ℓ,k

Mapper

Comm.

channel

A Priori

channel

Soft Demapper

Figure 7: Transmission model analyzing the ℓ-th layer.

EXIT charts visualize the input/ output character-

istics of the soft demapper and the decoder in terms

of a mutual information transfer between the data se-

quence B

ℓ

and the sequence A

ℓ

of the a priori LLR

information at the input of the soft demapper, as well

as between B

ℓ

and the sequence E

ℓ

of the extrinsic

LLR at the output, respectively. Denoting the mu-

tual information between two r.v.s X and Y as I(X;Y)

we may deﬁne for a given sequence B

ℓ

the quantities

ℓ,A

= I(A

ℓ

) as well as I

ℓ,E

= I(E

ℓ

). Herein,

ℓ,A

represents the average a priori information and

ℓ,E

the average extrinsic information, respectively

(Ahrens et al., 2008). The transfer characteristic T of

the soft demapper is given by I

ℓ,E

= T(I

ℓ,A

,ρ), where

ρ represents the SNR of the communication channel.

Analyzing the outer decoder in a serially concatenated

scheme T does not depend on ρ. An EXIT chart is

now obtained by plotting the transfer characteristics T

for both the demapper and the decoder within a single

diagram, where the axes have to be swapped for one

of the constituent decoders (Brink, 2001) (normally

the outer one for serial concatenation).

Transmitting R bits per data block, a layer speciﬁc

parameter α

(ℓ)

can be deﬁned as follows

(ℓ)

log

ℓ

, (27)

describing the fraction of the data sequence B that is

transmitted over the ℓth layer, i. e. B

ℓ

. The mutual

information for a given sequence B and the extrinsic

LLR E at the output is obtained by

I(E ;B ) =

∑

ℓ=1

(ℓ)

I(E

ℓ

) , (28)

as it was shown in (Ahrens et al., 2008). Hence, the

mutual information for a given sequence B and the

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

extrinsic LLR E is effected by the layer-speciﬁc char-

acteristics, i.e. the SNR and the mapping of the bits

to both the QAM symbols as well as to the layers, as

well as the layer speciﬁc parameters α

(ℓ)

7 RESULTS

The FEXT impact is in particular strong for short ca-

bles (Valenti, 2002). Therefore for numerical analysis

an exemplary cable of length l = 0.4km with n = 10

wire pairs is chosen. The wire diameter is 0.6mm

and hence a characteristic cable frequency of f

0.178MHz·km

is assumed. On each of the wire

pairs a multicarrier system with N = 10 subcarriers

was considered. The actual crosstalk circumstances

are difﬁcult to acquire and they vary from cable to ca-

ble. Therefore an exemplary mean FEXT coupling

constants of K

= 10

−13

.. . 10

−15

(Hz

· km)

−1

are

employed (Valenti, 2002; Aslanis and Ciofﬁ, 1992).

The average transmit power on each wire pair is sup-

posed to be P

= 1V

and as an external disturbance

a white Gaussian noise with power spectral density

is assumed. Identical systems on all wire pairs are

presumed (multicarrier symbol duration T

= 2µs, M-

ary QAM and a guard interval length of T

= T

/2).

Furthermore, the baseband channel of the multicarrier

system is excluded from the transmission in order to

provide this frequency range for analogue telephone

transmission. For a fair comparison the ratio of sym-

bol energy to noise power spectral density at the cable

output is deﬁned for the MIMO case (n > 1) accord-

ing to



+ T



+ (n−1)P

kfn

, (29)

with P

as mean power of the signal on the direct

paths at the cable output and P

kfn

as mean FEXT

signal power at the cable output (Ahrens and Lange,

2006). Using the constraint-length K = 3 NSC code

with the generator polynomials of (7,7,7,5) in oc-

tal notation, the performance is analyzed for an effec-

tive user throughput of 4 bit/s/Hz. Our results, ob-

tained by analyzing the soft-demapper characteristic

(Fig. 8), suggest that the performance of the MIMO-

OFDM system is strongly effected by the FEXT cou-

pling. Here it turns out that a heavy FEXT coupling

is highly beneﬁcial for a fast convergence in the low

SNR region as it is can be seen in Fig. 9. In general,

the achievable performance of the iterative decoder is

substantially affected by the speciﬁc mapping of the

bits to both the QAM symbols as well as to the layers.

While the employment of the classic Gray-mapping

is appropriate in the absence of a priori information,

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

extrinsic demapper output →

extrinsic decoder output →

NSC code with K = 3

= 10

−13

(Hz

·km)

−1

= 10

−15

(Hz

·km)

−1

Figure 8: Exit chart with anti-Gray mapping on all activated

layers at 10 log

/Ψ

) = 15 dB.

12 14 16 18 20

−3

−2

−1

10 ·lg(E

/Ψ

) (in dB) →

bit-error rate →

= 10

−13

(Hz

·km)

−1

= 10

−15

(Hz

·km)

−1

Figure 9: BER of the investigated system (solid line , un-

coded system using 4-QAM on all layers, dotted line , iter-

atively detected coded system (3 iterations) with anti-gray

mapping and 16-QAM on all layers, dashed line , itera-

tively detected coded system (10 iterations) with anti-gray

mapping and 16-QAM on all layers).

the availability of a priori information in iteratively

detecting decoders requires an exhaustive search for

ﬁnding the best non-Gray – synonymously also re-

ferred to as anti-Gray – mapping scheme (Chindapol,

2001). Investigations in (Ahrens et al., 2008) have

shown that layer-speciﬁc mapping schemes only offer

a slightly better performance at low SNRs. Therefore

throughout this work anti-gray mapping were used on

all layers. Our BER curves obtained by computer

simulations show that the overall BER performance

is strongly effected by both the FEXT coupling and

the number of iterations. Thereby the FEXT coupling

between neighbouring wire pairs seems to be a real

catalyst for the overall performance that is effected

FAR-END CROSSTALK IN ITERATIVELY DETECTED MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEMS

by both the cable length as well as the cable proper-

ties such as the type of isolation, the number of wire

pairs and the kind of combination of the wire pairs

within the binders.

8 CONCLUSIONS

In this contribution the FEXT impact in iteratively de-

tected MIMO-OFDM transmission schemes has been

studied. Our results show that FEXT is not neces-

sarily a limiting factor if appropriate signal process-

ing strategies are used. Our results show that a heavy

FEXT impact is overall beneﬁcial for a good conver-

gence behaviour at low SNR. Having hybrid optical

and electrical ﬁxed access networks with relatively

short copper cables (e. g. ﬁbre transmission up to

a street cabinet or a building and bridging the last

short drop by already installed twisted pair copper

cables), iteratively detected and SVD-aided MIMO-

OFDM transmission schemes seems to be a true alter-

native for delivering broadband services, when heavy

FEXT couplingsbetween neighbouringwire pairs can

be expected.

REFERENCES

Ahrens, A., K¨uhn, V., and Weber, T. (2008). Iterative De-

tection for Spatial Multiplexing with Adaptive Power

Allocation. In 7th International Conference on Source

and Channel Coding (SCC), Ulm.

Ahrens, A. and Lange, C. (2006). Optimal Power Allo-

cation in a MIMO-OFDM Twisted Pair Transmission

System with Far-End Crosstalk. In International Con-

ference on Signal Processing and Multimedia Appli-

cations (SIGMAP), Set´ubal (Portugal).

Aslanis, J. T. and Ciofﬁ, J. M. (1992). Achievable Infor-

mation Rates on Digital Subscriber Loops: Limiting

Information Rates with Crosstalk Noise. IEEE Trans-

actions on Communications, 40(2):361–372.

Bahai, A. R. S. and Saltzberg, B. R. (1999). Multi-Carrier

Digital Communications – Theory and Applications of

OFDM. Kluwer Academic/Plenum Publishers, New

York, Boston, Dordrecht, London, Moskau.

Bingham, J. A. C. (2000). ADSL, VDSL, and Multicarrier

Modulation. Wiley, New York.

Brink, S. t. (2001). Convergence Behavior of Iteratively

Decoded Parallel Concatenated Codes. IEEE Trans-

actions on Communications, 49(10):1727–1737.

Chindapol, A. Ritcey, J. A. (2001). Design, Analysis,

and Performance Evaluation for BICM-ID withsquare

QAM Constellations in Rayleigh Fading Channels.

IEEE Journal on Selected Areas in Communications,

19(5):944–957.

Forney, G. D., Gallager, R. G., Lang, G. R., Longstaff,

F. M., and Qureshi, S. U. (1984). Efﬁcient Modu-

lation for Band-Limited Channels. IEEE Journal on

Selected Areas in Communications, 2(5):632–647.

Galli, S. and Kerpez, K. J. (2002a). Methods of Sum-

ming Crosstalk From Mixed Sources—Part I: Theo-

retical Analysis. IEEE Transactions on Communica-

tions, 50(3):453–461.

Galli, S. and Kerpez, K. J. (2002b). Methods of Sum-

ming Crosstalk From Mixed Sources—Part II: Perfor-

mance Results. IEEE Transactions on Communica-

tions, 50(4):600–607.

Honig, M. L., Steiglitz, K., and Gopinath, B. (1990). Multi-

channel Signal Processing for Data Communications

in the Presence of Crosstalk. IEEE Transactions on

Communications, 38(4):551–558.

ITU-T Recommendation G.993.2 (2006). Very high speed

digital subscriber line transceivers 2 (VDSL2). Inter-

national Telecommunication Union, Geneva.

Kalet, I. (1987). Optimization of Linearly Equalized

QAM. IEEE Transactions on Communications,

35(11):1234–1236.

Kalet, I. (1989). The Multitone Channel. IEEE Transac-

tions on Communications, 37(2):119–124.

Kalet, I. and Shamai (Shitz), S. (1990). On the Capacity of

a Twisted-Wire Pair: Gaussian Model. IEEE Trans-

actions on Communications, 38(3):379–383.

Kreß, D. and Krieghoff, M. (1973). Elementare Ap-

proximation und Entzerrung bei der

Ubertragung von

PCM-Signalen ¨uber Koaxialkabel. Nachrichtentech-

nik Elektronik, 23(6):225–227.

Lange, C. and Ahrens, A. (2005). Effect of Far-End

Crosstalk in Multi-Pair Symmetric Copper Cables.

In XXI Krajowe Sympozjum Telekomunikacji (KST),

pages 181–190, Bydgoszcz (Poland).

Proakis, J. G. (2000). Digital Communications. McGraw-

Hill, Boston.

Raleigh, G. G. and Ciofﬁ, J. M. (1998). Spatio-Temporal

Coding for Wireless Communication. IEEE Transac-

tions on Communications, 46(3):357–366.

Raleigh, G. G. and Jones, V. K. (1999). Multivariate

Modulation and Coding for Wireless Communication.

IEEE Journal on Selected Areas in Communications,

17(5):851–866.

Valenti, C. (2002). NEXT and FEXT Models for Twisted-

Pair North American Loop Plant. IEEE Journal on

Selected Areas in Communications, 20(5):893–900.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications