ROTATION INVARIANT FEATURE EXTRACTION FOR

WATERMARKING

M. Scagliola and P. Guccione

Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, Via E. Orabona 4, 70125 Bari, Italy

Keywords:

Watermarking, Radon Transform, Rotation Invariant.

Abstract:

Many watermarks for still images are robust against common signal processing techniques, mainly JPEG

compression, noise adding and low-pass ﬁltering, while they are sensitive to geometrical manipulations, that

yield desynchronization errors.

In this paper robustness against some geometric transformations is achieved using a feature extraction method

based on the Radon transform and whose aim is to identify an unique (and robust) feature from the image

spectrum. The embedding, which exploits the extracted feature, is based on a multiplicative rule technique

and is applied on a suitable subset of the image Fourier transform. The properties of the extracted feature

allows to resynchronize the detector and the embedded watermark even if the image undergoes geometric

manipulations (in particular rotations) as well as other processings, so that the correct watermark retrieving is

guaranteed.

Experimental results, lead on many standard images, conﬁrm the effectiveness of the feature extraction method

and the robustness of the watermark against both processing and geometric transformations.

1 INTRODUCTION

Digital watermarking is a technique to hide an infor-

mation, called the watermark, into a cover media. Wa-

termark techniques play an important role in the copy-

right protection of multimedia such as images, sounds

and video. In a blind watermarking context, the detec-

tor must be able to detect the mark on a received im-

age that has undergone a certain number of unknown

manipulations of an unknown entity, without owning

any information about the original image.

While many watermarking methods perform well

against the common signal processing techniques

(mainly ﬁltering, noise adding and compression), they

lack robustness against geometric distortions, such as

rotation, scaling, translation, cropping/shearing, pro-

jective transformation, (Licks and Jordan, 2005). This

is justiﬁed by the different impact that these classes

of distortions have on the embedded watermark; in

fact, while the common signal processing techniques

reduce the watermark energy, geometric distortions

induce synchronization errors between the embedder

and the detector.

Geometric attacks can be both unintentional and

intentional; for example, an unintentional geometric

attack occurs when a marked image is printed and

scanned, as in the scanning process the image can be

slightly rotated with respect to the sampling grid. On

the other hand a geometric attacks can be performed

intentionally by an attacker with the aim of impair the

watermark detection, exploiting the weakness of the

watermarking system.

Therefore achieving robustness against geometric

transformations has become a widely studied topic in

digital image watermarking.

Several strategies have been proposed for water-

mark detection after geometric distortions. A rough

classiﬁcation divides these schemes into template in-

sertion, invariant domain based schemes and feature-

based algorithms (Licks and Jordan, 2005). Tem-

plates are registration patterns which are inserted into

the image in addition to the watermark, allowing the

synchronization of the embedder and detector. This

solution may reduce the image ﬁdelity and the wa-

termark capacity; moreover templates are susceptible

to removal or estimation attacks (Licks and Jordan,

2005). The Fourier-Mellin domain is often used in

watermarking since it is proved to be theoretically

invariant to rotation, scaling and translations (RST)

transformations. Thus, if the watermark is embed-

229

Scagliola M. and Guccione P. (2008).

ROTATION INVARIANT FEATURE EXTRACTION FOR WATERMARKING.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 229-235

DOI: 10.5220/0001931502290235

 SciTePress

ded into the Fourier-Mellin transform of an image,

the robustness with respect to these geometrical trans-

formations is provided (

ORuanaidh and Pun, 1998),

(Lin et al., 2001). Actually, as stated in (Lin et al.,

2001), the Fourier-Mellin transform is considered an

expensive solution to cope with RST attacks and the

problem of inverting this map is a quite difﬁcult task.

Feature-based algorithms are founded on the capabil-

ity to identify certain image features (edges, corners

and so on) before and after an attack. A huge vari-

ety of features have been used in several methods to

provide geometric robustness: for example Bas et al.

use a corner detector to construct a triangular tessel-

lation where the mark is embedded (Bas et al., 2000);

in (Simitopoulos et al., 2002) two one-dimensional

generalized Radon transforms are used; in (Xin et al.,

2004) an expansion of the image based on the Pseudo-

Zernike basis has been proposed with the properties

of RST invariance.

In this paper we present a watermarking technique

robust against rotation distortion and other common

signal processing, which is based on the capability

to extract a single invariant direction from the im-

age spectrum, used just to synchronize the detector

and the watermark. We start from the properties of

the Fourier-Mellin domain and from the well known

property of the 2D Fourier spectra, which states that

the Fourier transform (FT) of a rotated image is the

rotated version of the FT applied on the not-rotated

image. The idea is to properly deﬁne an insertion re-

gion in the Cartesian double transformed Fourier do-

main able to achieve rotation invariance avoiding the

need of a log-polar mapping, unlike in (

ORuanaidh

and Pun, 1998) and (Lin et al., 2001). Our approach

differs from other methods that embed the mark into

the Fourier domain since a single robust feature, ex-

tracted in this domain, is used to set up the rotation

invariant insertion region. Therefore, starting from

the detected invariant direction, the watermark is em-

bedded in a ring region covering the middle frequen-

cies in the Fourier domain using the rule described in

(Barni et al., 1998).

In the following we present a detailed description

of this method and experimental results that evidence

the effectiveness of the direction extraction and the

watermark retrieval under several distortions.

2 INVARIANT DIRECTION

The key idea is to characterize the invariant direction

as the straight line, passing for ( f

= 0, f

= 0), along

which the function |I( f

, f

)| has its maximum cumu-

lated value, where I( f

, f

) is the Fourier transform of

an image i(x,y). (Heretoafter it is intended that the

”zero” frequency location is ( f

= 0, f

= 0)). Hence

the invariant direction is uniquely identiﬁed by the an-

gle θ

inv

formed by the extracted line with a reference

direction. From the previous deﬁnition it can be in-

ferred that the Radon transform (Toft, 1996) is the

fundamental tool for the extraction of the invariant

feature.

The placement of the invariant direction in the

Fourier domain is motivated by two reasons. Since

the embedding is performed in the Fourier domain,

it is a rationale to extract a synchronization feature

in the same domain. Moreover, a watermarked im-

age can undergo attacks modifying either the whole

image or circumscribed part of it, hence the Fourier

domain has the advantage that local modiﬁcations in

the spatial domain are always spreaded.

The invariant direction is used as resynchroniza-

tion feature, which enables the watermarking system

to identify the same direction from every distorted

′

( f

, f

); in this way, whether the image has been ro-

tated by an angle α, the invariant direction (θ

inv

+ α)

is extracted, so that the detector and the message will

always be synchronized.

Actually the problem is that the extraction of the

invariant direction is performed both at the embed-

ding and detection sides; between the two operations

the cover image could have been modiﬁed by channel

distortions (which includes intentional distortions). In

order to make the extraction method as robust as pos-

sible, a pre-processing step is then applied to the im-

age to get a spectrum (and so, at least partially, an im-

age) which is as less dependent as possible on these

modiﬁcations.

2.1 Image Pre-processing

The pre-processing is performed to get a spectrum

which is less dependent on the modiﬁcations that the

image can undergo; its effect is then to provide ro-

bustness to the direction extraction method.

To get an image representation invariant to chan-

nel modiﬁcations, the edge feature is pointed out,

since edges generally survive (even if distorted) to

several distortions and processings. In Fig. 1 the pre-

processing chain scheme is fully depicted.

The tool used for the edge extraction is the cas-

cade of a Gaussian low-pass ﬁltering and a morpho-

logical gradient, i.e. a morphological operator reveal-

ing sharp luminance transitions. This cascade is quite

similar to a Laplacian of a Gaussian ﬁltering, usually

adopted for edge extraction, being the Laplacian op-

erator here substituted by the morphological gradient

operator (Lee et al., 1987). However differences be-

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

230

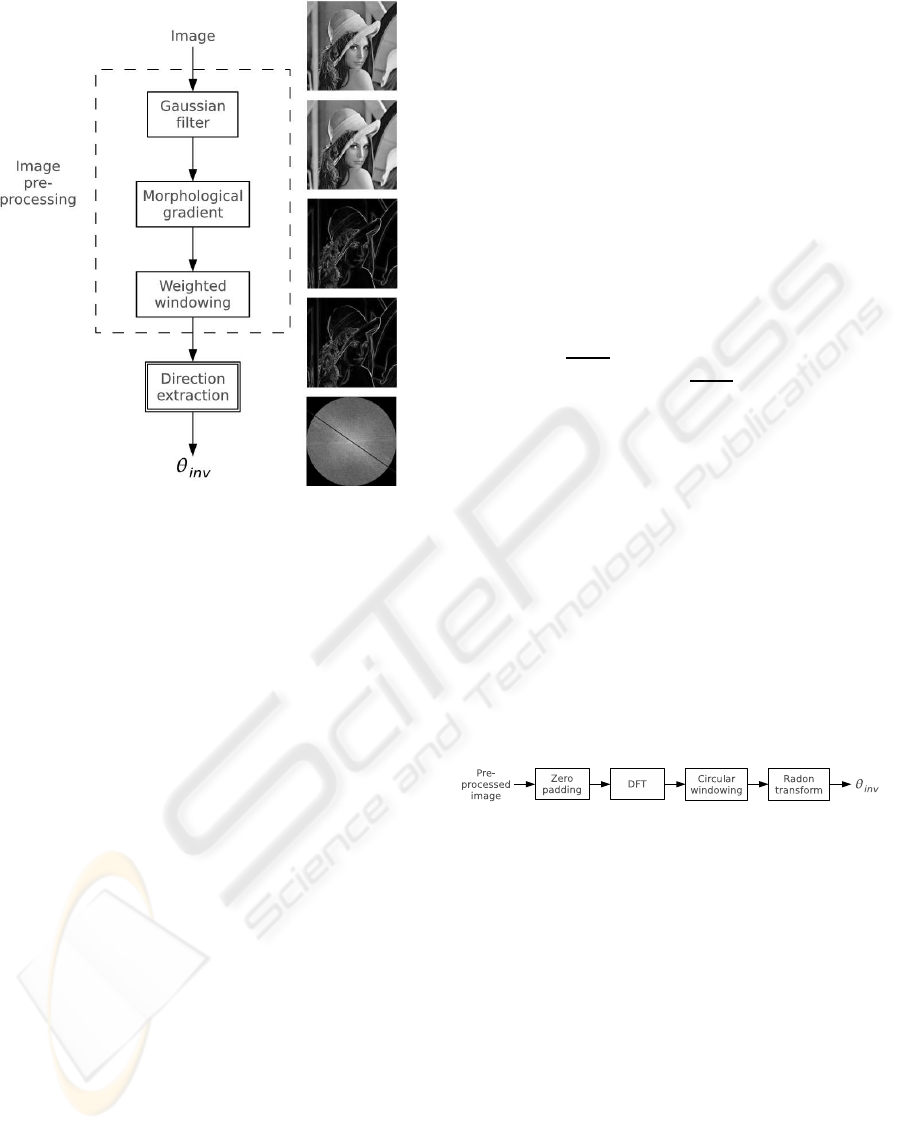
Figure 1: Block diagram of the pre-processing.

tween the twos exist. Laplacian operator associates

zero-crossing of second derivatives to an edge, whose

location is as close as possible to the real edge (Gon-

zalez and Woods, 2002), and it is typically followed

by a thresholding to convert a gray-scale image into a

binary edge image. By the way in this application we

are not interested in an accurate location of edges with

a binary image but rather in an invariant (and possibly

robust against noise) feature extraction through edge

enhancement; moreover we are interested to produce

edges with thickness as invariant as possible to modi-

ﬁcations on image. For this purpose a Gaussian low-

pass ﬁltering together with a suitable morphological

gradient operator, able to enhance and to widen the

edges, can ﬁt as well.

Referring to Fig. 1, the image is ﬁrstly low-pass

ﬁltered by a Gaussian ﬁlter, in order to reduce the

higher frequencies energy, which in detection could

be due to noise added by the channel; then the mor-

phological gradient of the image is computed. The

chosen morphological structuring element has size 5

and has a symmetry as close as possible to a circular

one.

The effects on the image spectrum of the mor-

phological operations are not straightforward because

of their non-linear nature. An intuitive explanation

is that edge sharpening yields an increase of both

low frequencies and frequency terms related to edges,

hence the global effect is comparable to a contrast en-

hancement on image spectrum, which is a modiﬁca-

tion useful for the direction extraction method.

The circular symmetric windowing is performed

on the enhanced edge image to reduce aliasing effects

in the discrete Fourier domain. In fact the FT and

the rotation are operations that do not exactly com-

mute in a discrete domain (Stone, H.S. and Tao, B.

and McGuire, M., 1998), so we do not expect a per-

fect identity between the rotated version of the DFT of

the image and the DFT computed from the the rotated

image. These differences are due to the skew between

the directions along which aliasing takes place and

the directions of FT axes. The aliasing effects can be

just reduced smoothing the boundaries with a circular

and symmetric window (Stone, H.S. and Tao, B. and

McGuire, M., 1998). The adopted windowing func-

tion has unit value within the circumference of radius

= (k

/2)

√

N ·M and is zero outside the circumfer-

ence of radius r

= (k

/2)

√

N ·M, with a raised co-

sine connection in the middle region; N and M are the

image dimensions.

In our application, we have chosen empirically the

parameters values k

= (4/5) and k

= (1/5) process-

ing a standard image database.

2.2 Invariant Direction Extraction

Method

In the diagram depicted in Fig. 2 the processing chain

constituting the invariant direction extraction method

is shown. These operations are performed on the

pre-processed image as obtained from the processing

chain presented in subsection 2.1.

Figure 2: Block diagram of the direction extraction method.

The image is ﬁrstly checked to have the same di-

mensions; if N 6= M, the shortest dimension is padded

with zeroes to obtain a square matrix before the com-

puting of the DFT.

Invariant direction extraction is performed using

the Radon transform on the transformed image. The

Radon transform is thus computed over directions

passing through the zero frequency:

R(0,ϕ)[ f(x,y)] =

∞

−∞

∞

−∞

f(x,y)δ(y−x tan(ϕ)) dxdy (1)

Actually a Discrete Radon transform is computed

on the image DFT, using a simple sum approxima-

tion. The Radon transform on a ﬁnite rectangular do-

main does not consider that, on different lines, dif-

ROTATION INVARIANT FEATURE EXTRACTION FOR WATERMARKING

231

ferent amounts of pixels lie and consequently diag-

onals are privileged directions, causing mistaken es-

timation. The circular windowing before the Dis-

crete Radon Transform can prevent this effect since

along every line a ﬁxed amount of non-zero terms lies

(Jafari-Khouzani and Soltanian-Zadeh, 2005).

Computing of Radon transform in a discrete con-

text implies that a ﬁnite set of direction equally spaced

between [0,π[ must be chosen: ϕ

= i · ∆ϕ, i =

0,1,··· ,(⌊π/∆ϕ⌋−1).

Eq. (1) can be rearranged

R(0,i)[|I( f

, f

)|] =

= ∆f

N−1

∑

k=0

|I(k∆ f

,tan(ϕ

)k∆f

)| (2)

where ∆f

and ∆ϕ set the sampled lines along which

the cumulated value of Radon transform are com-

puted. Since the Cartesian grid of ( f

, f

), for which

the DFT values are available, will generally not coin-

cide with the grid (k∆f

,tan(ϕ

)k∆f

), a linear 2D in-

terpolation is used to compute the values of |I( f

, f

in the needed positions.

After the computing of the discrete Radon trans-

form, the invariant direction angle θ

inv

will be equal

to the ϕ

for which

inv

= max

∈[0,π[

{R(0,i)[|I( f

, f

)|]} (3)

occurs.

3 EMBEDDING AND DETECTION

The embedding of the message is performed in the

Fourier domain using the embedding method de-

scribed in (Barni et al., 1998). The message is in-

serted into a sorted subset of the coefﬁcients of the

doubly transformed domain, obtained as the intersec-

tion of a circular crown region with a ﬁnite subset of

straight lines belonging to a sheaf:

( f

, f

)t.c.











min

≤ ( f

+ f

) ≤ R

max

= tan(θ

inv

+ i·∆θ) · f

i = 0, ··· ,(⌊π/∆θ⌋−1)

(4)

where θ

inv

is the invariant direction extracted in (3).

Thus the detector and the embedder are synchronized,

since they consider the straight lines belonging to the

sheaf in an ordered sequence starting with the same

one, indexed by θ

inv

. From the previously deﬁned

insertion region, an ordered sample sequence is ex-

tracted and the mark is inserted into this, according to

the chosen rule and according to the symmetry prop-

erties of the Fourier transform. For the embedding

too, a linear 2D interpolation is needed to get the val-

ues of the image in the locations belonging to the

above-deﬁned sheaf.

According to (Barni et al., 1998), the message

W = {w

,··· ,w

} consists of a pseudo-random se-

quence, each value w

being a random real number

with normal distribution, zero mean and unitary vari-

ance. The multiplicative embedding rule is

′

= t

+ g w

| (5)

where g is a gain factor modulating the embedding

strength.

Since the DFT of a real signal is complex val-

ued, the embedding of the same message will be per-

formed twice, both in real and imaginary parts of the

DFT samples, taking care to preserve the complex

conjugate symmetry of the spectrum.

The detector is built so that, given an image in in-

put, once the invariant direction has been extracted,

it can retrieve the marked sample sequence. Then the

detector veriﬁes what message has been inserted com-

puting a correlation coefﬁcient between the marked,

and possibly corrupted, sample sequence extracted

from the image and every codeword belonging to a

shared watermark codebook, known both at embed-

der and at detector sides. The correlation coefﬁcient

will be used as measure of the mark presence at the

detector.

4 RESULTS

Herein some experimental results are shown, obtained

processing standard images, whose size is typically

512x512 pixels.

The effectiveness of the direction extraction

method is a needed condition for the decoder and

the mark to be synchronized. The following results

were obtained computing the Radon transform of the

windowed DFT of a pre-processed image along a ﬁ-

nite set of directions equally spaced with a step ∆ϕ =

0.5 deg and choosing the direction with the maximum

cumulated value, as described in section 2.

In Figs. 3(a)–(d) the right working of the proposed

direction extraction method is exhibited. In Fig. 3(a)

the pre-processed Lena image is depicted while in

Fig. 3(b) its windowed spectrum is shown and the

extracted invariant direction is highlighted. Rotating

by an angle of 30 deg the Lena image, we had the

pre-processed image and the windowed spectrum de-

picted respectively in Figs. 3(c) and 3(d). Comparing

the highlighted directions in Figs. 3(b) and 3(d), the

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

232

rotation of the invariant direction according to the ro-

tation of the original image is noticeable.

(a) Pre-processed image (b) Invariant direction

image

(d) Invariant direction

Figure 3: Example of pre-processing on Lena image with

extraction of invariant direction for both original and rotated

cases.

In order to measure the effectiveness of the direc-

tion extraction method, we compared the extracted in-

variant directions before and after the embedding and

attacks. We tested the algorithm against both com-

mon signal processing techniques (Additive White

Gaussian Noise, JPEG compression and smoothing)

and geometric distortions (rotation, scaling and crop-

ping). Cropping attack was performed cutting away

both symmetrically and asymmetrically the framing

part of the marked image, but preserving the image

center (where the most relevant information is sup-

posed to be located).

The experimental results are listed in Table 1,

where ∆θ

inv

= θ

′

inv

−(θ

inv

+ α)mod π is the difference

of extracted directions at the detection and embedding

sides. The angle values are expressed in deg, while

the results for cropping attacks are indexed by the per-

centage of pixels constituting the cropped image with

respect to the original one.

Besides, the direction extraction method performs

well against random line removal attack too (experi-

mental results here are not shown).

Afterwards some experiments were performed

to evaluate the effectiveness of the whole embed-

ding/detection scheme. We embedded a mark se-

Table 1: Invariant directions extracted from attacked im-

ages.

Image Lena Peppers Boat

Invariant direction 145 173.5 113.5

Attack ∆θ

inv

∆θ

inv

∆θ

inv

AWGN

σ = 10 -0.5 0 0

σ = 15 -0.5 0 0

σ = 20 0 0 0

JPEG

quality= 50 -0.5 0 0

quality= 30 0 0 0

quality= 20 0 0 0

quality= 10 0 0 0

Smoothing

Average 0 0 0

Gaussian 0 0 0

Median 0 0 0

Rotation

α = 1 0 0 0

α = 5 -0.5 -0.5 0

α = 45 -0.5 -1 -0.5

α = 60 -0.5 -0.5 -0.5

α = 90 -0.5 0 0.5

α = 120 -0.5 -0.5 0

α = 160 0 -0.5 -0.5

α = −1 0 0 0

α = −5 -0.5 -0.5 0

α = −45 -0.5 -1 -0.5

α = −60 -0.5 -0.5 0

α = −90 -0.5 0 0.5

α = −120 -0.5 -0.5 -0.5

α = −160 0 1 0

Scaling

scale= 0.5 1.5 0.5 0

scale= .75 1.5 0 0

scale= 1.5 0 0 0.5

scale= 2 0 0.5 0

Cropping

rem% = 85 1.5 0 0

rem% = 78 1.5 0 0

rem% = 65 -2.5 0 0

rem% = 53 -2.5 0 0

quence of length 9800 samples along 70 directions

into the DFT domain and the gain factor in the em-

bedding rule was ﬁxed at the value g = 1.

In order to evaluate the imperceptibility of the wa-

termarking method, the adopted distortion metric is

the often used peak to signal noise ratio (PSNR). The

PSNR has been computed for the images in database

embedding 1000 different watermarks. For the pro-

cessed images we computed the average PSNR, that

resulted to be always greater than 40 dB and its stan-

dard deviation which was in the range .1 to .2 dB.

To check the robustness of the whole system,

some gray scale standard images were watermarked

and both signal processing and geometric attacks

were applied to these images. The detector output

reveals the estimated embedded message as the one

having the greatest correlation coefﬁcient with the

sample sequence extracted from the marked and pos-

sibly corrupted image. Thus, from the detector re-

ROTATION INVARIANT FEATURE EXTRACTION FOR WATERMARKING

233

sponse to all the codewords belonging to the code-

book, we measured the ﬁrst-to-second peak ratios

) in decibel.

In the experimental results, listed in Table 2, the

index ˜n represents the codeword retrieved from the

attacked image by comparison of the correlation co-

efﬁcients. These results were obtained processing the

standard image Boat, but similar results have been ob-

tained with other standard images. Here the results for

the cropping attack are related only to symmetrical

cuts of the framing part of the marked image, since

for asymmetrical cropping the watermark retrieving

have shown to fail.

Table 2: Detection results on the attacked image Boat.

Embedded codeword index n = 259

Correlation detector

Attack ˜n P

(dB)

AWGN

σ = 10 259 3.99

σ = 15 259 4.61

σ = 20 259 4.38

JPEG

QF= 50 259 3.64

QF= 30 259 3.38

QF= 20 259 2.61

Smoothing

Average 259 3.35

Gaussian 259 3.55

Median 259 3.15

Rotation

α = 1 259 3.73

α = 5 259 3.82

α = 45 259 3.69

α = 60 259 2.22

α = 90 259 3.69

α = 120 259 3.75

α = 160 259 1.98

α = −1 259 3.83

α = −5 259 3.56

α = −45 259 4.05

α = −60 259 4.66

α = −90 259 3.69

α = −120 259 4.18

α = −160 259 4.26

Scaling

scale= 0.5 Fail -

scale= .75 Fail -

scale= 1.5 Fail -

scale= 2 Fail -

Cropping

rem% = 85 259 4.50

rem% = 78 259 4.08

rem% = 65 259 3.35

rem% = 53 259 2.95

By inspection of the results listed in Table 2 it

is veriﬁed the robustness of the proposed scheme

against almost all the tested attacks. In particular the

correct mark retrieving is guaranteed even if a slight

error in extracted direction occurs. However the wa-

termark recovering fails if the marked image is scaled

up or down, though the invariant direction is correctly

retrieved (see Table 1). This is due to the inability

of the embedding/detection method to cope with the

transformed domain enlargement resulted from the

image scaling.

5 CONCLUSIONS

In this paper, a watermarking system has been pro-

posed that is robust against both processing and geo-

metric attacks, with particular reference to rotations.

A feature extraction method based on Radon trans-

form has been explained; this method is able to re-

trieve from image spectra a direction that is invariant

to geometric transformations on the image. This fea-

ture is used to synchronize the detector and the region

in the 2D DFT domain wherein the watermark is in-

serted, guaranteeing the watermark recovering.

Experimental results demonstrate the robustness

of both the invariant direction and the watermark em-

bedding against common processing and many of ge-

ometric attacks.

Achieving robustness against scaling attacks by an

improvement of the embedding method is even possi-

ble. Authors are still working in this direction, to-

gether with the testing of the robustness after com-

bined attacks.

REFERENCES

Barni, M., Bartolini, F., Cappellini, V., and Piva, A. (1998).

A dct-domain system for robust image watermarking.

Signal Process., 66(3):357–372.

Bas, P., Chassery, J.-M., and Macq, B. M. (2000). Robust

watermarking based on the warping of predeﬁned tri-

angular patterns. In Proc. SPIE Vol. 3971, Security

and Watermarking of Multimedia Contents II, pages

99–109.

Gonzalez, R. C. and Woods, R. E. (2002). Digital image

processing. Prentice Hall.

Jafari-Khouzani, K. and Soltanian-Zadeh, H. (June 2005).

Rotation-invariant multiresolution texture analysis us-

ing radon and wavelet transforms. Image Processing,

IEEE Transactions on, 14(6):783–795.

Lee, J., Haralick, R., and L.G., S. (1987). Morphological

edge detector. Robotics and Automation, IEEE Trans-

actions on, 3(2):142–153.

Licks, V. and Jordan, R. (July-Sept. 2005). Geometric at-

tacks on image watermarking systems. Multimedia,

IEEE, 12(3):68–78.

Lin, C.-Y., Wu, M., Bloom, J., Cox, I., Miller, M., and Lui,

Y. (May 2001). Rotation, scale, and translation re-

silient watermarking for images. Image Processing,

IEEE Transactions on, 10(5):767–782.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

234

ORuanaidh, J. J. and Pun, T. (1998). Rotation, scale and

translation invariant spread spectrum digital image

watermarking. Signal Process., 66(3):303–317.

Simitopoulos, D., Koutsonanos, D., and Strintzis, M.

(2002). Image watermarking resistant to geometric at-

tacks using generalized radon transformations. Digital

Signal Processing, 2002. DSP 2002. 2002 14th Inter-

national Conference on, 1:85–88 vol.1.

Stone, H.S. and Tao, B. and McGuire, M. (1998). Analy-

sis of image registration noise due to rotationally de-

pendent aliasing. Technical Report TR 98-018, Nec

Research Institute Tech. Rep.

Toft, P. (1996). The Radon Tranform - Theory and Imple-

mentation. PhD thesis, Department of Mathematical

Modelling, Technical University od Denmark.

Xin, Y., Liao, S., and Pawlak, M. (2-5 May 2004). Ge-

ometrically robust image watermarking via pseudo-

zernike moments. Electrical and Computer Engineer-

ing, 2004. Canadian Conference on, 2:939–942 Vol.2.

ROTATION INVARIANT FEATURE EXTRACTION FOR WATERMARKING

235