
ESTIMATING H.264/AVC VIDEO PSNR WITHOUT REFERENCE
Using the Artificial Neural Network Approach
Martin Slanina and V
´
aclav
ˇ
R
´
ı
ˇ
cn
´
y
Department of Radio Electronics, Brno University of Technology, Purky
ˇ
nova 118, Brno, Czech Republic
Keywords:
H.264/AVC, video quality, no reference assessment, PSNR, artificial neural network.
Abstract:
This paper presents a method capable of estimating peak signal-to-noise ratios (PSNR) of digital video se-
quences compressed using the H.264/AVC algorithm. The idea is in replacing a full reference metric - the
PSNR (for whose evaluation we need the original as well as the processed video data) - with a no reference
metric, operating on the encoded bit stream only. As we are working just with the encoded bit stream, we can
spare a significant amount of computations needed to decode the video pixel values. In this paper, we describe
the network inputs and network configurations, suitable to estimate PSNR in intra and inter predicted pictures.
Finally, we make a simple evaluation of the proposed algorithm, having the correlation coefficient of the real
and estimated PSNRs as the measure of optimality.
1 INTRODUCTION
As the video processing, storage and transmission
systems began to shift from the analog to the digital
domain, the quality assessment and evaluation meth-
ods had to be changed accordingly. For analog video,
several well defined and quite easily measurable pa-
rameters sufficed to give a clue on the visual quality
of the video material at the consumer end. For digital
video, the visual quality at the end of the communi-
cation chain depends not only on the system charac-
teristics itself, but – to a considerable extent – on the
video content. Especially for digital video compres-
sion techniques, content is what really matters.
As the human observer is commonly the consumer
of the video material, it is his judgement that is the
ideal measure of video quality. However human ob-
servers may be and are used in the so-called subjective
quality tests, there has been a great effort to substitute
subjective assessment with an objective approach, i.e.
a technique to measure the video quality automati-
cally.
Basically, the objective approaches differ in the
extent to which the original video material is avail-
able at the quality measurement (receiver) point. In
case of full reference quality evaluation, we have full
access to the original material, which is the most de-
sirable, but at the same time the most uncommon con-
figuration. If we have some limited information about
the original, we are talking about reduced reference
assessment. The worst case (and unluckily the most
common) scenario is when only the processed video,
subject to faults, compression artifacts or other degra-
dation, is available for quality assessment. What we
are trying to do is replace a full reference metric with
a no reference approach, i.e. to remove the necessity
of having the original material available.
The area of full reference metrics is quite well un-
derstood and lots of metrics have been developed to
perform quality assessment of this kind. The sim-
plest pixel-based metrics only compare the two video
sequences with simple mathematical operations (Wu
and Rao, 2006; Wang et al., 2004), while the more so-
phisticated try to make a model of the human visual
system in order to catch the most important phenom-
ena such as contrast sensitivity, masking, etc. (Win-
kler, 2005; Daly, 1992). However, although some of
the metrics perform reasonably well, the peak signal-
to-noise ratio holds its position in many application
and is still used as a performance measure.
On the other hand, the no reference video quality
assessment area has still a lot to improve. It is quite
straightforward that for no reference quality assess-
ment of a compressed video material, typical com-
pression artifacts shall be used. It is true for the com-
pression algorithms such as MPEG-2, where block ar-
tifact and blur detection can give a solid ground for
quality judgement (Fischer, 2004; Marziliano et al.,
244
Slanina M. and
ˇ
Rí
ˇ
cný V. (2008).
ESTIMATING H.264/AVC VIDEO PSNR WITHOUT REFERENCE - Using the Artificial Neural Network Approach.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 244-250
DOI: 10.5220/0001932502440250
Copyright
c
SciTePress
2002). For the H.264/AVC, however, such detection
is complicated by the fact that there is an adaptive de-
blocking filter at the end of the encoding chain, which
prevents the block artifacts from appearing in the de-
compressed material. It is thus difficult, if not impos-
sible, to rely on artifact detection when assessing the
H.264/AVC video. In our approach, we will use pa-
rameters describing the decoding process which are
directly present in the bit stream to feed an artifi-
cial neural network. A similar approach for MPEG-2
compressed video was presented in (Gastaldo et al.,
2002).
2 PSNR AS A QUALITY
MEASURE
The peak signal-to-noise ratio is a very simple full ref-
erence quality metric. It is given by an equation (Win-
kler, 2005)
PSNR = 10log
10
m
2
MSE
, [dB] (1)
where m is the maximum value a pixel can take and
MSE is the mean squared error, given by
MSE =
1
T XY
T
∑
k=1
X
∑
i=1
Y
∑
j=1
[ f (k, i, j) −
˜
f (k, i, j)]
2
(2)
for a video sequence consisting of T frames of M × N
pixels. The symbols f (k,i, j) and
˜
f (k, i, j) represent
the luma pixel values of the original and the distorted
video, respectively.
3 H.264/AVC ENCODING
PARAMETERS
As noted above, we will use a set of parameters
extracted from the H.264/AVC bit stream for qual-
ity assessment. In order to understand their mean-
ing, let us now briefly describe the operation of an
H.264/AVC encoder. The standard describes only the
decoder (ITU-T, 2005), but the encoder configuration
we will discuss is very likely to appear in most re-
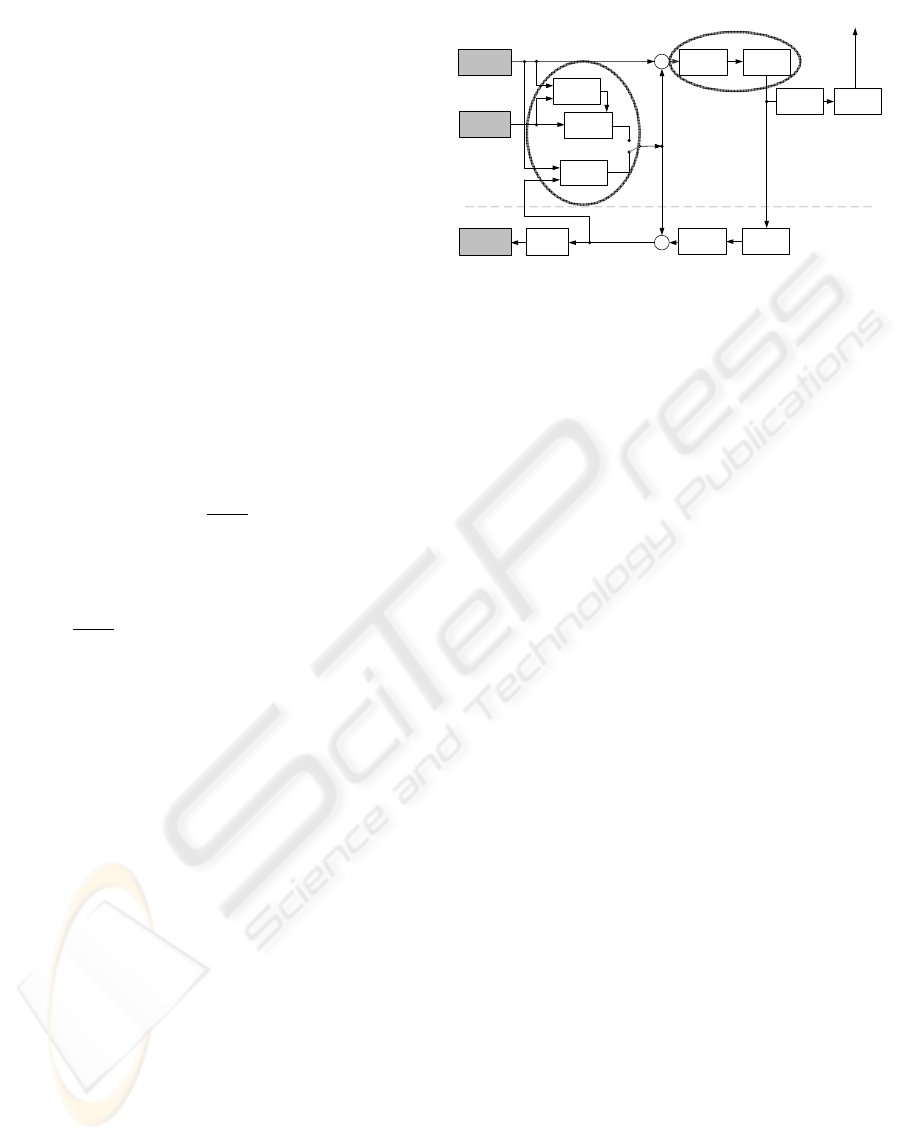
alizations. A typical structure of an H.264/AVC en-
coder is shown in Fig. 1. At the input of the encoder,
we have the current frame (or field) to be encoded and
a reference frame. The encoder maintains a list of ref-
erence frames and one or more of them may be used
for prediction. The encoder now has to decide what
type of prediction to use: Intra prediction uses only
the pixel data within the same frame, while inter pre-
diction uses different frame image data with motion
Network
Abstraction
Layer - NAL
Current
frame
Reference
frame
Motion
estimation
Motion
compensation
Intra
prediction
Filter
Reordering
QuantizationTransform
Entropy
encoder
Inverse
quantization
Inverse
transform
Reconstructed
frame
Inter prediction
Intra prediction
+
-
+
+
Figure 1: H.264/AVC encoder structure.
compensation. Furthermore, for intra as well as inter
prediction, different modes can be selected. The pre-
diction process is marked with the left oval in Fig. 1.
A mode detailed description of the available predic-
tion modes will follow in subsection 3.1
After forming the prediction, residuals remain to
be encoded. There are several transforms available
in the H.264/AVC (Richardson, 2003), whose coeffi-
cients are subsequently quantized and encoded in the
bit stream. More on the transform and quantization
will follow in subsection 3.2. This process is marked
with the right oval in Fig. 1.
Below the dashed line in Fig. 1, there is a return
path in the encoder. Every encoded picture is de-
coded as well, in order to provide a reference for fur-
ther prediction of subsequent pictures. This is where
the above mentioned adaptive deblocking filter can be
found, preventing the block artifacts from appearing
and making artifact detection such a difficult issue for
H.264/AVC.
It is the prediction mode and the quantization
coarseness that we use for video image quality esti-
mation.
3.1 Prediction Modes
As noted above, the encoder has the option to choose
between intra and inter prediction for every mac-
roblock. Furthermore, for each of these prediction
types, there is a whole list of modes to choose from
in order to achieve the optimal quality – compression
tradeoff.
For intra prediction, each macroblock can be pre-
dicted either as one 16 × 16 block, four 8 × 8 blocks
or sixteen 4 × 4 blocks (ITU-T, 2005). Furthermore,
one special prediction mode can be used – the IPCM
mode – where no prediction is done and the pixel val-
ues are encoded directly, which may be beneficial in
some situations. It should be mentioned that not all
modes are available in all encoder profiles. The 8 × 8
mode is, for example, only used in the high profile
ESTIMATING H.264/AVC VIDEO PSNR WITHOUT REFERENCE - Using the Artificial Neural Network Approach
245

of H.264/AVC. While encoding larger blocks needs
fewer bits to signal the prediction process to the de-
coder, more energy is likely to remain in the residuals.
For example, if the encoder is limited with bit rate
constraints, it may happen that large blocks are pre-
dicted in order to spare bits even though high energy
residuals will remain for the transform.
For inter prediction, even more options are avail-
able. One macroblock may be predicted as one
16 × 16 blocks, two 16 × 8 or 8 × 16 blocks or four
8 × 8 blocks. If the 8 × 8 mode is chosen, the four
macroblock partitions may be split up in additional
four ways. There is one more mode – the direct mode
– where no additional information is transmitted and
the macroblock is simply copied from the reference
picture. Again, the predicted block size is likely to
carry a significant amount of information on the en-
coding performance.
3.2 Quantization
In the H.264/AVC, the transform coefficients are
quantized using scalar quantization. This is another
part of the encoding process, where the resulting qual-
ity can be strongly influenced. The basic forward
quantizer operation is (Richardson, 2003)
Z
i, j
= round(Y
i, j
/Qstep), (3)
where Y
i, j
are the transform coefficients, Qstep is a
quantizer step size and Z
i, j
are the quantized coeffi-
cients. A total of 52 Qstep values are supported by
the standard, indexed by a quantizing parameter.
We will make use of the quantizing parameter val-
ues to predict video image PSNR in section 4.
4 ESTIMATING PSNR VALUES
In the previous text, we discussed the parameters di-
rectly available in the H.264/AVC bit stream, which
may give us a clue on the quality of the decoded
video. Let us now use these parameters to develop an
algorithm capable of estimating PSNR values without
reference. For simplicity, we will only consider base-
line profile to verify the correctness of our approach.
There are two important features of the baseline pro-
file we have to consider at this time – the baseline
profile does not use 8 × 8 intra prediction and motion
compensated inter prediction is done only in one di-
rection, from one reference picture.
4.1 Video Sequence Set
We constructed two sets of short video sequences
in CIF resolution (352 x 288 pixels). The CIF for-
mat was selected just to verify the correctness of our
approach. Extension for other formats will then be
straightforward. One set is used for training of the
artificial neural network (training set), the other one
is used to evaluate the trained network and check
its generalization ability (evaluation set). The un-
compressed sequences are freely available (CIF Se-
quences, 2006). The two sets were constructed in or-
der to have various types of sequences (with differ-
ent spatial and temporal activity) in each of the sets.
First frames of the sequences for the test set and the
evaluation set are shown in Fig. 2 and Fig. 3, respec-
tively. Each sequence was encoded and decoded in
H.264/AVC baseline profile, with four different bit
rate settings of the encoder. The VBR encoder setting
was selected, and consequently the quantizing param-
eter remained unchanged within the slices.
Figure 2: Video sequences used for network training.
Figure 3: Video sequences used for evaluation.
4.2 Intra Coded Pictures
We have already stated that for intra coded pictures,
the prediction is done only from the neighboring pix-
els within the same picture. More exactly, predic-
tion is done from image data within the same slice (a
defined group of macroblocks). As we take the pre-
dicted block size as an input to our algorithm, we have
four parameters as inputs: no. of macroblocks coded
in 16 × 16 mode, no. of macroblocks coded in 8 × 8
mode, no. of macroblocks coded in 4 × 4 mode and
no. of IPCM macroblocks. We will experiment with
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
246
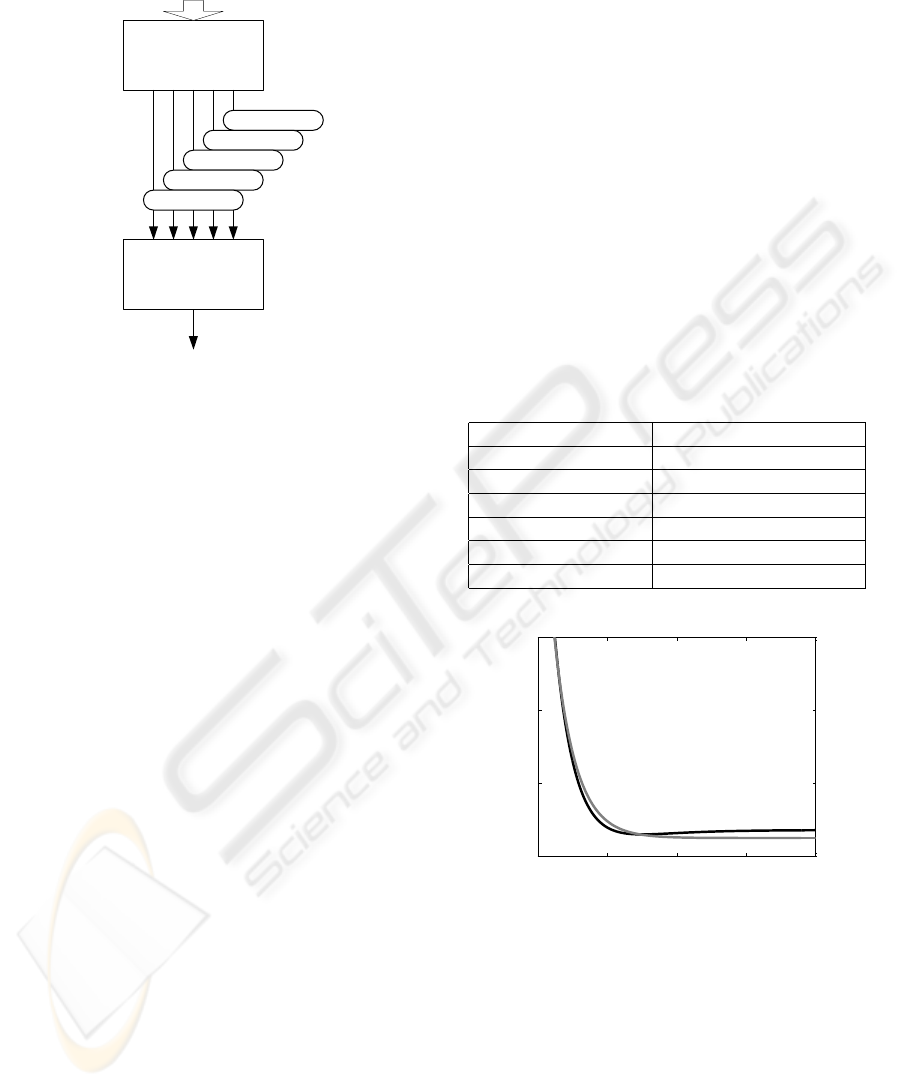
101101010000111000011101000010010011
010101010111110001101101011010010101
H.264/AVC encoded bit stream
Parameter
Extractor
16x16 blocks
8x8 blocks
4x4 blocks
IPCM blocks
Quant. par.
Artificial
Neural
Network
Estimated PSNR
Figure 4: Predicting PSNR for intra coded pictures.
artificial neural networks to estimate PSNR values us-
ing these parameters. As it is desirable to have all the
inputs normalized in the range 0 to 1 for the artificial
neural network, we divide all the values by the total
number of macroblocks within the picture. One more
input to the artificial neural network will be formed
by the quantizing parameter. Again, to stay in the
range 0 to 1, it will be divided by the factor of 52
as it is the maximum value the quantizing parameter
can take. The algorithm will then operate as shown
in Fig. 4. The scheme takes all the possible modes
into account. For the baseline profile we are using,
the 8 × 8 bocks are not used and the IPCM blocks are
not likely to appear, for instance.
The first block in the scheme is a Parameter Ex-
tractor, supposed to read the numbers of the respec-
tive prediction modes from the bit stream. For this,
we use a modified H.264/AVC reference decoder in
the version JM11 (Suehring, 2006).
4.2.1 Linear Network
As the simplest configuration, we experimented with
an artificial neural network consisting of neurons with
linear transfer function only. It is known that any
feedforward configuration of linear neurons can be re-
placed with an equivalent made up of a single neuron,
thus one neuron unit suffices to exploit the capabilities
of linear network for our application (Bishop, 2006).
We trained the linear neuron unit on the training
set of video sequence intra frames using the gradi-
ent descent (least mean squares) algorithm (Bishop,
2006). This algorithm is designed to minimize the
mean of squared errors over the set of training exam-
ples. We used five different encoder configurations
over the ten different training sequences, resulting in
50 training examples. The training process is shown
in Fig. 5 – the graph shows how the mean squared
errors decrease for the training set with the increas-
ing training iterations (epochs) and how it develops
for the evaluation set. Fig. 6 shows how the corre-
lation coefficient of the real and the estimated PSNR
changes during the training. After 2500 epochs we
reached a correlation coefficient of 0.9774 for the
training set and 0.9666 for the evaluation set. The
trained network weights are listed in Table 1 for all
the input parameters scaled in the range 0 to 1. As the
IPCM and 8 × 8 blocks are not used in our configura-
tion, the corresponding weights are equal to zero. The
corresponding scatter plot diagram for the evaluation
set is shown in Fig. 7.
Table 1: Linear unit weigths for intra picture PSNR predic-
tion. Baseline profile.
Input parameter Corresponding weight
Quantizing par. / 52 -47.53
IPCM blocks 0
16 × 16 blocks 26.22
8 × 8 blocks 0
4 × 4 blocks 17.37
bias 43.60
0 500 1000 1500 2000
0
5
10
15
Training epochs [-]
Mean squared error [-]
Evaluation set
Training set
Figure 5: Linear unit training.
4.2.2 Multi-Layer Network
We experimented with several configurations of
multi-layer networks as well, having a variable (1 to
5) sigmoid units in the hidden layer and one linear
unit in the output layer. The correlation coefficients
we reached for the evaluation set were very close to
those achieved by the linear network. However, the
implementation of such networks is rather more com-
plex and thus in the rest of our considerations we will
only estimate PSNRs of intra predicted frames using
the linear unit as described above.
ESTIMATING H.264/AVC VIDEO PSNR WITHOUT REFERENCE - Using the Artificial Neural Network Approach
247
0 500 1000 1500 2000
0.7
0.75
0.8
0.85
0.9
0.95
1
Training epochs [-]
Correlation coefficient [-]
Evaluation set
Training set
Figure 6: Correlation coefficient with increasing number of
training epochs.
15 20 25 30 35 40 45 50
15
20
25
30
35
40
45
50
Real PSNR [dB]
Estimated PSNR[dB]
Figure 7: Scatter plot diagram: Estimated versus real
PSNRs for intra coded pictures after 2500 training epochs
(evaluation picture set).
4.3 Inter Coded Pictures
To estimate PSNR for inter coded pictures, we will
have to consider more parameters than in the previ-
ous situation as for the inter predicted pictures more
prediction methods are available.
Intra prediction can still be used in inter predicted
pictures, so we will keep the parameters (per cent of
block types) defined in section 4.2 and displayed in
Fig. 4. In addition, we will use the information of the
size of intra predicted blocks, i.e. how many blocks
were predicted with each of the available block sizes
from 16 × 16 down to 4 × 4 (see section 3.1).
As the pixel values are predicted from other pic-
tures, the PSNR of the predicted picture certainly de-
pends on the PSNR of the reference picture. There is
a whole list of pictures the H.264/AVC decoder may
use for prediction and a decision on the reference pic-
ture choice is done for each inter predicted block sep-
arately. This means the PSNR of the reference is typ-
ically changing throughout the predicted picture. Our
solution is to compute the average PSNR for each of
the inter prediction modes.
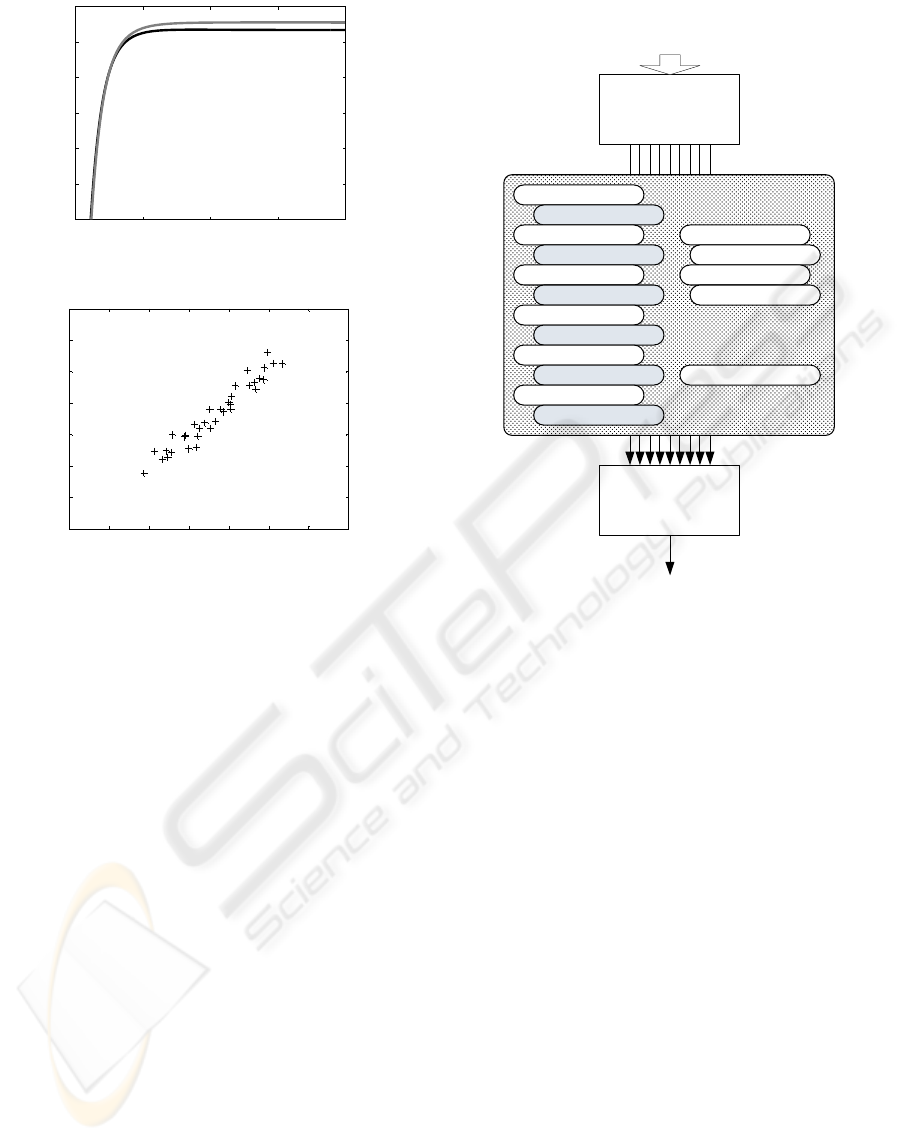
The system configuration for the inter predicted
pictures is then as shown in Fig. 8. Obviously, the
101101010000111000011101000010010011
010101010111110001101101011010010101
H.264/AVC encoded bit stream
Parameter
Extractor
Artificial
Neural
Network
Estimated PSNR
16x16 intra blocks
8x8 intra blocks
4x4 intra blocks
IPCM blocks
Quant. par.
16x16 inter blocks
16x16 ref PSNR
16x8 inter blocks
16x8 ref PSNR
8x8 inter blocks
8x8 ref PSNR
8x4 inter blocks
8x4 ref PSNR
4x4 inter blocks
4x4 ref PSNR
Direct blocks
Direct ref PSNR
Figure 8: Predicting PSNR for inter coded pictures.
number of network input parameters has grown sig-
nificantly.
4.3.1 Network Training
To estimate the PSNR of inter coded pictures, we tried
to use a linear network first, similarly to the case in
section 4.2.1. However, in the case of inter predicted
pictures, the problem can not be described by a linear
network and thus the network could not be trained to
predict PSNR values correctly.
A multi-layer network is then the next choice. For
the network training, we always need the PSNR of the
reference picture the prediction is done from. In the
training process, we can still use the real PSNRs to
achieve the best performance of the trained network.
In the network performance evaluation, its own es-
timated PSNRs will be used as the refence PSNRs
(PSNR of the picture the prediction is done from).
We used four network configurations, having one
to five sigmoid (tansig) units in the hidden layer
and one linear unit in the output layer. The net-
works were trained using the backpropagation algo-
rithm with Bayesian regularization to avoid overfit-
ting (Bishop, 2006). The training was done for 500
epochs with a learning rate of 0.0005. We used 60
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
248

20 25 30 35 40 45 50
20
25
30
35
40
45
50
Real PSNR [dB]
Estimated PSNR [dB]
Figure 9: Scatter plot diagram: Estimated versus real
PSNRs for inter coded pictures afted 500 training epochs
(evaluation picture set).
0 10 20 30 40 50 60
25
30
35
Frame no.
PSNR
0 10 20 30 40 50 60
32
34
36
38
Frame no.
PSNR
Estimated
Real
Estimated
Real
Figure 10: Real and estimated PSNR for two video se-
quences (first 60 frames).
frames of each compressed video sequence.
4.3.2 Network Performance
Fig. 9 shows the scatter plot diagram of the real end
estimated PSNRs for the first 60 frames of the evalua-
tion set sequences each compressed with five different
configurations, the network has three sigmoid units in
the hidden layer and one linear unit in the output layer.
The correlation coefficient is 0.9306.
In Fig. 10 we show how the real and estimated
PSNRs develop in time for two sequences from the
evaluation set. It is obvious the overall accuracy of
the estimation vastly depends on how exactly we are
able to estimate the PSNR of the first (intra) frame
in the sequence. Even though PSNR for some of the
sequences was estimated quite closely, sequences re-
main in the evaluation set for which the differences
are significant.
5 CONCLUSIONS
We have presented a method to estimate peak signal-
to-noise ratios for H.264/AVC video sequences with-
out reference. As the simplest configuration, we con-
sidered H.264/AVC baseline profile and worked with
low resolution video sequences.
We reached a correlation of 0.9666 for intra pre-
dicted pictures (linear network) and 0.9306 for in-
ter predicted pictures (network with 3 sigmoid units
in the hidden layer and one linear unit in the output
layer). Increasing the number of hidden units in the
network for inter PSNR prediction led to a decrease
of MSE over the training set, but also the correlation
for the evaluation set decreased.
Even though the correlation is quite high, a closer
estimate is still desired as the PSNR is a logarithmic
measure and even a few decibel differences may rep-
resent quite big differences in quality.
The network weights and biases are only learned
for a certain encoder implementation. When migrat-
ing to a system using a different encoder, the networks
should be trained again for the given encoder.
Our considerations were limited to the baseline
profile only. For other profiles, bi-directional predic-
tion has to be taken into account and the PSNR of the
reference pictures has to be included in the estimation
process.
ACKNOWLEDGEMENTS
This paper was financially supported by the Czech
Grant Agency under grant No. 102/08/H027 ”Ad-
vanced methods, structures and components of elec-
tronics wireless communication” and by the research
program MSM 0021630513 ”Electronic Communica-
tion Systems and Technologies of New Generation”
(ELCOM).
REFERENCES
Bishop, C. M. (2006). Pattern Recognition and Machine
Learning. Springer, New York. ISBN 0-387-31073-8.
CIF Sequences (2006). [online]. Retrieved December 2006
from http://trace.eas.asu.edu/yuv/cif.html.
Daly, S. J. (1992). The visible difference predictor: an al-
gorithm for the assessment of image fidelity. In Proc.
SPIE: Human Vision, Visual Processing, and Digital
Display III, volume 1666, pages 2–15.
Fischer, W. (2004). Digital Television: A Practical Guide
for Engineers. Springer, Berlin. ISBN 3-540-01155-2.
ESTIMATING H.264/AVC VIDEO PSNR WITHOUT REFERENCE - Using the Artificial Neural Network Approach
249

Gastaldo, P. et al. (2002). Objective assessment of MPEG-
2 video quality. Journal of Electronic Imaging,
11(3):365–374.
ITU-T (2005). Recommendation H.264. Advanced video
coding for generic audiovisual services. The Interna-
tional Telecommunication Union, Geneva.
Marziliano, P. et al. (2002). A no-reference perceptual blur
metric. In Proceedings of the International Confer-
ence on Image Processing, volume 3, pages 57–60.
Richardson, I. E. G. (2003). H.264 and MPEG-4 Video
Compression. Wiley, Chichester (England). ISBN 0-
470-84837-5.
Suehring, K. (2006). The h.264/MPEG-4 AVC reference
software – jm11. [online]. Retrieved November 2006
from http://iphome.hhi.de/suehring/tml/download/.
Wang, Z., Lu, L., and Bovik, A. C. (2004). Video qual-
ity assessment based on structural distortion measure-
ment. Signal Processing: Image Communication,
19(2):121–132.
Winkler, S. (2005). Digital Video Quality: Vision Models
and Metrics. Wiley, Chichester. ISBN 0-470-02404-6.
Wu, H. R. and Rao, K. R. (2006). Digital Video Image Qual-
ity and Perceptual Coding. Taylor & Francis, Boca
Raton. ISBN 0-8247-2777-0.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
250
