NOVEL DIGITAL DIFFERENTIATOR AND CORRESPONDING
FRACTIONAL ORDER DIFFERENTIATOR MODELS
Maneesha Gupta, Pragya Varshney
Advanced Electronics Lab, Division of Electronics and Communication Engineering
Netaji Subhas Institute of Technology, Sector-3, Dwarka, New Delhi 110075, India
G. S. Visweswaran
Department of Electrical Engineering, Indian Institute of Technology
Hauz Khas, New Delhi 110016, India
B. Kumar
Department of Computer Engineering, Maharaja Surajmal Institute of Technology
Janakpuri, New Delhi110058, India
Keywords: Al-Alaoui operator, Hsue et al. operator, differentiator, fractional order differentiator, continued fraction
expansion.
Abstract: This paper proposes a novel first order digital differentiator. The differentiator is obtained by linear mixing
of Al-Alaoui operator (Al-Alaoui, 1993) and wide band differentiator (Hsue, 2006). MATLAB simulation
results of the proposed differentiator for various sampling frequencies have been presented. The magnitude
results are in close conformity to the theoretical results for approximately 78% of the full range. The phase
of the new differentiator is almost linear, with a maximum phase error of 8.24º. We have also proposed new
operator based fractional order differentiator models. These models are obtained by performing the Taylor
series expansion and continued fraction expansion of the proposed operator. Comparisons of the suggested
models with the existing models of half differentiators show perceptible improvement in performance of the
fractional order circuit. MATLAB simulation results show that the magnitude response of the proposed half
differentiator matches with the theoretical results of continuous-time domain half differentiator for almost
the whole frequency range and the phase approximates a constant group delay which is desirable for many
applications. The major purpose of this paper is to emphasize that fractional order control systems are better
than the conventional order systems as the system control performance is enhanced.
1 INTRODUCTION
There are many design approaches for obtaining
digital differentiators. Al-Alaoui (Al-Alaoui, 1995)
used Simpson’s rule to develop stable differentiators.
In another paper (Al-Alaoui, 1993), Al-Alaoui has
used a linear combination of Simpson’s rule and
trapezoidal rule to develop differentiator models.
Tseng (Tseng, 2001) has proposed the design of
fractional order digital FIR differentiator by solving
linear equations of Vandermonde form and in
(Tseng, 2007), he has proposed the design of FIR
and IIR fractional order Simpson digital integrators
using binomial series expansion. Zhao et al. (Zhao et
al., 2005) have proposed a method for design of
fractional order FIR differentiators in frequency
domain and have presented simulation results to
validate their technique. In (Bhattacharya and
Antoniou, 1995), Bhattacharya et al. have designed
digital differentiators using neural networks. B.
Kumar et al. (Kumar and Roy, 1988), (Kumar and
Roy, 1989), (Reddy et al., 1991) have designed
digital differentiators for low, high and midband
frequencies respectively. Khan et al. (Khan et al.,
2004) have proposed higher degree FIR
differentiators based on Taylor series expansion. In
(Hsue et al., 2004), the bilinear rule is modified to
develop 1
st
and 2
nd
order having operating
frequencies larger than 10 GHz. Schneider et al.
47
Gupta M., Varshney P., S. Visweswaran G. and Kumar B. (2008).
NOVEL DIGITAL DIFFERENTIATOR AND CORRESPONDING FRACTIONAL ORDER DIFFERENTIATOR MODELS.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 47-54
DOI: 10.5220/0001933500470054
Copyright
c
 SciTePress

(Schneider et al., 1991) have proposed new 2
nd
and
higher order stable s-to-z mapping functions and
explored the sources of error in the higher order
mapping functions. Work on fractional order
systems has been done in (Chen and Moore,
2002),(Chen and Vinagre, 2003),(Xue and Chen,
2002),(Varshney et al., 2002).
In this paper, a new first order s-to-z
transformation is proposed which is obtained by
using the Al-Alaoui operator and the Hsue et al.
operator. The idea was to linearly mix two well
known approaches to obtain a differentiator which
would also follow the ideal differentiator for a large
range of frequencies. Both differentiators being of
first order and approximating the ideal differentiator
for a large range of frequencies, the proposed
differentiator results are found to be in close
conformity with those of the ideal differentiator. The
differentiator models are developed for different
values of sampling frequency and their performance
compared. The half differentiator models obtained
by discretization of the proposed operator are
developed and their performance compared with
existing half differentiator models (Chen and Moore,
2002) as well as the theoretical result of continuous-
time domain half differentiator. MATLAB
simulation results are presented to validate the
effectiveness of the proposed operator and its
differentiator models.
The paper is organized as follows: the new
operator is proposed in Section 2. In Section 3, we
have developed the fractional order differentiator
models for
21s =
. In Section 4, the MATLAB
simulation results of the proposed operator and the
half differentiators are presented and compared with
their ideal counter parts. Section 5 concludes the
paper.
2 PROPOSED NEW OPERATOR
The Al-Alaoui operator based integrator in z-domain
is
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
=
−
−
1
1
al
z1
7z1
8
T7
)z(H
(1)
and the integrator obtained by inverting the
transformation of a wide-band differentiator in
(Hsue, 2006) is
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
=
−
−
1
1
Hsue
z1
z1658.01
2
T
)z(H
(2)
where
T
is the sampling period.
To obtain a differentiator that fits better the ideal
differentiator over the entire normalized frequency
band, linear mixing of Al-Alaoui differentiator and
the wide-band differentiator is performed. The
procedure is as follows: first, the transfer functions
of the two integrators of eqns. (1, 2) are linearly
mixed as in eqn. (3).
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
α−+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
+
α=
α−+α=
−
−
−
−
)z1(
)7z1(
8
T7
)1(
)z1(
)z1658.01(
28.0
)z(H)1()z(H
)z(H
1
1
1
1
al
Hsue
new
(3)
where
α
, (
10 <α<
) determines the contribution of
each operator in the new operator.
Second, the transfer function of eqn. (3) is
inverted and the resulting transfer function of the
new digital differentiator is
)T04205.012495.0()T375.0875.0(z
)1z(
)z(G
new
α−+α−
−
=
(4)
Using Jury’s stability criterion, the different-
tiator
)z(G
new
was found to be stable for the condi-
tion
;25.2
T
<α
)10(
<
α
<
∀
. Choosing
s05.0
T
=
,
(sampling frequency =
2 *1 T 125.7rad/ sec
π
=
),
the transfer function of the new differentiator is:
)21025.012495.0()01875.0875.0(z
)1z(
)z(G
new
α−+α−
−
=
(5)
Now,
α
is varied from
1 to 0
in increments of 0.1.
The magnitude response of the proposed
differentiator is plotted for different values of
α
as
shown in Fig 1.
Figure 1: Magnitude response of new operator for various
α with T=0.05s.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
48

The percentage relative magnitude error of the new
differentiator is compared with the magnitude
response of the ideal differentiator and plotted in Fig
2.
Figure 2: Relative magnitude error as compared to the
continuous-time differentiator for various α .
Observations show that best matching with ideal
differentiator were for
0.9.
α
=
The error is within
2% upto 0.84 of the Nyquist frequency. Fig 3
shows the phase of the new differentiator for
different
α
. The response is almost linear with a
maximum phase of
o
24.8 at 55.0 of the Nyquist
frequency. The ideal linear phase corresponds to an
ideal differentiator with half a sample of delay.
These results are comparable with those of Al-
Alaoui operator based differentiator as suggested in
(Al-Alaoui, 1993).
Figure 3: Phase of new operator for various α and
corresponding linear phase differentiator and phase error
for α=0.9.
Using four values of
T
viz. 0.05s, 0.00625s,
0.001s and 0.000625s, and with 0.9,
α
= the
transfer functions of the new differentiator are:
Figure 4: Magnitude response of new operator for
different T.
)1434.0z(
)1z(1901.23
)z(G
s05.0T
1
+
−
=
=
(6)
)1428.0z(
)1z(263.1126
)z(G
s001.0T
2
+
−
=
=
(7)
)1428.0z(
)1z(0131.182
)z(G
s00625.0T
3
+
−
=
=
(8)
)1428.0z(
)1z(4141.1814
)z(G
s000625.0T
3
+
−
=
=
(9)
Figure 5: Magnitude error (in dB) as compared to the
continuous-time differentiator for different T.
The magnitude response of eqns. (6-9) are
plotted and compared with the magnitude of ideal
differentiator (Fig 4). The relative magnitude errors
are plotted in dB in Fig 5 and in percentage in Fig 6.
The phase response of the new differentiator and the
relative phase error is plotted in Fig 7.
NOVEL DIGITAL DIFFERENTIATOR AND CORRESPONDING FRACTIONAL ORDER DIFFERENTIATOR
MODELS
49

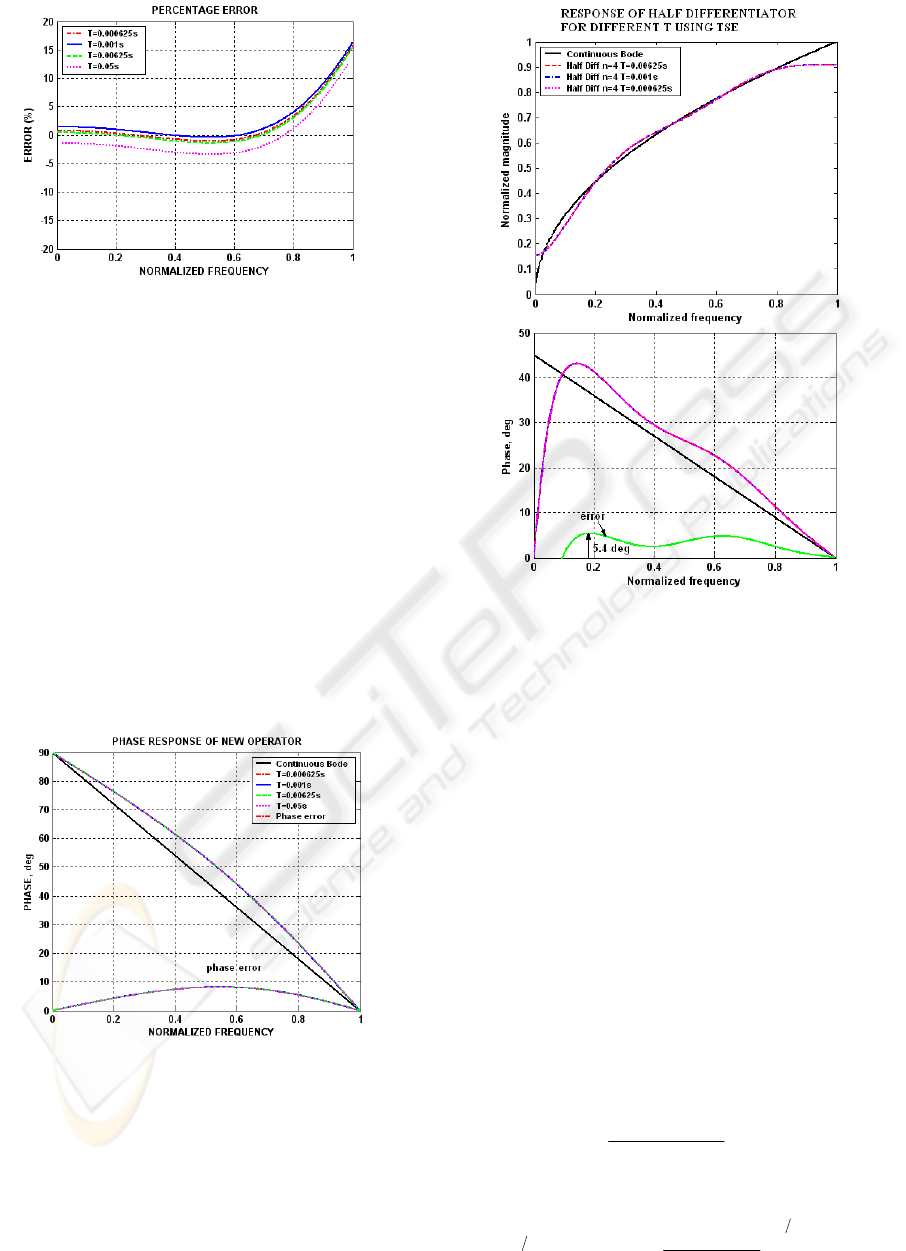
Figure 6: Relative magnitude error (in percentage) for
different T.
3 FRACTIONAL ORDER
DIFFERENTIATOR MODELS
Next the fractional order differentiator models based
on the proposed operator are suggested.
Discretization is the key step in the digital
implementation of the fractional order controller
containing
r
s where ();rR∈ 01.r<< The
discretization of fractional order differentiator can
be expressed by a generating function
)z(s
1−
ω= .
The generating function is used for obtaining the
coefficients and the form of the approximation
(Chen and Moore, 2002).
Figure 7: Phase response for different T, corresponding
linear phase differentiator and phase error.
In this paper, we have developed the models of
half differentiator for various sampling periods using
direct discretization method. We have discretized the
fractional order derivative using Taylor series
expansion (TSE) and continued fraction expansion
(CFE).
Figure 8: Response of half differentiator obtained by
Taylor series expansion of the new operator for different
values of T.
In the first method, the TSE of the numerator and
denominator polynomials of the transfer function of
eqns. (6-9) are performed. Truncating the length of
the numerator and denominator expansions, the
approximate models of half differentiator for
5to3n
=
are obtained. In the second method,
continued fraction expansion technique is used to
expand the new operator. The continued fraction
expansion uses the MATLAB command ‘cfrac’
(Chen and Moore, 2002), to obtain the models of
half differentiator for
5to3n
=
by collecting the
coefficients of the numerator and denominator
polynomials.
3.1 Discretization of New Operator
using Taylor Series Expansion
The proposed new operator for
s001.0
T
=
is
)1428.0z(
)1z(263.1126
s
+
−
=
(10)
For half differentiator
21
21
1428.0z
1z
263.1126s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
(11)
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
50

Expanding the above eqn. (11) using Taylor
series expansion the first 11 terms of the expansion
are
11 10 9 8 7
6543
2
11
11 10 9
876
5
z 0.5z 0.125z 0.0625z 0.0391z
0.0273z 0.0205z 0.0161z 0.0131z
0.0109z 0.0093 0.008
()
4.0301e-12z -3.268e-11z 2.6925e-10z
-2.627e-9z 1.9503e-8z -1.7384e-7z
1.6232e-6z -1
z
Gz
⎛⎞
−− − −
⎜⎟
−− −−
⎜⎟
⎜⎟
−−−
⎝⎠
=
+
+
+
43
2
.624e-5z 1.8197e-4z
-0.0025z 0.0714z 1
⎛⎞
⎜⎟
⎜⎟
⎜⎟
+
⎜⎟
⎜⎟
++
⎝⎠
(12)
Truncating the length of the expansion, the third
order half differentiator model is
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−+
−−−
=
0001819.0z002499.0z07136.0z
094.2z189.4z75.16z51.33
G
23
23
3
(13)
Figure 9: Percentage magnitude error for half
differentiator obtained by Taylor series expansion of the
new operator for different values of T.
Similar method is used to obtain the half
differentiator models for
0.00625 ,Ts=
s000625.0
(Table I). Fig 8 shows the magnitude
response and the group delay for the models of half
differentiators obtained using TSE for various
sampling frequencies. The relative error in phase is
also shown in the same figure. The relative
magnitude error in percentage is given in Fig 9.
3.2 Discretization of New Operator
using Continued Fraction
Expansion
The transfer functions of eqns. (6-9) are expanded
with
5.0r = using continued fraction expansion to
obtain the half differentiator models. The half
differentiator models for
s00625.0,s001.0
T
=
and
s000625.0
are listed in Table 1. The magnitude
response and group delay for the models of half
differentiators obtained using CFE are plotted for
various sampling frequencies in Fig 10. The relative
error in phase is also plotted in Fig 10. The relative
magnitude error (in percentage) is given in Fig 11.
Figure 10: Response of half differentiator obtained by
continued fraction expansion of the new operator for
different values of T.
4 SIMULATION RESULTS
In this paper, a new operator is proposed by linear
mixing of Al-Alaoui operator and the Hsue et al.
operator. The half differentiator models obtained by
discretization of the new operator using Taylor
series expansion and continued fraction expansion
are also suggested.
The magnitude and phase response of the
proposed differentiator are compared with the
responses of the ideal differentiator and MATLAB
simulation results have been presented to validate
the effectiveness of the proposed approach.
Fig 4 shows the magnitude response of proposed
differentiator for
s00625.0,s001.0T
=
and
NOVEL DIGITAL DIFFERENTIATOR AND CORRESPONDING FRACTIONAL ORDER DIFFERENTIATOR
MODELS
51

0.000625 .
s
The results are compared with the
response of ideal differentiator and it matches with
the theoretical results for approximately
%78 of the
frequency range for different sampling frequencies.
In Fig 5, the magnitude error is plotted in dB. From
the plot, it is observed that the best performance is
obtained for
s000625.0
T
=
as error is less than
dB40 upto 73.0 of the Nyquist frequency. The
results for
s00625.0
T
=
are good for the range
from
,0 to 0.74 excepting 62.0 to 36.0 of the
Nyquist frequency.
Figure 11: Percentage magnitude error for half
differentiator obtained by CFE of the new operator for
different values of T.
For
s001.0
T
=
, the operational range is limited
to the middle frequency range from
69.0 to 2.0 of
the Nyquist frequency range. Fig 6 shows the
magnitude error in percentage for different sampling
frequencies. Fig 7 shows the phase response of the
proposed differentiator for different sampling
frequencies. It can be seen that the proposed
operator has linear phase response with a maximum
error of
2.8 deg at 55.0 of the Nyquist frequency.
From the MATLAB simulation results of the half
differentiator (Fig 8, 10), it is observed that the
magnitude of the models obtained using continued
fraction expansion are in close conformity to the
theoretical results of half differentiator in
continuous-time domain for the full range of
frequencies and the phase approximates a constant
group delay which is desirable for many applications.
The percentage error in magnitude of half
differentiator (Fig 9, 11) obtained by continued
fraction expansion of the proposed operator is less
than
%5.0 for the entire range of frequency. Fig 8,
10 reveal that the CFE based models of half
differentiator give constant group delay for wider
range of frequency
(0.03 to 1 of the Nyquist
frequency) as compared to the TSE based half
differentiator models
(0.15 to 1 of the Nyquist
frequency). Moreover the error in phase is less in the
CFE based half differentiator models.
In Figs. 12, 13 we present the comparison of the
response of the new operator based fifth order half
differentiator models with the existing model of fifth
order half differentiator based on Al-Alaoui operator
for
s001.0
T
=
. It is observed that the performance
of the new operator based half differentiators is
better than that of the Al-Alaoui operator based half
differentiator.
Figure 12: Comparison of magnitude responses (for n=5)
of existing half differentiator based on Al-Alaoui operator,
the proposed operator and the continuous-time domain
half differentiator for T=0.001s.
Figure 13: Group delays of the existing half differentiator
based on Al-Alaoui operator, and the proposed operator.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
52

5 CONCLUSIONS
In this paper, two well known approaches have been
used to develop a new first order s-to-z mapping
function. The proposed operator was found to be
stable for various sampling frequencies and the
magnitude results matched with the ideal
differentiator upto
%78 of the Nyquist frequency.
The phase of the proposed operator also
approximates a linear phase of half a sample of
delay with a maximum error of
°24.8 at 55.0 of
the Nyquist frequency.
The half differentiator models obtained by
discretization of the proposed operator using
continued fraction expansion exhibit better
performance in terms of magnitude and phase as
compared to those obtained by Taylor series
expansion. The above mentioned results of half
differentiator validate the effectiveness of the
proposed operator. Such modeling finds application
in discrete realization of fractional order circuits.
In this paper, z-domain stable models of fractional
order differentiators (
r
s ) have been presented for
r=0.5. This method can be further extended to
obtain z-domain stable models based on the
proposed operator for different
r.
REFERENCES
M. A. Al-Alaoui, “Novel digital integrator and
differentiator”, Electronic Letters, Vol. 29, No. 4, pp.
376-378, 1993.
C. W. Hsue, L. C. Tsai and Y.H. Tsai, “Time Constant
Control of Microwave Integrators Using Transmission
lines,” Proc. of IEEE Trans. Microwave Theory and
Techniques, Vol. 54, No. 3, pp. 1043-1047, 2006.
M. A. Al-Alaoui, “A class of second order integrators and
low pass differentiators,” IEEE Transactions Circuits
and Systems I, vol. 42, pp. 220-223, Apr. 1995.
C. C. Tseng, “Design of fractional order digital FIR
differentiators,” IEEE Signal Processing letters, Vol. 8,
No. 3, pp. 77-79, 2001.
C. C. Tseng, “Design of FIR and IIR fractional order
Simpson digital integrators,” Proc. Signal Processing,
Elsevier: Science Direct, Vol. 87, No. 5, pp. 1045-
1057, 2007.
H. Zhao; G. Qiu; L. Yao; J. Yu, “Design of fractional
order digital FIR differentiators using frequency
response approximation,” Proc. International
Conference on Communications, Circuits and Systems,
2005. Vol. 2, 27-30 May 2005, pp. 1318-1321.
D. Bhattacharya, A. Antoniou, “Design of digital
differentiators and Hilbert transformers by feedback
neural networks,” Proc. IEEE Pacific Rim Conference
on Communications, Computers, and Signal
Processing, 1995, 17-19 May 1995, pp. 489 – 492.
B. Kumar, S.C. Dutta Roy, “Design of digital
differentiators for low frequencies,” Proc. IEEE, Vol.
76, No. 3, March 1988, pp. 287 – 289.
B. Kumar, S.C. Dutta Roy, “Maximally linear FIR digital
differentiators for high frequencies,” IEEE
Transactions on Circuits and Systems, Vol. 36, No.
6, June 1989, pp. 890 – 893.
M. R. R. Reddy, S. C. Dutta Roy, B. Kumar, “Design of
efficient second and higher degree FIR digital
differentiators for midband frequencies,” IEE
Proceedings-G, Vol. 138, No. 1, February 1991, pp.
29-33.
I. R. Khan, M. Okuda, R. Ohba, “Higher degree FIR
digital differentiators based on Taylor series,” 2004
47th Midwest Symposium on Circuits and Systems,
2004. MWSCAS '04, Vol. 2, 25-28 July 2004, pp. II-
57 - II-60.
C. W. Hsue, L. C. Tsai, and K. L. Chen, “Implementation
of first order and second order microwave
differentiators,” IEEE Trans. Microwave. Theory and
Techniques, Vol. 52, No. 5, pp. 1443-1448, 2004.
A. M. Schneider, J. T. Kaneshige, and F. D. Groutage,
“Higher order s-to-z mapping functions and their
application in digitizing continuous-time filters,” Proc.
IEEE, Vol. 79, pp. 1661-1674, 1991.
Y. Q. Chen and K.L. Moore, “Discretization schemes for
fractional-order differentiators and integrators,” IEEE
Trans. on Circuits and Systems - 1: Fundamental
Theory and Applications, Vol. 49, No. 3, pp. 363-367,
2002.
Y. Q. Chen, and B.M. Vinagre, “A new IIR-type digital
fractional order differentiator,” Elsevier Journal on
Signal Processing: Special issue on fractional signal
processing and applications, Vol. 83, No. 11, pp. 2359
– 2365, 2003.
D. Xue and Y. Q. Chen, “A Comparative Introduction of
Four Fractional Order Controllers,” Proceedings of
the 4th World Congress on Intelligent Control and
Automation, June 10-14, 2002, Shanghai, P.R.China,
pp. 3228-3235.
P. Varshney, M. Gupta and G. S. Visweswaran, “Higher
Degree Half Order Differentiators and Integrators,”
Proceedings of the 2nd International Conference on
Embedded Systems, Mobile Communication and
Computing, Aug, 3-5, 2007, Bangalore.
NOVEL DIGITAL DIFFERENTIATOR AND CORRESPONDING FRACTIONAL ORDER DIFFERENTIATOR
MODELS
53

Table 1: Half differentiator models obtained by using CFE and TSE on the proposed operator.
T HALF DIFFERENTIATOR MODELS USING
TAYLOR SERIES EXPANSION
HALF DIFFERENTIATOR MODELS USING
CONTINUED FRACTION EXPANSION
0.001s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−+
−−−
=
0001819.0z002499.0
2
z07136.0
3
z
094.2z189.4
2
z75.16
3
z51.33
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++−
−+−
=
0204.0z143.0
2
z
3
z
273.1z23.21
2
z74.52
3
z56.33
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+−+
−−−−
=
5e623.1z0001819.0
2
z002499.0
3
z07138.0
4
z
31.1z094.2
2
z19.4
3
z75.16
4
z51.33
4
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−++−
−−−−
=
007076.0z005755.0
2
z49.0
3
z429.1
4
z
06951.0z244.7
2
z11.4
3
z12.67
4
z56.33
4
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−+−−+
−+
−−−
−−
=
6e623.1z5e623.1
2
z0001818.0
3
z002499.0
4
z07138.0
5
z
9143.0z311.1
2
z092.2
3
z193.4
4
z75.16
5
z51.33
5
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+−−
+−
++−
+−
=
001369.0z02122.0
2
z1226.0
3
z201.1
4
z857.1
5
z
1337.0z302.1
2
z55.20
3
z13.67
4
z51.81
5
z56.33
5
G
0.00625s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−+
−−−
=
0001819.0z002499.0
2
z07136.0
3
z
8432.0z687.1
2
z745.6
3
z49.13
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++−
−+−
=
0204.0z143.0
2
z
3
z
5116.0z536.8
2
z2.21
3
z49.13
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+−+
−−−−
=
5e623.1z0001819.0
2
z002499.0
3
z07138.0
4
z
5276.0z8431.0
2
z687.1
3
z745.6
4
z49.13
4
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−++−
−−+−
=
007076.0z005755.0
2
z49.0
3
z429.1
4
z
02795.0z912.2
2
z52.16
3
z98.26
4
z49.13
4
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−+−−+
−+
−−−
−−
=
6e623.1z5e623.1
2
z0001818.0
3
z002499.0
4
z07138.0
5
z
3681.0z5276.0
2
z842.0
3
z688.1
4
z744.6
5
z49.13
5
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+−−
+−
++−
+−
=
001369.0z02122.0
2
z1226.0
3
z201.1
4
z857.1
5
z
05373.0z5233.0
2
z263.8
3
z99.26
4
z77.32
5
z49.13
5
G
0.000625s
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−+
−−−
=
000182.0z0025.0
2
z0714.0
3
z
662.2z324.5
2
z3.21
3
z6.42
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++−
−+−
=
0204.0z1429.0
2
z
3
z
616.1z95.26
2
z94.66
3
z6.42
3
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−+−+
−−−−
=
5e624.1z0001819.0
2
z002499.0
3
z07138.0
4
z
666.1z662.2
2
z326.5
3
z3.21
4
z6.42
4
G
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−++−
−−+−
=
007076.0z005755.0
2
z49.0
3
z429.1
4
z
08823.0z193.9
2
z17.52
3
z2.85
4
z6.42
4
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−+−−+
−+
−−−
−−
=
6e624.1z5e624.1
2
z0001819.0
3
z002499.0
4
z07137.0
5
z
162.1z666.1
2
z659.2
3
z33.5
4
z29.21
5
z6.42
5
G
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+−−
+−
++−
+−
=
001369.0z02122.0
2
z1226.0
3
z201.1
4
z857.1
5
z
1697.0z652.1
2
z09.26
3
z2.85
4
z5.103
5
z6.42
5
G
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
54