NEW TIME-FREQUENCY VOWEL QUANTIZATION ENHANCED

SUBBAND HIERARCHY

Fraihat Salam and Glotin Herv´e

Information and System Sciences Lab - UMR 6168, USTV - B.P. 20 132 - 83 957 La Garde, France

Keywords:

Speech analysis, Quantization, Time-frequency, Allen Temporal Algebra, Automatic Speech Recognition.

Abstract:

Speech dynamics may not well be addressed by the conventional speech processing. We analyse here a new

quantization paradigm for vowel coding. It is based on simple Allen temporal interval algebra applied on

subband voicing levels, yielding to a compressed speech representation of only 21 integers for a speech win-

dow up to 32 ms long. Experiments show that we take advantage of the ranking of the average values of the

voicing interval accross the various subbands. Theses new features are evaluated for vowel recognition (1

hour, 6 vowels) on a referenced multispeaker radio broadcast news used during evaluation campaign ESTER.

We work on the subset of the most frequent french vowels. We get 62% class error rate adding the ranking

information to the Allen’s relations, instead of 70% using Allen relations alone, and 57% the set of the raw 48

ﬂoats. We then discuss on the advantage of using more subbands, and we ﬁnaly propose a strategy to tackle

the combinatorial complexity of Allen relations.

1 INTRODUCTION

Most of acoustic speech analysis systems are based

on short-term spectral features : Mel Frequency Cep-

strum Coefﬁcients (MFCC), PLP, etc... The purpose

of this paper is to present and discuss a novel vowel

representation. We propose here to use med-term

Time Frequency (TF) speech dynamics. It has been

established that phonological perception is a subband

(SB) process (Fletcher, 1922). That has inspired vari-

ous algorithms for robust speech recognition (Glotin,

2001), also linked to the TF voicing level (Glotin

et al., 2001; Glotin, 2001). Nevertheless, the SB

TF dynamics may be more investigated, compared

to usual delta and delta-delta coefﬁcients. Thus we

propose in this paper a quantization of TF dynam-

ics following some preliminary works (Divenyi et al.,

2006; Glotin, 2006). We base our approach on voic-

ing dynamics, composing binary intervals, assuming

that they may provide a qualitative framework to gen-

erate parsimonious phoneme features using the time

events representation proposed by Allen J.F.(Allen,

1981)

In (Fraihat et al., 2008) we made preliminary ex-

Note that ALLEN J.B worked on SB speech analysis, but

ALLEN J.F on generic time representation, while our model is

based on both.

periments yielding to 70% of vowel classiﬁcation.

Here we present a method that signiﬁcantly enhance

the model, adding the subband ranking, and we dis-

cuss on further works. Experiments are conducted

on the most french frequent vowels of one hour of

the ESTER broadcast news database

(Galliano et al.,

2005).

In the ﬁrst section of this paper we recall the Allen

temporal Algebra, and the propertiesof TF voicing in-

dex. Then section 3 shows how we binarize and gen-

erate our speech parsimonious representation. After

a presentation of the vowel coding, we propose dif-

ferent features sets and we show their class error rate

results. We then discuss on the strategy that should be

conducted for developing robust TFQ features.

2 ALLEN TEMPORAL ALGEBRA

A temporal algebra has been deﬁned in (Allen, 1981;

Glotin, 2006), where 14 atomic relations (including

the ’no-relation’ one) are depicted between two time

intervals. These Allen’s time relations are deﬁned by

one interval sliding another. If one set to 1 the a al-

gebraic distance d between the two nearest intervals,

ESTER: Evaluation campaign of continuous speech broadcast

news rich transcription

189

Salam F. and Hervé G. (2008).

NEW TIME-FREQUENCY VOWEL QUANTIZATION ENHANCED BY SUBBAND HIERARCHY.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 189-192

DOI: 10.5220/0001933601890192

 SciTePress

and increment it as the intervals moveaway, we deﬁne

n integer for each relation. Thus the “b” symbol is

coded into “1”, “m” into “2”, ...for the 14 relations

that are : before, meets, overlaps, stars, during, ﬁn-

ishes, equals, and their symmetric (see (Fraihat et al.,

2008) for details). The ’no-relation’ happens between

two empty intervals. We propose to use these time

representation for coding speech events into a small

discrete integer set. In order to deﬁne the intervals we

use the voicing levels as depicted in the next section.

In order to get the subband voicing activity inter-

vals, we estimate the TF voicing activity interval us-

ing the voicing measure R (Glotin, 2001) that is well

correlated with SNR and equivalent to the harmonic-

ity index (HNR). R is calculated by autocorrelogram

of the demodulated signal. In the case of Gaussian

noise, the correlogram of a noisy frame is less modu-

lated than a clean one. We ﬁrst compute the demodu-

lated signal after half wave rectiﬁcation, followed by

pass-band ﬁltering in the pitch domain. Then we au-

tocorrelate each frame of LVW (Local Voicing Win-

dow) ms long and we calculate R = R1/R0, where R1

is the local maximum in time delay segment corre-

sponding to the fundamental frequency ([90 350]Hz),

and R0 is the window energy. We showed (Glotin,

2001) that R is strongly correlated with SNR in the

5..20dB range as illustrated in ﬁg. 1. The SB are

deﬁned as in ALLEN J.B. analysis (Allen, 1994;

Glotin, 2001) : [216 778;707 1631;1262 2709;2121

3800;3400 5400;5000 8000] Hz.

We set for vowel recognition LVW=32ms, with a shift

of 4ms.

3 BINARIZATION AND

REPRESENTATION

In order to generate principal separated time intervals

for Allen relations, we threshold the voicing levels :

for each band and each window of Local Binary Win-

dow (LBW 32ms shift and 64 ms length), we binarize

to 1 the T% frame highest quantil, the other to 0.

In order to remove noisy relation, we remove in-

terval that is connected to any window range. Finally

we keep window containing at least 4 connected in-

tervals. We then derive their Allen temporal relations

(see ﬁg. 1). The vowel labels for the training task

are given from forced realignment on standard HMM-

MMG model (Galliano et al., 2005).

As we have 6 SB, we have 15 temporal relations

(one for each couple), ordered from low to high fre-

quency. In our example (ﬁg. 1), from I’1 to I’5, we

get the parameter vector [di di di oi oi d d d d s oi

d oi f d], where i is the inverse relation. Then these

Figure 1: From voicing levels to the Allen’s interval rela-

ions: (a) voicing signal (b) the voicing level by subband (c)

the binarized voicing levels by subband using mean thresh-

old (From (Glotin, 2001)).

TFQ features estimated in each LBW window, feed a

neural network (any classiﬁer could be used), that we

trained for automatic vowel decoding.

Moreover, in order to conﬁrm that voicing levels

and intervals deﬁnitions are informative, we build a

6 integer feature, called RANK, ranking the subband

of each window using the relative R level of each in-

terval. This information may be correlated to the for-

mant position, that we lose in simple ALLEN rela-

tions.

Thus the functions of binarization and extraction

should also integrate the hierarchy of SB frequency in

ALLEN+RANK concatenated features.

4 DATABASE

Our experiments are made over all the speak-

ers on the six most frequent French vowels:

/Aa/,/Ai/,/An/,/Ei/,/Eu/,/Ii/. SB are deﬁned like in pre-

vious section. We set the shift of each voicing window

LVW to 4ms , and the LVW length to 32ms. We vary

the T% parameter in [0.4 0.5 0.6 0.7]. The training

windows are labelled with the label which covers at

most the window. The features from 1h of continuous

speech are used to train an MLP, and we test on other

20 minutes, best results with number of hidden units

are given in tab.1.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

190

Table 1: Results of the class error rates of the experiments. The error rate of the random classiﬁer is 83%. T is the proportion

of 1 i

n the window in each SB after binarisation. The Relative Gain is the relative reduction of error rate against the voicing

experience. #dim : dimension number of the MLP input. CP: compression ratio of the Parameters. Nhu: Hidden units

numbers of the MLP.

Type of T # Type # CP Nhu Class Error Relative

Features dim bytes Train Test Gain

(%) (%) (%)

Voicing - 48 ﬂoat 384 1 128 49,8 57,2 -

Binairy 0.5 48 bool 48 8 512 75,3 67,5 -18

Allen 0.4 15 int 60 6,4 128 10,1 72,2 -20,7

Allen 0.5 id id id id 512 14,7 70,5 -23,2

Allen 0.6 id id id id 128 10,2 72 -25,8

Allen 0.7 id id id id 128 12,3 70 -23,3

Rank 0.5 6 int 24 16 32 67,4 69 -20,6

Allen+Rank 0.5 15+6 id 84 4,6 512 9,7 62,4 -9,1

Allen+Rank 0.6 id id id id 128 11,7 65,1 -13,8

Allen+Rank 0.7 id id id id 128 4,3 67,7 -18,3

voicing DATA

bands

2 4 6 8

Binary DATA

bands

2 4 6 8

voicing DATA

bands

2 4 6 8

Binary DATA

bands

2 4 6 8

voicing DATA

bands

2 4 6 8

Binary DATA

bands

2 4 6 8

Figure 2: Example of ﬂoat R voicing values

and B

inary data of three different sample of

vowel /Aa/. The vectors of these examples are:

vec1=[d,io,io,no,io,io,io,no,io,if,no,is,no,no,io],

vec2=[io,io,io,no,no,s,id,no,no,id,no,no,id,no,no,no],

vec3=[s,s,d,d,no,s,io,io,d,d,no,is,no,no].

Binary DATA

bands

1 2 3 4 5 6 7 8 9

Binary DATA

bands

1 2 3 4 5 6 7 8 9

Figure 3: Example of voicing and binary data of two differ-

ent s

amples of vowel /Ii/.

5 RESULTS AND DISCUSSION

We notice in the ﬁgure 2 that there is a shape similar-

ity between patterns 1 and 2, and differences between

2 and 3. This may be due to different speakers that

may negatively inﬂuence phoneme recognition (Frai-

hat et al., 2008). Further studies will have to be con-

ducted on this issue.

The concatenation of subband ranks (RANK) and

ALLEN features well improve the score : we have at

best 70% Class Error Rate (ER) at best with ALLEN

features alones, and 62% with ALLEN+RANK fea-

tures (see table 1). Moreover it is interesting to note

that RANK features alone, with 6 integers give 69%

ER, similar to the complementary ALLEN features.

This tends to show that the interval construction algo-

rithm we propose extract representative information

for vowel coding.

These vowel recognition results, with a feature

compression of 4,6 are interesting (=62% ER), com-

pared to the 57% ER given by the raw voicing data

(we note that the direct binarization of the voicing

data is worst) and compared to the 83% ER given by

random classiﬁer (see footnote

Moreover interval soft coding may enhance clas-

siﬁcation as revealed by the results of raw vs binary

voicing levels. We then could use mean and variance

interval length to enhance our classiﬁcation. In fu-

ture works will also use more detailed subband repre-

sentation, like the 36 Mel Filter Cepstral Coefﬁcient.

This multiplication of the number of the intervals may

explose the ALLEN representation size. A simple

way to tackle this combinatorial effect is to generate

local ALLEN relations on some frequency domains,

and to train local classiﬁer for each domain. Then a

The error rate of the random classiﬁer equals 1−

∑

k=1

)

1 −

∑

k=1



card(C

)

∑

k=1

card(C)



, where c is the number of classes,

card(C

) is the number of elements of the class C

in the train set.

NEW TIME-FREQUENCY VOWEL QUANTIZATION ENHANCED BY SUBBAND HIERARCHY

191

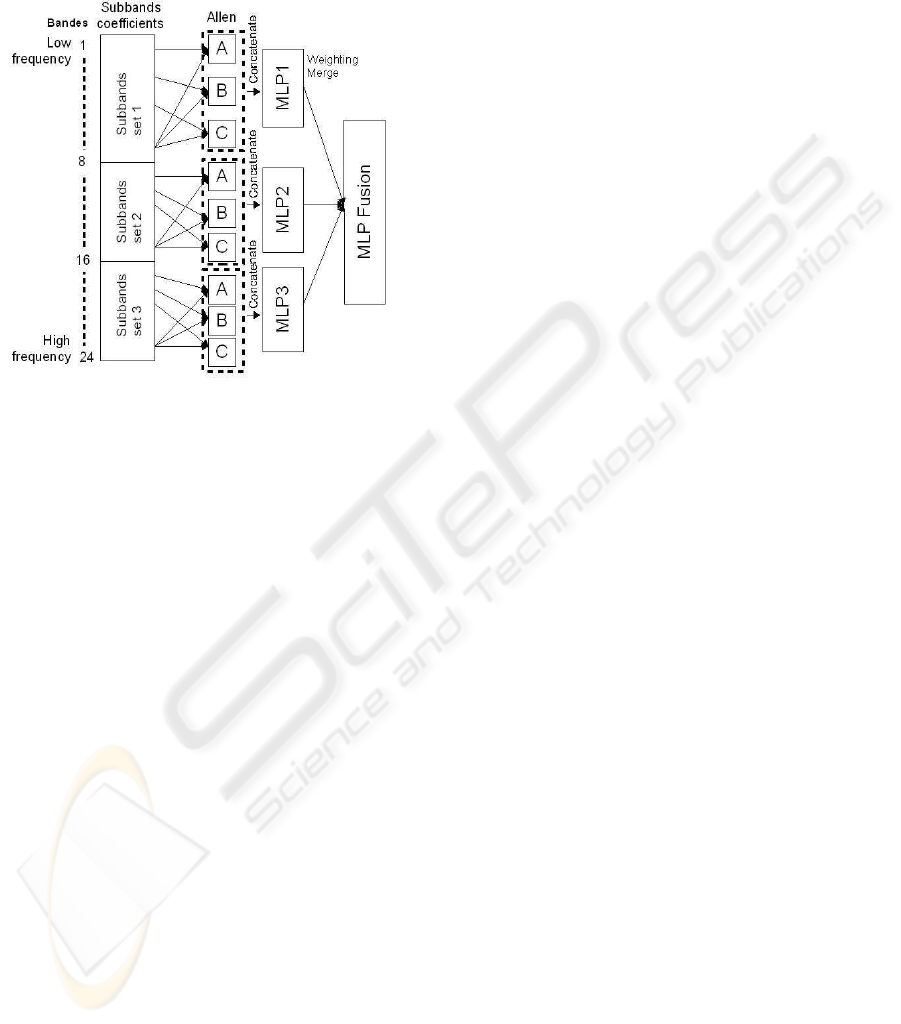
global classiﬁer can merge the whole information, as

epicted in ﬁg 4. This strategy could allow the appli-

cation of method to usual MFCC delta, delta-delta for

example.

Figure 4: Schema of a further system. One may divide the

eatures into three parts and for each part generate three

Allen relations sets from six overlapped subbands, yield-

ing to 3*15 relations that feed a MLP, ﬁnally one merge the

three MLPs.

Further experiments will also be conducted on

consonants, considering for example a zeros inter-

val (ie. between two vowels) or by considering null

binarized intervals (i.e. less or unvoiced intervals).

A simple classic silence detector (e.g. based on en-

ergy thresholding) will avoid confusion between con-

sonant and silence events. Moreover di-phones Con-

sonant Vowel (CV), and triphones sequences (CVC)

modeling could be done with simple extension of the

same framework, and are expected to contribute to en-

hance ASR robustness.

ACKNOWLEDGEMENTS

We thank G.LINARES at LIA and G.GRAVIER at

INRIA for having given the phonetic labels from their

ASR system.

REFERENCES

Allen, J. (1981). An interval-based representation of tem-

poral knowledge. In 7th IJCAI, pages 221–226.

Allen, J. (1994). How do humans process and recognise

speech. In IEEE Trans. on Speech and Signal Pro-

cessing 2(4), pages 567–576.

Divenyi, P., Greenberg, S., and Meyer, G. (2006). Dynamics

of Speech Production and Perception. IOS Press Inc.

Fletcher, H. (1922). The nature of speech and its interpreta-

tion. J. Franklin Inst., 193 6:729–747.

Fraihat, S., Aloui, N., and Glotin, H. (2008). Parsimonious

time-frequency quantization for phoneme and speaker

classiﬁcation. In IEEE Conference on Electrical and

Computer Engineering (CCECE).

Galliano, S., Geoffrois, E., a. M. D., Choukri, K., Bonastre,

J.-F., and Gravier, G. (2005). The ester phase 2 : Eval-

uation campaign for the rich transcription of french

broadcast news. European Conf. on Speech Commu-

nication and Technology, pages 1149–1152,.

Glotin, H. (2001). Elaboration and comparatives studies of

robust adaptive multistream speech recognition using

voicing and localisation cues. In Inst. Nat. Polytech

Grenoble & EPF Lausanne IDIAP.

Glotin, H. (2006). When allen j.b. meets allen j.f.: Quantal

time-frequency dynamics for robust speech features.

Technical report, Research Report LSIS 2006, Lab

Systems and Information Sciences UMR-CNRS.

Glotin, H., Vergyri, D., Neti, C., Potamianos, G., and Luet-

tin, G. (2001). Weighting schemes for audio-visual

fusion in speech recognition. In IEEE int. conf. Acous-

tics Speech & Signal Process. (ICASSP).

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

192