
NOISE REDUCTION BASED ON CROSS TF ε-FILTER
Tomomi Abe
Major in Pure and Applied Physics, Waseda university 55N-4F-10A, 3-4-1 Okubo, Shinjuku-ku, Tokyo, 169-8555, Japan
Mitsuharu Matsumoto, Shuji Hashimoto
Department of Applied Physics, Waseda university 55N-4F-10A, 3-4-1 Okubo, Shinjuku-ku, Tokyo, 169-8555, Japan
Keywords:
Noise reduction, speech enhancement, ε-filter, time-frequency domain.
Abstract:
A time-frequency ε-filter (TF ε-filter) is an advanced ε-filter applied to complex spectra along the time axis. It
can reduce most kinds of noise while preserving a signal that varies frequently such as a speech signal. The
filter design is simple and it can effectively reduce noise. It is applicable not only to small amplitude stationary
noise but also to large amplitude nonstationary noise. However when we consider the noise that varies much
frequently along the time axis, TF ε-filter cannot reduce noise without the signal distortion. When we consider
the noise where the neighboring frequency bins have similar powers such as impulse noise, we can reduce the
noise by using ε-filter applied to the complex spectra not along the time axis, but along the frequency axis.
This paper introduces an advanced method for noise reduction that applies ε-filter to complex spectra not only
along the time axis but also along the frequency axis labeled cross TF ε-filter. We conducted the experiments
utilizing the sounds with stationary, nonstationary and natural noise.
1 INTRODUCTION
Noise reduction plays an important role in speech
recognition and individual identification. When
we consider the instruments like hearing-aids and
phones, noise reduction for a monaural sound is
strongly expected. It will also be easy to miniatur-
ize the system size because it requires only one sig-
nal. The spectral subtraction (SS) is a well-known ap-
proach for reducing the noise signal of the monaural-
sound (Boll, 1979). It can reduce the noise effectively
despite of the simple procedure. However, it can han-
dle only the stationary noise. It also needs to estimate
the noise in advance. Although noise reduction uti-
lizing Kalman filter has also been reported (Kalman,
1960; Fujimoto and Ariki, 2002), the calculation cost
is large. Some authors have reported a model based
approach for noise reduction (Daniel et al., 2006).
In this approach, we can extract the objective sound
by learning the sound model in advance. However,
it is not applicable to the signals with the unknown
noise as well as SS. There are some approaches uti-
lizing comb filter (Lim et al., 1978). In this approach,
we firstly estimate the pitch of the speech signal, and
reduce the noise signal utilizing comb filter. How-
ever, the estimation error results in the degradation
of the speech quality. Some authors have reported
the method utilizing ε-filter (Harashima et al., 1982;
Arakawa et al., 2002). ε-filter is a nonlinear filter,
which can reduce the noise signal with preserving the
signal. ε-filter is simple and has some desirable fea-
tures for noise reduction. It does not need to have the
model not only of the signal but also of the noise in
advance. It is easy to be designed and the calculation
cost is small. It can reduce not only the stationary
noise but also the nonstationary noise. However, it
can reduce only the small amplitude noise in princi-
ple. To solve the problems, the method labeled TF
ε-filter was proposed (Abe et al., 2007). TF ε-filter
is an improved ε-filter applied to the complex spec-
tra along the time axis in time-frequency domain. By
utilizing TF ε-filter, we can reduce not only small am-
plitude stationary noise but also large amplitude non-
stationary noise. However TF ε-filter cannot reduce
the noise without distortion when the noise changes
frequently along the time axis such as impulse noise.
To solve the problem, we apply ε-filter to complex
spectra not only along the time axis but also along the
105
Abe T., Matsumoto M. and Hashimoto S. (2008).
NOISE REDUCTION BASED ON CROSS TF -FILTER.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 105-112
DOI: 10.5220/0001935001050112
Copyright
c
SciTePress

frequency axis labeled cross TF ε-filter. By apply-
ing ε-filter to the complex spectra along the two axes,
we can reduce the noise even if it changes frequently
along the time axis. It need not estimate the noise as
well as TF ε-filter in advance. We also show the ex-
perimental results of the proposed method compared
to the other methods such as SS and TF ε-filter.
2 NOISE REDUCTION
UTILIZING TD ε-FILTER AND
TF ε-FILTER
To clarify the problems of a time-domain ε-filter
(TD ε-filter)(Harashima et al., 1982; Arakawa et al.,
2002), we firstly explain the TD ε-filter algorithm. Let
us define x(k) as the input signal at time k. Let us also
define y(k) as the output signal of the ε-filter at time k
as follows:
y(k) = x(k) +
P
∑
i=−P
a(i)F(x(k+ i) − x(k)), (1)
where a(i) represents the filter coefficient. a(i) is usu-
ally constrained as follows:
P
∑
i=−P
a(i) = 1. (2)
The window size of the ε-filter is 2P+ 1. F(x) is the
nonlinear function described as follows:
|F(x)| ≤ ε
0
: −∞ ≤ x ≤ ∞, (3)
where ε
0
is a constant. This method can reduce small
amplitude noise while preserving the speech signal.
For example, we can set the nonlinear function F(x)
as follows:
F(x) =
x (−ε
0
≤ x ≤ ε
0
)
0 (otherwise).
(4)
Figure 1 shows the basic concept of an ε-filter
when Eq.4 is utilized as F(x). Figure 1(a) shows the
waveform of the input signal.
Executing the ε-filter at point A in Figure 1(a), we
first replace all the points where the distance from A
is larger than ε
0
by the value of point A. We then
summate the signals in the same window. Figure 1(b)
shows the basic concept of this procedure. The dotted
line represents the points where the distance from A
is larger than ε
0
. In Figure 1(b), the continuous line
represents the values replaced through this procedure.
As a result, if the points are far from A, the points are
ignored. On the other hands, if the points are close to
A, the points are smoothed. Due to this procedure, the
ε0
ε0
ε0
ε0
ε0
ε0
ε0
ε0
B
A
(a) Input signal
A
(b) When a TD ε-filter
is applied to the point A
B
Amplitude
Time
(c) When a TD ε-filter
is applied to the point B
Amplitude
Time
Amplitude
Time
Figure 1: The basic concept of a TD ε-filter.
ε-filter reduces noise while preserving the precipitous
attack and decay of the speech signal. In the same
way, by executing the ε-filter at point B in Figure 1(a),
we replace all the points where the distance from B is
larger than ε
0
by the value of the point B. The points
are ignored if they are far from B, while the points
are smoothed if the points are close to B as shown in
Figure 1(c). Consequently, we can reduce small am-
plitude noise near by the processed point while pre-
serving the speech signal.
An ε-filter can reduce small amplitude noise in the
time domain. However, due to the procedure, it is
not applicable to large amplitude noise. To solve this
problem, Time-Frequency ε-filter (TF ε-filter) was
proposed (Abe et al., 2007). TF ε-filter utilizes the
distribution difference of the speech signal and the
noise in the frequency domain. The following as-
sumptions regarding the sound sources are used:
• Assumption 1. Speech signal has greater vari-
ation in power than noise signal in the time-
frequency domain.
• Assumption 2. Noise signal is distributed more
uniformly and with less variation in the time-
frequency domain.
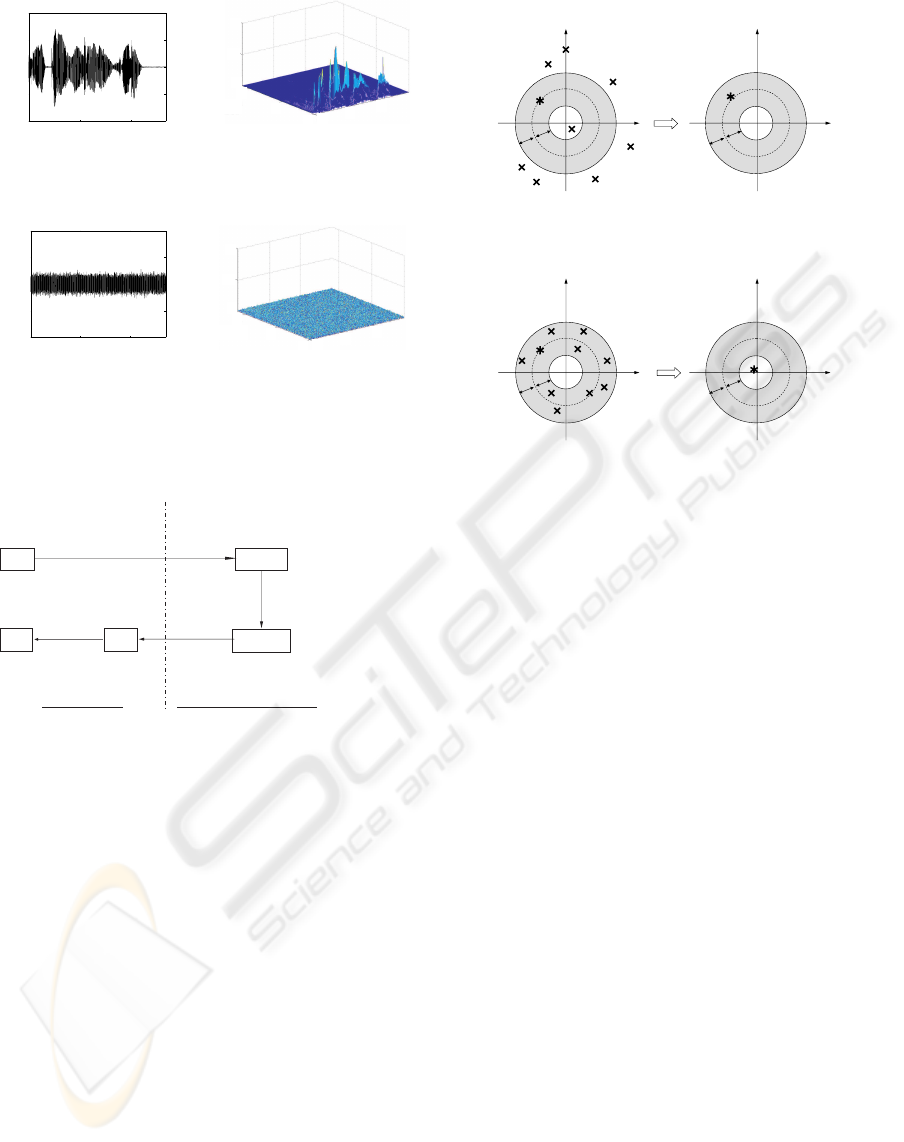
Figure 2 depicts the speech signal and the white noise
signal in the time and the time-frequency domains.
As shown in Figure 2, assumptions 1 and 2 are
fulfilled in the case of various noise like white noise
and natural noise such as the sound of a cooling fan.
In Figures 2(b) and (d), the power is normalized using
the maximal power of the speech signal. When we
consider frequency bins where there are signals, the
ratio of noise power to signal power is smaller than
the ratio of noise amplitude to signal amplitude in the
time domain. In TF ε-filter, we utilize this feature to
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
106
0 1 2
-0.4
-0.2
0
0.2
0.4
Time[s]
Amplitude
(a)
Speech signal
(in time domain)
Time[s]
Power
1
0.5
0
2
1
0
0
1
2
x 10
4
Frequency[Hz]
(b)Speech signal
(in time-frequency domain)
0 1 2
-0.4
-0.2
0
0.2
0.4
Time[s]
Amplitude
(c)
Noise signal
(in time domain)
Power
Frequency[Hz]
Time[s]
1
0.5
0
2
1
0
0
1
2
x 10
4
(d) Noise signal
(in time-frequency domain)
Figure 2: A speech signal or noise signal in the time and
frequency domains.
x(
k
)
STFT
V (
κ
,
ω
)
y(k)
ISTFT
Time domain
Time-frequency domain
(2)
(1)
(4)
TF ε-filter
along the frequency axis
X(
κ
,
ω
)
(3)
v(k)
TD ε-filter
Figure 3: Block diagram of combining TF ε-filter and TD
ε-filter.
apply an ε-filter to high-level noise.
Figure 3 illustrates the method combining TF ε-
filter and TD ε-filter with a block diagram. As shown
in Figure 3(1), we firstly transform the input signal
x(k) to the complex amplitude X(κ, ω) by short term
Fourier transformation(STFT) as follows:
X(κ, ω) =
∞
∑
l=−∞
x(κ+ l)W(l)e
− jωl
, (5)
where W, κ and ω represent the window function, the
time frame in the time-frequency domain and the an-
gular frequency, respectively. j represents the imag-
inary unit. Next we execute a TF ε-filter, which is
an ε-filter applying to complex spectra along the time
axis in the time-frequency domain, as shown in Fig-
ure 3(2). In this procedure, V(κ, ω) is obtained as
follows:
V(κ, ω) =
Q
∑
i=−Q
a(i)X
′
(κ+ i, ω), (6)
Re
Im Im
Re
A
A'
εF
εF
εF
εF
(a) Speech signal
Im
Re
Im
Re
B'
B
εF
εF
εF
εF
(b) Noise signal
Figure 4: Differences in performance when a TF ε-filter is
applied to the speech signal and noise.
where the window size of ε-filter is 2Q+ 1,
X
′
(κ+ i, ω) (7)
=
X(κ, ω)
(||X(κ, ω)| − |X(κ+ i, ω)|| > ε
T
)
X(κ + i, ω)
(||X(κ, ω)| − |X(κ+ i, ω)|| ≤ ε
T
)
and ε
T
is a constant.
Figure 4 illustrates the differences in performance
when we apply a TF ε-filter to the speech signal and
the noise. The horizontal axis and the vertical axis
represent the real axis and the imaginary axis, respec-
tively. In Figure 4, ∗ and × represent the processed
point and the other signal points in the same win-
dow, respectively. Point A in Figure 4(a) and point
B in Figure 4(b) represent the complex amplitude of
the processed point. A
′
and B
′
represent the complex
amplitudes of the outputs when we apply the TF ε-
filter to the points A and B, respectively. Executing
the TF ε-filter, we firstly replace the complex ampli-
tude of the signal outside of the shadow area by that
of A. We then summate the complex spectra of all
the points in the same window. Due to handling com-
plex spectra, when we have many signals that have
similar amplitudes but different phases, the real part
and imaginary part cancel each other. In other words,
even if the amplitude of the noise is large, the noise
is reduced because they cancel each other. Note that
the noise is reduced not only when the amplitude of
NOISE REDUCTION BASED ON CROSS TF e-FILTER
107
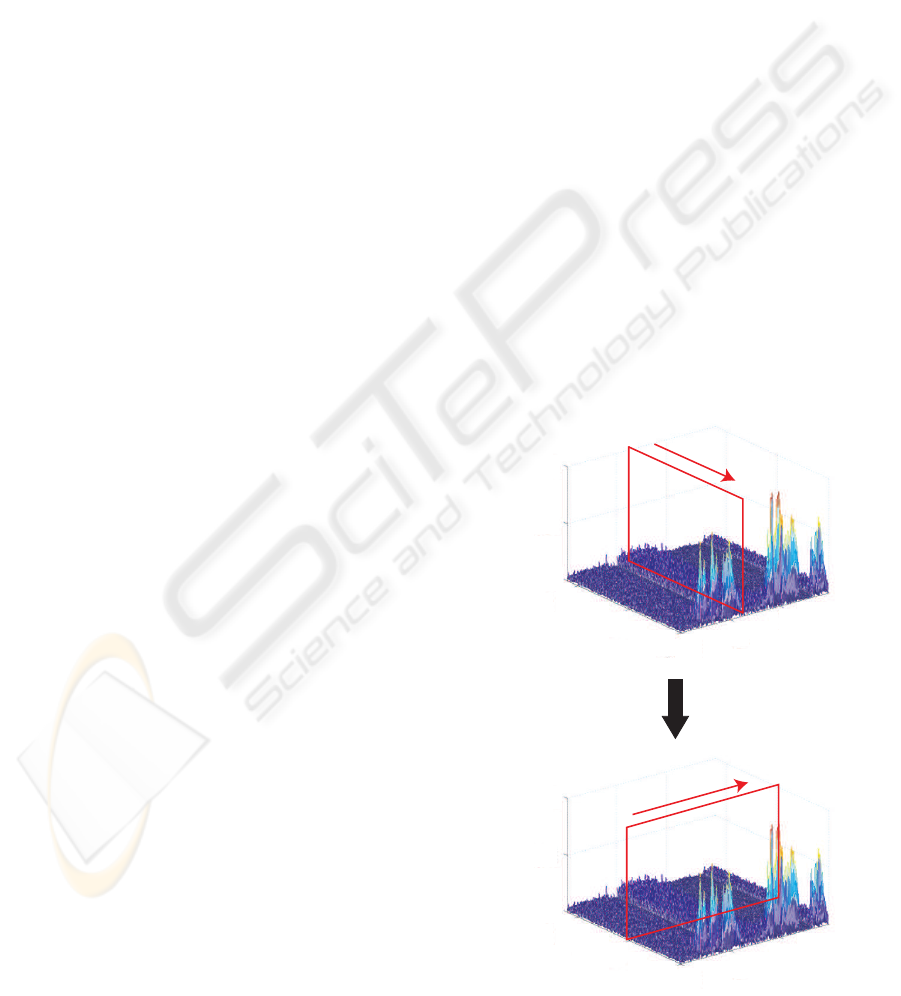
the noise is small but also when the amplitude of the
noise is large because of this procedure. Figure 4(a)
represents the basic concept in the case that the power
varies drastically like a speech signal. When we con-
sider a signal whose power varies frequently, the dif-
ference between the absolute value of A and that of
the other signals is large as shown in Figure 4(a). For
this reason, many signals in the same window as the
point A are replaced by A. As a result, when we han-
dle the speech signal, the complex amplitude of the
processed point is intact. Figure 4(b) represents the
basic concept in case that the power does not vary so
much like a noise signal. When we consider a noise
signal, the difference between the absolute value of B
and that of the other signals is relatively small com-
pared with the speech signal. Hence, few signals in
the same window as point B are replaced by B. In
other words, when handling noise, the complex am-
plitude of the processed point becomes smaller when
the TF ε-filter is applied. Based on these aspects, we
can reduce noise while preserving the signal by set-
ting ε
T
appropriately.
Hence, the TF ε-filter is effective even when the
power of the noise to signal is large. Additionally,
under assumption 2, the TF ε-filter becomes more ef-
fective. When assumption 2 is satisfied, the variation
of the noise to the signal in the frequency domain be-
comes smaller than that in the time domain. As a con-
sequence, even if the noise varies frequently in the
time domain, the ε-filter can be applied in the time-
frequency domain.
Next, we transform V(κ, ω) to v(k) by inverse
STFT as shown in Figure 3(3).
To reduce the remaining noise, we additionally ap-
ply the ε-filter in the time domain to v(k) as shown in
Figure 3(4). Note that the ε-filter in the time domain
can be utilized because large amplitude noise has al-
ready been reduced in the previous procedure. The
output y(k) can be obtained as follows:
y(k) =
P
∑
i=−P
a(i)v
′
(k+ i), (8)
where
v
′
(k+ i) =
v(k) (|v(k + i) − v(k)| > ε
t
)
v(k+ i) (|v(k+ i) − v(k)| ≤ ε
t
)
(9)
and ε
t
is a constant.
3 NOISE REDUCTION
UTILIZING CROSS TF
ε-FILTER
TF ε-filter can reduce the various types of noise ef-
fectively. However, when we use the noise that varies
much frequently along the time axis, TF ε-filter can-
not reduce noise without the signal distortion. When
we consider the noise where the neighboring fre-
quency bins have similar powers such as impulse
noise, we can reduce the noise by using ε-filter ap-
plying to complex spectra not along the time axis, but
along the frequency axis.
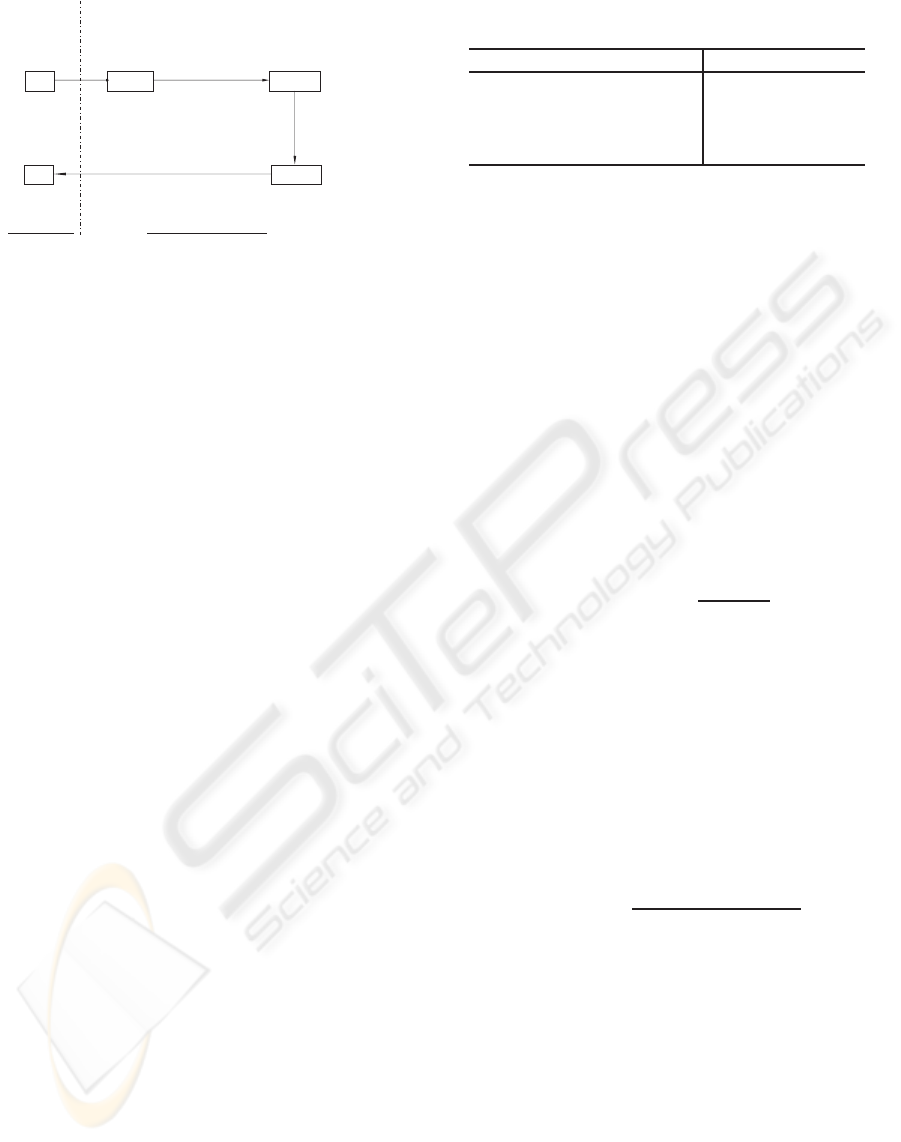
Figure 5 shows the basic concept of the proposed
method. At first, as shown in Figure 5 “Step 1”, we
apply the ε-filter to the complex spectra along the fre-
quency axis to reduce the noise where the neighboring
frequency bins have similar power although the noise
amplitude varies drastically such as the impulse noise
and white noise whose amplitude varies. Next we ap-
ply ε-filter to complex spectra along the time axis to
reduce the noise that distributes wider than the speech
signal in the frequency domain as shown in Figure 5
“Step 2”.
Figure 6 illustrates the proposed method with a
filtering
Frequency[Hz]
Time[s]
filtering
Frequency[Hz]
Time[s]
<Step 1>
<Step 2>
1
0.5
0
2
1
0
0
1
2
x 10
1
0.5
0
2
1
0
0
1
2
x 10
Figure 5: The basic concept of cross TF ε-filter.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
108
x(
k
)
STFT
U (
κ
,
ω
)
y(k
)
ISTFT
Time domain Time-frequency domain
Y(
κ
,
ω
)
(2)
(1)
(4)
ε-filter applying
to complex spectra
along the frequency axis
X(
κ
,
ω
)
ε-filter applying
to complex spectra
along the time axis
(3)
Figure 6: The block diagram of the proposed method.
block diagram. Let us consider x(k), and X(κ, ω)
transformed from x(k) by STFT as well as Eq.5 as
shown in Figure 6(1). Next we apply ε-filter to com-
plex spectra along the frequency axis as shown in Fig-
ure 6(2). In this procedure, U(κ, ω) is obtained as fol-
lows:
U(κ, ω) =
N
∑
i=−N
a(i)X
′
(κ+ i, ω), (10)
where
X
′
(κ+ i, ω) (11)
=
X(κ, ω)
(||X(κ, ω)| − |X(κ, ω+ i)|| > ε
F
)
X(κ, ω + i)
(||X(κ, ω)| − |X(κ, ω+ i)|| ≤ ε
F
).
ε
F
is a constant and 2N + 1 is window size. Then we
employ ε-filter applying to complex spectra along the
time axis as shown in Figure 6(3). In this procedure,
Y(κ, ω) is obtained as follows:
Y(κ, ω) =
M
∑
i=−M
a(i)U
′
(κ+ i, ω), (12)
where
U
′
(κ+ i, ω) (13)
=
U(κ, ω)
(||X(κ, ω)| − |X(κ+ i, ω)|| > ε
T
)
U(κ + i, ω)
(||X(κ, ω)| − |X(κ+ i, ω)|| ≤ ε
T
).
ε
T
is a constant and 2M + 1 is the window size. Next
we transform Y(κ, ω) to y(k) by inverse STFT as
shown in Figure 6(4). We label this process “cross
TF ε-filter”.
4 EXPERIMENT
4.1 Experimental Condition
We conducted the experiments utilizing a speech sig-
nal with a noise signal. As the speech signal, we uti-
Table 1: Common parameters.
Parameter Value
Sampling frequency 44100
STFT Block size
512
Hop size 256
Window function
Hanning window
lized “Japanese Newspaper Article Sentences” edited
by the Acoustical Society of Japan. We also prepared
three kinds of noise signals: stationary noise, nonsta-
tionary noise and natural noise. The signal and the
noise are mixed in the computer. To compare the ef-
fectiveness of the proposed method to other methods,
we conducted the experiments utilizing three meth-
ods; spectral subtraction (SS), the method combining
TF ε-filter and TD ε-filter and cross TF ε-filter. Table
1 shows the value of common parameters for all the
experiments.
To evaluate the performance of noise reduction,
we use signal-to-noise ratio (SNR) and signal-to-
distortion ratio (SDR). SNR is defined as follows:
SNR = 10· log
10
L
∑
k=1
s(k)
2
L
∑
k=1
n(k)
2
, (14)
where s(k), n(k) and L represent the speech signal at
time k, the noise signal at time k, and the length of the
signal, respectively. To calculate SNR of the output
signal, we separately applied each method to the sig-
nal and noise, and calculated the output SNR by using
the obtained signal and noise. SDR can be represented
as follows:
SDR = 10 · log
10
L
∑
k=1
s
in
(k)
2
L
∑
k=1
(s
in
(k) − s
out
(k))
2
, (15)
where s
in
(k) and s
out
(k) represent the input signal and
the output signal at time k respectively, when we used
only the speech signal. SDR represents how much the
signal is distorted by reducing the noise. Through-
out all the experiments, the parameters of SS and the
method combining TF ε-filter and TD ε-filter are set
optimally. On the other hand, in cross TF ε-filter, ε
T
was set at 0.1. We only change ε
F
depending on the
noise to show the robustness concerning the param-
eter setting although we can reduce the noise more
effectively. SNR of the input signal is set at 10[dB]
throughout all of the experiments.
NOISE REDUCTION BASED ON CROSS TF e-FILTER
109
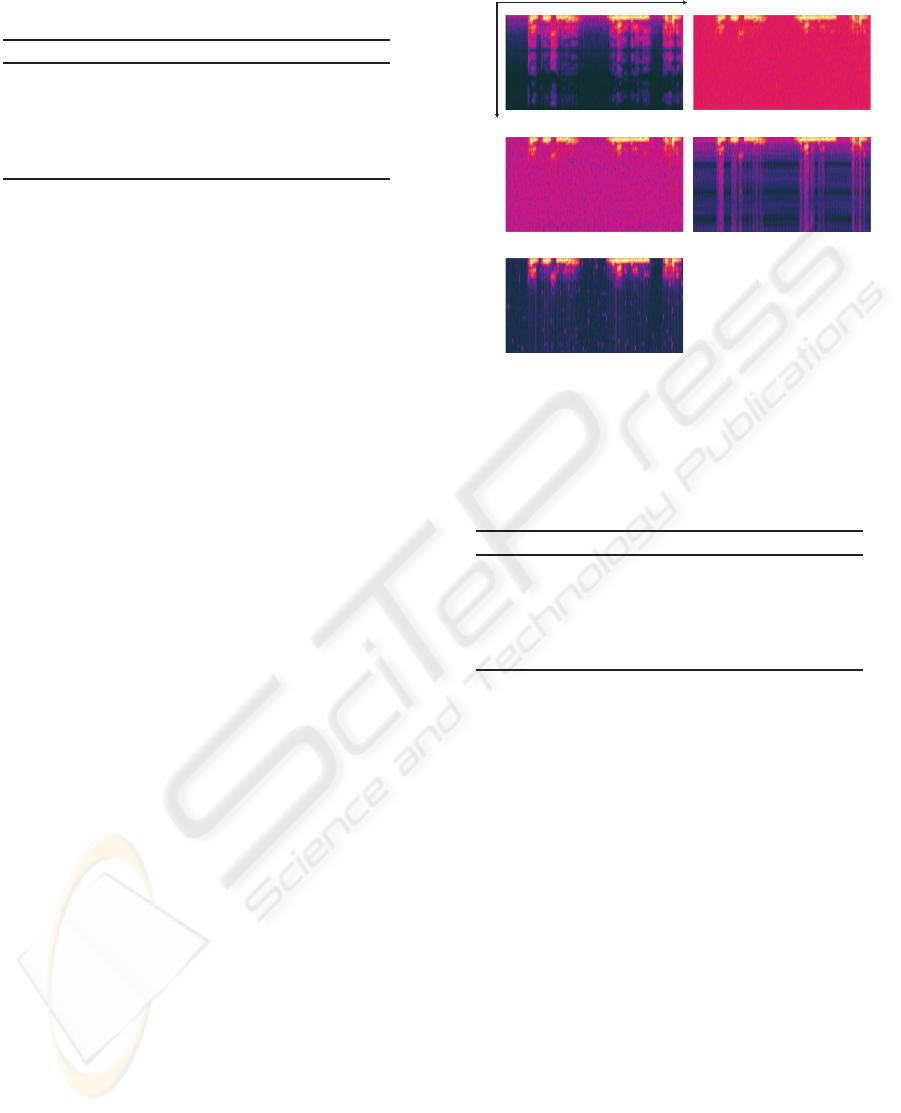
Table 2: SNR and SDR when a signal with stationary noise
is utilized.
SNR[dB] SDR[dB]
Input signal 10.0 —
SS 18.3 21.7
TD ε-filter processed
after TF ε-filter 40.6 18.9
Cross TF ε-filter 44.4 19.3
4.2 Experimental Results in the Case of
Stationary Noise
We first conducted the experiment utilizing a signal
with stationary noise. We prepared a speech signal
and white noise as the signal and the stationary noise,
respectively. We set ε
F
in the proposed method at
0.7. We also set the window size of ε-filter applied to
complex spectra in the proposed method along the fre-
quency axis and the time axis at 101 and 11, respec-
tively. Table 2 shows the results of the experiments
for stationary noise.
As shown in Table 2, the proposed method could
reduce the noise compared to the other methods with
preserving the signal. Figure 7 shows the sound spec-
trograms. In Figure 7, bright color represents that the
signal power is high while dark color represents that
the signal power is low. Figure 7(a) shows the spec-
trogram of the original signal. Figure 7(b) shows the
spectrogram of the signal with stationary noise. Fig-
ures 7(c)-(e) show the spectrograms of the output of
SS, the output of the method combining TF ε-filter
and TD ε-filter and the output of the proposed method,
respectively. As shown in Figure 7, when we used the
proposed method, the noise could be reduced more
effectively than the other methods.
4.3 Experimental Results in the Case of
Nonstationary Noise
The experiment was conducted using a signal with
nonstationary noise. We used the same speech sig-
nal as in Sec.4.2. We prepared white noise with an
amplitude that sometimes varied. We set ε
F
in the
proposed method at 1.1. We also set the window size
of ε-filter applied to complex spectra in the proposed
method along the frequency axis and the time axis
81 and 11, respectively. Table 3 shows the results of
the experiments on nonstationary noise. As shown
in Table 3, the SNR of the proposed method is supe-
rior to those of the other methods. Figure 8(a) shows
the spectrogram of the original signal. Figure 8(b)
shows the spectrogram of the signal with nonstation-
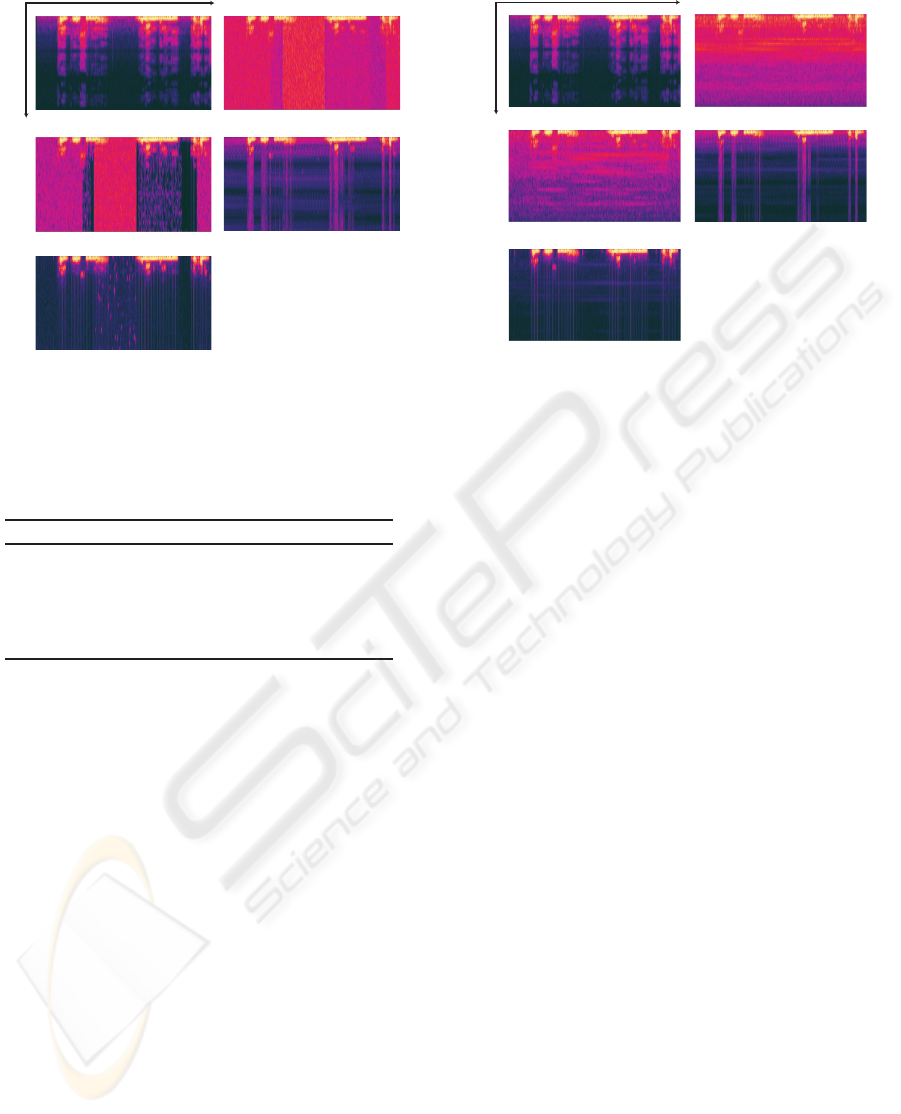
(a) Original signal (b) Input signal
(e) Cross TF ε-filter
(c) Spectral subtraction
Time
Frequency
(d) TF and TD ε-filter
Figure 7: Experimental results when a signal with station-
ary noise is utilized.
Table 3: SNR and SDR when a signal with nonstationary
noise is utilized.
SNR[dB] SDR[dB]
Input signal 10.0 —
SS 15.5 21.9
TD ε-filter processed
after TF ε-filter 40.8 16.3
Cross TF ε-filter 44.2 17.3
ary noise. Figures 8(c)-(e) show the spectrograms of
the outputs of SS, the output of the method combining
TF ε-filter and TD ε-filter and the output of the pro-
posed method, respectively. The relation between the
color and signal power is the same as in Sec.4.2. As
shown in Figure 8, when we use the proposed method,
the noise could be reduced more effectively than the
other methods even if we use the nonstationary noise
as noise.
4.4 Experimental Results in the Case of
Natural Noise
To evaluate the performance of the proposed method
for natural noise, we conducted the experiment uti-
lizing a speech signal and a noise generated from
the cooling fan of a personal computer. The most
power of noise used in this experiment is distributed
in the low-frequency range. We set ε
F
in the proposed
method at 1.8. We also set the window size of ε-filter
applied to complex spectra in the proposed method
along the frequency axis and the time axis 51 and 11,
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
110
(a) Original signal (b) Input signal
(e) Cross TF ε-filter
(c) Spectral subtraction
Time
Frequency
(d) TF and TD ε-filter
Figure 8: Experimental results when a signal with nonsta-
tionary noise is utilized.
Table 4: SNR and SDR when a signal with natural noise is
utilized.
SNR[dB] SDR[dB]
Input signal 10.0 —
SS 17.4 20.1
TD ε-filter processed
after TF ε-filter 38.2 13.4
Cross TF ε-filter 40.2 15.0
respectively. Table 4 shows the results of the experi-
ments for natural noise. As shown in Table 4, the SNR
of the proposed method is superior to those of the
other methods as well as in the case of stationary noise
and nonstationary noise. Figure 9(a) shows the spec-
trogram of the original signal. Figure 9(b) shows the
spectrogram of the signal with natural noise. Figures
9(c)-(e) show the spectrograms of the outputs of SS,
the output of the method combining TF ε-filter and
TD ε-filter and the output of the proposed method, re-
spectively. The relation between the color and signal
power is the same as in Sec.4.2. As shown in Figure
9, when we use the proposed method, the noise could
be reduced more effectively than the other methods
even if the natural noise was used as noise.
5 CONCLUSIONS
In this paper, we introduced an algorithm for noise re-
duction applying ε-filter to complex spectra not only
along the time axis but also along the frequency axis
in time-frequency domain. The proposed method can
(a) Original signal (b) Input signal
(e) Cross TF ε-filter
(c) Spectral subtraction
Time
Frequency
(d) TF and TD ε-filter
Figure 9: Experimental results when a signal with natural
noise is utilized.
reduce not only stationary noise but also nonstation-
ary and natural noise effectively with preserving sig-
nal clarity. The experimental results showed that the
proposed method could be applied to various kinds of
noise. The proposed method could reduce the louder
noise compared with the conventional methods such
as the method combining TF and TD ε-filter and SS.
It is considered that the proposed method can be ap-
plied not only to the speech in Japanese but also to
the speech in English with noise because the perfor-
mance of the proposed method depends on only the
power change of speech and noise signal. For future
works, we would like to confirm the robustness of the
proposed method for various input SNR and various
types of noise. We also aim to determine each param-
eter adaptively.
ACKNOWLEDGEMENTS
This research was supported by the research grant
of Support Center for Advanced Telecommunica-
tions Technology Research (SCAT), by the research
grant of Tateisi Science and Technology Founda-
tion, and by the Ministry of Education, Science,
Sports and Culture, Grant-in-Aid for Young Scien-
tists (B), 20700168, 2008. This research was also
supported by Waseda University Grant for Special
Research Projects(B), No.2007B-142, No.2007B-143
and No.2007B-168, by ”Establishment of Consoli-
dated Research Institute for Advanced Science and
Medical Care”, Encouraging Development Strategic
Research Centers Program, the Special Coordina-
NOISE REDUCTION BASED ON CROSS TF e-FILTER
111

tion Funds for Promoting Science and Technology,
Ministry of Education, Culture, Sports, Science and
Technology, Japan, by the CREST project ”Founda-
tion of technology supporting the creation of digi-
tal media contents” of JST, by the Grant-in-Aid for
the WABOT-HOUSE Project by Gifu Prefecture, the
21st Century Center of Excellence Program, ”The in-
novative research on symbiosis technologies for hu-
man and robots in the elderly dominated society”,
Waseda University and by Project for Strategic Devel-
opment of Advanced Robotics Elemental Technolo-
gies (NEDO: 06002090).
REFERENCES
Abe, T., Matsumoto, M., and Hashimoto, S. (2007). A
method of noise reduction for speech signals using
component separating ε-filters. In J. of the Acoustic-
Society America., volume 122, pages 2697–2705.
Arakawa, K., Matsuura, K., Watabe, H., and Arakawa, Y.
(2002). Noise reduction combining time-domain ε-
filter and time-frequency ε-filter. In IEICE trans on
Fundamentals., volume J85-A, pages 1059–1069.
Boll, S. F. (1979). Suppression of acoustic noise in speech
using spectral subtraction. In IEEE Trans. Acoust.
Speech Signal Process., volume ASSP-27, pages 113–
120.
Daniel, P., Ellis, W., and Weiss., R. (2006). Model-based
monaural source separation using a vector-quantized
phase-vocoder representation. In Proc. IEEE Int’l
Conf. on Acoustics, Speech, and Signal Process. 2006.
Fujimoto, M. and Ariki, Y. (2002). Speech recognition un-
der noisy environments using speech signal estimation
method based on kalman filter. In IEICE Trans. Infor-
mation and Systems, volume J85-D-II, pages 1–11.
Harashima, H., Odajima, K., Shishikui, Y., and Miyakawa,
H. (1982). ε-separating nonlinear digital filter and its
applications. In IEICE trans on Fundamentals., vol-
ume J65-A, pages 297–303.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. In Trans. of the ASME, vol-
ume 82, pages 35–45.
Lim, J. S., Oppenheim, A. V., and Braida, L. (1978). Eval-
uation of an adaptive comb filtering method for en-
hancing speech degraded by white noise addition. In
IEEE Trans. on Acoust. Speech Signal Process., vol-
ume ASSP-26, pages 419–423.
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
112
