SUFFIX ARRAYS

A Competitive Choice for Fast Lempel-Ziv Compressions

Artur J. Ferreira

1,3

, Arlindo L. Oliveira

2,4

and M´ario A. T. Figueiredo

3,4

Instituto Superior de Engenharia de Lisboa, Lisboa, Portugal

Instituto de Engenharia de Sistemas e Computadores: Investigac¸˜ao e Desenvolvimento, Lisboa, Portugal

Instituto de Telecomunicac¸ ˜oes, Lisboa, Portugal

Instituto Superior T´ecnico, Lisboa, Portugal

Keywords:

Lempel-Ziv, Lossless Data Compression, Sufﬁx Arrays, Sufﬁx Trees, String Matching.

Abstract:

Lossless compression algorithms of the Lempel-Ziv (LZ) family are widely used in a variety of applications.

The LZ encoder and decoder exhibit a high asymmetry, regarding time and memory requirements, with the

former being much more demanding. Several techniques have been used to speed up the encoding process;

among them is the use of sufﬁx trees. In this paper, we explore the use of a simple data structure, named

sufﬁx array, to hold the dictionary of the LZ encoder, and propose an algorithm to search the dictionary.

A comparison with the sufﬁx tree based LZ encoder is carried out, showing that the compression ratios are

roughly the same. The ammount of memory required by the sufﬁx array is ﬁxed, being much lower than the

variable memory requirements of the sufﬁx tree encoder, which depends on the text to encode. We conclude

that sufﬁx arrays are a very interesting option regarding the tradeoff between time, memory, and compression

ratio, when compared with sufﬁx trees, that make them preferable in some compression scenarios.

1 INTRODUCTION

Lossless compression algorithms of the Lempel-Ziv

(LZ) family (Salomon, 2007; Ziv and Lempel, 1977;

Storer and Szymanski, 1982) are widely used in a va-

riety of applications. These coding techniques exhibit

a high asymmetry in terms of the time and memory

requirements of the encoding and decoding processes,

with the former being much more demanding due to

the need to build, store, and search over a dictionary.

Considerable research efforts have been devoted to

speeding up LZ encoding procedures. In particular,

efﬁcient data structures have been suggested for this

purpose; in this context, sufﬁx trees (ST) (Gusﬁeld,

1997; Ukkonen, 1995; McCreight, 1976; Weiner,

1973) have been proposed in (Larsson, 1996; Lars-

son, 1999).

Recently, attention has been drawn to sufﬁx ar-

rays (SA), due to their simplicity and space efﬁciency.

This class of data structures has been used in such

diverse areas as search, indexing, plagiarism detec-

tion, information retrieval, biological sequence anal-

ysis, and linguistic analysis (Sadakane, 2000). In

data compression, SA have been used to encode data

with anti-dictionaries (Fiala and Holub, 2008) and

optimized for large alphabets (Sestak et al., 2008).

Linear-time SA construction algorithms have been

proposed (Karkainen et al., 2006; Zhang and Nong,

2008). The space requirement problem of the ST has

been addressed by replacing an ST-based algorithm

with another based on an enhanced SA (Abouelhoda

et al., 2004).

In this work, we show how an SA (Gusﬁeld, 1997;

Manber and Myers, 1993) can replace an ST to hold

the dictionary in the LZ77 (also named LZ1) encod-

ing algorithm. We also compare the use of ST versus

SA, regarding time and memory requirements of the

data structures of the encoder.

The rest of the paper is organized as follows. Sec-

tion 2 describes the Lempel-Ziv 77 (Ziv and Lempel,

1977) algorithm and its variant LZSS (Storer and Szy-

manski, 1982). Sections 3 and 4 present the main fea-

tures of ST and SA, showing how to apply them to

LZ77 compression. Some implementation details are

discussed in Section 5. Experimental results are re-

ported in Section 6, while Section 7 presents some

concluding remarks.

J. Ferreira A., L. Oliveira A. and A. T. Figueiredo M. (2008).

SUFFIX ARRAYS - A Competitive Choice for Fast Lempel-Ziv Compressions.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 5-12

DOI: 10.5220/0001935200050012

 SciTePress

2 LZ77 COMPRESSION

2.1 Encoding

A key feature of the Lempel-Ziv 77 (LZ77) encoding

algorithm is the use of a sliding window over the se-

quence of symbols (Salomon, 2007; Ziv and Lempel,

1977). This sliding window is composed of two sub-

windows: the dictionary and the look-ahead-buffer

(LAB). The dictionary holds the characters already

encoded, while the LAB contains the characters still

to be encoded. As a string of characters in the LAB

in encoded, the window slides to include it in the dic-

tionary (the string is said to slide in); consequently,

characters at the far end of the dictionary are dropped

by this sliding procedure (they slide out).

At each step of the LZ77 encoding algorithm, the

longest preﬁx of the LAB which can be found any-

where in the dictionary is determined and its position

is stored. In the example of Figure 1, we ﬁnd the

string of the ﬁrst four symbols of the LAB (“brow”) in

position 17 in the dictionary. The encoding consists in

describing this string followed by the next symbol, by

an LZ77 token, which composed of three ﬁelds (posi-

tion, length, symbol), with the following meanings:

• position - location of the longest preﬁx of the

LAB found in the current dictionary; this ﬁeld

uses log

(|dictionary|) bits, where |dictionary| is

the length of the dictionary;

• length - length of the matched substring; this re-

quires log

(|LAB|) bits.

• symbol - the ﬁrst character, in the LAB, that does

not belong to the matched substring (the character

that breaks the match); for ASCII symbols, this

uses 8 bits.

In the example of Figure 1, the string “brows” is en-

coded by (17,4,s). Since a sequence of 5 symbols

was encoded, the window slides 5 positions forward,

thus the substring “after” performs a slide out, while

the encoded string “brows” performs a slide in. This

LZ77 token uses log

(|dictionary|)+log

(|LAB|)+8

bits, with (usually) |dictionary| ≫ |LAB|. In the ab-

sence of a match, the LZ77 token is (0,0,symbol). It’s

clear that the key component of the LZ77 encoding

algorithm is a search for the longest match between

preﬁxes of the LAB and the dictionary.

2.2 Decoding

The decoding process is much simpler since it in-

volves no searches. Assuming that it has been assured

that the LZ77 decoder and encoder start with the same

Figure 1: LZ77 encoding: dictionary and LAB, encoding

string “brows”, with the token (17,4,‘s’).

dictionary contents, the decoding procedure is as fol-

lows: for each LZ77 token (position,length,symbol),

the decoder

1. copies “length” symbols, starting at position “po-

sition” of the dictionary, to its output;

2. appends the symbol “symbol” to its output;

3. slides the dictionary forward so that it includes the

string just produced at its output.

Clearly, LZ77 is a very simple procedure, with very

low complexity.

2.3 LZSS Algorithm

An optimized version of LZ77, named Lempel-Ziv-

Storer-Szymanski (LZSS), was proposed in (Storer

and Szymanski, 1982). The three ﬁeld token is mod-

iﬁed to the format (bit,code); the structure of “code”

depend on value “bit” as follows:



bit = 0 ⇒ code = (character),

bit = 1 ⇒ code = (position, length).

(1)

The key idea is that, when there is a non-empty

match, there is no need to encode explicitly the fol-

lowing symbol. LZSS widely used in commercial al-

gorithms, since it typically achieves higher compres-

sion ratios than the original LZ77 algorithm. Well-

known programs such as GZIP and PKZIP are based

on LZSS. The decoding procedure for LZSS is simi-

lar to that of LZ77. Besides the modiﬁcation of the

token, Storer e Szymanski (Storer and Szymanski,

1982) also proposed to keep the LAB in a circular

queue and the dictionary in a binary search tree.

3 SUFFIX TREES FOR LZ77

COMPRESSION

3.1 Sufﬁx Trees

A sufﬁx tree (ST) is a data structure, built from a

string, that contains the entire set of sufﬁxes of that

string (Gusﬁeld, 1997; Ukkonen, 1995; McCreight,

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

1976; Weiner, 1973). Given a string D of length m,

a ST consists of a direct tree with m leaves, num-

bered from 1 to m. Each internal node, except from

the root node, has two or more descendants, and each

branch corresponds to a non-empty substring of D.

The branches stemming from the same node start with

different characters. For each leaf node, i, the con-

catenation of the strings over the branches, starting

from the root to the leaf node i, yields the sufﬁx of D

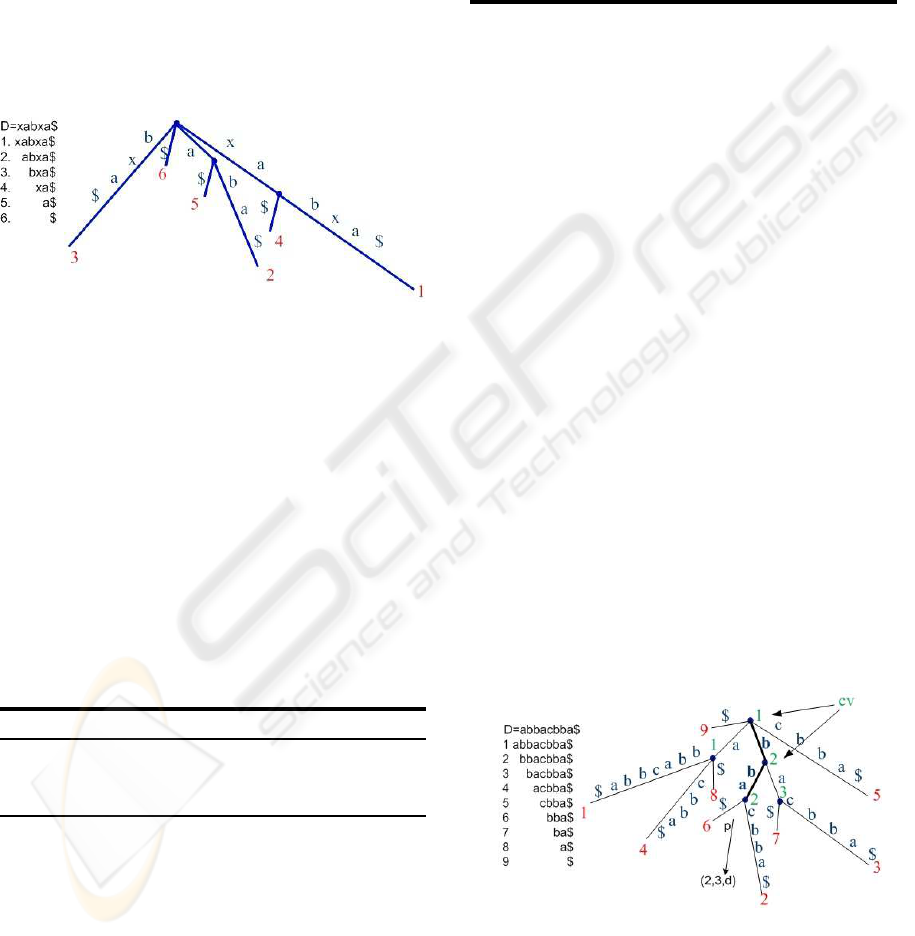
that starts at position i, that is, D[i. . . m]. Figure 2

shows the ST for string D = xabxa$, with sufﬁxes

xabxa$

abxa$

bxa$

xa$

and

. Each leaf node

contains the corresponding sufﬁx number. In order

Figure 2: Sufﬁx Tree for string D = xabxa$. Each leaf node

contains the corresponding sufﬁx number. Each sufﬁx is

obtained by walking down the tree, from the root node.

to be possible to build an ST from a given string, it

is necessary that no sufﬁx of smaller length preﬁxes

another sufﬁx of greater length. This condition is as-

sured by the insertion of a terminator symbol ($) at the

end of the string. The terminator is a special symbol

that does not occur previously on the string.

3.2 Encoding using Sufﬁx Trees

An ST can be applied to obtain the LZ77/LZSS de-

scription of a string, as we describe in Algorithm 1

(Gusﬁeld, 1997).

Algorithm 1: ST-Based LZ77 Encoding.

Inputs: D, dictionary with length |D| = m.

S, string to encode, with length |S| = n.

Output: LZ77 description of S on D.

1. Build, in O (m) time, an ST for string D;

2. Number each internal node v with c

, the smallest

number of all the sufﬁxes in v’s subtree; this way,

is the left-most position in D of any copy of the

substring on the path from the root to node v;

3. To obtain the description (position, length) for the

substring S[i. . . n], with 0 ≤ i ≤ n:

a) Follow the only path from the root that matches

the preﬁx S[i. . . n];

b) The traversal stops at point p (not necessarily

a node), when a character breaks the match; let

depth(p) be the length of the string from the

root to p and v the ﬁrst node at or below p;

c) Do position ← c

and length ← depth(p);

d) Output token (position, length, S[ j]), with j =

i+ length;

e) Do i ← j+ 1; if i = n stop; else goto 3.

The search in step 3b) of the algorithm obtains the

longest preﬁx of S[i. . . n] that also occurs in D. Fig-

ure 3 shows the use of this algorithm for the dictio-

nary D = abbacbba$; every leaf node has the number

of the corresponding sufﬁx while the internal nodes

contain the corresponding c

value. In a similar man-

ner, the algorithm can be applied for LZSS compres-

sion, by modiﬁng step 3d) in order to deﬁne the token,

according to (1). Regarding Figure 3, suppose that we

want to encode the string S = bbad; we traverse the

tree from the root to point p (with depth 3) and the

closest node at or below p has c

= 2, so the token

has position=2 and length=3. The token for S on D is

(2,3,‘d’).

4 SUFFIX ARRAYS FOR LZ77

COMPRESSION

4.1 Sufﬁx Arrays

A sufﬁx array (SA) is the lexicographically sorted ar-

ray of the sufﬁxes of a string, holding the same infor-

mation as the ST, in an implicit way (Gusﬁeld, 1997;

Manber and Myers, 1993). SA is an alternative to

the use of ST, in the sense that it requires (much)

Figure 3: Use of a Sufﬁx Tree for LZ77 encoding, with dic-

tionary D = abbacbba$. Each leaf node contains the corre-

sponding sufﬁx number, while the internal nodes keep the

smallest sufﬁx number on their subtree (c

). Point p shows

the end of the path that we follow, to encode the string

S = bbad.

SUFFIX ARRAYS - A Competitive Choice for Fast Lempel-Ziv Compressions

less memory and has the following features (Gusﬁeld,

1997):

• an SA uses (typically 3 ∼ 5 times) less memory

than an ST for the same string;

• an SA can be used to solve the substring problem

almost as efﬁciently as an ST;

• the use of an SA is more appropriate when the

alphabet of the string has high dimension.

It is possible to convert an ST into an SA in linear

time (Gusﬁeld, 1997). An SA can also be built using a

sorting algorithm, such as “quicksort” and can be ap-

plied to obtain every occurrence of a substring within

a given string. Searching for every occurrence of a

substring consists of ﬁnding every sufﬁx that starts

with the same character as the substring.

Let us consider the string D of length m (with m

sufﬁxes). An SA P is a list of integers from 1 to m,

according to the lexicographic order of the sufﬁxes of

S. For D = mississippi (with m = 11), the sufﬁxes are

mississippi

ississippi

ssissippi

sissippi

issippi

ssippi

sippi

ippi

ppi

10.

11.

After lexicographic sorting, the result is

11.

ippi

issippi

ississippi

mississippi

10.

ppi

sippi

sissippi

ssippi

ssissippi

Thus, the SA that represents D is P =

{11, 8, 5, 2, 1, 10, 9, 7, 4, 6, 3}. Each of these in-

tegers is the sufﬁx number and corresponds to its

position in D. Finding a substring of D can be

done by searching vector P; for instance, the set of

substrings of D that start with character i, can be

found at positions 11, 8, 5 and 2. This way, for LZ77

and LZSS encoding, we can ﬁnd every substring that

starts with a given character.

The lexicographic order of the sufﬁxes implies

that sufﬁxesthat start with the same character are con-

secutive on SA P. This means that a binary search on

P can be used to ﬁnd all these sufﬁxes. This search

takes O (nlog(m)) time, with n being the length of the

substring to ﬁnd, while m is the length of the dic-

tionary. To avoid some redundant comparisons on

this binary search, the use of longest common pre-

ﬁx (LCP) of the sufﬁxes, lowers the search time to

O (n+ log(m)) (Gusﬁeld, 1997). The computation of

LCP takes O (m) time.

4.2 Encoding using Sufﬁx Arrays

In order to perform LZ77 encoding with SA, we pro-

ceed as stated in Algorithm 2.

Algorithm 2: SA-Based LZ77 Encoding.

Inputs: D, dictionary with length |D| = m.

S, string to encode, with length |S| = n.

Output: LZ77 description of S on D.

1. Build, in O (mlog(m)) time, the SA for string D

and name it P;

2. To obtain the description (position,length) for

substring S[i. . . n], 0 ≤ i ≤ n, proceed as follows.

a) Do a binary search on vector P until we ﬁnd:

i) the ﬁrst position left, in which the ﬁrst char-

acter of the corresponding sufﬁx matches S[i],

that is, D[P[le ft]] = S[i];

ii) the last position right, in which the ﬁrst char-

acter of the corresponding sufﬁx matches S[i],

that is, D[P[right]] = S[i];

If no sufﬁx starts with S[i] output (0, 0, S[i]), set

i ← i+ 1 and goto 2.

b) From the set of sufﬁxes between P[left] and

P[right], choose the k

sufﬁx, left ≤ k ≤ right,

with a given criteria (see below) obtaining a

given match; let p be the length of that match.

c) Do position ← k and length ← p.

d) Output token (position, length, S[ j]), with j =

i+ length.

e) Do i ← j+ 1; if i = n stop; else goto 2.

In step 2b), it is possible to choose among several

sufﬁxes, according to a given criterion. If we seek

a fast search, we can choose one of the immediate

sufﬁxes, given by left or right. If we want better com-

pression ratio, at the expense of a not so fast search,

we should choose the sufﬁx with the longest match

with substring S[i. . . n]. LZSS encoding can be done

in a similar way, by changing step 2d) according to

the format of the token (1).

Figure 4 ilustrates LZ77 encoding with SA using

dictionary D = mississippi. We present two encoding

situations; the ﬁrst a) considers S = issia, which is

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

Figure 4: LZ77/SS encoding with SA, with dictionary D =

mississippi, showing left and right indexes. In part a) we

encode S = issia, while in part b) we encode S = psi.

encoded by (5, 4, a) or (2, 4, a), depending on how we

perform the binary search and the choice of the match

(steps 3a) and 3b)); in the second example named b),

the string S = psi is encoded by (10, 1, s) or (9, 1, s)

followed by (0, 0, i). It is important to notice that SA

do not have the limitation of ST, presented in subsec-

tion 3.1: no sufﬁx of smaller length preﬁxes another

sufﬁx of greater length.

5 IMPLEMENTATION DETAILS

5.1 Sufﬁx Trees

We have considered the ST construction algo-

rithm available at

marknelson.us/1996/08/01/

suffix-trees/

; when compared to others, this is

the code with the smallest memory requirement for

the ST data structures. This implementation (written

in C++) builds a tree from a string using Ukkonen’s

algorithm (Gusﬁeld, 1997; Ukkonen, 1995) and has

the following main features: it holds a single version

of the string; the tree is composed of branches and

nodes; uses a hash table to store the branches and an

array for the nodes; the Hash is computed as a func-

tion of the number of the node and the ﬁrst character

of the string on that branch, as depicted in Figure 5.

Two main changes in this source code were made: the

Node

was equipped with the number of its parent and

with the counter c

; using the number of its parent,

the code for the propagation of the c

values from a

node was written. After these changes, we wrote the

algorithm presented in subsection 3.2.

5.2 Sufﬁx Arrays

We have used the SA package available at

www.cs.

dartmouth.edu/

doug/sarray/

. It includes the

following functions (among others):

int sarray(int *a, int m);

int *lcp(const int *a, const char *s, int m);

Figure 5: Ilustration of ST data structures. The branch be-

tween nodes 2 and 3, with string “xay” that starts and ends

at positions 4 and 6, respectivelly. The node only contains

its sufﬁx link.

The SA computation by

sarray

is done in time

O (mlog(m)), while the LCP computation by

lcp

takes O (m) time. Using these functions, we imple-

mented the algorithm described in Subsection 4.2.

5.3 Other Details

For both encoders (with ST and SA), we copy the con-

tents of the LAB to the end of the dictionary, only

when the entire contents of the LAB is encoded. An-

other important issue is the fact that for ST (but not

for the SA), we add a terminator symbol to end of the

dictionary, to assure that we have a valid ST. This jus-

tiﬁes the small differences in the compression ratios

attained by the ST and SA encoders.

6 EXPERIMENTAL RESULTS

This section presents the experimental results, using

the LZ77 and LZSS encoders, for dictionaries and

LAB of different sizes. The evaluation was carried

out using standard test ﬁles from the well-known Cal-

gary Corpus

and Canterbury Corpus

. The 18 se-

lected ﬁles are listed in Table 1.

The compression tests were carried out on a ma-

chine with 2GB RAM and an Intel processor Core2

Duo CPU T7300 @ 2GHz. We measured the fol-

lowing parameters: encoding time (seconds), mem-

ory used by the encoder data structures (bytes) and

compression ratio given by

CR = 100



1−

Encoded Size

Original Size



[%], (2)

for the LZSS encoder. The memory indicator refers to

the average ammount of memory needed for every ST

links.uwaterloo.ca/calgary.corpus.html

corpus.canterbury.ac.nz/

SUFFIX ARRAYS - A Competitive Choice for Fast Lempel-Ziv Compressions

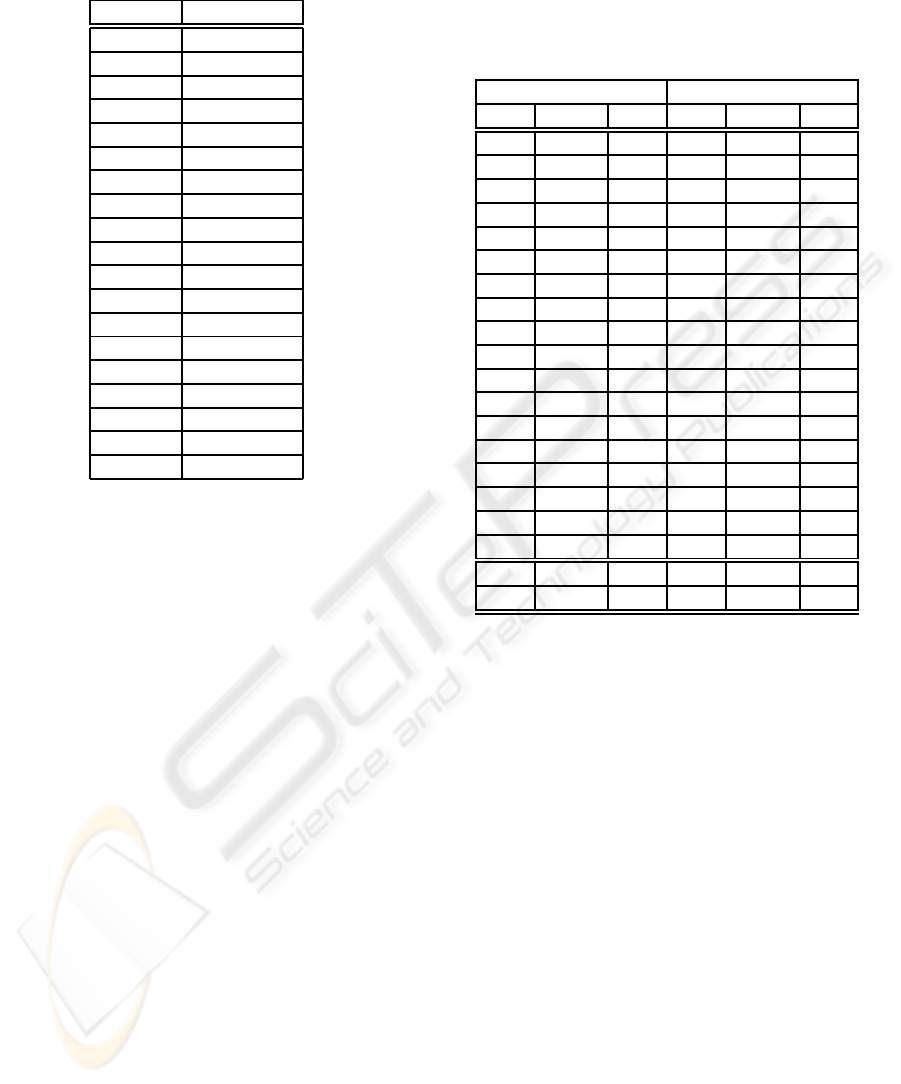
Table 1: Description of the test ﬁles selected from Calgary

Corpus and Canterbury Corpus.

File Size (bytes)

bib 111261

book1 768771

book2 610856

news 377109

paper1 53161

paper2 82199

paper3 46526

paper4 13286

paper5 11954

paper6 38105

progc 39611

progl 71646

progp 49379

trans 93695

alice29 152089

asyoulik 125179

cp 24603

ﬁelds 11150

Total 2680580

and SA, built in the encoding process. The ammount

of memory of each encoder, in detail is

= |Edges| + |Nodes|+ |dictionary|+ |LAB|,

= |Sufﬁx Array| + |dictionary| + |LAB|, (3)

for the ST encoder and SA encoder, repectivelly. We

consider that |.| gives us the memory size (in bytes).

Each ST edge is made up of 4 integers and each node

has 3 integers (each integer has four bytes). On the

SA encoder tests, we have considered the choice of

k as the mid-point between left and right as stated

in Algorithm 2 in Section 4.2. The following subsec-

tions show test results for these ﬁles.

6.1 Dictionary of 128 and LAB of 16

We start by considering a small dictionary with length

128. In this situation, we have a low encoding time

(fast compression) with a reasonable compression ra-

tio. Table 2 presents the results with the 18 ﬁles of

Table 1. By comparing the total time and average

time, we see that SA are slightly faster than ST, but

achieves a lower compression ratio. The ammount of

memory for the SA encoder is ﬁxed at 660 (=129*4

+ 128 +16), while the ST encoder uses much more

memory. For this one, the ammount of memory is

larger and variable, because the number of instantied

edges and nodes depends on the sufﬁxes of the string

in the dictionary.

Table 2: Compression results for (Dictio-

nary,LAB)=(128,16), T is the encoding time in seconds,

M is the average ammount of memory in bytes as in (3),

and CR is the LZSS compression ratio (2) for the ﬁles

described in Table 1. The last two lines correspond to the

average and total values, respectivelly.

ST SA

T M CR T M CR

2.8 4888 37.3 2.9 660 21.6

23.3 4888 40.8 20.4 660 28.0

18.7 5980 42.9 16.2 660 31.2

10.6 6372 38.2 10.0 660 25.2

1.6 4748 42.2 1.4 660 30.4

2.6 5000 42.4 2.2 660 30.5

1.4 4916 41.2 1.2 660 28.8

0.4 4944 42.0 0.4 660 30.0

0.3 5252 42.5 0.3 660 31.0

1.1 5336 43.6 1.1 660 32.7

1.1 5924 45.3 1.1 660 36.3

2.2 5336 48.9 2.0 660 45.1

1.4 5364 49.9 1.3 660 45.2

2.7 7212 44.3 2.5 660 33.2

4.5 5392 42.4 4.1 660 31.8

3.7 5028 41.9 3.3 660 30.3

0.7 5308 42.0 0.7 660 26.7

0.3 6036 51.2 0.3 660 46.2

4.4 5440 43.3 4.0 660 32.5

79.4 97924 71.3 11880

6.2 Dictionary of 128 and LAB of 32

Using a larger LAB, we repeat the experiment and

present the results in Table 3. Comparing the average

and total results of these tables, we conclude that the

increase of the LAB gives rise to a lower compression

time, for both ST and SA, while the compression ratio

is roughly the same. On the tests of Table 3, the SA

encoder is faster than the ST encoder, but this last one

attains a better compression ratio.

6.3 Several Sizes of Dictionary and LAB

Table 4 presents the average values for the 18 ﬁles

of Table 1, using different combinations of dictionary

and LAB lengths. As the length of the dictionary

increases, the ST encoder takes more time and uses

much more memory than the SA encoder. The encod-

ing time of the SA has an interesting behavior.

Figure 6 shows how the encoding time varies with

the length of the dictionary and the LAB, for the test

results of Table 4. We can see that for the ST en-

coder, we get a higher increase and that for the SA

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

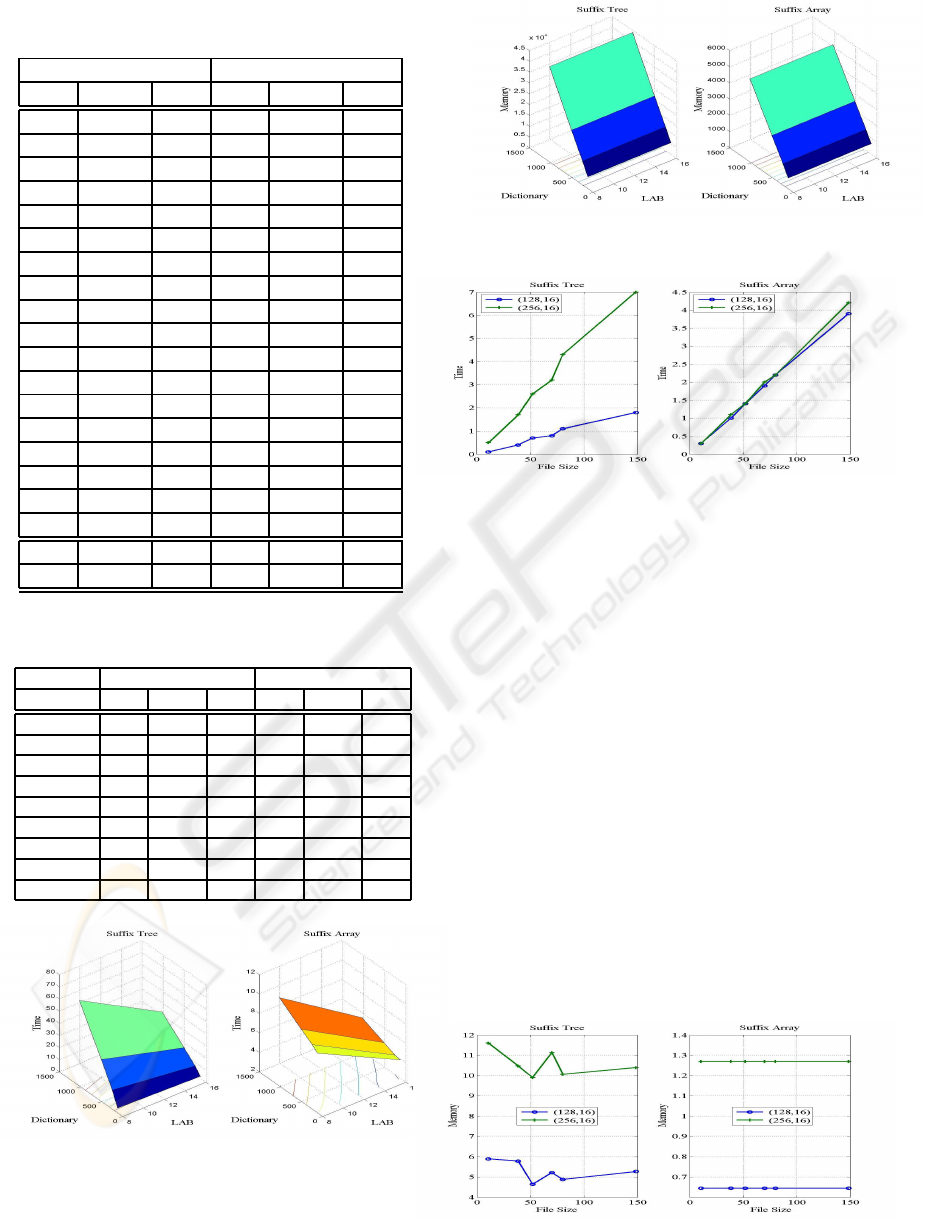
Table 3: Compression results for (Dictio-

nary,LAB)=(256,16).

ST SA

T M CR T M CR

1.3 4904 35.1 1.5 676 22.1

11.5 4932 38.2 10.0 676 27.4

9.0 5996 40.7 7.9 676 30.8

5.1 6388 36.1 4.9 676 24.4

0.8 4876 39.8 0.7 676 29.7

1.2 5044 40.2 1.1 676 30.2

0.7 5072 39.0 0.6 676 28.5

0.2 5044 40.1 0.2 676 30.0

0.2 5408 40.1 0.2 676 30.5

0.6 5352 41.2 0.5 676 32.0

0.5 6220 44.0 0.5 676 36.6

1.1 5296 49.1 1.0 676 45.4

0.7 5380 50.1 0.7 676 45.0

1.3 7228 42.8 1.3 676 33.2

2.3 5408 40.6 2.0 676 31.4

1.8 5044 39.7 1.6 676 30.0

0.3 5184 41.2 0.3 676 28.8

0.2 6080 50.5 0.2 676 47.0

2.2 5492 41.6 1.9 676 32.4

38.8 98856 35.0 12168

Table 4: Compression results for different lengths of dictio-

nary and LAB, over the set of 18 ﬁles listed in Table 1.

ST SA

(Dic,LAB) T M CR T M CR

(128,8) 3.6 5424 42.4 8.1 652 30.3

(128,16) 1.7 5440 43.3 3.9 660 32.5

(256,8) 15.3 11015 43.7 8.6 1292 39.0

(256,16) 7.1 11011 46.0 4.0 1300 41.6

(512,8) 34.4 21776 43.1 9.4 2572 43.6

(512,16) 15.8 21785 46.6 4.5 2580 46.7

(1024,8) 70.3 44136 41.9 11.1 5132 46.0

(1024,16) 32.8 44134 46.6 5.5 5140 49.6

(2048,32) 32.7 88856 46.5 4.5 10276 50.8

Figure 6: Encoding time (in seconds) as a function of the

length of the dictionary and the LAB, for ST and SA en-

coder.

Figure 7: Memory (in kB) as a function of the length of the

dictionary and the LAB, for ST and SA encoder.

Figure 8: Encoding time (in seconds) as a function of the

ﬁle size, for ST and SA encoder.

encoder the increase of the LAB from 8 to 16 low-

ers the encoding time. Figure 7 displays the ammount

of memory as a function of the length of the dictio-

nary and the LAB. The ammount of memory does not

change signiﬁcantly with the length of the LAB. It in-

creases with the length of the dictionary; this increase

is higher for the ST encoder.

6.4 Dictionary of 128/256, LAB of 16

Selecting only a few ﬁles of different contents and

sizes, we narrow our analysis to following 6 ﬁles

(sorted by length): ﬁelds (11150 bytes), progc (39611

bytes), paper1 (53161 bytes), progl (71646 bytes), pa-

per2 (82199 bytes) and alice29 (152089 bytes). Fig-

ure 8 shows the encoding time for these ﬁles, with

dictionary of length 128 and 256 and a LAB of 16,

using ST and SA. For both encoders, we get a linear

Figure 9: Memory (in kB) as a function of the ﬁle size, for

ST and SA encoder.

SUFFIX ARRAYS - A Competitive Choice for Fast Lempel-Ziv Compressions

increase on the encoding time as the ﬁle size grows.

For the ST encoder, we get a larger increase.

Using the same ﬁles, we analyzed the amount of

memory required by both encoders. The results are

depicted in Figure 9, and their analysis leads us to

conclude that the SA encoder needs a much lower am-

mount of memory, that is the same for all ﬁles. The

ST encoder uses a variable ammount of memory and

the increase on the ﬁle size does not always imply an

increase on the necessary ammount of memory.

7 CONCLUSIONS

In this work, we have explored the use of sufﬁx trees

(ST) and sufﬁx arrays (SA) for the Lempel-Ziv 77

family of data compression algorithms, namely LZ77

and LZSS. The use of ST and SA was evaluated in

different scenarios, using standard test ﬁles of differ-

ent types and sizes. Naturally, we focused on the en-

coder side, in order to see how we could perform an

efﬁcient search without spending too much memory.

A comparison between the ST and the SA encoders

was carried out, using the following metrics: encod-

ing time, memory requirement, and compression ra-

tio. Our main conclusions are:

• ST-based encoders require more memory than the

SA counterparts;

• the memory requirement of ST- and SA-based en-

coders is linear with the dictionary size; for the

SA-based encoders, it does not depende on the

contents of the ﬁle to be encoded;

• for small dictionaries, there is no signiﬁcant dif-

ference in terms of encoding time and compres-

sion ratio, between ST and SA;

• for larger dictionaries, ST-based encoders are

slower that SA-based ones; however, in this case,

the compression ratio with ST is slightly better

than the one with SA.

These results support the claim that the use of SA

is a very competitive choice when compared to ST,

for Lempel-Ziv compression. We know exactly the

memory requirement of the SA, which depends on

the dictionary length. In application scenarios where

the length of the dictionary is large and the available

memory is scarce (e.g., a mobile device), it is prefer-

able to use SA instead of ST.

As future work, we intend to develop the SA en-

coder combining LCP and the simple accelerant and

supper accelerant (Gusﬁeld, 1997, p´ag. 152, 153), to

speed up the search over the dictionary. This issue is

of greater importance for dictionaries of large dimen-

sions.

REFERENCES

Abouelhoda, M., Kurtz, S., and Ohlebusch, E. (2004). Re-

placing sufﬁx trees with enhanced sufﬁx arrays. Jour-

nal of Discrete Algorithms, 2(1):53–86.

Fiala, M. and Holub, J. (2008). DCA using sufﬁx arrays. In

Data Compression Conference DCC2008, page 516.

Gusﬁeld, D. (1997). Algorithms on Strings, Trees and Se-

quences. Cambridge University Press.

Karkainen, J., Sanders, P., and S.Burkhardt (2006). Linear

work sufﬁx array construction. Journal of the ACM,

53(6):918–936.

Larsson, N. (1996). Extended application of sufﬁx trees to

data compression. In Data Compression Conference,

page 190.

Larsson, N. (1999). Structures of String Matching and Data

Compression. PhD thesis, Department of Computer

Science, Lund University, Sweden.

Manber, U. and Myers, G. (1993). Sufﬁx arrays: a new

method for on-line string searches. SIAM Journal on

Computing, 22(5):935–948.

McCreight, E. (1976). A space-economical sufﬁx tree con-

struction algorithm. Journal of the ACM, 23(2):262–

272.

Sadakane, K. (2000). Compressed text databases with efﬁ-

cient query algorithms based on the compressed sufﬁx

array. In ISAAC’00, volume LNCS 1969, pages 410–

421.

Salomon, D. (2007). Data Compression - The complete ref-

erence. Springer-Verlag London Ltd, London, fourth

edition.

Sestak, R., Lnsk, J., and Zemlicka, M. (2008). Sufﬁx array

for large alphabet. In Data Compression Conference

DCC2008, page 543.

Storer, J. and Szymanski, T. (1982). Data compression via

textual substitution. Journal of ACM, 29(4):928–951.

Ukkonen, E. (1995). On-line construction of sufﬁx trees.

Algorithmica, 14(3):249–260.

Weiner, P. (1973). Linear pattern matching algorithm. In

14th Annual IEEE Symposium on Switching and Au-

tomata Theory, volume 27, pages 1–11.

Zhang, S. and Nong, G. (2008). Fast and space efﬁcient

linear sufﬁx array construction. In Data Compression

Conference DCC2008, page 553.

Ziv, J. and Lempel, A. (1977). A universal algorithm for

sequential data compression. IEEE Transactions on

Information Theory, IT-23(3):337–343.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications