BIRTH-DEATH FREQUENCIES VARIANCE OF SINUSOIDAL

MODEL

A New Feature for Audio Classification

Shahrokh Ghaemmaghami

and Jalil Shirazi

Sharif University of Technology, Tehran, Iran

Islamic Azad University, Gonabad Branch, Gonabad, Iran

Keywords: Audio classification, sinusoidal model.

Abstract: In this paper, a new feature set for audio classification is presented and evaluated based on sinusoidal

modeling of audio signals. Variance of the birth-death frequencies in sinusoidal model of signal, as a

measure of harmony, is used and compared to typical features as the input into an audio classifier. The

performance of this sinusoidal model feature is evaluated through classification of audio to speech and

music using both the GMM and the SVM classifiers. Classification results show that the proposed feature is

quite successful in speech/music classification. Experimental comparisons with popular features for audio

classification, such as HZCRR and LSTER, are presented and discussed. By using a set of three features, we

achieved 96.83% accuracy, in one-sec segment based audio classification.

1 INTRODUCTION

Rapid increase in the amount of audio data demands

for an automated method that allows for efficient

segmentation and classification of audio stream

based on its contents. In multimedia applications,

such systems can be useful to achieve automatic

classification, indexing, archiving, and retrieving of

information from large multimedia corpora. Audio

segmentation and classification also have significant

applications in data retrieval, archive management,

modern human-computer interfaces, and

entertainment.

One of basic problems in audio segmentation and

classification is speech/music discrimination. By

rejecting non-speech segments, speech/music

discrimination can play a signification role in speaker

and speech recognition systems. The new generation

of low rate coders and compression technologies

need an estimation of the signal nature to achieve a

higher compression rate. Among them is the work by

EI-Maleh et al. (

Ei-Maleh, 2000) that used LSF (Line

Spectral Frequency) parameters and zero crossing for

frame based speech/music discrimination.

Ajmera et al. (Ajmera, 2002) employed a

posteriori probability based entropy and dynamism

features and reported 82.5% and 79.2% accuracies

for speech and music segments, respectively.

Saunders (Saunders, 1996) used typical features,

such as zero crossing rate and short-time energy, for

a radio broadcast speech/music classifier. For a 2.4

sec segment of audio signals, this work achieved an

accuracy of 98%. Scheirer and Slaney introduced an

audio classification method in (Scheirer, 1997) using

more features and performed experiments based on

different classification models. For the same segment

length of an audio signal (2.4 sec), the overall error

reported was of as low as 1.4%.

Lu et al. (Lu, 2002) applied an algorithm based

on KNN (K-Nearest Neighbor) classifier and LSP

(Line Spectral Pair) -VQ (Vector Quantization) to

determine speech/non-speech segments. Some other

classification approaches have recently been

introduced in the literature that use different

methods, such as nearest feature line (Li, 2000) and

SVM (Support Vector Machine) (Guo, 2003).

In this paper, we propose a sinusoidal model

based feature for audio classification to speech and

music by using the GMM (Gaussian Mixture Model)

and the SVM classifiers. The sinusoidal models of

different orders are tested and evaluated. The model

feature, variance of birth-death frequencies, is

presented and compared to conventional features, e.g.

HZCRR (high zero crossing rate ratio) and LSTER

139

Ghaemmaghami S. and Shirazi J. (2008).

BIRTH-DEATH FREQUENCIES VARIANCE OF SINUSOIDAL MODEL - A New Feature for Audio Classiﬁcation.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 139-144

DOI: 10.5220/0001937601390144

 SciTePress

(low short time energy ratio), in terms of the

classification performance.

Figure 1: Birth and death of sinusoidal tracks.

This paper is structured as follows. Sinusoidal

modeling of speech signals is briefly described in

section 2. The features used in this study and the

classification methods we have employed are

presented in section 3. The system implementation

and experimental results are presented in section 4

and the features and the classification techniques are

compared in section 5. The paper is concluded in

section 6.

2 SINUSOIDAL MODEL

In this section, a brief overview of sinusoidal

modeling is given and the frequency tracking in the

sinusoidal model is presented.

2.1 McAulay-Quatieri Sinusoidal Model

The McAulay-Quatieri (MQ) algorithm is often used

to produce a sinusoidal representation of sounds

(McAulay, 1986). The algorithm assumes that a large

class of acoustical waveforms can be represented by

a collection of sinusoidal components described by

amplitudes, phases, and frequencies. These

parameters are estimated from the short-time Fourier

transform using a simple peak-picking algorithm.

The sampled sound is first transformed into a two-

dimensional time-frequency representation. Next, the

regions of high time-frequency energy are located,

where the slope of the waveform changes from

positive to negative. The voiced regions can be

modeled by a set of harmonically related sinusoids,

while the unvoiced regions are modeled using non-

harmonic sinusoids.

As the fundamental frequency changes, the

number of peaks from frame to frame changes. The

concept of sinusoidal births and death is used to

explain the movement of spectral peaks between

frames. In order to match spectral peaks, tracks are

formed by connecting peaks between adjacent

frames. A track is dead when there is no peak in the

current frame within

of the frequency of a peak

in the next frame. Correspondingly, a new track is

born if the frequency of a peak in the current frame is

not within

of the frequency of a peak in previous

frame.

Fig. 1 shows the birth and death of frequency

tracks formed by connecting peaks of similar

frequencies between frames.

3 PROPOSED FEATURES AND

ALGORITHMS

In this section, the features extracted in this study are

presented. Then, a brief overview of the GMM and

the SVM classifiers, which we have employed to

evaluate the performance of the proposed features, is

given.

3.1 Feature Analysis

In order to achieve a high accuracy in audio

classification and segmentation, it is critical to

extract features that can capture the major temporal-

spectral characteristics of the signals. To classify

one-second audio segments, we selected: the

HZCRR, the LSTER and a new feature as a measure

of the harmony called BDFV (birth-death

frequencies variance). These features will be

described in detail in this section.

3.1.1 The HZCRR

This feature describes the variations of zero crossing

rates (ZCR). The HZCRR is defined as the ratio of

the number of frames whose zero crossing rates are

grater than 1.5 time of average zero crossing rate in a

one-second window, as:

[]

∑

−

+−=

1)5.1)(sgn(

avZCRnZCR

HZCRR

(1)

where n is the frame index, ZCR(n) is the zero

crossing rate at frame n, avZCR is the average ZCR,

sgn is sign function, and N is the total number of

frames in a one-second window (Lu, 2002).

Normally, speech signals are composed of alternating

high energy voiced sounds and low energy unvoiced

sounds; while music signals usually do not follow

this structure. Therefore, for music signals, the

HZCRR is usually lower than that of speech.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

140

3.1.2 The LSTER

This feature describes the variations of short time

energy (STE). The LSTER is defined as the ratio of

the number of frames having energy greater than a

half of the average short time energy in a one-second

window, as:

[]

∑

−

+−=

1))(5.0sgn(

nSTEavSTE

LSTER

(2)

where n is the frame index, STE(n) is the short time

energy at frame n, avSTE is the average STE, and N

is the total number of frames in a one-second window

(Lu, 2002).

Normally, there are more silence frames in

speech than those in music. Therefore, music signals

have a lower LSTER, as compared to speech, in

general.

3.1.3 The Birth-death Frequencies Variance

This feature describes a measure of the harmony. A

detailed spectral analysis shows that pure music is

more harmonious than speech, since pure speech

contains a sequence of tonal (vowels) and noise-like

(consonants) sounds. Speech is characterized by a

formantic structure, whereas music is characterized

by harmonic structure. The music spectra change

more slowly than speech spectra. Music can be

regarded as a succession of periods of relatively

stable notes and phones, where speech is rather a

rapid succession of noisy periods, such as unvoiced

consonants, and of periods of relatively stable parts,

e.g. vowels.

Speech signals may hardly have a long time

periodic structure. Hence, for speech signal, the

harmony measure in general could be lower than that

of music. This diversity forms our main motivation

for applying sinusoidal modeling, as the technique

for measuring the harmony to the audio classification

problem. Expectedly, a feature of birth and death of

frequencies can discriminate between music and

speech signal quite well, due to diversity in the

harmonic structure.

In this work, the audio signal is divided into

overlapping frames, and then sinusoidal model

analysis is applied to the audio signal in each frame.

Thus, for each frame, a set of frequencies is

generated. These frequency vectors are used for

tracking frequencies. We tested two measures of

tracking frequencies in a one-second window as the

feature. These two measures are: 1) sum of the birth-

death frequencies and 2) variance of the birth-death

frequencies (BDFV) in the one-second window.

We found the latter feature, BDFV,

outperforming the sum of the birth-death frequencies

in all cases in our classification tests. Henceforth, we

just focus on the BDFV in this paper, for the task of

audio classification, which is defined as:

∑

−

−=

))((

avBDnBD

BDFV

(3)

where n is the frame index, BD(n) is the short time

birth-death frequencies number at frame n, avBD is

the average BD, and N is the total number of frames

in a one-second window.

3.2 Classification Algorithms

3.2.1 Support Vector Machines

In this method, the data is mapped into a high

dimensional space via a nonlinear map, and an

optimal separating hyper-plane, or linear regression

function, is constructed in this space. Given a class

labeled training feature vectors, class boundaries

between two classes are learned through the SVM.

The SVM minimizes the structural risk and can

realize nonlinear discrimination by kernel mapping.

Let

{, }

iii

be a set of N training data points,

where

x ∈R denotes the i-th input data and

{1, 1}

∈

−+

is the class label of the data. The SVM

aims at finding a classifier of the form:

() ( ,)

ii i

yx sign yKx x b

⎡

⎤

⎢

⎥

⎣

⎦

∑

(4)

where

are positive real constants,

is a real

constant,

(,) (),()

Kx x x x

φφ

,••

is the inner

product, and

()

is the nonlinear map from original

space to the high dimensional space.

The SVM decision function is obtained under

constraints:

∑

,....,1 0 NiC

=≤≤

where C is a parameter that allows for specifying

how strictly we want the classifier to fit into the

training data

(Guo, 2003).

3.2.2 Gaussian Mixture Model

The GMM classifier models each class of data as the

union of a few multidimensional Gaussian clusters in

the feature space. A GMM is fully represented by:

the mean vectors, covariance matrices, and the

BIRTH-DEATH FREQUENCIES VARIANCE OF SINUSOIDAL MODEL - A New Feature for Audio Classification

141

mixture weights. Given a sequence of feature vectors,

a GMM is trained using the well-known expectation-

maximization (EM) algorithm. The probability

density function of the mixture model of dimension

d, for class i, is given as:

∑

),,()(

kki

ΓμXW

∑

(5)

where W

denotes the class of the signal, X indicates

the feature vector,

μ is for the d-component mean

vector,

Γ is the d×d covariance matrix, and

denotes the mixing probabilities. The GMM

classification uses a likelihood estimate for each

model, which measures how well the new data point

is modeled by the entrained Gaussian clusters. An

unknown vector X in the feature space is assigned to

the class that is found to be the best model for this

vector.

4 EXPERIMENTS

The "music-speech" corpus used in this study is a

collection of 240 15-sec sound files, randomly

selected from the radio programs (Scheirer, 1997).

This corpus is taken as a standard benchmark for

audio system evaluations and has been used in many

audio classification studies (see (Scheirer, 1997) and

(

Berenzweig, 2001)).

For the feature extraction, the audio signal is

partitioned into Hamming windowed frames of 23.2

ms long, with 11.2 ms overlap. The classifier is

evaluated using labeled data sets, each 20 minutes of

speech and music data. Each model is trained with 60

15-sec long training speech files (900 seconds) and

60 15-sec training vocal and non-vocal music files

(900 seconds). Each system tested over 20 15-sec

speech files (300 seconds), 20 15-sec vocal music

files (300 seconds), and 21 15-sec non-vocal music

files (315 seconds). Thus, each system is trained over

120 15-sec files, (1800 seconds) and is tested with 61

15-sec files (915 seconds). For each frame, the

sinusoidal models of different orders are used and

zero padding is employed to increase the peak

detection accuracy (

Smith, 1987). Thus, for each

frame, a set of frequencies in addition to two values

of ZCR and STE are generated.

Fig. 2 shows the probability distribution curves of

the HZCRR for music and speech signals. The curves

obtained from the database training files using one-

second window. As shown, there are overlaps

between these two curves and the cross point of two

curves, as a threshold, is 0.11. Fig. 3 shows the

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

HZCRR PDF

HZCRR Value

Probablity

Music

Speech

Figure 2: Probability distribution curves of HZCRR.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

LSTER PDF

LSTER Value

Probablity

Music

Speech

Music

Speech

Figure 3: Probability distribution curves of LSTER.

probability distribution curves of LSTER for music

and speech signals obtained from the database, where

the cross point of two curves, as a threshold, is 0.32.

Figures 4 and 5 show the BDFV curves for music

and speech signals for different orders of the

sinusoidal model. The curves are obtained from the

training database using one-second window (86

frames), where the horizontal axis shows the number

of frames. Fig. 6 shows the probability distribution

curves of the BDFV for music and speech signals for

sinusoidal model of order 15. The cross point of two

curves, as a threshold, is 15.5. For music, almost no

BDFV value is above 24.

It is observed in these figures that the BDFV

values for speech are in general higher than those for

music. This is because music is more harmonious and

stable than speech. Therefore, the BDFV is an

effective feature for discriminating speech and music.

The resulting error indicated that no additional

improvement to the signal discrimination was

achieved, when we increased the sinusoidal model

order from 15. Hence, we used sinusoidal model of

order 15 in our experiments.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

142

In our experiments, we conducted a comparative

evaluation over these three described features. At

first, only one feature was used to discriminate

speech from music, where the cross point of two pdfs

was used as the threshold. The classification errors

are presented in table 1. As shown, the BDFV is an

effective feature for discriminating between speech

and music signals and yields a higher performance,

as compared to the other features.

0 10 20 30 40 50 60 70 80 90

Birth-death frequencies variance-15

Birth-death frequencies vari ance-15 Value

Seconds/10

Music

Speech

Figure 4: BDFV curves, with sinusoidal model of order 15.

0 10 20 30 40 50 60 70 80 90

100

110

Birth-death frequencies variance-25

Birt h-death frequencies variance-25 Val ue

Seconds/10

Speech

Music

Figure 5: BDFV curves, with sinusoidal model of order 25.

5 10 15 20 25 30 35 40 45 50

0.5

1.5

2.5

3.5

4.5

x 10

-3

Birth-death frequencies variance-15 PDF

Birth-death frequencies variance-15 Value

Probablity

Music

Speech

Figure 6: Probability distribution curves of BDFV, with

sinusoidal model of order 15.

Table 1: Classification errors (percentage) with HZCRR,

LSTER and BDFV using the pdfs’ cross-point as threshold.

Total

Length

(sec)

→

300

315 300 915

Features

↓

Speech

Non-

Vocal

Music

Vocal

Music

Total

HZCRR 5 27.61 12.78 23.93

LSTER 16.66 13.96 2.18 12.45

BDFV

18.33 8.57 0.32

9.28

The classification method mentioned so far could

result in high classification accuracy with optimal

thresholds. However, this optimality is almost

unreachable due to actual dependence of thresholds

on the signal characteristics. Therefore, we employed

the GMM and the SVM classifiers which are not

based on a thresholding procedure. We used different

combinations of two conventional features, the

HZCRR and the LSTER, with the BDFV, as the

feature vector of one-second signal and used both the

GMM and the SVM based classification methods for

evaluating the performance of the BDFV.

In the experiments, we used the radial basis

function (RBF) kernel and the parameters C=10 and

σ =1 for the SVM classifier. The second

classification approach was to use the GMM

classifier to model each class of data, speech or

music. At the training step, the feature vectors from

each class are used to train the GMMs. The GMM

parameters are estimated by the EM algorithm and

the classification of an unknown vector was done by

finding the class whose Gaussian distribution came

with the highest probability to produce the vector.

5 RESULTS AND DISCUSSION

We examined the GMM with different numbers of

Gaussians, and found that the optimal order was 4 for

the speech models and 4 for the music models, when

the three described features were used. We made the

same examination with different combinations of the

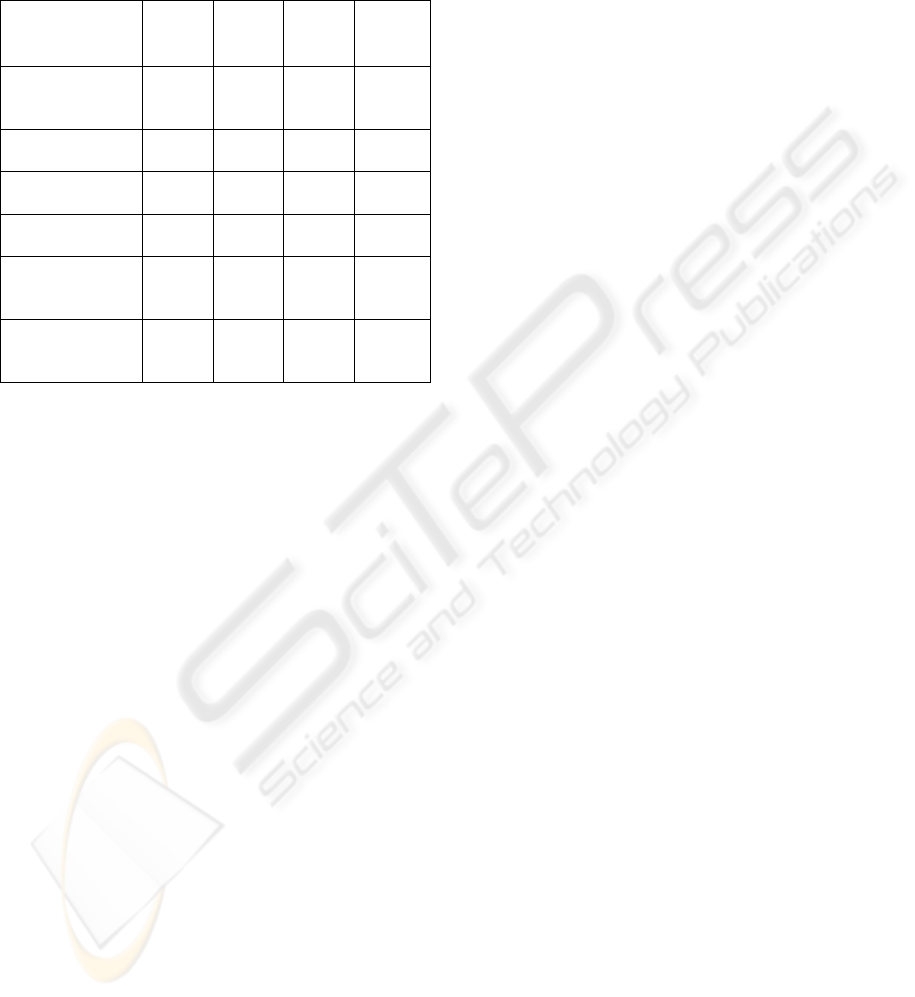
features using the SVM classifier. Table 2 shows the

resulting performance using the three features and the

two classifiers. As indicated, the SVM and the GMM

classifiers significantly improve the accuracy when

all the three features are used. It is indicated that the

total error introduced using the HZCRR and the

LSTER is 12.13%, as compared to the error of 5.46%

introduced using the HZCRR and the BDFV, and

4.91% using the LSTER and the BDFV. These

BIRTH-DEATH FREQUENCIES VARIANCE OF SINUSOIDAL MODEL - A New Feature for Audio Classification

143

results show a significant improvement to the

classification accuracy obtained from combining the

new feature with the HZCRR, the LSTER, or both.

Table 2: Classification errors (percentage) with different

combinations of the three features using SVM and GMM.

As observed, the total errors introduced using the

three features are 4.69% and 3.17% with the SVM

and the GMM classifiers, respectively. To ensure the

effectiveness of the proposed features, evaluation of

the classification performance is extended to file-

level, in addition to the segment-level evaluation

(one-second window) described earlier. We made this

evaluation based on a majority voting strategy at file-

level. We used the same speech-music database in

this test and reached just 1.63% error, i.e. one speech

file out of 61 speech-music test files.

As shown in table 2, better classification results

are achieved over music files, as compared to speech,

when the

BDFV is used. Most sounds generated by

musical instruments have a harmonic structure,

which is not the case with speech signals that may

have a mixed harmonic/non-harmonic structure due

to their diverse voicing characteristics. This diversity

is well identified by the sinusoidal model that

measures the harmony of the audio signals.

Nevertheless, the BDFV feature of the sinusoidal

model plus the HZCRR and the LSTER form a

powerful feature set for speech/music discrimination.

Still, further performance improvement could be

expected to achieve by combining other features of

the sinusoidal model as an extension to this work.

6 CONCLUSIONS

In this study, we have proposed a new feature based

on the sinusoidal model, called BDFV, for audio

classification to speech and music. This feature is the

variance of the birth-death frequencies in the

sinusoidal model of an audio signal, as a measure of

the harmony. Our classification results show a high

discriminating performance of this feature, as

compared to typical features such as the HZCRR and

the LSTER features that are widely used for audio

classification. It is also revealed that a higher

classification performance is achieved, by combining

this new feature with the HZCRR and the LSTER,

which has been evaluated using the model-based,

insensitive to threshold GMM and the SVM

classifiers. Through this work, it has been shown that

the sinusoidal model features are very effective in

audio classification, due to capability of the model to

identify the harmonic structure.

REFERENCES

Ei-Maleh, K., Klein, M., Petrucci, G., kabal, P. 2000.

Speech/music discrimination for multimedia

Applications. In Proc ICASSP- 2000, pp. 2445-2448.

Ajmera, J., McCowan, I., Bourlard, H., 2002. Robust

HMM based speech/music segmentation. In Proc

ICASSP- 2002, pp. 297-300.

Saunders, J., 1996. Real-time discrimination of broadcast

speech/music. In Proc ICASSP-96, pp. 993-996.

Scheirer, E., Slaney, M., 1997. Construction and evaluation

of a robust multifeature speech/music discriminator. In

Proc. ICASSP- 97, pp. 21-24.

Lu, L., Zhang, H.-J., 2002. Content Analysis for Audio

Classification and Segmentation. In IEEE Trans.

Speech & Audio Proc., vol. 10, pp. 504 – 516.

Li, S. Z., 2000. Content-based audio classification and

retrieval using the nearest feature line method.In IEEE

Trans. Speech & Audio Proc., vol. 8, pp. 619 – 625.

McAulay, R., Quatieri, T., 1986. Speech analysis/synthesis

based on a Sinusoidal representation. In IEEE Trans.

Acous., Speech & Sig. Proc., Vol. ASSP-34, No.4, pp.

744-754.

Smith, J. O., Serra, X., 1987. PARSHL: An

analysis/synthesis program for non-harmonic sound

based on Sinusoidal representation. In http://www-

ccrma.stanford.edu/~jos/parshl/parshl.pdf.

Berenzweig, A. L., Ellis, D. P. W., 2001. Locating singing

voice segments within music signals. In Proc IEEE

WASPAA, Mohonk NY, pp. 119–122.

Guo, G., Li, S. Z., 2003. Content-based audio

classification and retrieval by support vector machines.

In IEEE Trans. Neural Networks Proc., vol. 14, pp.

209-215.

915 300 315 300

Total Length

(sec)

→

Total

Vocal

Music

Non-

Vocal

Music

Speech

Features/

Classifier

↓

12.13 10.66 15.87 9.66 HZCRR+

LSTER/SVM

5.46 0.66 2.53 13.33 HZCRR+

BDFV/SVM

4.91 0.33 2.22 12.33 LSTER+

BDFV/SVM

4.69

0 2.22 12 HZCRR+

LSTER+

BDFV/SVM

3.17

0.66 1.58 9.66 HZCRR+

LSTER+

BDFV/GMM

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

144