
HMM INVERSION WITH FULL AND DIAGONAL COVARIANCE
MATRICES FOR AUDIO-TO-VISUAL CONVERSION
Lucas D. Terissi and Juan C. G´omez
Laboratory for System Dynamics and Signal Processing, FCEIA, Universidad Nacional de Rosario
CIFASIS, CONICET, Riobamba 245bis, Rosario, Argentina
Keywords:
Hidden Markov Models, Audio-Visual Speech Processing, Facial Animation.
Abstract:
A speech driven MPEG-4 compliant facial animation system is proposed in this paper. The main feature
of the system is the audio-to-visual conversion based on the inversion of an Audio-Visual Hidden Markov
Model. The Hidden Markov Model Inversion algorithm is derived for the general case of considering full
covariance matrices for the audio-visual observations. A performance comparison with the more common
case of considering diagonal covariance matrices is carried out. Experimental results show that the use of full
covariance matrices is preferable since it leads to an accurate estimation of the visual parameters, yielding the
same performance as in the case of using diagonal covariance matrices, but with a less complex model.
1 INTRODUCTION
The widespread use of multimedia applications such
as computer games, online virtual characters, video
telephony, and other interactive human-machine in-
terfaces, has made speech driven animation of vir-
tual characters to play an increasingly important role.
Several approaches have been proposed in the litera-
ture for speech driven facial animation. Among the
different models used to generate the visual infor-
mation (animation parameters) from speech data, the
ones based on Hidden Markov Models (HMM) have
proved to yield more realistic results.
In the approach proposed by Yamamoto et al (Ya-
mamoto et al., 1998), an HMM is learned from au-
dio training data and each video training sequence is
aligned with the audio sequence using Viterbi opti-
mization (Viterbi, 1967). In the synthesis stage, the
Viterbi alignment algorithm is used to select an opti-
mal HMM state sequence for a novel audio and the
visual output associated with each state in the au-
dio sequence is retrieved. This technique provides
video predictions of limited quality because the out-
put of each state is the average of the Gaussian mix-
ture components associated to that state, which is
only indirectly related to the current audio vector
by means of the Viterbi state. Rao and Chen (Rao
et al., 1998), (Chen, 2001) proposed a mixture based
joint audiovisual HMM, least mean square estimation
method is employed for the synthesis phase and the
visual output is made dependent not only on the cur-
rent state, but also on the current audio input, resulting
in improved performance. Brand (Brand, 1999) pro-
posed a cross-modal HMM under the assumption that
both acoustic and visual data can be modeled with the
same structure. The training is conducted using video
data. Once a video HMM is learned, the video out-
put probabilities at each state are remapped onto the
audio space using the M-step in Baum-Welch algo-
rithm (Baum and Sell, 1968).
All the above methods rely on the Viterbi algo-
rithm which is rather sensitive to noise in the audio
input. To address this limitation, Choi et al (Choi
et al., 2001) have proposed a Hidden Markov Model
Inversion (HMMI) method for audio-visual conver-
sion. HMMI was originally introduced in (Moon and
Hwang, 1995) in the contextof robust speech recogni-
tion. In HMMI, the visual output is generated directly
from the given audio input and the trained HMM by
means of an expectation-maximization (EM) itera-
tion, thus avoiding the use of the Viterbi sequence
and improving the performance of the estimation (Fu
et al., 2005). Recently, Xie et al (Xie and Liu,
2007) proposed a coupled HMM approach and de-
rived an expectation maximization (EM)-based A/V
conversion algorithm for the CHMMs, which con-
verts acoustic speech into decent facial animation pa-
rameters.
In this paper, a speech driven MPEG-4 compliant
facial animation system is proposed. A joint audio-
168
D. Terissi L. and C. Gómez J. (2008).
HMM INVERSION WITH FULL AND DIAGONAL COVARIANCE MATRICES FOR AUDIO-TO-VISUAL CONVERSION.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 168-173
DOI: 10.5220/0001941001680173
Copyright
c
SciTePress
Audio
Audio
Visual
Features
Features
Audio-Visual
Audio-Visual
Audio-Visual
Conversion
Model
AV-HMM
Training
TRAINING
SYNTHESIS
Training Data
Feature
Feature
Extraction
Extraction
Re-Training Data
FAP
Estimation
Speech
MPEG-4 Facial
Animation
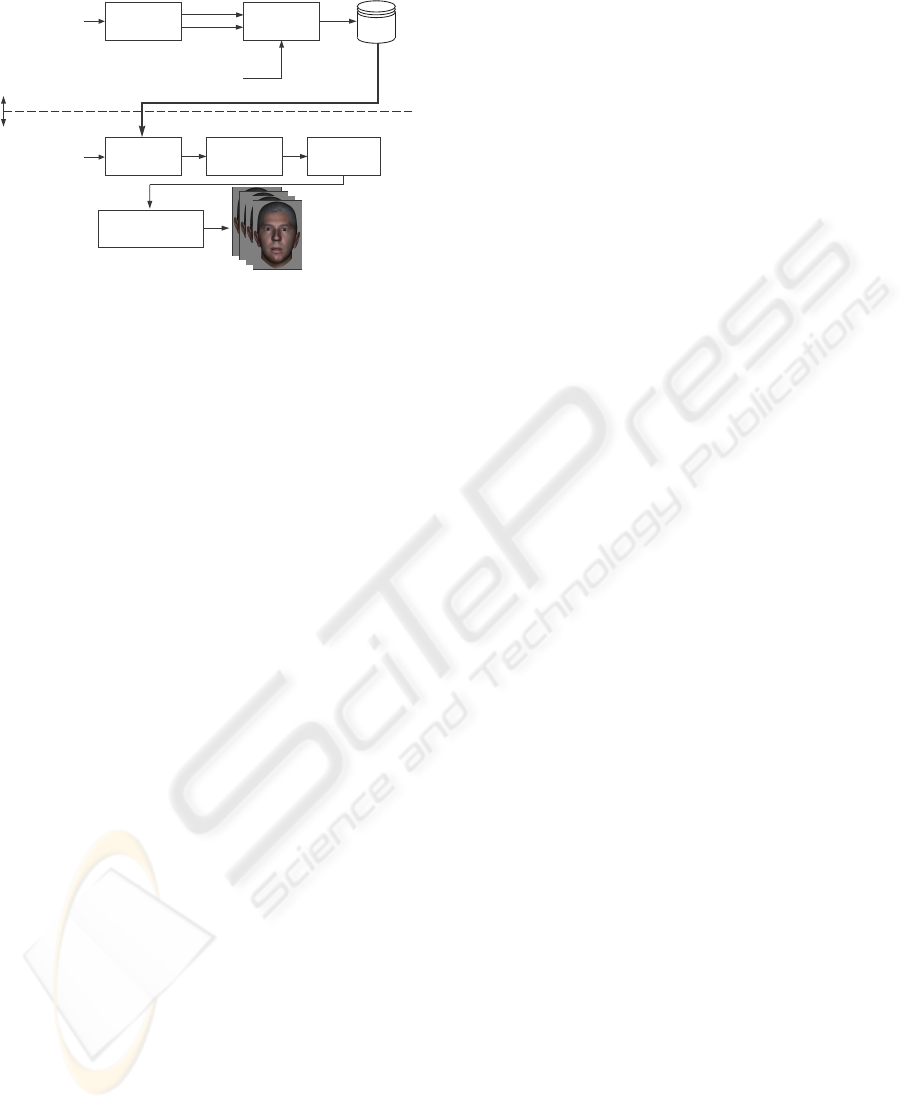
Figure 1: Schematic representation of the speech driven an-
imation system.
visual Hidden Markov Model (AV-HMM) is trained
using audio-visual data and then Hidden Markov
Model inversion is used to estimate the animation pa-
rameters from speech data. The feature vector corre-
sponding to the visual information during the train-
ing is obtained via Independent Component Analysis
(ICA). Previous approaches based on HMMs consider
diagonal covariance matrices for the audio-visual ob-
servation, invoking reasons of computational com-
plexity. In this paper, the use of full covariance ma-
trices is investigated. Simulation results show that
the use of full covariance matrices leads to an accu-
rate estimation of the visual parameters, yielding the
same performance as with diagonal covariance matri-
ces, but with a less complex model and without af-
fecting significantly the computational load.
The rest of the paper is organized as follows. An
overviewof the speech driven facial animation system
is presented in section 2. The AV-HMM is introduced
in section 3, where a Hidden Markov Model Inversion
algorithm for the general case of considering full co-
variance matrices for the audio-visual observations is
also derived. In section 4, the proposed algorithm for
feature extraction is described. The MPEG-4 com-
pliant facial animation technique is presented in sec-
tion 5. Experimental results and some concluding re-
marks are included in sections 6 and 7, respectively.
2 SYSTEM OVERVIEW
A block diagram of the proposed speech driven ani-
mation system is depicted in Fig. 1. An audiovisual
database is used to estimate the parameters of a joint
AV-HMM. This database consists of videos of a talk-
ing person with reference marks in the region around
the mouth, see Fig. 2(a).
In a first training stage, feature parameters of the
audiovisual data are extracted. The audio part of the
feature vector consists of mel-cepstral coefficients,
while the visual part are the coefficients in a ICA rep-
resentation of the above mentioned set of reference
marks. In a second training stage, the audio part of
the AV-HMM is re-trained using audio data from a
speech-only database. Re-training only the audio part
of the model allows to obtain a more robust model
against inter-speaker variability, avoiding the need to
record videos of speakers with the reference marks on
their faces.
For the speech driven animation, speech data is
used to estimate the visual features by inversion of the
AV-HMM using a technique described in section 3.
From these data, Facial Animation Parameters (FAPs)
of the MPEG-4 (ISO/IEC IS 14496-2, Visual, 1999)
standard are computed to generate the facial anima-
tion.
3 AUDIO VISUAL MODEL
In this paper, a joint AV-HMM is used to represent
the correlation between the speech and facial move-
ments. The AV-HMM, denoted as λ
av
, is character-
ized by three probability measures, namely, the state
transition probability distribution matrix (A), the ob-
servation symbol probability distribution (B) and the
initial state distribution (π), and a set of N states
S = (s
1
,s
2
,...,s
N
), and audiovisual observation se-
quence O
av
= {o
av1
,...,o
avT
}. In addition, the obser-
vation symbol probability distribution at state j and
time t, b
j
(o
avt
), is considered a continuous distribu-
tion which is represented by a mixture of M Gaussian
distributions
b
j
(o
avt
) =
M
∑
m=1
c
jm
N (o
at
,o
vt
,µ
jm
,Σ
jm
) (1)
where c
jm
is the mixture coefficient for the m-
th mixture at state j and N (o
at
,o
vt
,µ
jm
,Σ
jm
) is a
Gaussian density with mean µ
jm
and covariance Σ
jm
.
The audiovisual observation o
avt
is partitioned as
o
avt
,
o
T
at
,o
T
vt
T
, where o
at
and o
vt
are the audio
and visual observation vectors, respectively.
A single ergodic HMM is proposed to repre-
sent the audiovisual data. An alternative to an er-
godic model, would be a set of left-to-right HMMs
representing the different phonemes (with associated
visemes) of the particular language. These models
have been used in the context of speech modeling by
several authors, see for instance (Xie and Liu, 2007).
An ergodic model provides a more compact repre-
sentation of the audiovisual data, without the need of
HMM INVERSION WITH FULL AND DIAGONAL COVARIANCE MATRICES FOR AUDIO-TO-VISUAL
CONVERSION
169

phoneme segmentation, which is required when left-
to-right models are used. In addition, this has the ad-
vantage of making the system adaptable to any lan-
guage.
3.1 AV-HMM Training
The training of the AV-HMM consists of two stages,
each one using a different database. In the first train-
ing stage, an audiovisual database consisting of a
set of videos of a single talking person with refer-
ence marks drawn on the region around the mouth,
is used to estimate the parameters of an ergodic AV-
HMM, resorting to the standard Baum-Welch algo-
rithm (Baum and Sell, 1968). Details on the com-
position of the audiovisual feature vector are given
in Section 4, where procedures to take into account
audio-visual synchronization and co-articulation are
also described. In the second training stage, a speech-
only database consisting of audio recordings from a
set of talking persons is employed to re-train the au-
dio part of the AV-HMM, leading to a speaker inde-
pendent model. The re-training is carried out using
an only audio HMM (hereafter denoted as A-HMM),
with the same structure, which is constructed from the
AV-HMM. The A-HMM has the same transition prob-
ability and initial state probability matrices obtained
in the first stage, while the corresponding observation
symbol probability distribution is re-estimated from
the speech-only database. The observation symbol
probability distribution is parameterized by µ
jm
, Σ
jm
and c
jm
, see eq. (1). To emphasize the mix composi-
tion of the AV-HMM, the mean and covariance para-
meters can be partitioned as
µ
jm
=
µ
a
jm
µ
v
jm
Σ
jm
=
Σ
a
jm
Σ
av
jm
Σ
va
jm
Σ
v
jm
(2)
where the superscript a and v denote the audio and
visual parts, respectively. During the second train-
ing stage, only µ
a
jm
and Σ
a
jm
are re-estimated using the
speech-only data. Finally, the re-estimated parame-
ters are fed back into the AV-HMM.
3.2 Audio-to-Visual Conversion
Hidden Markov Model Inversion (HMMI) was orig-
inally proposed in (Moon and Hwang, 1995) in the
context of robust speech recognition. Choi and co-
authors (Choi et al., 2001) used this technique to esti-
mate the visual features associated to audio features
for the purposes of speech driven facial animation.
Typically, it is assumed (Moon and Hwang, 1995),
(Choi et al., 2001), (Xie and Liu, 2007) a diagonal
structure for the covariance matrices of the Gaussian
mixtures, invoking reasons of computational com-
plexity. This assumption is relaxed in this paper al-
lowing for full covariance matrices. This leads to
more general expressions for the visual feature esti-
mates.
The idea of HMMI for audio-to-visual conver-
sion is to estimate the visual features based on the
trained AV-HMM, in such a way that the probabil-
ity that the whole audiovisual observation has been
generated by the model is maximized. It has been
proved (Baum and Sell, 1968) that this optimization
problem is equivalent to the maximization of the aux-
iliary function
Q(λ
av
;λ
av
,O
a
,O
v
,O
′
v
) ,
,
N
∑
j=1
M
∑
m=1
P(O
a
,O
v
, j,m | λ
av
) log P(O
a
,O
′
v
, j,m | λ
av
)
=
N
∑
j=1
M
∑
m=1
P(O
a
,O
v
, j,m | λ
av
)
"
log π
j
0
+
T
∑
t=1
log a
j
t−1
j
t
+
T
∑
t=1
log N (o
at
,o
′
vt
,µ
j
t
m
t
,Σ
j
t
m
t
) +
T
∑
t=1
log c
j
t
m
t
#
(3)
that is
O
′
v
= argmax
O
′
v
Q(λ
av
;λ
av
,O
a
,O
v
,O
′
v
)
(4)
where O
a
, O
v
and O
′
v
denote the matrices containing
the audio, visual and estimated visual sequences from
t = 1,...,T, respectively, π
j
0
denotes the initial prob-
ability for state j and a
j
t−1
j
t
denotes the state transi-
tion probability from state j
t−1
to state j
t
.
The solution to the optimization problem in (4)
can be computed by equating to zero the derivative of
Q with respect to o
′
vt
. Considering that the only term
that depends on o
′
vt
is the one involving the Gaussians,
this derivative can be written as
∂Q(λ
av
;λ
av
,O
a
,O
v
,O
′
v
)
∂o
′
vt
= 0
0 =
N
∑
j=1
M
∑
m=1
P(O
a
,O
v
, j, m | λ
av
) ×
×
∂
∂o
′
vt
"
T
∑
t=1
log N (o
at
,o
′
vt
,µ
j
t
m
t
,Σ
j
t
m
t
)
#
(5)
Considering that
log N (o
at
,o
′
vt
,µ
j
t
m
t
,Σ
j
t
m
t
) = log
1
(2π)
d/2
p
|Σ
j
t
m
t
|
−
−
1
2
o
at
− µ
a
j
t
m
t
o
vt
− µ
v
j
t
m
t
T
Φ
a
j
t
m
t
Φ
av
j
t
m
t
Φ
v
t
a
t
j
t
m
t
Φ
v
j
t
m
t
o
at
− µ
a
j
t
m
t
o
vt
− µ
v
j
t
m
t
(6)
where d is the dimension of o
avt
and
Σ
−1
j
t
m
t
=
Φ
a
j
t
m
t
Φ
av
j
t
m
t
Φ
va
j
t
m
t
Φ
v
j
t
m
t
,
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
170

the estimated visual observation becomes
o
′
vt
=
"
N
∑
j=1
M
∑
m=1
P(o
a
,o
v
, j,m | λ
av
)Φ
v
jm
#
−1
×
×
N
∑
j=1
M
∑
m=1
P(o
a
,o
v
, j,m | λ
av
)
h
Φ
v
jm
µ
v
jm
− Φ
va
jm
(o
at
− µ
a
jm
)
i
(7)
For the case of diagonal matrices, equation (7) re-
duces to
o
′
vt
=
"
N
∑
j=1
M
∑
m=1
P(o
a
,o
v
, j, m | λ
av
)Φ
v
jm
#
−1
×
×
N
∑
j=1
M
∑
m=1
P(o
a
,o
v
, j, m | λ
av
)Φ
v
jm
µ
v
jm
(8)
which is equivalent to the equation derived in (Choi
et al., 2001).
As is common in HMM training, the estimation
algorithms (7) and (8) are implemented in a recursive
way, initializing the visual observation randomly.
4 FEATURE EXTRACTION
The audio signal is partitioned in frames with the
same rate as the video frame rate. A number of
Mel-Cepstral Coefficients in each frame (a
t
) are used
in the audio part of the feature vector. To take
into account the audiovisual co-articulation, several
frames are used to form the audio feature vector o
at
=
a
T
t−t
c
,...,a
T
t−1
,a
T
t
,a
T
t+1
,...,a
T
t+t
c
T
corresponding to
the visual feature vector o
vt
.
For the visual part, the coefficients in an Indepen-
dent Component representation of the coordinates of
marks in the region around the mouth of the speaking
person are used, see Fig. 2(a). Let F = {f
1
,f
2
,...,f
T
}
represent the training data collected from videos.
Each vector f
t
= [x
(t)
1
,x
(t)
2
,...,x
(t)
P
,y
(t)
1
,y
(t)
2
,...,y
(t)
P
]
T
contains the coordinates (x
(t)
p
,y
(t)
p
) of each mark (p =
1,2,...,P) for the t-th frame, t = 1,2,...,T.
Let f
0
be the neutral facial expression, mainly de-
fined as the expression with all face muscles relaxed
and the mouth closed (ISO/IEC IS 14496-2, Visual,
1999), the relative facial deformation (with respect to
the neutral expression) at each frame can be computed
as d
t
= f
t
− f
0
, and a deformation matrix can then be
defined as
D = [d
1
,d
2
,...,d
T
] (9)
The different facial expressions in the training
data are represented by the columns of matrix D. The
idea is to represent any facial expression as the linear
combination of a reduced number of independentvec-
tors. The dimensionality reduction can be performed
by Principal Component Analysis (Hyv¨arinen et al.,
2001). The PCA stage yields an uncorrelated set of
vectors. It is desirable to have a statistically inde-
pendent set of vector so that information contained
in each vector will not provide information on any of
the others. This is the main idea in ICA. Summa-
rizing, ICA after PCA will be performed on the data
matrix D.
Several algorithms are available in the litera-
ture for ICA computation. The reader is referred
to (Hyv¨arinen et al., 2001) and the references therein.
In this paper, the symmetric decorrelation based Fast-
ICA algorithm as implemented in (G¨avertet al., 2005)
was employed.
As a result of the ICA processing, any facial de-
formation can then be computed as
f
t
=
K
∑
k=1
o
vt
k
u
k
+ f
0
(10)
where {u
k
}
K
k=1
are the independent components from
D and o
vt
k
is the k-th component of the visual vector
o
vt
. The coefficients o
vt
k
are computed in two stages.
In the first stage, the mark locations are estimated us-
ing image processing techniques. In the second stage,
the coefficients o
vt
k
are computed in such a way that
the facial expression is given by the linear combina-
tion of the ICs vectors that best match the mark es-
timation computed in the first stage. Details of this
procedure can be found in (Terissi and G´omez, 2007).
5 FACIAL ANIMATION
As already mentioned, the facial animation technique
proposed in this paper is MPEG-4 compliant. The
MPEG-4 standard defines 64 Facial Animation Para-
meters and 84 Feature Points (FPs) on a face model in
its neutral state (Ostermann, 2002). FAPs represent a
complete set of basic facial actions such as head mo-
tion, and eye, cheeks and mouth control. FPs are used
as reference points to perform the facial deformation.
Based on the estimated facial expression for each
frame, the associated FAPs can be determined by
computing the displacement of a set of marks from
their corresponding position in the neutral facial ex-
pression. For instance, the marks encircled in red in
Fig. 2(a) can be associated to FAP3 corresponding to
jaw opening. Figure 2(b) shows the resulting expres-
sion after applying the estimated FAP3 to the neutral
expression (several other FAPs, in addition to FAP3,
have also been applied to produce the mouth opening
HMM INVERSION WITH FULL AND DIAGONAL COVARIANCE MATRICES FOR AUDIO-TO-VISUAL
CONVERSION
171

(a) (b)
Figure 2: (a) Real person facial expression. Marks asso-
ciated to FAP3 are encircled in red. (b) Synthesized facial
expression.
and cheek movements). Similarly, several subsets of
marks can be associated to the different FAPs.
6 EXPERIMENTAL RESULTS
For the audio-visual training, videos of a talking per-
son with reference marks on the region around the
person’s mouth were recorded at a rate of 30 frames
per seconds, with a resolution of (320×240) pixels.
The audio was recorded at 11025Hz synchronized
with the video. The videos consist of sequences of the
Spanish utterances corresponding to the digits zero to
nine in random order. For the re-training of the audio
part of the AV-HMM, an only-audio database consist-
ing of recordings of sequences of the utterances cor-
responding to the digits zero to nine by 25 speakers
(balance proportion of males and females) was col-
lected.
Experiments were performed with AV-HMM with
full and diagonal covariance matrices, different num-
ber of states and mixtures in the ranges [3,20] and
[2,19], respectively, and different values of the co-
articulation parameter t
c
in the range [2, 5]. In the
experiments, the audio feature vector a
t
is composed
by the first eleven non-DC Mel-Cepstral coefficients,
while the visual feature vector o
v
is of dimension two
(K = 2 in equation (10)). The performances of the
different models were compared by computing the
Average Mean Square Error (AMSE)(ε), and the Av-
erage Correlation Coefficient (ACC)(ρ) between the
true and estimated visual parameters, defined as
ε =
1
TK
K
∑
k=1
1
σ
2
v
k
T
∑
t=1
o
′
vt
k
− o
vt
k
2
(11)
ρ =
1
TK
T
∑
t=1
K
∑
k=1
(o
vt
k
− µ
v
k
)(o
′
vt
k
− µ
′
v
k
)
σ
v
k
σ
′
v
k
(12)
respectively, where µ
v
k
and σ
v
k
denote the mean and
the variance of the true visual observation, respec-
tively, and µ
′
v
k
and σ
′
v
k
denote the mean and variance
of the estimated visual parameters, respectively.
For the quantification of the visual estimation ac-
curacy, a separate audio-visual dataset, different from
the training dataset, was employed. The following re-
sults correspond to a co-articulation parameter t
c
= 5,
which proves to be the optimal value in the given
range. Fig. 3(a) and Fig. 3(b), show the AMSE and
the ACC as a function of the number of states and the
number of mixtures for an AV-HMM with full covari-
ance matrix. In this case, equation (7) applies for the
estimation of the visual observations o
′
vt
. As can be
observed, as the number of states and the number of
mixtures increase, the AMSE increases and the ACC
decreases, indicating that the accuracy of the estima-
tion deteriorates. This is probably due to the bias-
variance tradeoff inherent to any estimation problem.
The optimal values for the number of the states and
mixtures would be for this case N = 4 and M = 2,
respectively, corresponding to ε = 0.47 and ρ = 0.75.
Fig. 3(c) and Fig. 3(d), show the AMSE and the
ACC as a function of the number of states and the
number of mixtures for an AV-HMM with diagonal
covariance matrix. In this case, equation (8) applies
for the estimation of the visual observations o
′
vt
. As
can be observed, to obtain a similar accuracy a more
complex model (larger number of states or mixtures)
is required. For this case, the optimal values are N =
19 and M = 3, corresponding to ε = 0.47 and ρ =
0.76.
The use of full covariance matrices affects the
computational complexity during the training stage
but, since this is carried out off-line, this does not rep-
resent a problem. During the synthesis stage (visual
estimation through HMM inversion), and due to the
low dimension of the visual feature vector (K = 2),
the computational load is similar to the case of using
diagonal covariance matrices for the same number of
states and mixtures.
The above arguments allow one to conclude that
the use of full covariance matrices is preferable from
the point of view of both computational complexity
and accuracy.
The true and estimated visual parameters for the
case of full covariance matrices with N = 4 states and
M = 2 mixtures (optimal values) are represented in
Fig. 4, where a good agrement can be observed.
7 CONCLUSIONS
A speech driven MPEG-4 compliant facial animation
system was introduced in this paper. A joint AV-
HMM is proposed to represent the audio-visual data
and an algorithm for HMM inversion was derived for
the general case of considering full covariance matri-
SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications
172

3 5 7 9 11 13 15 17 19 21
0.4
0.5
0.6
0.7
0.8
0.9
2
3
7
19
ε
N
M
(a)
3 5 7 9 11 13 15 17 19 21
0.55
0.6
0.65
0.7
0.75
0.8
2
3
7
19
N
M
ρ
(b)
3 5 7 9 11 13 15 17 19 21
0.4
0.5
0.6
0.7
0.8
0.9
2
3
7
19
ε
N
M
(c)
3 5 7 9 11 13 15 17 19 21
0.55
0.6
0.65
0.7
0.75
0.8
2
3
7
19
N
M
ρ
(d)
Figure 3: AMSE (ε) and ACC (ρ) as a function of the num-
ber of states N and the number of mixtures M. Where (a)
and (b) correspond to the case of full covariance matrices
and, (c) and (d) correspond to the case of diagonal covari-
ance matrices.
20 40 60 80 100 120 140 160 180 200
-5
-2.5
0
2.5
5
7.5
10
# Frames
o
v
1
o
′
v
1
o
v
2
o
′
v
2
Figure 4: True (dashed line) and estimated (solid line) vi-
sual observations.
ces for the audio-visual observations. The influence
on the visual estimation accuracy of the use of full
covariancematrices, as opposed to diagonal ones, was
investigated. Simulation results show that the use of
full covariance matrices leads to an accurate estima-
tion of the visual parameters, yielding the same per-
formance as with diagonal covariance matrices, but
with a less complex model and without affecting sig-
nificantly the computational load.
REFERENCES
Baum, L. E. and Sell, G. R. (1968). Growth functions
for transformations on manifolds. Pacific Journal of
Mathematics, 27(2):211–227.
Brand, M. (1999). Voice puppetry. In Proceedings of SIG-
GRAPH, pages 21–28, Los Angeles, CA USA.
Chen, T. (2001). Audiovisual speech processing. IEEE Sig-
nal Processing Magazine, 18(1):9–21.
Choi, K., Luo, Y., and Hwang, J. (2001). Hidden Markov
Model inversion for audio-to-visual conversion in an
MPEG-4 facial animation system. Journal of VLSI
Signal Processing, 29(1-2):51–61.
Fu, S., Gutierrez-Osuna, R., Esposito, A., Kakumanu, P.,
and Garcia, O. (2005). Audio/visual mapping with
cross-modal Hidden Markov Models. IEEE Trans. on
Multimedia, 7(2):243–252.
G¨avert, H., Hurri, J., S¨arel¨a, J., and Hyv¨arinen, A.. FastICA
package for MATLAB. Lab. of Computer and Infor-
mation Science, Helsinki University of Technology.
Hyv¨arinen, A., Karhunen, J., and Oja, E. (2001). Indepen-
dent Component Analysis. John Wiley & Sons, Inc.,
New York.
ISO/IEC IS 14496-2, Visual (1999).
Moon, S. and Hwang, J. (1995). Noisy speech recogni-
tion using robust inversion of Hidden Markov Models.
In Proceedings of IEEE International Conf. Acoust.,
Speech, Signal Processing, pages 145–148.
Ostermann, J. (2002). MPEG-4 Facial Animation - The
Standard, Implementation and Applications, chapter
Face Animation in MPEG-4, pages 17–56. John Wi-
ley & Sons.
Rao, R., Chen, T., and Mersereau, R. (1998). Audio-
to-visual conversion for multimedia communication.
IEEE Trans. on Industrial Electronics, 45(1):15–22.
Terissi, L. D. and G´omez, J. C. (2007). Facial motion track-
ing and animation: An ICA-based approach. In Pro-
ceedings of 15th European Signal Processing Confer-
ence, pages 292–296, Pozna´n, Poland.
Viterbi, A. J. (1967). Error bounds for convolutional codes
and an asymptotically optimal decoding algorithm.
IEEE Trans. on Information Theories, 13:260–269.
Xie, L. and Liu, Z.-Q. (2007). A coupled HMM approach to
video-realistic speech animation. Pattern Recognition,
40:2325–2340.
Yamamoto, E., Nakamura, S., and Shikano, K. (1998).
Lip movement synthesis from speech based on Hid-
den Markov Models. Speech Communication, 26(1-
2):105–115.
HMM INVERSION WITH FULL AND DIAGONAL COVARIANCE MATRICES FOR AUDIO-TO-VISUAL
CONVERSION
173
