ACCURATE AUTOMATIC SPOT ADDRESSING FOR MICROARRAY

IMAGES

M´onica G. Larese and Juan C. G´omez

Lab. for System Dynamics and Signal Processing, FCEIA, UNR

CIFASIS, CONICET, Bv. 27 de Febrero 210 Bis, Rosario, Argentina

Keywords:

Bioinformatics, cDNA microarrays, image analysis, automatic addressing.

Abstract:

In this paper a novel procedure based on texture spatial characterization techniques is proposed aimed at

automatically addressing spots in microarray images. The algorithm relies on the regular and pseudo-periodic

patterns of spots, which can be considered as texture primitives. A fully automatic procedure is proposed to

segment the autocorrelation functions of subgrid images and accurately determine the locations of the peaks.

These candidate peaks, i.e., vectors, are next used to compute the displacement vectors that fully characterize

the spatial arrangement of spots, describing the spot spacing and angle of rotation of the pattern. A reﬁnement

procedure is then applied to improve the accuracy of the norms and angles of the displacement vectors. An

ideal template is generated using the computed spanning vectors, which is deformed and adjusted via Markov

Random Fields (MRF) modelling. Experiments based on artiﬁcial and real images are promising, showing

improvements regarding robustness against image rotations, and accuracy, over results provided by state-of-

the-art methods.

1 INTRODUCTION

A fundamental step in microarray image analysis is

the addressing of spots within image subgrids, in or-

der to measure the hybridization levels. Even though

spots are regularly located, this task is difﬁcult due to

the low quality of the images. Current methods aimed

at addressing spots include semiautomatic (Heyer

et al., 2005; Yang et al., 2000; Eisen, 1999) and au-

tomatic (Ceccarelli and Antoniol, 2006; Hartelius and

Carstensen, 2003; Jain et al., 2002) procedures.

In this paper a new approach based on tech-

niques from texture spatial characterization is pro-

posed, where spots are considered as the texture prim-

itives. An autocorrelation segmentation procedure is

introduced in order to accurately estimate the two

displacement vectors which completely characterize

the lattice. After a reﬁnement procedure, these vec-

tors deﬁne an ideal regular lattice which is ﬁnally de-

formed and adjusted using MRFs.

2 METHODOLOGY

2.1 Autocorrelation Segmentation

Autocorrelation was proposed for regular texture

structure characterization on general purpose images

in (Lin et al., 1997) and then applied with slight vari-

ations in (Liu et al., 2004). However, both procedures

lead to discrete displacement vectors, propagating the

errors to the estimated lattice of texture primitives.

In the present paper, a new approach is presented

to extract the spanning vectors using subpixel preci-

sion. In order to do this, the following operations are

applied on the autocorrelation image computed from

the microarray subgrid image:

1. Edge Detection via a LoG

ﬁlter and zero-

crossings detection (Gonzalez and Woods, 2002).

2. Morphological Reconstruction to ﬁll holes in-

side object boundaries. After this step, two dif-

ferent cases may occur, viz., either separated or

non-separated connected components.

If the components are separated, skip step 3, oth-

erwise:

LoG: Laplacian of Gaussian

221

G. Larese M. and C. Gómez J. (2008).

ACCURATE AUTOMATIC SPOT ADDRESSING FOR MICROARRAY IMAGES.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 221-224

DOI: 10.5220/0001941202210224

 SciTePress

3. Morphological Binary Opening trying circular

structuring elements with incremental radii, until

all the components are separated.

4. Connected Components Labelling.

5. Deletion of the components touching the border.

6. The Centroid Coordinates of each component

are regarded as the location of the candidate

peaks.

2.2 Displacement Vectors Calculation

The approach based on regions of dominance pro-

posed in (Liu et al., 2004) is applied to the centroids

computed in Section 2.1 in order to determine the

most prominent candidate peaks (regarded as vectors)

to be considered in the displacement vectors compu-

tation. Next, the procedure described in (Lin et al.,

1997), which is based on the generalized Hough trans-

form, is implemented in order to ﬁnd the two vectors

that generate the spot lattice.

2.3 Spot Spacing and Angle of Rotation

Reﬁnement

The norms of the two spanning vectors describe the

spot row and column spacings. Their angle describe

the deviation in each axis direction. In order to im-

prove accuracy even more, a histogram with the sizes

of the regions of dominance for all the candidate vec-

tors is constructed, as well as a histogram of the cor-

responding angles. The norms and angles of the two

displacement vectors computed in the previous Sec-

tion are used as entries to each one of these his-

tograms, and the weighted mean of the corresponding

isolated region in each histogram is regarded as the

corrected norm and angle for each spanning vector.

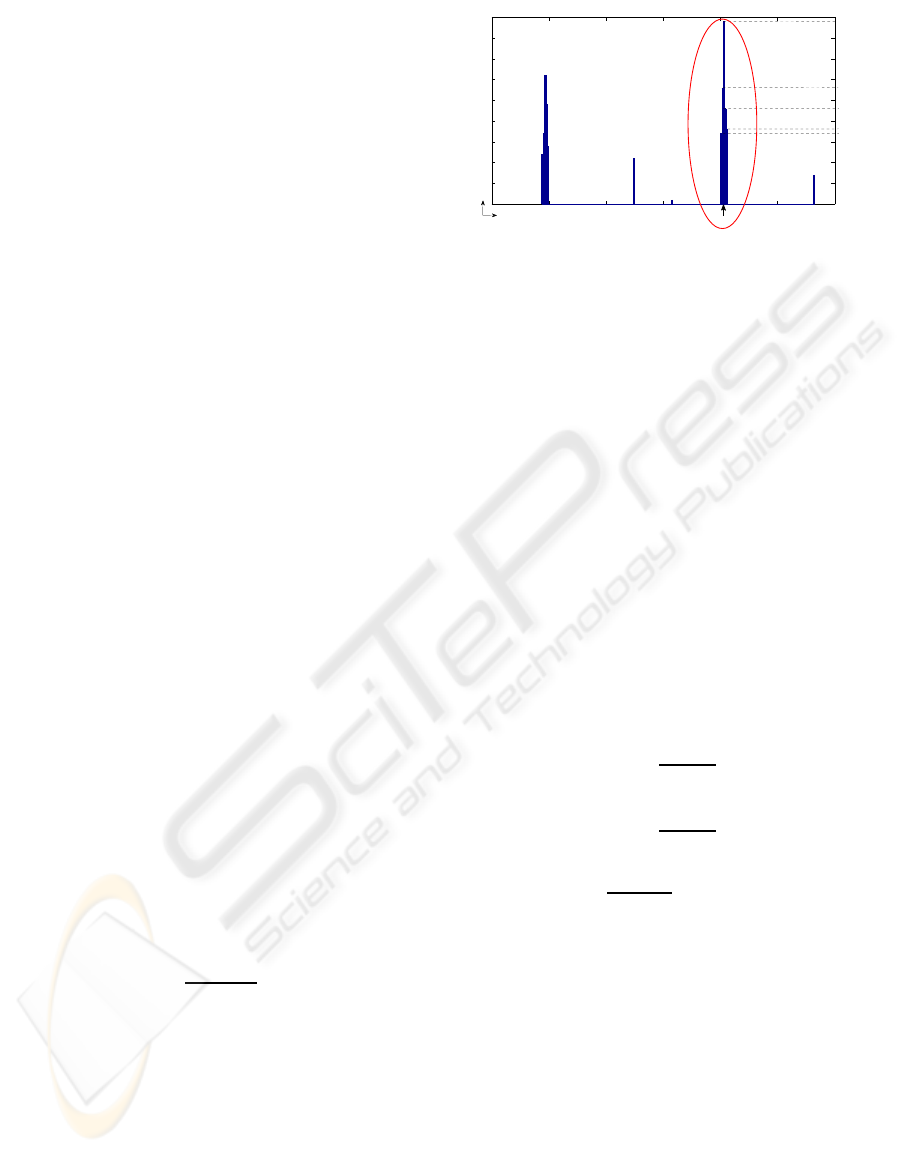
The procedure is illustrated in Fig. 1, where the

sizes of the regions of dominance (angles) histogram

is depicted. The corrected norm (angle) ∆

for each

one of the two spanning vectors is computed as

∆

∑

i=1

∆

∑

i=1

(1)

where f

and ∆

, i = 1, . . . , n stand for the frequencies,

and sizes of the regions of dominance (angles), re-

spectively. In the ﬁgure, ∆

′

represents the norm (an-

gle) computed in the previous Section for each one of

the displacement vectors (n = 5 in the example).

2.4 Template Adjustment via MRFs

A template grid can be constructed using the two pre-

viously estimated displacement vectors. The number

−2 −1.5 −1 −0.5 0 0.5 1

∆

′

Figure 1: Illustration of the procedure for spots spacing and

angle of rotation reﬁnement.

of rows, N

, and columns, N

, of spots are known a

priori from the microarrayer conﬁguration. In order

to determine the starting position to span the template,

the top-leftmost spot of the real subgrid is determined

using the horizontal and vertical proﬁles of the tem-

porarily corrected for rotation image.

A ﬁrst-order MRF (Geman and Geman, 1984) is

used to model the lattice of spots, allowing their lo-

cations to stochastically deviate from the ideal tem-

plate. The label set L = {l

= (x

, y

), i = 1, ..., N

}

contains the pairs of spatial coordinates for each node

site i, i.e., spot center, in the template.

The deﬁnition of an energy functional is heuris-

tic and application dependent, and theoretical ways of

determining it are not established yet (Amador J. J.,

2005). In this paper, the MRF functional to be mini-

mized was deﬁned as

MRF

= E

lat

+ E

homog

(2)

lat

= α

∑

i∼ j



(i, j)



+ α

∑

i∼ j



(i, j)

− 1



− α

(i) (3)

homog

= β

µ(i)

σ(i) + 1

(4)

The term E

lat

controls the distortion of the grid. In

Eq. (3), d

(i, j) is the deviation in alignment between

neighboring nodes i and j, whereas d

(i, j) − D is the

deviation from the ideal ﬁxed spot spacings D be-

tween i and j, as proposed by Carstensen (Carstensen

J. M., 1996).

On the other hand, d

(i) adopts one of two pos-

sible values: 0 or 1. In order to determine the d

(i)

value, the centroids of all the connected components

of the original microarray subgrid are computed. The

function d

(i) is then deﬁned as follows

(i) =

(

1 if (x

, y

) coincides with a centroid

0 otherwise

(5)

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

222

a. b.

Figure 2: Results of addressing a simulated image for the: a.) Proposed algorithm. b.) UCSF-Spot algorithm.

The term E

homog

measures the local intensity ho-

mogeneity around site i. For spot centers it is desir-

able to lie in homogeneous regions, such as the center

region of a spot. It is undesirable for them to lie on

borders. The local intensity mean value µ(i) and local

standard deviation σ(i) is computed on the 7x7 pixels

(not sites!) neighborhood of node site i.

The parameters α

, α1, α

and β are weights that

control the contribution of each term. In this work,

their values were experimentally set to 1, 10, 1000,

and 0.3, respectively. Minimization of the energy

functional was carried out using simulated annealing,

with an initial temperature of 0.8 and 1000 iterations.

3 EXPERIMENTAL RESULTS

In order to validate the proposed algorithm, experi-

ments on synthetic and real microarray images were

performed. Accuracy was assessed by means of

the RMSE (root-mean-square-error) between the es-

timated spot locations and the real ones.

3.1 Computer Generated Images

Two types of experiments were performed using syn-

thetic images. In the ﬁrst case, subgrids with spot row

spacing different from column spacing, and random

spot sizes, were analyzed with the proposed method

and the UCSF-Spot automatic algorithm (Jain et al.,

2002). The results are shown in Figures 2(a) and (b),

respectively. As can be observed from Fig. 2(b) the

UCSF-Spot algorithm fails to address the spots, try-

ing to unify the row and column spacings. On the

other side, the proposed algorithm succeeds in locat-

ing the spots, as shown in Fig. 2(a), where the blue

crosses indicate the estimated spot centers.

In the second set of experiments, subgrids were

generated with equal row and column spacings, but

the locations of spots were randomly altered from

the regular lattice with Gaussian distributed variations

with zero mean and variances 0, 4 and 9. The images

were rotated with angles in the range [−5, 5] degrees

= 0

= 4

= 9

Angle (in degrees)

Total RMSE (in pixels)

-2 -1

-1.5 -0.5 0.5 1.5

Figure 3: RMSE for the proposed and UCSF-Spot algo-

rithms (solid and dash-dotted lines, respectively) as a func-

tion of the image rotation angle.

and then analyzed with the proposed method and the

UCSF-Spot algorithm.

In Fig. 3 the RMSE for the proposed (solid line)

and UCSF-Spot (dash-dotted line) algorithms as a

function of the image rotation angle is depicted for

spot location variances equal to 0 (circles), 4 (squares)

and 9 (triangles). As it can be observed, the algo-

rithm introduced in this paper outperforms the UCSF-

Spot algorithm. In addition, it can be noticed that the

RMSE of the UCSF-Spot algorithm increases consid-

erably for rotation angles greater than 2 degrees, lead-

ing to unacceptable results.

In all the cases, the RMSE curve corresponding to

the proposed method is below 5 pixels, and below the

respective RMSE curves of UCSF-Spot.

3.2 Real Microarray Images

The proposed method was compared to the UCSF-

Spot algorithm and the accuracy of each method was

measured through the RMSE calculation on typical

real microarray images collected from the Standford

Microarray Database (SMD) (Demeter et al., 2007).

Details about the images, RMSEs in the x and y di-

rections and total RMSEs are reported in Table 1.

In all the cases under analysis, the proposed method

obtained a lower RMSE when compared to UCSF-

Spot. It is also worth noticing that (Ceccarelli and

ACCURATE AUTOMATIC SPOT ADDRESSING FOR MICROARRAY IMAGES

223

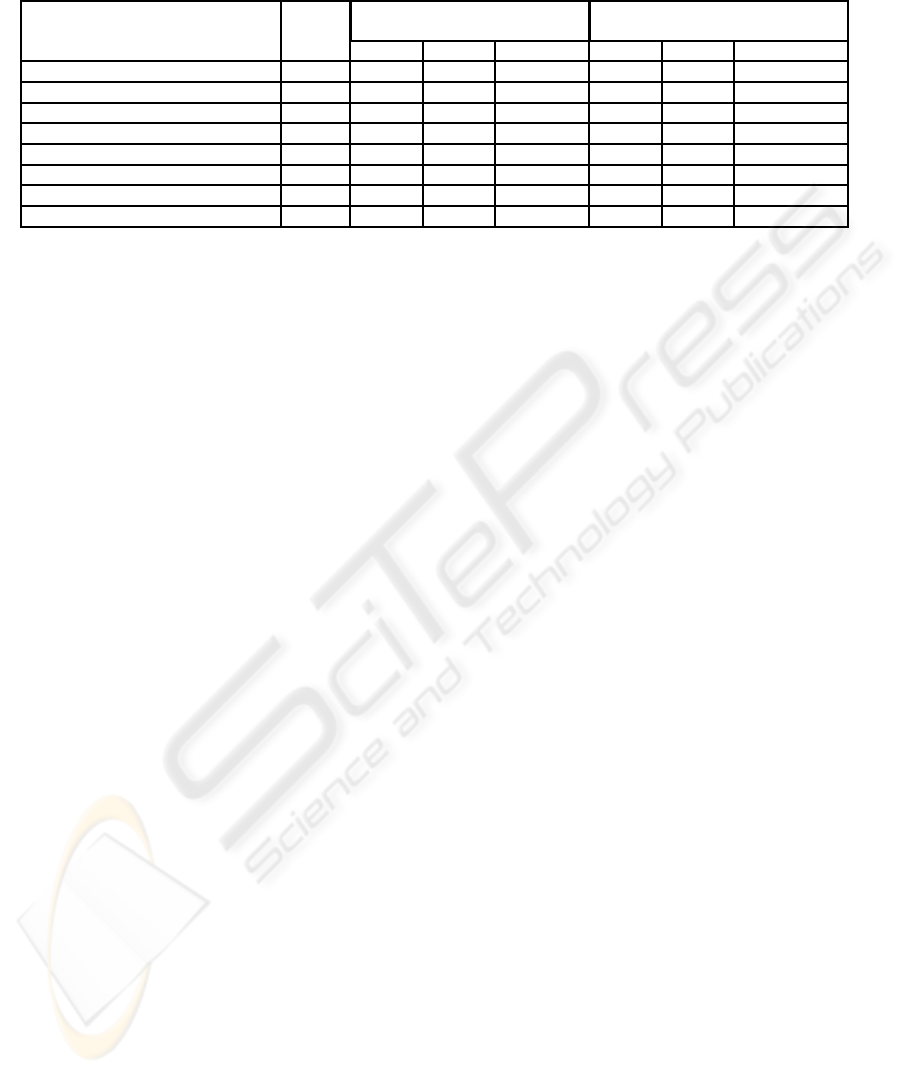
Table 1: Accuracy of spot addressing in terms of the RMSE (in pixels) for the proposed automatic algorithm and the UCSF-

Spot algorithm described in (Jain et al., 2002).

Image ID # spots

RMSE for the RMSE for

proposed method UCSF-Spot

RMSE

Total RMSE RMSE

RMSE

Total RMSE

lc7b070rex2 (Alizadeh et al., 2000) 9216 1.56 1.52 2.18 44.21 4.97 44.49

lc7b017rex2 (Alizadeh et al., 2000) 9216 1.04 1.88 2.15 66.89 10.80 67.75

lc7b0104rex2 (Alizadeh et al., 2000) 9216 0.95 1.38 1.68 70.23 8.67 70.76

21028 (Subramanian et al., 2005) 43008 1.14 1.45 1.85 49.12 1.53 49.14

16275 (Subramanian et al., 2005) 45312 1.93 2.00 2.78 10.40 11.90 15.80

43957 (Subramanian et al., 2005) 43008 1.14 1.45 1.85 3.40 1.90 3.89

41602 (Subramanian et al., 2005) 43008 1.19 1.28 1.75 6.42 10.57 12.36

15739 (Arbeitman et al., 2002) 9216 1.76 1.66 2.42 7.67 6.45 10.02

Antoniol, 2006) also tested their method on images

21028, 16275, 43957, 41602 and 15739 reporting

higher RMSEs than the ones obtained by the method

proposed in this paper (image ID 51509 could not

be tested because it is no longer available for down-

load from SMD). The whole algorithm takes approx-

imately 15 seconds for a typical subgrid like this on a

1.6 GHz AMD-64 under Matlab and Linux, including

I/O operations.

4 CONCLUSIONS

In this paper an automatic approach is proposed to

address the location of microarray subgrid spot cen-

ters. The method relies on the assumption that spotted

microarray images can be regarded as regular texture

images and consequently texture spatial characteriza-

tion techniques are suitable to be applied. This is due

to the regularity and pseudo-periodicity exhibited by

microarray images.

Experimental results on synthetic and real images

show that the proposed method outperforms the ones

provided by a state-of-the-art microarray analysis tool

(namely the UCSF-Spot) especially when large im-

age rotations and unequal row and column spacings

are present. The present authors believe that the

method yields promising results improving accuracy

over widely used tools available in the literature.

REFERENCES

Alizadeh, A. A., Eisen, M. B. et al (2000). Distinct types

of diffuse large B-cell lymphoma identiﬁed by gene

expression proﬁling. Nature, 403(6769):503–511.

Amador J. J. (2005). Markov random ﬁeld approach to re-

gion extraction using tabu search. J. Vis. Commun.

Image R., 16:134–158.

Arbeitman, M. N. et al (2002). Gene expression during

the life cycle of Drosophila melanogaster. Science,

297:2270–2275.

Carstensen J. M. (1996). An active lattice model in a

Bayesian framework. Comput. Vis. Image Und.,

63(2):380–387.

Ceccarelli, M. and Antoniol, G. (2006). A deformable

grid-matching approach for microarray images. IEEE

Trans. Image Proc., 15(10):3178–3188.

Demeter, J., Beauheim, C. et al (2007). The Stanford Mi-

croarray Database: implementation of new analysis

tools and open source release of software. Nucleic

Acids Res., 35(Database Issue):D766–770.

Eisen, M. (1999). Scanalyze. http://rana.lbl.gov/EisenSoft-

ware.html.

Geman, S. and Geman, D. (1984). Stochastic relaxation,

gibbs distributions and the bayesian restoration of im-

ages. IEEE Trans. P.A.M.I., 6:721–741.

Gonzalez, R. and Woods, R. (2002). Digital image process-

ing. Prentice Hall, 2nd. edition.

Hartelius, K. and Carstensen, J. M. (2003). Bayesian grid

matching. IEEE Trans. P.A.M.I., 25(2):162–173.

Heyer, L. J., Moskowitz, D. Z. et al (2005). Magic tool:

integrated microarray data analysis. Bioinformatics,

21(9):2114–2115.

Jain, A. N., Tokuyasu, T. A. et al (2002). Fully automatic

quantiﬁcation of microarray image data. Genome Re-

search, 12:325–332.

Lin, H.-C., Wang, L.-L., and Yang, S.-N. (1997). Extracting

periodicity of a regular texture based on autocorrela-

tion functions. Pat. Recognition Letters, 18:433–443.

Liu, Y., Collins, R. T., and Tsin, Y. (2004). A computa-

tional model for periodic pattern perception based on

frieze and wallpaper groups. IEEE Trans. P.A.M.I.,

26(3):354–371.

Subramanian, S., West, R. B. et al (2005). The gene expres-

sion proﬁle of extraskeletal myxoid chondrosarcoma.

J. Pathol., 206:433–444.

Yang, Y., Buckley, M. et al (2000). Comparison of

methods for image analysis on cDNA microarray

data. Tech. Report #584, Dep. of Stat., UCB. URL:

http://www.stat.berkeley.edu/users/terry/zarray/Tech-

Report/584.pdf.

SIGMAP 2008 - International Conference on Signal Processing and Multimedia Applications

224