
ON THE PRACTICAL PERFORMANCE OF RATELESS CODES
∗
Miroslav Kneˇzevi´c, Vesselin Velichkov, Bart Preneel and Ingrid Verbauwhede
K.U. Leuven, ESAT/COSIC and IBBT
Kasteelpark Arenberg 10, B-3001 Leuven-Heverlee, Belgium
Keywords:
Coding, error-correction codes, rateless codes, online codes.
Abstract:
We propose a new parameter for optimizing the performance of rateless codes by minimizing latency and data
overhead. We call it Latency-Overhead Product (LOP). It is based on ideas used in the analysis of digital
circuits. We demonstrate the effectiveness of the LOP parameter for a specific class of rateless codes called
Online codes (OC). We give results from experiments in ideal channel and simulated wireless channel with
losses. In the second part of our experiments we analyze the relationship between the message block size
and the performance of rateless codes. With the results from these experiments we extend the results from
the performance of Luby Transform (LT) codes published in (Vukobratovic and Despotovic, 2005) by adding
figures for Online codes.
1 INTRODUCTION
Rateless codes (RC) (Luby et al., 2001; Luby, 2002;
Maymounkov, 2002; Shokrollahi, 2006; MacKay,
2005) are a class of error correction codes, used for
encodingdata transmitted over channels with variable
packet error rate. An example of such a channel is
a wireless link. Due to the fading effect present in
wireless channels, the capacity of the latter is not con-
stant. Non-constant channel capacity results in vary-
ing packet error rate. Although rateless codes are well
suited for channels with varying error rate, their use
often causes data overhead and delays. Minimizing
both data overhead and delay is critical for achiev-
ing optimal performance of rateless codes. In the pre-
sented research, we address the mentioned problem
for the case of rateless codes. We support our con-
clusions with experimental results for a specific class
of rateless codes called Online codes (Maymounkov,
2002).
∗
This work is funded partially by IBBT, Katholieke Uni-
versiteit Leuven (OT/06/40) and FWO projects (G.0300.07
and G.0450.04). This work was supported in part by
the IAP Programme P6/26 BCRYPT of the Belgian State
(Belgian Science Policy), by the EU IST FP6 projects
(ECRYPT) and by the IBBT-QoE project of the IBBT.
2 OUR CONTRIBUTION
We propose a new parameter - Latency-Overhead
Product (LOP) for evaluating and optimizing the per-
formance of rateless codes. We use the proposed pa-
rameter to experimentally find the optimal number of
the blocks into which a message should be divided
prior to being encoded with rateless codes. We evalu-
ate the optimal block size in terms of latency and data
overhead.
3 LATENCY-OVERHEAD
PRODUCT
The proposed metric - Latency-Overhead Product
(LOP) is inspired by ideas used in the analysis of dig-
ital circuits. In digital circuits theory there exists the
so called parameter Area-Delay Product (ADP). ADP
is widely used as a measure for evaluating the optimal
performanceof the integrated circuit in terms of mini-
mum delay and consumed area. Analogously to ADP,
we propose the Latency-OverheadProduct (LOP) as a
measure for evaluating the optimal number of blocks
into which a message should be broken prior to be-
ing encoded with rateless codes. LOP evaluates op-
timality in terms of minimum latency and minimum
overhead.
173
Kneževi
´
c M., Velichkov V., Preneel B. and Verbauwhede I. (2008).
ON THE PRACTICAL PERFORMANCE OF RATELESS CODES.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 173-176
DOI: 10.5220/0002021801730176
Copyright
c
SciTePress

4 LOP AND RATELESS CODES
Let us consider an encoder for a file of size n blocks.
Let δ be the average overhead and t
d
total decoding
time of the algorithm. We define Latency-Overhead
Product as:
LOP = LOP(n) = δ
α
t
β
d
(1)
where α and β are weight parameters of the LOP
function. By fixing the weights α and β to specific
values we are choosing whether the LOP minimiza-
tion will be done with a stronger preference for small
overhead (α > β) or small delay (α < β). For exam-
ple if we are more interested in having small overhead
rather than small delay (i.e. we want the delay also to
be small, but this is not as important as having a small
overhead) then we can indicate this by giving a larger
weight value for α and smaller weight value for β e.g.
α = 2, β = 1. The resultant value for the LOP function
is LOP = δ
2
t
d
.
In general, the overhead δ and latency t
d
are func-
tions of several parameters. In realistic environments
they depend on the state of the channel. For a very
general case we can derive a theoretical condition that
needs to be fulfilled in order to obtain optimal value
for the block size n for a given rateless code:
∂LOP
∂n
= αδ
α−1
t
β
d
∂δ
∂n
+ βt
β−1
d
δ
α
∂t
d
∂n
= 0 . (2)
In other words, given the parameters α and β, using
LOP we can find an optimal n such that Eq. (3) holds.
α
δ
∂δ
∂n
= −
β
t
d
∂t
d
∂n
. (3)
Here δ and t
d
depend on the type of rateless code that
is used and on the state of the channel. If Eq. (3) has
a real solution we can achieve an optimal value for n.
We show the effectiveness of the LOP in prac-
tice for a specific class of rateless codes called Online
codes. Before presentingour experimentalresults, we
give a short description of Online codes.
5 ONLINE CODES
Online codes (OC) are a type of rateless codes suit-
able for channels with an unknown or variable loss
rate. OC were introduced by Petar Maymounkov
in (Maymounkov, 2002). They are efficient error-
correction codes, requiring O(1) time to generate
each encoding block and O(n) time to decode an orig-
inal message of length n. Detailed treatment of On-
line codes is given in (Maymounkov,2002)and (May-
mounkov and Mazieres, 2003).
Table 1: Calculating the Optimal Block Size using LOP pa-
rameter - Ideal Channel.
Message size Overhead Latency LOP
n [%] [s] [ms]
667 31.23 0.22 21.46
833 28.36 0.23 18.50
1,333 21.38 0.26 11.88
2,000 16.93 0.30 8.60
4,000 8.21 0.55 3.71
10,000 5.32 1.26 3.57
12,000 5.00 1.82 4.59
20,000 4.76 3.92 8.88
40,000 4.05 12.52 20.54
In our experiments we use LOP to measure the
optimal number of message blocks when message is
encoded with Online codes in two cases: ideal chan-
nel and simulated wireless channel with losses. We
simulate a channel with losses with a Gilbert-Elliot
model. Next we describe our experimental settings
and provide the obtained results.
6 EXPERIMENTS AND RESULTS
In order to show the usefulness of the pro-
posed parameter LOP we have implemented Online
codes (Maymounkov, 2002).
2
. With Online codes we
conduct two sets of experiments: (1) finding an op-
timal block size with LOP; (2) measuring the gen-
eral performance of Online codes in respect to packet
size vs. total overhead. The first experiment is con-
ducted for two cases: (a) ideal channel (b) channel
with losses, simulated according to a Gilbert-Elliot
model.
6.1 Optimal Block Size with Lop
In this set of experimentswe use LOP in order to eval-
uate the optimal blocksize of a message encoded with
OC. We run 10, 000 simulations per measurement.
One simulation consists of encoding and decoding of
a test file, using Online codes. In all simulations we
use a test file of size 1 MB. During experiments we
change the size of the blocks into which the test file is
broken, resp. we change the number of blocks com-
posing the file. In each simulation we measure the
two parameters of the LOP function: (1) Overhead δ
- the difference between the number of original mes-
sage blocks n and the total number of sent message
2
The source code for our Online codes imple-
mentation is licensed under GPL and is available at
http://sourceforge.net/projects/onlinecodes
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
174
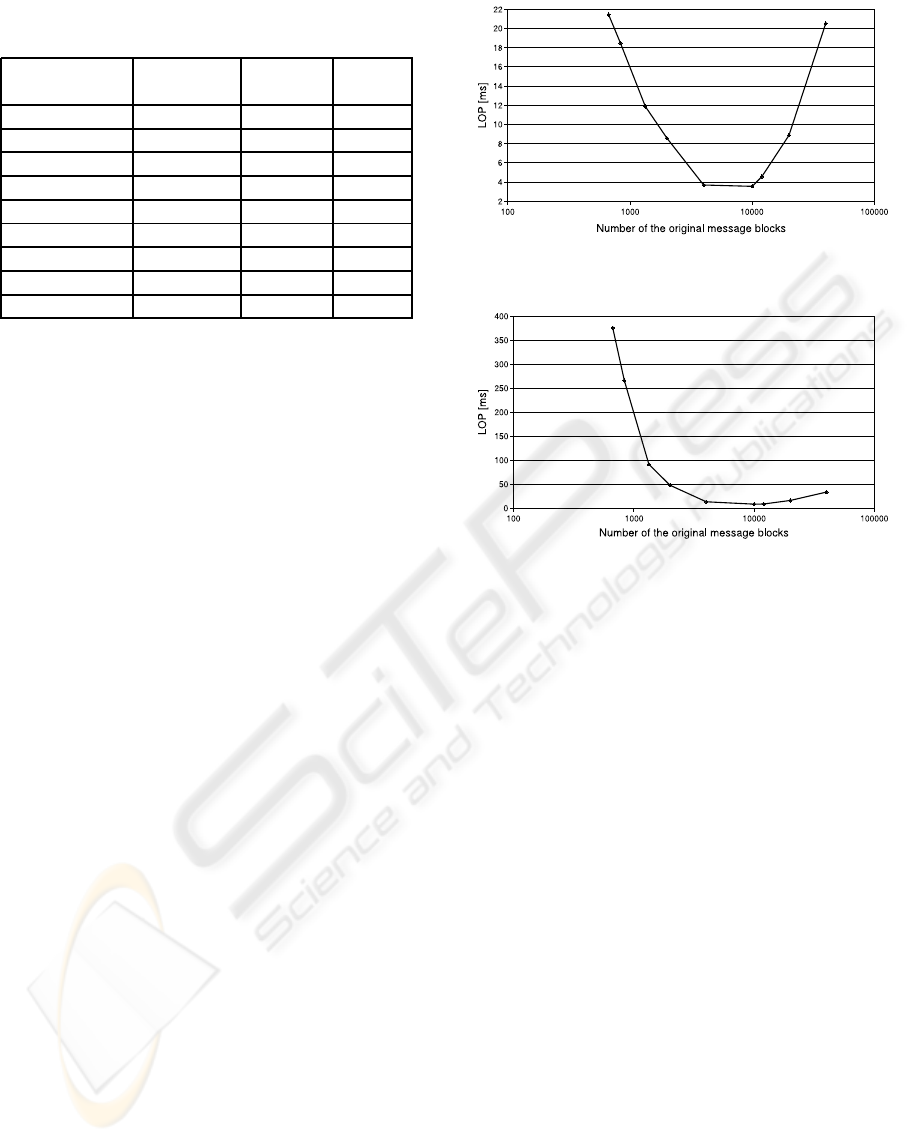
Table 2: Calculating the Optimal Block Size using LOP pa-
rameter - Wireless Channel.
Message size Overhead Latency LOP
n [%] [s] [ms]
667 49.55 1.53 375.65
833 42.10 1.50 256.86
1,333 30.37 0.99 91.31
2,000 22.85 0.91 47.51
4,000 10.61 1.17 13.17
10,000 6.23 2.11 8.19
12,000 5.88 2.47 8.54
20,000 5.32 5.63 15.95
40,000 4.79 14.55 33.38
blocks necessary for successful decoding and (2) La-
tency t
d
- the total time measured from start of the
encoding until the end of decoding.
In Tables 1 and 2 are shown results from calculat-
ing LOP for the cases of ideal channel and channel
with losses respectively. In each simulation we calcu-
late the value of the LOP function, using the measured
values for δ and t
d
. For our test settings, we give pref-
erence to minimizing the packet overhead over min-
imizing the computational costs. That results in the
values α = 2, β = 1 for the weight parameters of the
LOP function.
From Tables 1 and 2 we can see that for ideal
channel the minimum value of the LOP parameter
is 3.57 ms and for channel with losses this value is
equal to 8.19 ms. Both values are obtained for the
case when the original message is broken down to
10, 000 blocks. The encoding and decoding of this
message, using Online codes results in 1.26 s latency
and 5.32 % overhead for ideal and 2.11 s latency and
6.23 % overhead for channel with losses respectively.
These values are optimalunderthe setup conditionsof
the experiment (globalparameters ofthe Online codes
algorithm and LOP constants - α and β).
The data from Tables 1 and 2 is used to con-
struct the graphs in Figs. 1 and 2 respectively. The
two graphs represent the values of Latency-Overhead
Product as a function of the message size n.
6.2 Packet Size Vs. Total Overhead
In this set of experiments we investigate the relation-
ship between the packet size and the total overhead
when transmitting a test file encoded with Online
codes. We transmit a file of size 1M Byte using blocks
of different size varying from 25 Bytes to 500 Bytes.
This causes the number of blocks in which the origi-
nal file is broken to vary from 40, 000 to 2, 000 blocks
respectively. The test file is transmitted over the sim-
Figure 1: LOP as a function of the message size - Ideal
Channel.
Figure 2: LOP as a function of the message size - Wireless
Channel.
ulated wireless channel. The channel is simulated ac-
cording to the Gilbert-Elliot model where packet error
rate is packet length dependent.
The results from this test are presented in four
graphs in Fig. 3. We have one graph for each block
size. Each graph represents a histogram showing
the total number of experiments (ordinate) where the
overhead has a specific value (abscissa). White bars
represent the overhead on the transmitting side and
are more interesting for us. They show the total over-
head of the transmitting file. The black bars give
just an overhead at the receiving side. Observing the
Fig. 3 we can notice that with increasing the packet
size black and white bars are getting more separated.
This behavior is natural as increasing the packet size
causes larger packet error rate.
To summarize the results from our two sets of
experiments: using LOP, given the weight parame-
ters α and β, we experimentally obtain the value of
n = 10,000 blocks as an optimal message size for
both ideal channel and channel with losses. Observ-
ing the simulation results for the relationship between
packet size vs. total overhead it is straightforward
to conclude that the use of smaller packets results in
smaller total overhead and hence - in better perfor-
mance. On the other hand, by decreasing the packet
size we increase the number of packets and as a result
decoding becomes computationally more expensive.
ON THE PRACTICAL PERFORMANCE OF RATELESS CODES
175

Figure 3: Packet size vs. total overhead for four different packet sizes - channel with losses.
7 CONCLUSIONS
In this paper we have proposed a new parameter -
Latency-Overhead Product(LOP) - for finding the op-
timal block size for a message encoded with rateless
codes. We implemented Online codes and showed
how LOP can successfully be used to determine the
optimal block size in terms of best compromise be-
tween latency and data overhead. Experimenting with
the behavior of Online codes in simulated wireless
environment, where the packet error rate is packet-
length dependant, we showed that the use of smaller
block sizes results in a smaller total overhead. Al-
though we experimentally proved the effectiveness of
LOP for evaluating and optimizing the performance
of rateless codes, this parameter can be further inves-
tigated from theoretical point of view. This is a possi-
ble direction for the future work.
REFERENCES
Luby, M. (2002). LT Codes. In In Proceedings of the 43rd
Annual IEEE Symposium on Foundations of Computer
Science (FOCS).
Luby, M. G., Mitzenmacher, M., Shokrollahi, M. A., Spiel-
man, D. A., and Stemann, V. (2001). Efficient erasure
correcting codes. In IEEE Tansactions on Information
Theory vol. 47, No. 2.
MacKay, D. (2005). Fountain codes. In IEEE Proc.-
Commun, Vol. 152, No.6. IEEE.
Maymounkov, P. (2002). Online codes. In NYU Technical
Report TR2002-833.
Maymounkov, P. and Mazieres, D. (2003). Rateless Codes
and Big Downloads. In Lecture Notes in Computer
Science, Springer Berlin/Heidelberg, 0302-9743.
Shokrollahi, A. (2006). Raptor codes. In IEEE Transactions
on Information Theory, vol. 52, pages 2551–2567.
Vukobratovic, D. and Despotovic, M. (2005). On the Packet
Lengths of Rateless Codes. In Computer as a Tool,
EUROCON 2005.
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
176
