
FRAME ERROR RATE EVALUATION OF A C-ARQ PROTOCOL
WITH MAXIMUM-LIKELIHOOD FRAME COMBINING
Julián David Morillo Pozo and Jorge García Vidal
Computer Architecture Department (DAC), Technical University of Catalonia (UPC), Barcelona, Spain
Keywords: Automatic repeat request, Cooperative systems, Diversity methods, Land mobile radio diversity systems,
Protocols.
Abstract: In this paper a Cooperative-ARQ (C-ARQ) with a maximum-likelihood frame combiner (ML-FC) protocol is
studied. C-ARQ is well suited for wireless transmission in either infrastructure or ad-hoc networks, as it
exploits some of the unique characteristics of wireless media, such as the natural broadcast of wireless
transmission and receiver diversity. The frame combiner can help in the case in which any received frame is
correct, exploiting the same characteristics of wireless transmission but at a bit level. The paper studies the
Frame Error Rate for this kind of system, showing that significant improvements can be obtained.
1 INTRODUCTION
This paper deals with a recently proposed variant of
the well known ARQ (Automatic Repeat reQuest)
protocol, called Cooperative-ARQ (C-ARQ) (Miu,
2005), (Monti, 2005), (Morillo, 2005), (Zhao, 2005).
C-ARQ is well suited for wireless transmission in
either infrastructure or ad-hoc networks, as it
exploits the natural broadcast characteristic of
wireless transmission and receiver diversity
(Goldsmith, 2005). As in any ARQ protocol, when a
node receives a frame with erroneous bits, it will ask
for a frame retransmission. In C-ARQ, however, the
node has previously designated a subset of nearby
nodes as cooperator nodes. In case that a cooperator
node has correctly received the frame, it will
perform the retransmission instead of the transmitter
node. In case no cooperator node has the correct
copy of the frame, a retransmission from the
transmitter node will be asked.
In this document, a variant of this basic operation
scheme is studied: when all the cooperator nodes
have erroneous copies of the frame, instead of
asking a retransmission from the transmitting node,
the receiver uses the erroneous frames from them in
an attempt to reconstruct the original one. This
frame reconstruction will be performed by means of
a so-called frame-combiner (FC). The frame-
combining technique studied in this paper is called
maximum-likelihood (ML).
Assume that a node have M-1 cooperators. The
frame-combiner will take bit by bit the M frames
(frames from the receiving node plus frames from
the M-1 cooperator nodes) and will try to produce a
correct copy of the original frame. Although a frame
combiner is a Layer 2 module, -it deals with bits and
not with signals-, it shares some commonalities with
techniques used at physical level, such as the well
known Maximal Ratio Combining (MRC)
technique, that combines different signals received
on different antennas on the same device; see
(Goldsmith, 2005).
The paper presents a numerical evaluation of the
Frame Error Rate (FER) of a C-ARQ protocol with a
maximum-likelihood frame combiner (ML-FC) in
Rayleigh channels. The idea behind the frame
combiner is give to the system a second opportunity
when C-ARQ fails: instead of asking a
retransmission from the source we retransmit from
neighboring nodes of the destination.
Using C-ARQ with a frame combiner can
introduce degradation in throughput, as in some
occasions M-1 cooperator nodes must re-transmit
their incorrect frames to the receiving node. On the
other hand using higher order constellations in the
frame retransmissions from the cooperators could
alleviate this. The study of this, however, will be left
out of the scope of this paper.
The studied scheme does not present major
implementation challenges, as it only involves
changes in the driver software together with the
15
David Morillo Pozo J. and García Vidal J. (2008).
FRAME ERROR RATE EVALUATION OF A C-ARQ PROTOCOL WITH MAXIMUM-LIKELIHOOD FRAME COMBINING.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 15-20
DOI: 10.5220/0002022700150020
Copyright
c
SciTePress

inclusion of new signalling packets (for example for
establishing the relation of cooperation and for
requesting frame copies). The ML-FC operation
requires that each node knows the average SNR
during frame reception. This information is readily
available, with different levels of accuracy, from
many of the wireless NICs used in current networks.
Previous studies on C-ARQ (e.g. (Miu, 2005),
(Monti, 2005), (Zhao, 2005)) report significant
improvements in terms of transmission power,
transmission range or throughput. Reference
(Morillo, 2005) studies a majority voting frame
combiner for AWGN and Rayleigh channels. An
ARQ variant (that the authors call Memory ARQ)
that uses frame combining of erroneous frames was
previously introduced in (Lau, 1986). This work,
however, is not in the framework of cooperative
ARQ, as all the copies come from the original
transmitter. Moreover, (Lau, 1986) analyzes the
performance of such system in an AWGN channel
while our work is focused on Rayleigh fading
channels. The work reported in (Eaves, 1977),
studies the probability of block error (i.e. FER) for
slow Rayleigh fading channels. Although it is not a
work on cooperative techniques nor on ARQ
protocol, it gives to us a good base line scenario to
compare with our proposal.
Next, Section II gives a brief description of the
C-ARQ variant that is studied in this paper. Section
III presents the Maximum-Likelihood (ML) frame
combiner (FC) integrated in the studied C-ARQ
scheme. Section IV presents the evaluation of the
FER for such kind of system.
2 COOPERATIVE ARQ
In this section we give a brief description of the C-
ARQ variant studied in this paper: Let us assume a
wireless ad-hoc network. For a given node x of the
network, we define R
x
as the set of nodes which
receive the signal from x with some minimal quality
parameters. Let y be a node of R
x
, to which node x
wants to send a frame, and let d be the distance
between x and y. From the set R
y
, we form a subset
of cooperating nodes, that we call C
y
, which
includes all nodes from that y receives signals with
an excellent quality (including y itself), and that are
willing to cooperate with y. We assume a perfect
channel between y and nodes in C
y
, due to this
excellent signal quality. Although this is a strong
assumption, it can be justified by the proximity
between y and nodes in C
y
. In the rest of the paper
we assume |C
y
| = M. Usually, we will have that
distance between y and nodes of C
y
will be bounded
to d’, with d’<<d. We can thus approximate the
distance between x and nodes of C
y
to the value d.
We assume that when x transmits a frame
addressed to y, nodes of C
y
observe different values
of SNR, following a Rayleigh distribution:
0
*
1
)(
*
≥=
−
γ
γ
γ
γ
γ
ef
where the average SNR, γ*, is the same for all nodes
and constant with time. We also assume that for
each node, the SNR value is constant during a frame
reception, but it can be different for each frame.
Let x transmit a frame to y, which is received by
nodes of C
y
. We assume that these nodes can
identify that the final destination of the frame is y
even in presence of transmission errors (e.g. using a
strong error correction code for the corresponding
header fields). After receiving the frame, every node
checks for its correctness using for instance a CRC.
For simplicity, it is assumed throughout this paper
that the error detection code used will detect all
errors introduced by the channel. In practice, this is a
reasonable assumption since the probability of an
undetected error can be made very small.
In a C-ARQ system without frame combining,
nodes in C
y
that correctly receive the frame will
keep a copy of it. If node y detects that its reception
is erroneous, it will ask one of these nodes for a
retransmission of a correct copy. Only in the case
that any node in C
y
has correctly received the frame,
y would ask for a retransmission to node x.
In a C-ARQ with FC, in contrast, even if the
frame was received with errors, nodes in C
y
will
keep a temporary copy of it. In case node y finds
that the frame has suffered errors, it will request
their cooperators for a correct copy of the frame. In
case there is no correct frame received by any
cooperator, it will send a signaling packet to its
cooperators requesting a retransmission of their
erroneous frame copies (Figure 1). Cooperators of y
will send, in turns, their copies of the frame,
attaching the measured value of SNR during the
frame reception, γ
i
, until y is able to correctly decode
the frame by performing the frame combining.
Recall that we assume a slow fading channel and,
therefore, that γ
i
is constant during frame reception,
but in general different for each cooperator. At each
reception of the information sent by each cooperator
- and assuming that this received copy of the frame
has not a correct CRC-, terminal y uses a Maximum-
Likelihood (ML) decision rule for constructing a
“hypothetically correct” received frame (Figure 1).
That is, y uses a statistically optimal fusion rule in
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
16

terms of minimum detection error probability. Only
in the case that this reconstructed frame is still
incorrect in the last step (y has received all copies
from all its cooperators), a retransmission is required
from node x (Figure 1) if the maximum number of
such retransmissions has not been exceeded (this
number is normally set to 11 in 802.11 but could be
set below this value for this system with greater
resilience).
Received
frame
End
Correct?
yes
no
Ask for
correct copy
Correct
copy?
yes
no
End
Ask for
incorrect copy
Maximum
Likelihood
Correct?
yes
no
End
# of copies
= M ?
yes
Ask for retransmission
to transmitter
no
Figure 1: Cooperative ARQ scheme with maximum-
likelihood frame combiner.
Note that we do not focus on the order in which
cooperators send their respective frames to y, and we
assume some pre-established order. How this order
is set up is left for future work and is out of the
scope of this document.
This paper studies the impact of C-ARQ and ML
Frame-Combining on the FER.
3 THE ML FRAME COMBINING
TECHNIQUE
The ML decision rule for obtaining a possible
correct copy of the frame is the following: Let
BER
i
(γ
i
)
be the i-th node BER (directly derived from
its SNR, γ
i
). Let S
1
and S
0
be the sets of cooperator
nodes of y that have detected a given bit as 1 or 0
respectively. Assuming that the a-priori probabilities
of “1” or “0” are identical, the ML decision rule for
this bit would be:
Decide “1” if
() ()
()
10
10
1
(1 ( )) ( )
ii ii
iS iS
ii ii
iS iS
BER BER
BER BER
γγ
γ
γ
∈∈
∈∈
−<
−
∏∏
∏∏
(1)
and decide “0” otherwise
Note that when SNR is the same for all cooperating
nodes, then the proposed decision rule is equivalent
to the Majority Voting (MV) scheme proposed in
(Morillo, 2005), due to the fact that all frames have
the same weight. Each cooperator node coherently
detects its own information with a given BER
depending on the modulation scheme used and the
channel model considered. In the case of Rayleigh
channels and for some modulation schemes, this ML
decision rule can be simplified.
4 FER PERFORMANCE
EVALUATION
The exact evaluation of the FER for C-ARQ+FC is
involved, even for simple modulation techniques.
Even the evaluation of FER for C-ARQ leads to
non-closed expressions; see (Eaves, 1977). On the
other hand, FC mechanism only enters into play
when all frames received by a node and its
cooperators are incorrect, meaning that we should
introduce this condition into the probability
expressions.
We take thus the next approach: Firstly, we study
the ML-FC in isolation. Secondly, an analysis of the
performance of C-ARQ without FC is done. It is
easy to show that each of these mechanisms in
isolation would lead always to worse cases than the
C-ARQ+FC mechanism in conjunction. Finally, we
study FER for the combined C-ARQ-FC scheme
using Monte-Carlo simulations. We assume that the
modulation method is BPSK, without loss of
generality.
The expression for the FER for a Rayleigh fading
channel in the case in which no cooperation is
exploited is given by:
()()
[
]
γγ
γ
γ
γ
γ
dBEReFER
L
∫
∞−
−−=
0
*
11
1
)(
*
(2)
where γ* is the average SNR, and L is the frame
length; see (Eaves, 1977). In the case of BPSK
modulation,
(
)
(
)
γγ
2QBER =
. Figure 2 presents
the calculated FER versus frame length L for an
average SNR of 24 dB, which corresponds to a 10
-3
BER.
FRAME ERROR RATE EVALUATION OF A C-ARQ PROTOCOL WITH MAXIMUM-LIKELIHOOD FRAME
COMBINING
17
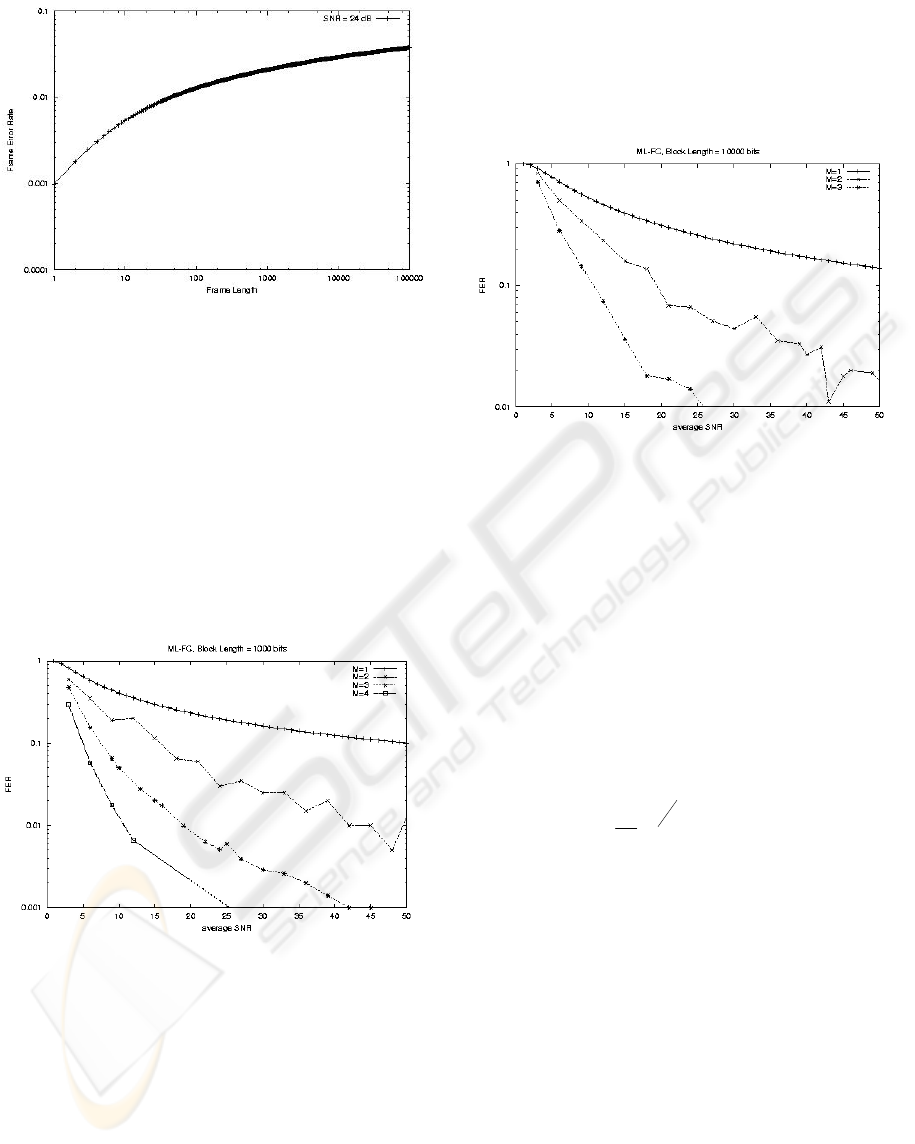
Figure 2: FER vs Frame Length in Rayleigh fading
channels. SNR=24dB. BPSK modulation.
4.1 FER of ML-FC
We focus first on the maximum-likelihood FC
mechanism and study it in isolation. We have
performed a Monte-Carlo simulation calculating the
FER that can be obtained for different values of
average SNR, and for different values of M, the
number of cooperators. Simulations have been done
using OCTAVE for frame lengths (L) equal to 1,000
and 10,000 bits. The results for L=1,000 bits are
presented in Figure 3.
Figure 3: FER of ML-FC vs SNR in Rayleigh fading
channels for different values of M and for L=1000 bits.
BPSK Modulation.
From Figure 3 we can see the great
improvements that can be obtained with the ML-FC
technique studied in this paper. For example, for an
SNR=33 (~15dB) the FER decreases from 0.15 for
the case M=1 -no cooperation- to 0.025 for the case
of just combining two frames, meaning that we have
a reduction of FER of an order of magnitude. In
fact, note that for the case M=2, the ML-FC does not
perform any frame combining and simply chooses
the frame with higher SNR. For M=3 the FER for
the same SNR is about 0.0026. Increasing M, on the
other hand, increases the number of frame
retransmissions.
Figure 4 presents similar results for the case
L=10,000 bits.
Figure 4: FER of ML-FC vs SNR in Rayleigh fading
channels for different values of M and for L=10000 bits.
BPSK Modulation.
4.2 FER of C-ARQ Protocol
Let us focus now on the C-ARQ protocol and study
it in isolation, i.e. without ML-FC, as we have done
for the FC.
An analytical expression can be easily derived
from (2) for the case of C-ARQ. If we have M
cooperating nodes (including the destination node
itself) and considering that the γ
i
are independent
and identically distributed random variables, the
FER of C-ARQ will be:
(3)
This expression represents the FER from the
transmitter point of view, i.e., the probability that a
retransmission from x in the model presented in
Section II would be necessary.
The goodness of the C-ARQ protocol can be
observed in Figure 5, together with the impact of the
number of cooperators in the FER. It can be seen
how FER decays orders of magnitude with just 2 or
3 cooperators.
()()
[
]
∏
∫
=
∞
−
−
−−=
M
i
i
L
iARQC
dBEReFER
i
1
0
*
11
1
*
γγ
γ
γ
γ
M
ARQC
FERFER )]([
γ
=
−
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
18
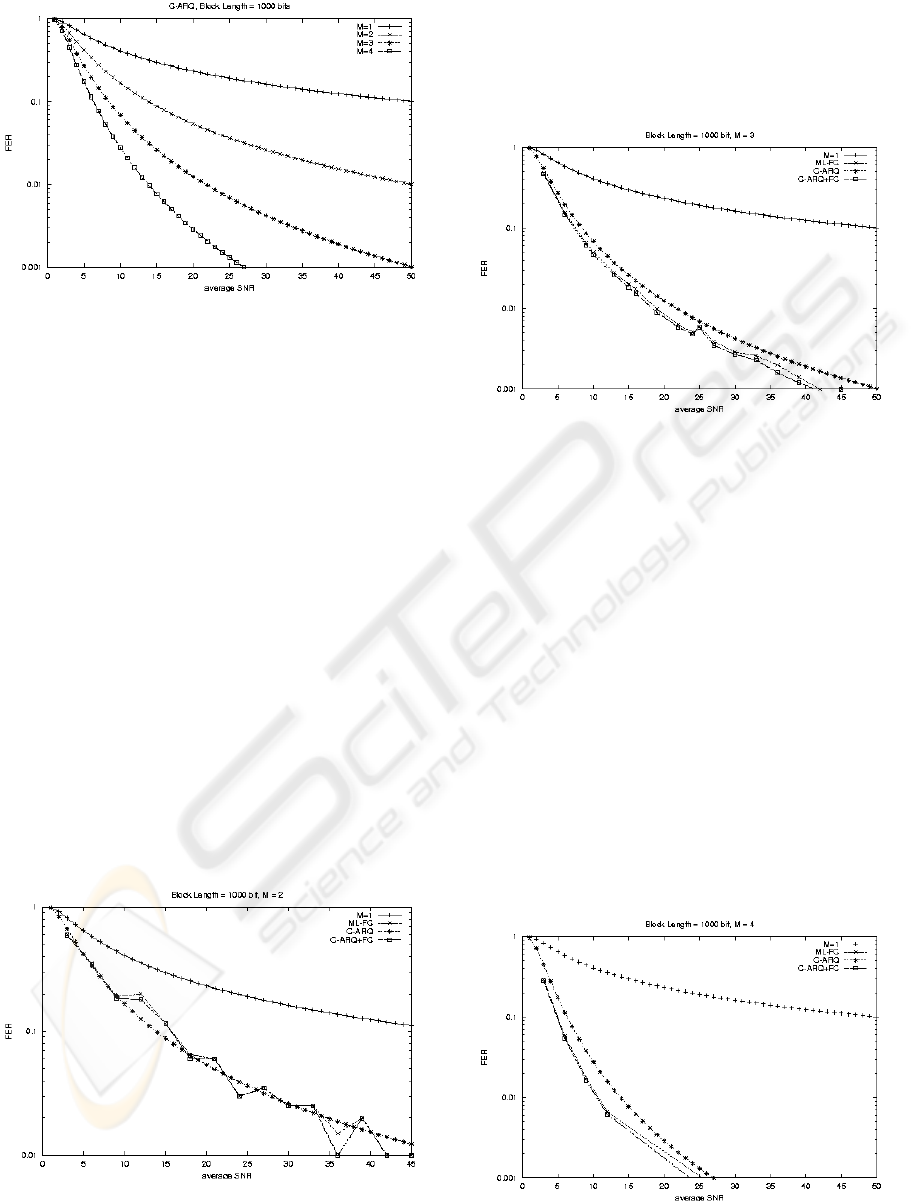
Figure 5: FER of C-ARQ vs SNR in Rayleigh fading
channels for different values of M and for L=1000 bits.
BPSK Modulation.
4.3 FER of Combined C-ARQ +
ML-FC
Once presented the results for each component of
the system in isolation, let us focus on the
performance of such system as a whole.
We have performed simulations for L=1,000 and
10,000 bits, and for different number of cooperators
(M). Figure 6 shows the results for M=2 and M=1. It
is clear that the use of C-ARQ-FC considerably
reduces the overall FER values. Figure 6 is also
interesting for a particularity of the M=2 case:
normally ML-FC in isolation lead to a lower FER
than the C-ARQ in isolation. For M=2, however, this
is not true, as in this case ML-FC in fact does not
perform any frame combining: it will simply choose
the frame with higher SNR (that could be
erroneous). C-ARQ, on the other hand, will choose a
correct frame if it exists. Sometimes it can happen
that the correct frame is the one with lower SNR. In
this case ML-FC will fail while C-ARQ will not.
Figure 6: FER of the whole system vs SNR in Rayleigh
fading channels for M=2 and L=1000. BPSK Modulation.
Figure 7 presents the case M=3 and L=1,000. As
stated previously, ML-FC in isolation performs
better than C-ARQ in isolation, while the
combination of both mechanisms performs only
slightly better than ML-FC.
Figure 7: FER of the whole system vs SNR in Rayleigh
fading channels for M=3 and L=1000. BPSK Modulation.
Figure 8 shows the obtained values for the case
M=4, L=1,000. As expected, similar conclusions can
be drawn, although now the difference between the
C-ARQ in isolation and the combined C-ARQ-FC
scheme is larger.
The question of whether C-ARQ in isolation or
the combined C-ARQ-FC schemes are feasible
alternatives, is very much system dependent, and is
left out of the scope of this paper. The evaluation of
this question depends on factors like the distance
between source and receiver, between receiver and
cooperators, etc. The idea of the FC is to give a
second opportunity in trying to avoid
retransmissions from a source (possibly far away) by
substituting it with transmissions of nearby nodes
that could spend less power. Another open issue
could be the system performance in the case of using
Hybrid-ARQ techniques integrated in the system.
Figure 8: FER of the whole system vs SNR in Rayleigh
fading channels for M=4 and L=1000. BPSK Modulation.
FRAME ERROR RATE EVALUATION OF A C-ARQ PROTOCOL WITH MAXIMUM-LIKELIHOOD FRAME
COMBINING
19

5 CONCLUSIONS
In this paper we study and evaluate the FER for a
cooperative ARQ scheme with a maximum-
likelihood frame combiner integrated in it that
exploits space diversity and cooperation between
neighboring nodes. This paper shows how the
benefits of space diversity and node cooperation
have also a great impact on the FER performance
(maybe more interesting at the Link Layer than the
BER). The hardware complexity of the system is
clearly reduced with respect to MRC or to
cooperative transmission techniques, although new
protocol signaling is needed.
ACKNOWLEDGEMENTS
This work has been supported by Spanish Ministery
of Science and Technology under grant TSI2007-
66869-C02-01 and by the NoE EuroFGI of the VI
FP of EU.
REFERENCES
Goldsmith, A., 2005. Wireless Communications,
Cambridge University Press.
Miu, A., Balakrishnan, H., Koksal, C. E., 2005. Improving
Loss Resilience with Multi-Radio Diversity in
Wireless Networks. In ACM Mobicom 2005.
Monti, P., Tacca, M., Fumagalli, A., 2005. Optimized
Transmission Power Levels in a Cooperative ARQ
Protocol for Microwave Recharged Wireless Sensors.
In IEEE ICC’05.
Morillo-Pozo, J., García-Vidal, J., Pérez-Neira, A., 2005.
Collaborative ARQ in Wireless Energy-Constrained
Networks. In ACM-SIGMOBILE DIAL-M-POMC
International Workshop on Foundation of Mobile
Computing.
Nosratinia, A., Hunter, T.E., Hedayat, A., 2004.
Cooperative communication in wireless networks. In
IEEE Communications Magazine, vol. 42, no. 10, pp.
68-73.
Zhao, B., Valenti, M. C., 2005. Practical Relay Networks:
A Generalization of Hybrid-ARQ. In IEEE JSAC, Vol.
23, No. 1.
Cover, T. M., El Gamal, A. A., 1979. Capacity theorems
for the relay channel. In IEEE Trans. on Information
Theory, pp. 572-584, Sept. 1979.
Laneman, J. N., Tse, D. N. C., Wornell, G. W., 2004.
Cooperative diversity in wireless networks: Efficient
protocols and outage behaviour. In IEEE Trans. on
Information Theory, pp. 3062-3080, Dec. 2004.
Lau, C., Leung, C., 1986. Performance Analysis of a
memory ARQ scheme with soft decision detectors. In
IEEE Trans on Commun., Aug. 1986.
Ishioka, K., Takanashi, H., Tanaka, T., 1995. Improved
Throughput Characteristics by ARQ with weighted
Majority Decision. In Proc. IEEE ICUPC’95, pp. 467-
471.
Eaves, Reuben E., Levesque, Allen H., 1977. Probability
of Block Error for Very Slow Rayleigh Fading in
Gaussian Noise. In IEEE Transactions on
Communications, March 1977, pp. 368-374.
Tacca, M., Monti, P., Fumagalli, A., 2005. Cooperative
and Non-Cooperative ARQ Protocols for Microwave
Recharged Sensor Nodes. In Proc. EWSN’05, pp. 45-
56.
Chen, B., et. al, 2004. Channel aware decision fusion in
wireless sensor networks. In IEEE Transactions on
Signal Processing, Dec. 2004.
Cai, X., et. al, 2003. Performance of CDMA random
access systems with packet combining in fading
channels. In IEEE Trans. on Wireless Commun., May
2003.
Cui, S., et. al, 2004. Energy-efficiency of MIMO and
cooperative MIMO in sensor networks. In IEEE JSAC,
vol. 22, no. 6.
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
20
