
MACRO DIVERSITY COMBINING SCHEMES FOR MULTICAST
TRANSMISSION IN HIGH-SPEED CELLULAR NETWORKS
Neila El Heni and Xavier Lagrange
IT/TELECOM Bretagne, campus de Rennes, BP 35510, France
Keywords:
Chase combining, clustering, multicast transmission, maximum ratio combining, selective combining.
Abstract:
In this paper, we study the transmission of data destined for several users on the radio interface using the
multicast mode, an interesting alternative of the conventional unicast mode. In the multicast mode, a packet is
sent simultaneously to several terminals in the same cell. We consider different techniques of macro diversity,
namely Selective Combining (SC) and Maximal Ratio Combining (MRC).
We develop an analytical model that allows the computation of the mean bitrate for both multicast and unicast
schemes. We use a scheduler that allocates bandwidth to mobiles according to their instantaneous channel
quality. In this context, we propose an efficient user clustering considering their average radio channel quality.
The study shows that macro diversity improves the transmission performance especially for pure multicast.
1 INTRODUCTION
Packet scheduling is the functionality that distributes
radio resources between users. Intensive research has
been conducted on the performance of unicast sched-
ulers in cellular networks (e.g. (Al-Manthari et al.,
2006), (Liu et al., 2003)). During a service ses-
sion, users may experience different channel condi-
tions from a Transmission Time Interval (TTI) to an-
other. The packet scheduler uses the reported channel
qualities and chooses at each TTI the user to serve
with the suitable modulation and coding scheme.
Multicast services have drawn a lot of attention re-
cently. MBMS (Multimedia Broadcast/Multicast Ser-
vice) is currently specified in the 3GPP recommen-
dation. However, the focus is on the access and core
network rather then on the radio interface. The con-
ventional way to manage multicast services on the lat-
ter interface is to duplicate transmissions to the differ-
ent User Equipments (UEs). This may however con-
siderably waste radio resource if several users in the
same cell are registered to the same service as only
one user is served during a TTI. In this paper, such
an approach is called multiple-unicast. An interesting
alternative is to really send a given packet to several
users at the same time. In order to avoid packet losses,
the multicast scheduler must adapt the transmission
bitrate to the mobile that has the lowest Signal to
Noise Ratio (SNR). It is noteworthy that other multi-
cast schedulers can be used such as Multicast Propor-
tional Fairness (MPF) and Inter-group Proportional
Fairness (IPF) (Won et al., 2007). However, packet
losses are frequent with these algorithms and result-
ing retransmissions may decrease the system perfor-
mance.
In a previous paper (El Heni and Lagrange,
2008b), we have studied multicast and multiple-
unicast for several users in the same cell. It was
shown that multicast outperforms multiple-unicast
only when the average SNR is above a given thresh-
old. The main reason is that multicast scheduling has
to consider the worst SNR of the group of users as op-
posed to multiple-unicast scheduler that can choose
at each TTI the user that has the best SNR. Users
with low SNR are generally on the cell border and
may generally receive several base stations (BSs). It
is then interesting to combine transmissions of neigh-
boring BSs to increase the overall received SNR. Note
that the multicast service is not restricted to one cell
but can be delivered over several cells. In this con-
text, the same data transport block (TB) is transmitted
by several BSs. A UE may decode data from these
BSs simultaneously. If at least one copy of the same
TB is correctly received, this block is then considered
successfully transmitted. By extending the TB level
to the signal level, we identify this scheme as Selec-
tive Combining (SC) where a user selects the block
with the maximum SNR. Alternatively, the receiver
may combine replicas of the same flow proportion-
ally to their strength like in Chase Combining (CC)
121
El Heni N. and Lagrange X. (2008).
MACRO DIVERSITY COMBINING SCHEMES FOR MULTICAST TRANSMISSION IN HIGH-SPEED CELLULAR NETWORKS.
In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 121-126
DOI: 10.5220/0002025801210126
Copyright
c
SciTePress
(cha, ). The CC is a scheme of hybrid ARQ protocol
that is used in High Speed Downlink Packet Access
(HSDPA). With CC protocol, if an initial transmis-
sion is received with some errors, the corrupted data
packet is stored at the terminal and retransmissions
of identical coded data packets occur till a successful
reception. Then, the decoder combines these multi-
ple copies weighted by the SNR prior to decoding.
This method provides diversity (time) gain. We pro-
pose to use the same principle but with copies of the
same data block sent by different BSs. Extending the
block level to the physical level amounts to the Max-
imal Ratio Combining (MRC) scheme where redun-
dant signals are also combined proportionally to their
strength. The resulting SNR is then the sum of the
all received SNRs (eur, ). Conventional MRC (at the
signal level) with MBMS has been studied in other
papers, e.g. (Soares and Correia, 2006).
Our objective is to quantify the throughput gain of
applying macro diversity combining schemes to mul-
ticast scheduling. Our multicast scheduler is called
the equal-bitrate scheduler; it allocates bandwidth
to mobiles according to their instantaneous channel
quality. The multicast scheduler is based on a new
clustering strategy. Clustering is the way to define
sub-groups of users, all of them subscribing to the
same service. The new clustering method combines
multicast and unicast schemes according to the user’s
average channel conditions. We have developed it for
a single cell case in (El Heni and Lagrange, 2008a)
but it will be explained here again for the sake of clar-
ity. This paper is organized as follows. In Section 2,
the system model and assumptions are given. In Sec-
tion 3, we define the new clustering strategy. Section
4 explains the proposed equal-bitrate scheduler and
expands the scheduler model with the use of SC and
MRC. Section 5 gives the simulation results. Conclu-
sions are drawn in Section 6.
2 MODEL DESCRIPTION
2.1 General Considerations
In a regular cellular network, each cell has 6 neigh-
boring cells. In a first approach, a cell may be di-
vided in 6 sectors, each of which having one serving
base station and one neighboring one. We restrict our
study to one sector. Let BS1 be the serving base sta-
tion and BS2 the neighboring one. This case is easily
generalized to the whole cell if we consider that fad-
ing values in each sector are independent and then the
system is invariant by rotation. We consider N users
that are randomly distributed in the studied sector rep-
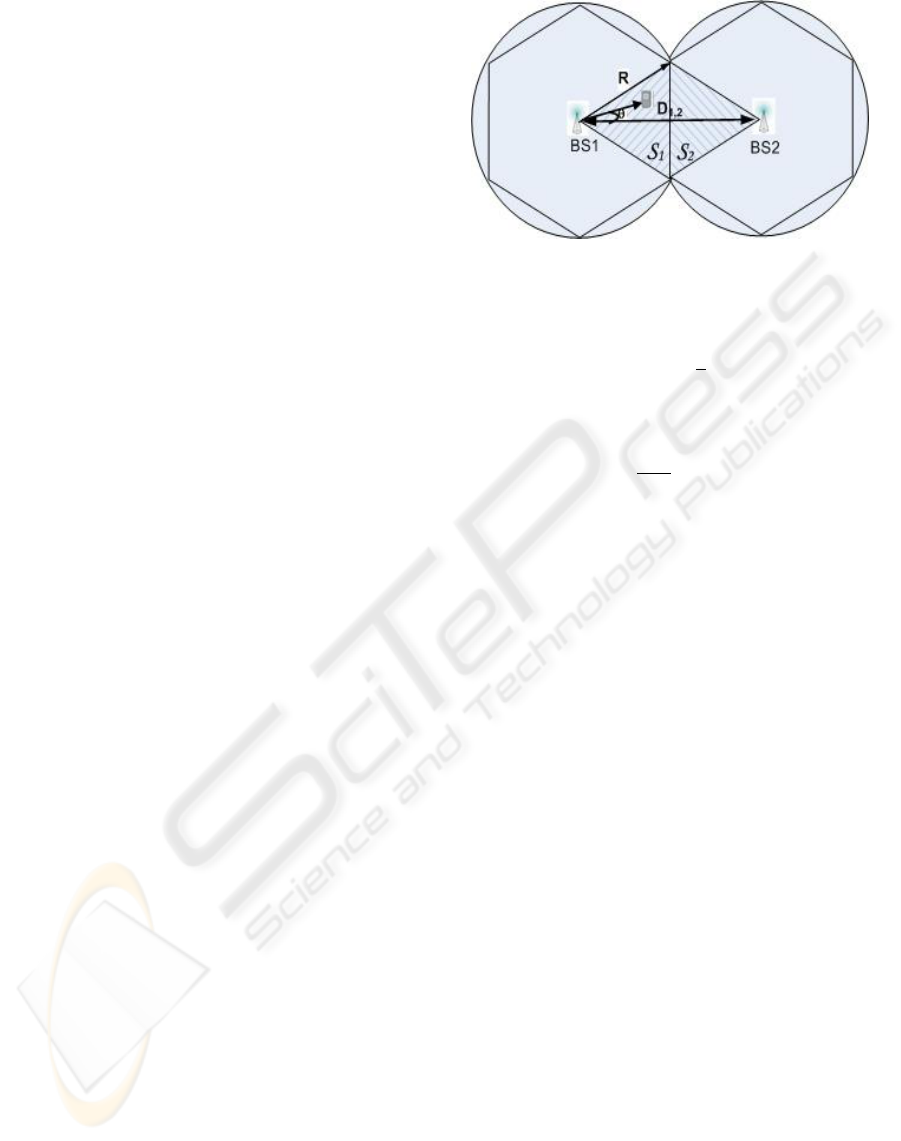
Figure 1: Macro diversity with 2 cells.
resented by the shaded area S
1
in Figure 1. Users are
listening to BS1 and BS2 separated by a distance D
1,2
.
Considering an hexagonal model
D
1,2
=
√
3R (1)
where R is the cell radius. Large-scale mobility as-
pects and time constraints are not considered. Let
γ
s,i, j
be the SNR of signal received by UE i from BS
s within cluster j and γ
s,i, j
its average value. Due to
channel variations, γ
s,i, j
are identical and independent
distribution (iid) variables that change randomly from
one TTI to another. The SNR is assumed to be con-
stant during a TTI. Let γ
i j
be the instantaneous SNR
after macro diversity combining at user i, which is
member of cluster j. We denote G as the number of
clusters and S
j
the size of cluster j. We define β
i j
as
the largest TBS supported by UE i. Let g be the func-
tion that relates β
i, j
to the reported γ
i, j
of the served
user i, hence
β
i j
= g(γ
i, j
). (2)
It is easy to see that g is a strictly increasing function.
Let h be the associated inverse function: γ
i, j
= h(β
i, j
).
Finally, we define γ
j
as the selected SNR for cluster j
and R
j
the mean bitrate of cluster j. Indices i, j and s
may be sometimes omitted for simplicity.
We consider only one multicast group, i.e. all
users in the serving cell listen to the same service.
Scheduling multiple services amounts to managing
priority between these services according to their QoS
requirements. These issues have been extensively de-
veloped in literature (Lundevall et al., 2004), (Kazmi
and Wiberg, 2003) and are out of the scope of our
study.
2.2 Propagation Model
The average SNR received by a UE may be computed
by using a conventional propagation model. The
model is explained via one BS. Let P
i
be the trans-
mit power to user i. The received power, denoted as
P
r
, is then given by
P
r
= P
i
h
i
χ
i
(3)
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
122
where h
i
is the path gain including shadowing, dis-
tance loss and antenna gain between user i and the
BS and χ
i
is the fast fading between user i and the
BS. Variable χ
i
is a random variable which represents
Rayleigh fast fading. It therefore has an exponential
distribution. The signal to interference ratio received
by user i is
γ
i
=
P
i
h
i
χ
i
α(P
max
−P
i
)h
i
χ
i
+ I
ext
(4)
where P
max
is the total transmit power of the cell, α is
the orthogonality factor and I
ext
represents the inter-
cell interference. The average SNR of user i located
at a distance d from the BS is given by
γ
i
(d) =
Z
γ
sup
0
exp
−I
ext
10
A
0
10
d
β
x
P
i
−α(P
max
−P
i
)x
!
dx (5)
where β is the pathloss exponent, A
0
is the distance-
loss at 1 m (with a BS antenna height of 30 m, a UE
antenna height of 1.5 m and a carrier frequency of
1950 MHz) and γ
sup
is defined by
γ
sup
=
P
i
α(P
max
−P
i
)
. (6)
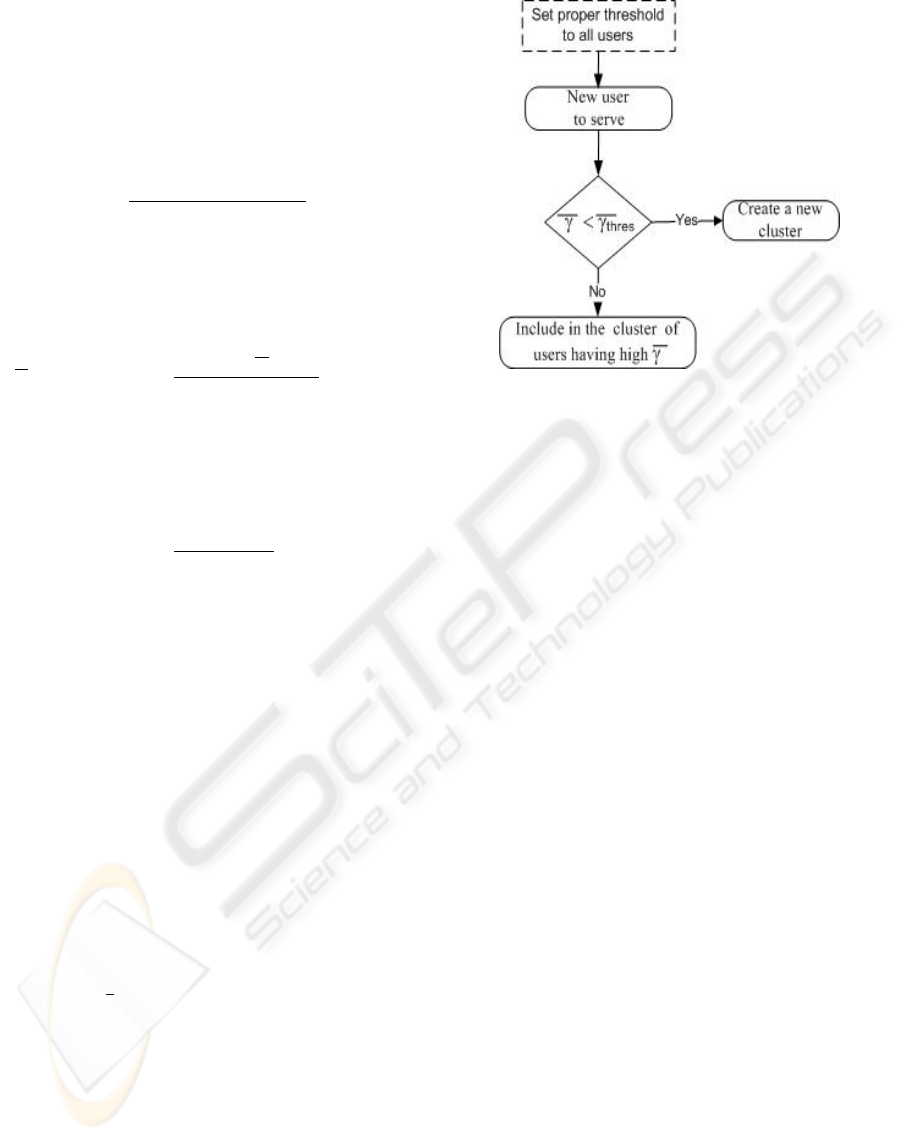
3 PROPOSED CLUSTERING
STRATEGY
Clustering is the way to define sub-groups of users,
all of them subscribing to the same service. We pro-
pose a new clustering method called mixed cluster-
ing; it combines multicast and unicast schemes ac-
cording to the user’s average channel conditions. We
have seen in (El Heni and Lagrange, 2008b) that mul-
ticast outperforms multiple-unicast only for high av-
erage SNRs (above around 3.7 dB). Our clustering
scheme is then deduced as illustrated in Figure 2:
• An average SNR threshold is fixed so that the sys-
tem can differentiate users. The average SNR is
declared as “low” if it is below a threshold value
denoted as γ
thres
. Let N
low
be the number of users
having a low average SNR.
• Users with low average SNRs have to be sepa-
rated from each other. In fact, if the cluster size
increases for low SNR values, the instantaneous
bitrate capacity within the cluster becomes lower
as the multicast strategy is conservative. Our so-
lution is to serve these users according to a unicast
scheme.
• Users with high average SNRs should follow a
multicast scheme. They are grouped in the same
Figure 2: Proposed clustering strategy.
cluster which contains N −N
low
users. Conse-
quently, the resulting number of clusters G is
equal to N
low
+ 1. Of course, if all users have low
average channel quality, G is equal to N
low
.
4 MULTICAST SCHEDULING
WITH SC AND MRC
4.1 Proposed Multicast Scheduler
In this study, we propose a scheduling scheme called
the equal-bitrate scheduler. It aims at increasing fair-
ness among multicast clusters while offering good
system throughput. Equal-bitrate scheduling is per-
formed in two steps. First, the scheduler determines
the convenient transmission bitrate for each cluster.
The intra-cluster bitrate allocation strategy is conser-
vative. We have then
γ
j
= min
i=1..S
j
γ
i, j
(t). (7)
We denote P
X
(x) as the cumulative distribution func-
tion (CDF) of a random variable X. Similarly, p
X
(x)
denotes the probability distribution function (PDF) of
X. Hence, the CDF of γ
j
is equal to
P
γ
j
(x) = 1 −
S
j
∏
i=1
1 −P
γ
i, j
(x)
. (8)
Once the bitrate of each cluster is determined, the
scheduler chooses the cluster to serve. In order to
maximize the global throughput, a natural solution is
to serve the cluster having the highest bitrate capac-
ity. However, the scheduling must guarantee fairness
between clusters. This may be achieved by realizing
MACRO DIVERSITY COMBINING SCHEMES FOR MULTICAST TRANSMISSION IN HIGH-SPEED CELLULAR
NETWORKS
123

the same average bitrate for all the clusters. For this
purpose, we define fairness factors M
j=1..G
such that
the scheduler serves the cluster having a higher bi-
trate capacity with a lower probability, i.e. time is not
uniformly shared between clusters. At instant t, clus-
ter j is served if the product of its instantaneous SNR
and its corresponding fairness factor M
j
is the highest
among all the clusters; hence, if and only if
γ
j
M
j
= max
l=1..G
(γ
l
M
l
). (9)
It can be established that the mean bitrate used to
serve cluster j is
R
j
=
1
D
T TI
Z
∞
0
"
p
γ
j
(x)g(x)
G
∏
l=1,l6= j
P
γ
l
(
xM
j
M
l
)
#
dx
(10)
where D
T T I
is the TTI duration. Equation (10) gives
a general formula for the average bitrate per cluster
j once the clusters are made. Note that this formula
depends on {M
j
}. The value of {M
j
}
j=1..G
is fixed
so that ∀j = 2..G, R
1
= R
j
; with M
1
=1. The value of
G is determined by the clustering scheme detailed in
Section 3.
In the context of multiple-unicast, N single-user
clusters are considered. The individual mean bitrate
is derived from (10) for G = N (S
j
= 1 ∀j = 1..G).
R
j
=
1
D
T T I
Z
∞
0
"
p
γ
j
(x)g(x)
N
∏
l=1,l6= j
P
γ
l
(
xM
j
M
l
)
#
dx.
(11)
In the framework of pure multicast, the average bitrate
denoted as R
mcast
is derived from (10) for G=1. After
a few computation, we obtain
R
mcast
=
1
D
T T I
Z
∞
0
N
∏
i=1
[1 −P
γ
i
(h(x))]
!
dx. (12)
4.2 SC with Multicast Scheduling
According to selective combining, a user selects the
data bloc yielding the highest SNR. We have then
γ
i, j
= max
s=1..S
(γ
s,i, j
) (13)
where S is the number of BSs received by a user (in
the framework of this study S = 2). The CDF of γ
i, j
is given by
P
γ
i, j
(x) =
S
∏
s=1
P
γ
s,i, j
(x). (14)
Combining equations (8), (10) and (14), we have the
average bitrate per cluster with SC and denoted as
R
j,SC
R
j,SC
=
1
D
T T I
Z
∞
0
[p
γ
j
(x)g(x)
G
∏
l=1,l6= j
(15)
[1 −
S
l
∏
i=1
(1 −
S
∏
s=1
P
γ
s,i,l
(
xM
j
M
l
))]]dx.
4.3 MRC with Multicast Scheduling
The case of MRC is more complex than SC. In fact, as
terminals combine the different transmissions propor-
tionally to their strength, the resulting SNR for user i
is given by (eur, )
γ
i, j
=
∑
s=1..S
γ
s,i, j
. (16)
The CDF of the SNR for user i is given by
P
γ
i, j
(x) = Pr(
∑
s=1..S
γ
s,i, j
≤ x ) (17)
When S=2, we define δ
i, j
as follows
δ
i, j
= γ
2,i, j
−γ
1,i, j
. (18)
The CDF of γ
i, j
is given by
P
γ
i, j
(x) =
−γ
2,i, j
exp(
−x
γ
2,i, j
) + γ
1,i, j
exp(
−x
γ
1,i, j
) + δ
i, j
δ
i, j
.
(19)
Then, the average bitrate per cluster for MRC and de-
noted as R
j,MRC
can be easily deduced for S = 2 if
equations (8), (10) and (19) are combined.
R
j,MRC
=
1
D
T T I
Z
∞
0
p
γ
j
(x)g(x)
G
∏
l=1,l6= j
[1 −
S
l
∏
i=1
(20)
(1 −
−γ
2,i,l
exp(
−xM
j
M
l
γ
2,i,l
) + γ
1,i,l
exp(
−xM
j
M
l
γ
1,i,l
) + δ
i,l
δ
i,l
)]dx.
4.4 Application to a Generic System
In (Knopp and Humblet, 1995), it was proposed a ref-
erence radio channel model based on an exponential
distribution for γ. Hence
P
γ
(x) = 1 −exp(−x/γ) if x > 0. (21)
Supposing that each signal received by a UE follows
an exponential distribution for the SNR, equation (15)
is reformulated as follows
R
j,SC
=
1
D
T T I
Z
∞
0
[p
γ
j
(x)g(x)
G
∏
l=1,l6= j
(22)
[1 −
S
l
∏
i=1
(1 −
S
∏
s=1
[1 −exp(−
xM
j
M
l
γ
s,i, j
)])]]dx.
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
124

Table 1: Simulation parameters.
Frame period 2 (ms)
BS Transmission power 38 (dBm)
Intra-cell interference 30 (dBm)
Inter-cell interference -100 (dBm)
β 3.52
A
0
31.8 (dB)
W 5 (MHz)
In the case of pure multicast, equation (12) is rewrit-
ten for SC as follows
R
mcast,SC
=
1
D
T T I
Z
∞
0
N
∏
i=1
(1 −
S
∏
s=1
[1 −exp
−h(x)
γ
s,i
])dx.
(23)
as for multiple-unicast with SC, equation (11) is
rewritten as follows
R
j,SC
=
1
D
T T I
Z
∞
0
p
γ
j
(x)g(x)
N
∏
l=1,l6= j
S
∏
s=1
[1 − (24)
exp(
−xM
j
M
l
γ
s,l
)]dx
Function g is given by Shannon formula (Shannon,
1948): g(γ
i
) = W D
T T I
log
2
(1 + γ
i
) where W is the
available bandwidth. Function h is then h(x) =
2
x/W D
T T I
−1.
In the context of MRC with pure multicast, equation
(12) is rewritten for S = 2 as follows
R
mcast,MRC
=
1
D
T T I
Z
∞
0
N
∏
i=1
(1 − (25)
−γ
2,i, j
exp(
−h(x)
γ
2,i, j
) + γ
1,i, j
exp(
−h(x)
γ
1,i, j
) + δ
i, j
δ
i, j
)dx.
As for MRC with multiple-unicast, we combine equa-
tions (11) and (19) as follow
R
j,MRC
=
1
D
T T I
Z
∞
0
[p
γ
j
(x)g(x)
N
∏
l=1,l6= j
(26)
−γ
2,l
exp(
−xM
j
γ
2,l
M
l
) + γ
1,l
exp(
−xM
j
γ
1,l
M
l
) + δ
i, j
δ
i, j
]dx.
5 EVALUATION RESULTS
In this section , we evaluate the gain of macro di-
versity techniques for different clustering schemes,
namely mutliple-unicast, pure multicast and mixed
clustering. Simulation parameters are listed in Table
1. We perform 120 iterations with different user dis-
tributions. Only one multicast service is considered.
We evaluate results for 5 and 10 randomly distributed
users located in cell 1 and listening to BS1 and BS2
(S=2). As we restrict ourselves to one service and one
cell, these numbers remain reasonable. In the case of
mixed multicasting, we fix γ
thres
to 3.7 dB as found
in (El Heni and Lagrange, 2008b). Results of the av-
erage bitrate performance for SC with the 95% con-
fidence intervals are depicted in Table 2. We see that
macro diversity using SC improves the system perfor-
mance. Gains for pure multicasting are of 20% and
18% for 5 and 10 UEs, respectively. In fact, the per-
formance of this scheme depends only on the lowest
SNR value; as the SC technique increases the chan-
nel quality particularily for users at the cell border
(i.e. having the lowest SNR), it has a direct impact
on the pure multicast scheduler. In the case of mixed
clustering, gains are of 8.5% and 6.5% for 5 and 10
UEs, respectively. With multiple-unicast, the gain is
of 7% and 5% for 5 and 10 UEs, respectively. Gains
of macro diversity with multiple-unicast and mixed
clustering are lower than those obtained for pure mul-
ticast. In fact, users with the lowest SNRs are served
in a unicast scheme and increasing their average chan-
nel quality allows a better bitrate capacity for these
users, the impact on the global system is less visible.
SC allows users with higher SNRs to be served more
frequently as the deviation between the lowest and the
highest average SNR is cut off. Results for Maximum
Ratio Combining are depicted in Table 3. Achieved
gains are higher than those achieved with MRC. Gains
for pure multicasting are of 31% and 28% for 5 and
10 UEs, respectively. In the case of multiple-unicast,
gains are of 12% and 9% for 5 and 10 UEs, respec-
tively. As for mixed clustering, gains are of 15.5%
and 14% for 5 and 10 UEs, respectively. It is note-
worthy that when N increases, user location tend to
concentrate in the middle of the cell where the signal
level is quite high. This is the reason for the decrease
of macro diversity gain.
6 CONCLUSIONS
In this study, we consider macro diversity in the
framework of multicast scheduling over high-speed
networks. We have developed an analytical model
for the mean bitrate calculations in order to evaluate
the resulting scheduling performance. To ensure an
optimal usage of our scheduler, we have used a clus-
tering strategy that classifies terminals according to
their average channel quality. We have shown that
macro diversity using selective combining and max-
imum ratio combining improves the system perfor-
mance. The study shows that the macro diversity gain
MACRO DIVERSITY COMBINING SCHEMES FOR MULTICAST TRANSMISSION IN HIGH-SPEED CELLULAR
NETWORKS
125
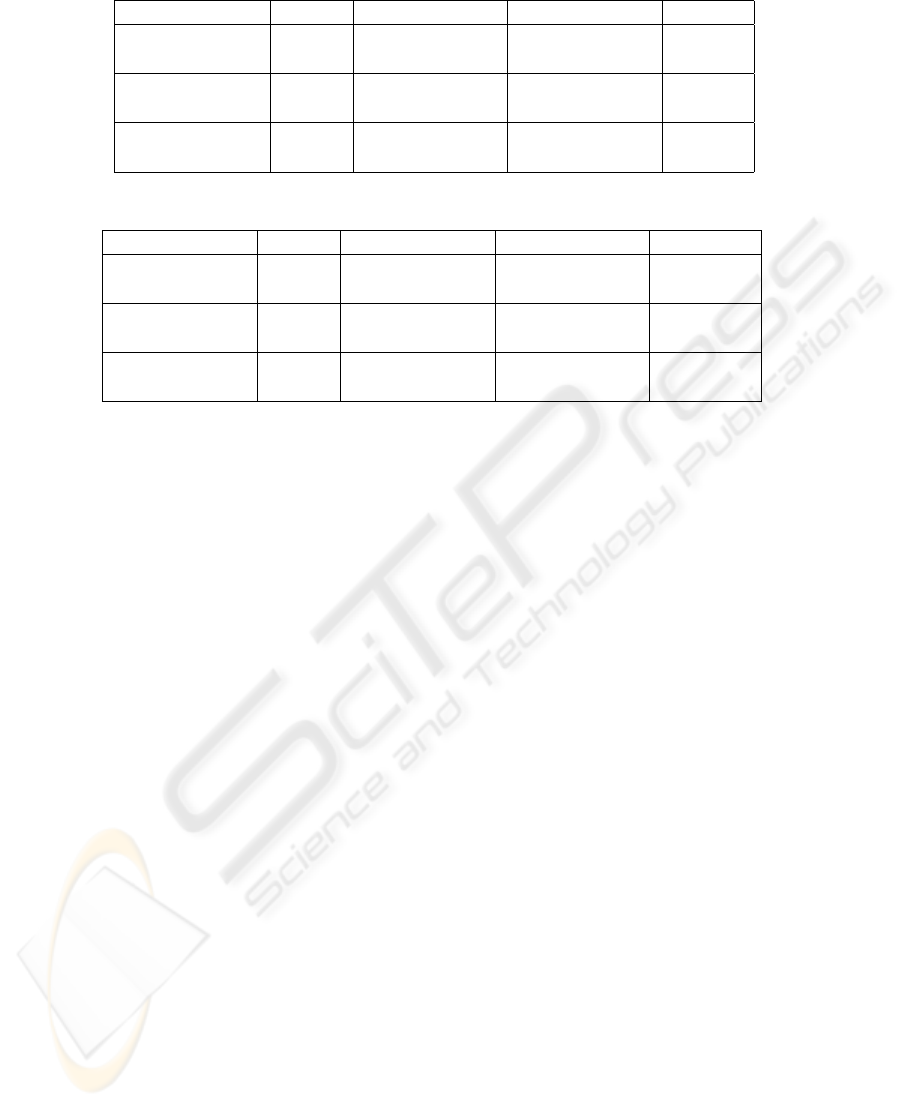
Table 2: Throughput (bps) with confidence intervals for different clustering strategies with/without SC.
Strategy N without SC with SC SC Gain
Pure multicast
5 UEs 4.28 10
6
±3.8% 5.14 10
6
±4% 20%
10 UEs 3.33 10
6
±4% 3.92 10
6
±5% 18%
Multiple-unicast
5 UEs 3.47 10
6
±3% 3.71 10
6
±2.3% 7%
10 UEs 2.45 10
6
±3.5% 2.57 10
6
±2% 5%
Mixed strategy
5 UEs 5.07 10
6
±2.9% 5.49 10
6
±2.8% 8.5%
10 UEs 4.19 10
6
±3.4% 4.45 10
6
±2.9% 6.5%
Table 3: Throughput (bps) with confidence intervals for different clustering strategies with/without MRC.
Strategy N without MRC with MRC MRC Gain
Pure multicast
5 UEs 4.28 10
6
±3.8% 5.60 10
6
±4% 31%
10 UEs 3.33 10
6
±4% 4.31 10
6
±2.8% 28%
Multiple-unicast
5 UEs 3.47 10
6
±3% 3.82 10
6
±3.4% 12%
10 UEs 2.45 10
6
±3.5% 2.67 10
6
±3.3% 9%
Mixed strategy
5 UEs 5.07 10
6
±2.9% 5.85 10
6
±2.6% 15.5%
10 UEs 4.19 10
6
±3.4% 4.78 10
6
±3% 14%
is the highest for the pure multicast scheme. Consid-
ering multiple-unicast and mixed clustering, we ob-
tain equivalent results.
To exploit efficiently the advantages of macro di-
versity, some optimizations have to be considered in
relation with the feedback procedure and retransmis-
sion management. This could be considered in a fu-
ture work.
REFERENCES
Eurane user guide (release 1.6) http://www.ti-
wmc.nl/eurane/. september 2005.
Physical layer aspects of UTRA high speed downlink
packet access. 3GPP TS 25.848 v4.0.0. april 2001.
Al-Manthari, B., Nasser, N., and Hassanein, H. (2006). Fair
channel quality-based scheduling scheme for HSDPA
system. In Computer Systems and Applications. IEEE
International Conference on.
El Heni, N. and Lagrange, X. (2008a). Multicast trans-
mission and clustering schemes in high-speed cellular
networks. In submission to annals of telecommunica-
tions.
El Heni, N. and Lagrange, X. (2008b). Multicast vs
multiple-unicast scheduling in high-speed cellular
networks. In IEEE 62nd Vehicular Technology Con-
ference (VTC).
Kazmi, M. and Wiberg, N. (7-10 Sept. 2003). Scheduling
algorithms for HS-DSCH in a WCDMA mixed traffic
scenario. Personal, Indoor and Mobile Radio Com-
munications, 2003. PIMRC 2003. 14th IEEE Proceed-
ings on, 2:1485–1489.
Knopp, R. and Humblet, P. A. (1995). Information capac-
ity and power control in single-cell multiuser commu-
nications. IEEE International Conf. on Communica-
tions, Seattle, pages 331–335.
Liu, X., Chong, E. K. P., and Shroff, N. B. (2003). A
framework for opportunistic scheduling in wireless
networks. Computer Networks, pages 451–474.
Lundevall, M., Olin, B., Olsson, J., Wiberg, N., Wanst-
edt, S., Eriksson, J., and Eng, F. (2004). Stream-
ing applications over HSDPA in mixed service scenar-
ios. In IEEE 60th Vehicular Technology Conference.
VTC2004-Fall., pages 841 – 845.
Shannon, C. (1948). A mathematical theory of communi-
cation. Bell System Technical Journal, 27:379–423,
623–656.
Soares, A. and Correia, A. (2006). Macro diversity com-
bining techniques for multimedia broadcast/multicast
services in UMTS networks. Wireless Communi-
cations and Networking Conference (WCNC) 2006.
IEEE, 2:685–690.
Won, H., Cai, H., Eun, D. Y., Guo, K., Netravali, A., Rhee,
I., and Sabnani, K. (2007). Multicast scheduling in
cellular data networks. In INFOCOM, 26th IEEE
International Conference on Computer Communica-
tions, pages 1172–1180.
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
126
