MIMO-OFDM CHANNEL ESTIMATION

A Pilot Sequence Design for Time-domain Processing

Carlos Ribeiro

Instituto Politécnico de Leiria, Morro do Lena – Alto Vieiro, Leiria, Portugal

Atílio Gameiro

Instituto de Telecomunicações, Universidade de Aveiro, Aveiro, Portugal

Keywords: OFDM, MIMO, pilot-aided channel estimation, pilot sequence design, time-domain processing.

Abstract: A pilot sequence design for MIMO-OFDM systems is investigated where all transmit antennas share the

same sub-carriers to convey pilot symbols. The pilot sequences are endowed with phase-shifting properties,

granting the receiver the possibility of extracting the impulse responses for all channels directly from the

antennas’ time-domain received signals, without co-channel interference. A linear processing of the time-

domain samples is all that is needed to get the channel impulse responses, resulting in an algorithm with

very low computational load. The feasibility of the investigated method is substantiated by system

simulation using indoor and outdoor broadband wireless channel models.

1 INTRODUCTION

Future mobile broadband applications will require

reliable high data-rate wireless communication

systems. In recent years, multiple-input multiple-

output orthogonal frequency division multiplexing

(MIMO-OFDM) transmission systems (Nee, 2000),

(Stuber, 2004), (Sampath, 2005), (Paulraj, 2004),

emerged as the scheme with the potential to fulfill

these conditions, with bandwidth efficiency and

robustness to frequency selective channels, common

in mobile personal communication systems.

The accurate extraction of the channel state

information is crucial to realize the full potential of

the MIMO-OFDM system. The performance of the

channel estimator is vital for diversity combining,

coherent detection and decoding, and resource

allocation operations. The co-channel interference

inherent to the system, where the received signal is

the superposition of the signals transmitted

simultaneous from the different antennas, puts an

additional challenge on the design of the channel

estimation algorithm.

A decision-directed channel estimation scheme

that attempted to minimize the co-channel

interference was published in (Li, 1999). The

proposed algorithm exhibits a high computational

load. A simplified and enhanced algorithm,

introducing a data-aided scheme for the data

transmission mode, is presented in (Li, 2002). The

topic attracted a significant attention and has been

the focus of investigation in multiple publications

(Shin, 2004), (Zhang, 2005), (Zamiri-Jafarian, 2007)

and references therein.

The design of training symbols and pilot

sequences with the ability to decouple the co-

channel interference and minimize the channel

estimation mean square error (MSE) for MIMO-

OFDM was addressed in several publications (Li,

2002), (Barhumi, 2003) and (Minn, 2004).

Most publications on the topic of training-signal

or pilot-aided channel estimation use the frequency-

domain (FD) least squares (LS) estimates as the

starting point for the analysis of the estimation

algorithm or the design of the training sequence. It

was established in (Ribeiro, 2007) that in single-

input single-output (SISO) OFDM a time-domain

(TD) equivalent LS estimate could be obtained using

a simple linear operation on the received signal, if

the used pilot sequence fulfills certain conditions

(training sequences were treated as particular pilot

sequences with no data symbols in-between

consecutive pilot sub-carriers).

163

Ribeiro C. and Gameiro A. (2008).

MIMO-OFDM CHANNEL ESTIMATION - A Pilot Sequence Design for Time-domain Processing.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 163-170

DOI: 10.5220/0002026101630170

 SciTePress

In this paper we develop a MIMO-OFDM pilot

sequence design and associated channel estimation

method that succeeds in extracting each channel

impulse response (CIR) estimate with minimal

computational load. The investigated scheme can be

used in either spatial multiplexing or space-time

coded systems, with all transmit antennas sharing

the same sub-carriers to convey its individual pilot

sequences, thus minimizing the system’s pilot

overhead. Using different phase-shifting pilot

sequences for each transmit antenna, together with

the result in (Ribeiro, 2007), the method succeeds in

separating the overlapping FD received pilots

sequences by using a TD algorithm that successfully

estimates the different CIRs and eliminates the co-

channel interference, under given conditions. The

STC algorithm (Li, 1999) or the TD LMMSE

criterion (Edfors, 1996) can be incorporated to

improve the estimate at little or no added

computational cost.

The paper is organized as follows. Next Section

gives a brief introduction to the wireless multipath

channel and the MIMO-OFDM baseband model. In

Section 3 the investigated pilot sequence design is

developed. The feasibility of the new method is

substantiated by simulation results presented in

Section 4. Finally, conclusions are drawn in Section

2 MIMO-OFDM IN MOBILE

WIRELESS CHANNELS

Before introducing the investigated method, we will

briefly overview the mobile wireless multipath

channel and the considered MIMO-OFDM baseband

model.

Throughout the text, the notation

()

is used for

TD vectors and elements and its absence denotes FD

vectors and elements. The index n denotes TD

elements and k FD elements. Unless stated

otherwise, the vectors involved in the

transmission/reception process are column vectors

with

N complex elements. The superscripts

()

and

()

denote transpose and Hermitian transpose,

respectively.

2.1 The Wireless Multipath Channel

Let’s consider that the system transmits over

multipath Rayleigh fading wireless channels,

modeled by the discrete-time CIR,

Figure 1: MIMO-OFDM baseband system model.

[]

hn n

δτ

−

=−

⎡⎤

⎣⎦

∑



, (1)

where L is the number of channel paths,

and

are the complex value and delay of path l,

respectively. The paths are assumed to be

statistically independent, with normalized average

power,

−

∑

, where

is the average power

of path l. The channel is time-variant due to the

motion of the mobile terminal (MT), but we will

assume that the CIR is constant during one OFDM

symbol. The time dependence of the CIR is not

present in the notation for simplicity. Assuming that

the insertion of a long enough cyclic prefix (CP) in

the transmitter assures that the orthogonality of the

sub-carriers is maintained after transmission, the

channel frequency response (CFR) can be expressed

as,

[]

exp

hk j kl

−

⎡⎤

=−

⎢⎥

⎣⎦

∑

, (2)

where

N is the total number of sub-carriers of the

OFDM system.

2.2 MIMO-OFDM Baseband Model

Let’s consider the MIMO-OFDM baseband system

with

n transmit antennas and

n receive antennas

depicted in Figure 1. The system uses

N M-ary

PSK or QAM modulated sub-carriers. At time n, the

binary data vector b is coded into

n modulating

vectors

{

}

:1,,

n=d …

. The transmit antennas

simultaneously send

n OFDM signals modulated

d .

To assist in the channel estimation process, pilot

symbols are multiplexed together with data symbols.

OFDM

Mod

OFDM

Mod

Frame

OFDM

DeMod

OFDM

DeMod

De-

Frame

De-

Frame



Decision

Channel

Estimation

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

164

Each antenna path uses a different FD pilot vector

p . Vectors

d and

p contain non-zero values at

disjoint positions (sub-carriers). The resulting FD

signal transmitted by antenna s is

s=d+p.

The OFDM modulator present on each antenna

path performs an

N -points inverse discrete Fourier

transform (IDFT) operation to transform the vector

s to TD. An L samples long guard interval, in the

form of CP, is prefixed to the resulting vector.

Antenna s TD transmitted vector



is,

()

CP s CP s s

s=A Fs=A d+p





, (3)

where

(

)

1, 1

,0,0

jkn

−

F  is the

discrete Fourier transform (DFT) matrix and

CP N L N×

⎡⎤

⎣⎦

AII

is the matrix that adds the CP,

with

I denoting the

identity matrix and

NL×

I denoting the last L columns of

I . The TD

vectors



and



collect, respectively, the

components of data symbols and pilot symbols

present in



The transmission over uncorrelated wireless

channels results in a received signal vector



receive antenna r consisting of

n superimposed

transmitted signal samples,

'' '

rrs rss

−−

=+= +

∑∑

yywHsw



 

, (4)

where the vector



is made-up of independent and

identically distributed (iid) zero mean additive white

Gaussian noise (AWGN) samples with variance

. The vector

rs rs s



represents the

contribution from transmit antenna s to the received

signal;



is the

()()

NLNL+× +

lower

triangular Toeplitz channel convolution matrix with

first column

rs N×

⎡⎤

⎣⎦



, where

,rs



is the column

L-vector with the discrete-time CIR from transmit

antenna s to receive antenna r and

N×

is a null

N -vector.

With the assumption that the signals in the

receive antennas are mutually uncorrelated, the

channel estimation at the receiver will be

independent for all channels and, in the following,

the receive antenna index will be dropped for

notation simplicity.

The OFDM demodulator in each receiving

antenna path starts by removing the CP from each

symbol. The resulting vector for symbols with pilots

and data is,

()

CP CP s CP s s CP

ss s s

−

−−

== +

=+=+

∑

∑∑

rRy RHA d+p Rw

Hd+p w r w



, (5)

where

CP N L N×

⎡

⎤

⎣

⎦

R0I

is the matrix that

removes the CP,

wRw



is the TD noise vector,

(

)

ss s

=rHd+p



represents the contribution from

transmit antenna s to the received vector and

CP s CP

=HRHA



is the

NN× circulant matrix

for channel s, with circulant vector

()

×−

⎡⎤

⎣⎦



The symbols are transformed back to FD with a

DFT operation. The resulting FD column

N -vector

can be expressed as,

()

ss s

−

∑

rFr Hd+p w



, (6)

where

H is the

diagonal matrix whose

diagonal elements are defined by (2) and w is the FD

noise vector.

The deframing block in each receive antenna

path separates the signals in the sub-carriers

conveying pilots and data symbols. The signals in

the data sub-carriers are fed to the decision block.

3 A PILOT SEQUENCE DESIGN

FOR TD PROCESSING

The channel estimation algorithm must estimate the

nn channels from the receive antennas’ signals.

The proposed method estimates the channels from

the symbols carrying pilots and data (the training

sequence is a particular case and the results can be

easily extended to it). All the processing required to

estimate the CIR is performed immediately on the

TD received vector



, eliminating the need to go

from TD to FD and back to TD to finally obtain the

CIR estimate (Li, 1999), (Li, 2002). The present

MIMO-OFDM CHANNEL ESTIMATION - A Pilot Sequence Design for Time-domain Processing

165

algorithm has a very low computational load and no

performance trade-offs. Under given conditions, the

co-channel interference is entirely eliminated. Data-

aided channel estimation algorithms (Li, 2002) can

be incorporated to further improve the algorithm’s

performance.

Consider the set of sub-carriers

℘

dedicated to

convey pilot symbols,

{}

0, , 2 , ,

ff Cf

NN NN℘= − , (7)

where the pilot distance

N can range from 1

(particular case where all sub-carriers in the OFDM

symbol are dedicated to transmit pilots – training

symbol) to

N , fulfilling the condition

=∈

. The set ℘ is common to all transmit

antennas (pilot sub-carriers overlap in receive

antennas).

The system uses distinct phase-shifted pilot

sequences in each transmit antenna. The k-th

element of the column

N -vector

p is defined by,

[]

exp

pk k mN

−

⎡⎤

−

⎡⎤

=−

⎢⎥

⎣⎦

∑

, (8)

giving rise to the corresponding TD vector



whose n-th element is,

[]

fS S

pn k mN e e

sNt

nNmN

Nn n

−−

−

⎡⎤

=−

⎣⎦

⎡⎤

=−−∈

⎢⎥

⎣⎦

∑∑

∑





, (9)

or equivalently,

[] []

[]

ntt

pn nmN

pn n N mN

pn n NmN

−

⎧

=−

⎪

⎡⎤

⎪

=−−

⎪

⎢⎥

⎨

⎣⎦

⎪

⎡

⎤

−

⎪

=−−

⎢

⎥

⎪

⎣

⎦

⎩

∑







. (10)

Equation (10) shows that the transmit antennas’

pilot sequences do not overlap in TD, allowing the

separation of each transmit antenna’s CIR, as it will

be demonstrated.

The n-th element of



can be expressed by,

[] []

dn dke

−

∉℘

∑



, (11)

where

[

]

dk is the k-th element of

d (complex

data symbol conveyed by the k-th sub-carrier).

Replacing equation (9) in equation (5), the n-th

element of



is,

[] [] [] [] [ ]

[]

[] [ ]

[]

000

00 0

sss

ssl

stt

sl m

ntt

rn rn wn hldnl

hn N mN wn

hldn l hn mN

hn N mN

hn NmN

−−

−

===

−

== =

−

=+= −

⎡⎤

+−−+

⎢⎥

⎣⎦

=−+−

⎡⎤

+−−+

⎢⎥

⎣⎦

⎡⎤

−

+−−

⎢⎥

⎣⎦

∑∑∑

∑∑

∑∑ ∑

∑







 







[]

−

∑



. (12)

Equation (12) puts in evidence that antenna r

received signal is the sum of three distinct

components: the data vectors



and pilot vectors



, transmitted over its channels, and the AWGN.

Looking carefully at the component dependent on

the pilot vectors, it becomes clear that it is made-up

N scaled replicas of each of the

n CIR,

corresponding to the

n channels that link the

transmit antennas with the considered receive

antenna. Moreover, the replicas of each CIR are

separated by

N samples and transmit antenna s

CIR replicas are time-shifted

samples from

the reference position

{

}

, 0, , 1

mN m N∈−

Figure 2 shows an example of a TD received

vector r



when 4

antennas transmit one

symbol carrying only pilots (data sub-carriers are not

loaded) over independent BRAN-A model multipath

channels (ETSI, 2001). The top plot represents the

overlapping of the signals from all transmit antennas

in one receive antenna. The four lower plots show

how the CIR replicas corresponding to each transmit

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

166

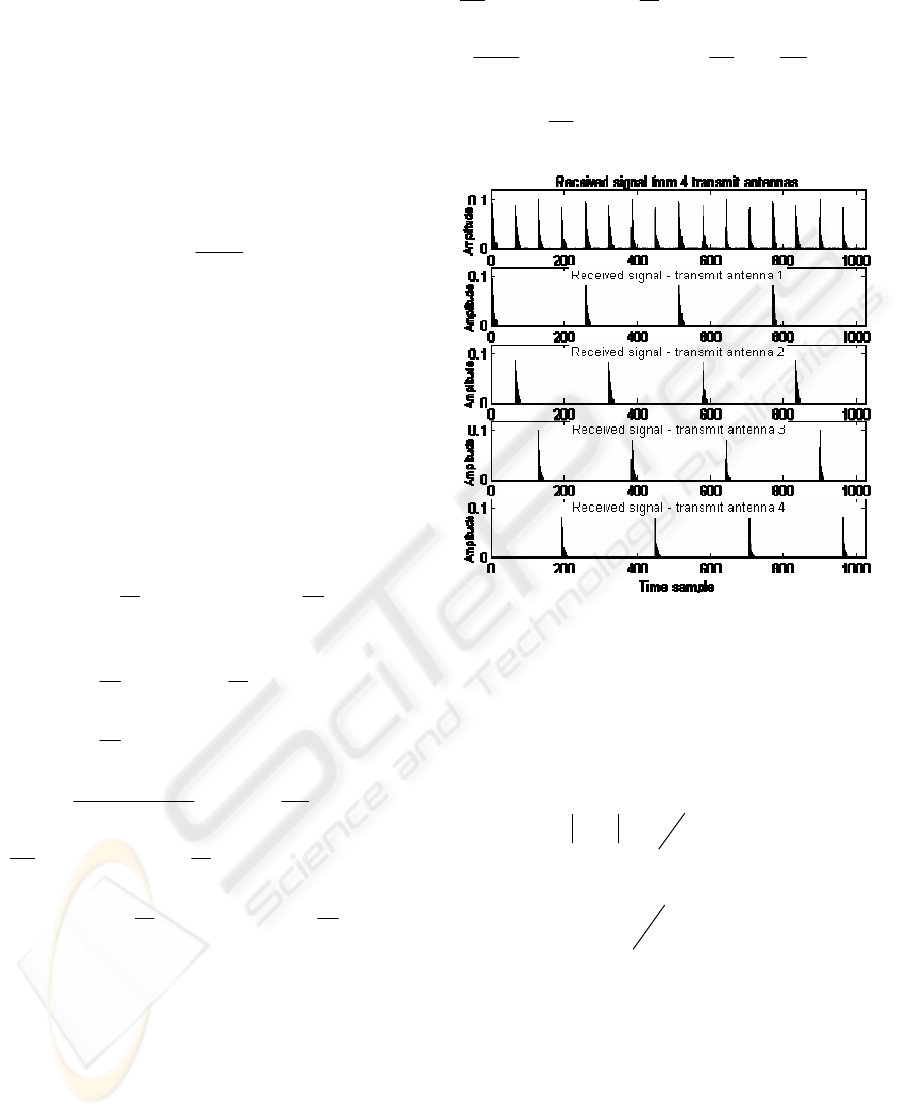
antenna are phase-shifted and can be separated from

the overall signal. It gives a clear image of the

condition that each CIR must fulfill so that

consecutive replicas do not overlap.

Given the transmit antenna s maximum channel

delay spread,

, and the system’s sampling

interval,

tΔ , the minimum pilot distance that can be

used without overlap of adjacent CIR replicas, thus

enabling the best performance of the channel

estimator, can be expressed as

≤

. (13)

As it will be demonstrated, if the condition in

(13) is verified the co-channel interference will be

eliminated. Otherwise, the overlapping of

consecutive replicas will cause distortion in the

estimation process and impose an MSE floor on the

estimate.

Considering that the condition presented by (13)

is fulfilled, the transmit antenna s CIR estimate

vector



can be obtained immediately from the TD

received vector



(Ribeiro, 2007),

[]

, 0,1, , 1

stt

rn N mN n

remaining

un un r n N mN

un un

hn mN lN

wn mN

−

−−

⎧

⎡⎤

+− = −

⎪

⎢⎥

⎨

⎣⎦

⎪

⎩

⎛⎞

⎡⎤⎡ ⎤

=−−+ +−

⎜⎟

⎢⎥⎢ ⎥

⎜⎟

⎣⎦⎣ ⎦

⎝⎠

⎛⎞

⎡⎤

=−−+×

⎜⎟

⎢⎥

⎜⎟

⎣⎦

⎝⎠

−−

⎡⎤

++−

⎢⎥

⎣⎦

∑

∑∑







[]

000

, 0,1, , 1

ss t t

msl

stt

hld n N mN l

hn wn N mN n

remaining

−

===

−

⎛⎞

⎜⎟

⎡⎤

⎜⎟

++−−

⎢⎥

⎜⎟

⎣⎦

⎝⎠

⎧

⎡⎤

++− = −

⎪

⎢⎥

⎨

⎣⎦

⎪

⎩

∑∑

∑∑∑

∑







,(14)

where

[

]

is the unit step function. The operation

in (14) estimates all

n CIR and must be repeated

for all

n receive antennas. The result in (14) is

possible because the data dependent component was

eliminated, considering that (Ribeiro, 2007),

[]

[] [ ]

000

00 0

exp

exp 0

ss t t

msl

sl k

Cf C S

hld n N mN l

hl d k j kn l

NN N n

jkmN

−

===

−−

−

== =

∉℘

−

⎡⎤

+−−=

⎢⎥

⎣⎦

⎡⎤

⎛⎞

=+−

⎢⎥

⎜⎟

⎢⎥

⎝⎠

⎣⎦

⎡⎤

×− =

⎢⎥

⎣⎦

∑∑∑

∑∑ ∑

∑





(15)

Figure 2: Decomposition of the combined received symbol

(pilots only) for

transmit antennas.

The CIR estimate resulting of (14) is the TD LS

equivalent of a SISO OFDM system (Ribeiro, 2007).

Consider a constant envelope modulation (though it

can be easily extended for any modulation) with

transmit power equally distributed among the

antennas,

[]

{

}

Esk

. Pilot and data sub-

carriers are transmitted with equal power. Assuming

that the noise in the TD samples is iid, the noise

variance in (14) is

, resulting in the channel

estimation MSE,

INI f

MSE N

. (16)

This initial estimate can be improved by

incorporating other TD algorithms at little or no

added computational load. With the knowledge that

the CIR energy is concentrated in a small set of taps,

the significant tap catching (STC) scheme (Li, 1999)

lowers the channel estimation MSE considerably.

Further improvement is provided by the TD linear

MIMO-OFDM CHANNEL ESTIMATION - A Pilot Sequence Design for Time-domain Processing

167

minimum MSE (LMMSE) filter (Edfors, 1996), if

the channel correlation and noise variance are

known a-priori (due to the CIR energy

concentration, the estimation of these parameter is

quite simpler in TD, when compared to FD).

Considering the more realistic approach of non-

sample-spaced channel (where channel paths are not

separated by multiples of

tΔ and energy leakage

occurs), other algorithms (Edfors, 1996) can provide

further improvement with added computational load.

3.1 Including the STC Algorithm

The CIR energy of wireless multipath channels is

commonly limited to a small set of taps. By

identifying this set of significant taps and ignoring

the remaining, we are removing noise from the

channel estimate, thus improving it (Li, 2002).

Considering the channel model introduced in

Section 2, the CIR will only have L significant taps.

Assuming that the set of significant taps is

{

}

, (14)

can be rewritten

[]

{}

[]

{}

stt

rn N mN n L

remaining

hn wn N mN n L

remaining

−

⎧

⎡⎤

+− ∈

⎪

⎢⎥

⎨

⎣⎦

⎪

⎩

⎧

⎡⎤

++−∈

⎪

⎢⎥

⎨

⎣⎦

⎪

⎩

∑



.(17)

By eliminating the noise in the non-significant

taps, the noise variance in (17) is reduced to

and the resulting channel estimation MSE

is,

Sf Sf

STC INI

nLN nLN

MSE MSE

. (18)

This MSE tends to the initial MSE when L goes

(limiting condition in (13)). The channel

estimation MSE achieved in (Li, 2002) is the same

as in (18) when

N = (training sequence).

The use of the STC algorithm actually lowers the

computational load by limiting the summation

interval. An error floor will limit the performance

for high values of SNR if the set

{}

is not properly

estimated and some CIR energy is removed.

3.2 Including TD LMMSE Filter

For low values of SNR, a significant improvement in

the channel estimation can be achieved by using the

TD LMMSE filter that minimizes the effect of the

noise in the estimate.

Considering the channel model introduced in

Section 2, where all channel taps are separated by

multiples of

, the TD MMSE filter is

implemented by a diagonal matrix (Edfors, 1996)

whose diagonal elements are defined by

[

]

[]



, where



is the CIR correlation

matrix. Because all paths of all channels are

uncorrelated, the matrix will only have L non-zero

values in the diagonal elements defined by

{

}

Therefore, the operation can be implemented

simultaneously with the operation in (13),

[]

[

]

[]

{}

[] []

[]

{}

rn N mN n L

nRn

remaining

nNmN

Rnhn w

remaining

−

⎧

⎡⎤

+− ∈

⎪

⎢⎥

⎨

⎣⎦

⎪

⎩

⎧

⎛⎞

⎡⎤

+−

⎪

⎜⎟

⎢⎥

⎜⎟

⎪

⎣⎦

⎝⎠

∈

⎨

⎪

⎩

∑





. (19)

The resulting channel estimation MSE (Edfors,

1996) is,

[

]

[]

{}

LMMSE

MSE

nLN

∈

∑



. (20)

Observing (20), we can conclude that when

SNR →∞,

MMSE STC

SE MSE→ .

The use of LMMSE filter lowers the

computational load by limiting the summation

interval but requires additional calculations to

estimate the channel correlation and noise variance.

For non-sample-spaced channels, the CIR

correlation is no longer a diagonal matrix and this

estimator no longer guaranties the MMSE criterion.

However it still is the best trade-off between

performance and computational load (Edfors, 1996).

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

168

0 5 10 15 20

-3

-2

-1

BER

Eb/N0 (dB)

Perfect CSI

TD LS

TD STC

TD MMSE

0 5 10 15 20

-3

-2

-1

BER

Eb/N0 (dB)

Perfect CSI

TD LS

TD STC

TD MMSE

Figure 3: System BER performance (BRAN-A indoor

channel).

Figure 4: System BER performance (BRAN-E outdoor

channel).

0 5 10 15 20

-35

-30

-25

-20

-15

-10

-5

ChEst MSE (dB)

Eb/N0 (dB)

TD LS

TD STC

TD MMSE

0 5 10 15 20

-35

-30

-25

-20

-15

-10

-5

ChEst MSE (dB)

Eb/N0 (dB)

TD LS

TD STC

TD MMSE

Figure 5: Channel estimation MSE (BRAN-A indoor

channel).

Figure 6: Channel estimation MSE (BRAN-E outdoor

channel).

4 SIMULATION RESULTS

A simulation scenario was implemented using an

Alamouti

21× OFDM system with 1024Nc

QPSK modulated sub-carriers, sampling interval

10tnsΔ= and a CP with 200 samples. The

transmitted OFDM symbols carried pilots and data

using the proposed pilot structure, with a pilot

separation

4Nf = .

The BRAN-A and BRAN-E channel models [14]

were used to simulate indoor (

50ns rms delay

spread) and outdoor environments (

250ns rms delay

spread), respectively.

To validate the proposed method, BER and

channel estimation simulations were performed,

using Eb/N0 values in the range of 0dB to 20dB. The

3 channel estimation schemes presented in section 3

were simulated with both channel models.

The BER results are depicted in

Figure 3 and

Figure 4, respectively for BRAN-A and BRAN-E

channels.

The normalized channel estimation MSE results

are depicted in Figure 5 and Figure 6, respectively

for BRAN-A and BRAN-E channels.

On both scenarios, the TD LS and the TD

MMSE methods present a consistent performance.

The TD LS method always achieves the worst

performance (

2dB

≈

degradation in the BER

compared with the perfect channel state information

– CSI) due to the fact that it does not take advantage

of the channel characteristics. In opposition, the TD

MMSE method always achieves the best

performance, near the ideal situation. It has the

ability of dealing with the increasing channel delay

spread by always weighing the energy of channel

taps vs. noise variance.

The performance of the TD STC method (Li,

2002) is closely dependent on the channel delay

spread. Its performance is bond by the 2 previous

methods. A channel with a short delay spread will

result in the best performance (by having the CIR

energy concentrated to just a few taps, most of the

noise is eliminated in the estimation process). As the

MIMO-OFDM CHANNEL ESTIMATION - A Pilot Sequence Design for Time-domain Processing

169

channel delay spread increases, the performance

tends to that of the TD LS method, with a significant

performance degradation.

5 CONCLUSIONS

We have presented a pilot sequence design and

associated channel estimation algorithms for MIMO-

OFDM systems, where all transmit antennas share

the same sub-carriers to convey pilot symbols. The

proposed design grants the receiver the ability of

extracting the CIRs by processing the antennas’ TD

received samples, without co-channel interference,

resulting in an algorithm with very low

computational load.

The investigated method presents a considerable

performance improvement when compared to the

method in (Li, 2002), especially in the more

demanding outdoor environments, where it shows

the ability of maintaining the performance despite

the increased channel delay spread.

ACKNOWLEDGEMENTS

The authors wish to thank Fundação para a Ciência e

a Tecnologia that partially supported this work

through the project “PHOTON - Distributed and

Extendible Heterogeneous Radio Architectures

using Fibre Optic Networks” (PTDC/EEA-

TEL/72890/2006).

REFERENCES

Nee, R. V., Prasad, R., 2000. OFDM for Wireless

Multimedia Communications, Artech House. 1

edition.

Stuber, G. L., Barry, J. R., McLaughlin, S. W., Li, Y.,

Ingram, M. A., Pratt, T. G., 2004. Broadband MIMO-

OFDM wireless communications. In Proceedings of

the IEEE, vol. 92, no. 2, pp. 271–294.

Sampath, H., Talwar, S., Tellado, J., Erceg, V., Paulraj,

A., 2005. A fourth-generation MIMO-OFDM

broadband wireless system design, performance, and

field trial results. In IEEE Communications Magazine,

pp. 143–149.

Paulraj, A. J., Gore, D. A., Nabar, R. U., Bolcskei, H.,

2004. An overview of MIMO communications - a key

to gigabit wireless. In Proceedings of the IEEE, vol.

92, no. 2, pp. 198–218.

Li, Y. G., Seshadri, N., Ariyavisitakul, S., 1999. Channel

estimation for OFDM systems with transmitter

diversity in mobile wireless channels. In IEEE Journal

on Selected Areas in Communications, vol. 17, no. 3,

pp. 461–471.

Li, Y. G., 2002. Simplified channel estimation for OFDM

systems with multiple transmit antennas. In IEEE

Transactions on Wireless Communications, vol. 1, pp.

67–75.

Shin, M., Lee, H., Lee, C., 2004. Enhanced channel-

estimation technique for MIMO-OFDM systems. In

IEEE Transactions on Vehicular Technology, vol. 53,

no. 1, pp. 261–265.

Zhang, H., Li, Y. G., Reid, A., Terry, J., 2005. Channel

estimation for MIMO-OFDM in correlated fading

channels. In IEEE International Conference on

Communications, pp. 2626-2630.

Zamiri-Jafarian, H., Pasupathy, S., 2007. Robust and

improved channel estimation algorithm for MIMO-

OFDM systems. In IEEE Transactions on Wireless

Communications, vol. 6, pp. 2106-2113.

Barhumi, I., Leus, G., Moonen, M., 2003. Optimal training

design for MIMO OFDM systems in mobile wireless

channels. In IEEE Transactions on Signal Processing,

vol. 51, pp. 1615-1624.

Minn, H., Al-Dhahir, N., 2004. Optimal training signals

for MIMO OFDM channel estimation. In IEEE Global

Telecommunications Conference, pp. 219-224.

Ribeiro, C., Gameiro, A., 2007. Direct time-domain

channel impulse response estimation for OFDM-based

systems. In IEEE Vehicular Technology Conference.

Edfors, O., 1996. Low-complexity algorithms in digital

receivers, Ph.D. dissertation, Lulea University of

Technology, Sweden.

ETSI TS 101 475 V1.2.2, 2001. Broadband Radio Access

Networks (BRAN): HIPERLAN Type 2: Technical

specification; Physical layer.

WINSYS 2008 - International Conference on Wireless Information Networks and Systems

170