
A LOCATION AND BANDWIDTH AWARE P2P VIDEO ON DEMAND
SYSTEM FOR MOBILE DEVICES
Danilo F. S. Santos and Angelo Perkusich
Embedded System and Pervasive Computing Laboratory, Department of Electrical Engineering
Federal University of Campina Grande, C.P. 10105 - 58109-970 - Campina Grande - PB - Brazil
Keywords:
Multimedia, Video on Demand, P2P Network.
Abstract:
Due the increasing number of new wireless technologies and the advent of new mobile devices, new services
and applications are necessary to supply the needs of these devices users. Video on-Demand (VoD) services
have become one of these services. In this paper we present a proposal of a P2P Mobile Video on-Demand
(VoD) System focused on mobile devices where they can act as both, media servers as well as clients. Due
to different possible communication interfaces that are available for mobile devices, we considered that they
can be in networks with different throughput characteristics, and also, they can be distributed through the
Internet. Therefore, our proposal make possible to build content distribution trees in the application layer
considering two major aspects related to mobility: the available bandwidth that the mobile device can share
with the network, and; the relative position of the mobile device in the network.
1 INTRODUCTION
In the last few years, the development of new wire-
less technologies and the advent of embedded mobile
devices, such as PDAs and smart phones, are grow-
ing rapidly. These new devices have embedded cap-
ture media devices, such as video cameras and audio
recorders, therefore, users can create multimedia con-
tent. Also, with the fast growing of peer-to-peer (P2P)
networks in the Internet (Wai-Pun Ken Yiu and Chan,
2007), users may share their content with other users.
As a result of this emerging scenario, new services
and applications are necessary to supply the needs
of the users. Video on-Demand (VoD) services have
become one of these services (Thouin and Coates,
2007). The main objective for VoD is to provide users
with the possibility to watch videos from the begin-
ning at any time.
In the context of mobile devices few works pro-
vide VoD services taking into account mobility re-
quirements. Most of the work related to VoD systems
(Hu, 2001) (Ma and Shin, 2002) relies on the use of
multicasting streams to share the video flow with the
maximum number of clients. However, due to the
nature of the Internet, multicasting is not a realistic
option.
Considering the issues mentioned above, in this
paper we present a proposal of a P2P VoD System fo-
cused on mobile devices where they can act as both,
media servers as well as clients. Thus, they can share
multimedia content, in the context of this paper video,
between nodes in an overlay network. Due to differ-
ent possible communication interfaces that are avail-
able for mobile devices, we considered that they can
be in networks with different throughput character-
istics, for instance a GPRS or a WLAN network,
and also, they can be distributed through the Internet.
Therefore, based on the proposal introduced in this
paper it is possible to build content distribution trees
in the application layer considering two major aspects
related to mobility: the bandwidth available that the
mobile device can share with the network, and; the
relative position of the mobile device in the network.
The rest of the paper is organized as follow. In
Section 2 we present a general overview of our pro-
posal, and describe the proposed tree algorithms. In
Section 3 we present a first analysis of the building
tree algorithms. Finally, the conclusion is presented
in Section 4.
2 PROPOSAL ARCHITECTURE
In this section we present a general overview of the
proposed architecture, focusing in the media distribu-
249
F. S. Santos D. and Perkusich A. (2008).
A LOCATION AND BANDWIDTH AWARE P2P VIDEO ON DEMAND SYSTEM FOR MOBILE DEVICES.
In Proceedings of the International Conference on Wireless Information Networks and Systems , pages 249-252
DOI: 10.5220/0002027702490252
Copyright
c
SciTePress

tion protocol and its main characteristics. In the de-
scription that follows we assume that a video V has a
duration D and is divided in T segments of D/T dura-
tion.
2.1 General Overview
The proposed P2P VoD system is divided in two over-
lay networks:
• The control network, which is responsible for
the communication between client nodes and the
server node that stores the original content. For
the architecture a P2PSIP based network is pro-
posed (iet, 2007).
• The distribution network, which is responsible to
distribute the content (video segments) between
the nodes using point-to-point connections in a
P2P based way. The content is distributed using
a single source application layer tree, then using a
different overlay network than the previous one.
The option to use two different overlay networks
was done to make possible use other mechanisms (be-
yond SIP) to control the distribution network. This
approach is shown in Figure 1.
Figure 1: Overall Architecture.
2.2 Obtaining Network Information
In the proposal presented in this paper it is necessary
to collect network context information to distribute
the media content between mobile nodes. Specifi-
cally, our building algorithm relies on two types of in-
formation: the Available Bandwidth and the Position
information. To collect this information, we propose
the use of two widely-used and light-weight tools:
• Vivaldi algorithm (Dabek et al., 2004) to calculate
the relative coordinates of the host in the network;
• Pathload (Jain and Dovrolis, 2002) tool to esti-
mate the available bandwidth of a path.
2.3 Forming the Distribution Tree
After receive all requests of one layer, the server node
arranges the incoming nodes in a single source tree
application layer. We propose three tree building al-
gorithms:
• A simple bandwidth aware algorithm;
• A bandwidth and position aware algorithm;
• A fast bandwidth and position aware algorithm.
2.3.1 Simple Bandwidth Aware Tree - SBA
This algorithm is based on the Breadth-First Search
algorithm (Knuth, 1997). It uses two data struc-
tures: one which holds nodes not visited by the algo-
rithm (whiteList ), and other that holds visited nodes
but without adjacent (children) nodes (grayList). The
nodes that have already been visited and have children
nodes are called black nodes.
The algorithm starts inserting the source node in
the grayList, initializing all other nodes with it dis-
tance from the source dsrc as infinity and adding those
in the whiteList. It proceeds by getting one node X
from the grayList. Node X share bandwidth to support
other N nodes as it children. These N nodes are in-
serted in the grayList and removed from the whiteList.
Node X is set as a black node. The operation is re-
peated until the grayList is empty, so until all nodes
are visited and have assigned nodes as children, if
possible. This algorithm is showed in the following
pseudo code.
Listing 1: SBA Pseudo Code.
1 SBA( AllNo d es , sr c N o d e )
2 f o r e a c h n o d e n i n Al lN od es :
3 c o l o r [ n ] : = WHITE
4 d s r c [ n ] : = i n f i n i t y
5 end f o r
6 c o l o r [ s r c N o d e ] : = GRAY
7 d s r c [ src No de ] : = 0
8 p u sh ( g r a y L i s t , sr c N o d e )
9 w h i l e ( g r a y L i s t != 0 )
10 u : = p u l l F i r s t ( g r a y L i s t )
11 fo r i = 1 t o N[ u ] :
12 n : = p u l l F i r s t ( w h i t e L i s t )
13 c o l o r [ n ] : = GRAY
14 p a r e n t [ n ] : = u
15 d s r c [ n ] : = d s r c [ u ] + 1
16 pu s h ( g r a y L i s t , n )
17 end f o r
18 c o l o r [ u ] : = BLACK
19 end w h i l e
2.3.2 Bandwidth and Position Aware Tree - BPA
This algorithm is based on the Dijkstra’s algorithm
(Dijkstra, 1959). It uses three data structures, the
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
250

same two structures described in the previous algo-
rithm (whiteList and grayList), and also a list that hold
gray nodes with available bandwidth to support other
children (almostBlackList).
The algorithm starts inserting the source node in
the grayList, initializing all other nodes with it dis-
tance from the source dsrc as infinity and adding
those in the whiteList. It proceeds by getting (and
removing) the closest node X to the source from the
grayList. This node is inserted in the almostBlack-
List. Then, for each node in the grayList and whiteList
(let’s merge these two lists in one whiteAndGrayList)
it is calculated the new distance from the source ele-
ment through each element in almostBlackList. This
is the “relax” process of the Dijkstras algorithm. All
visited nodes are inserted (or updated) in the grayList.
Listing 2: BPA Pseudo Code.
1 BPA( ALLNodes , s rc No de )
2 f o r e a c h n o d e n i n ALLNodes :
3 d s r c [ n ] : = i n f i n i t y
4 c o l o r [ n ] : = WHITE
5 end f o r
6 c o l o r [ s r c N o d e ] : = GRAY
7 d s r c [ src No de ] : = 0
8 i n s e r t ( g r a y L i s t , sr c N o d e )
9 w h i l e ( g r a y L i s t != 0 )
10 u : = e x t r a c t −min−d s r c ( g r a y L i s t )
11 al m o s t B l a c k : = a l m o s t B l a c k U {u }
12 p : = p a r e n t [ u ]
13 i f p i s n o t u :
14 N[ p ] : = N[ p ] − 1
15 i f N[ p ] = 0 :
16 rem o v e [ a l m o s t B l a c k , p ]
17 c o l o r [ p ] : = BLACK
18 fo r e ac h node v i n w h i t e A n d G r a y L i s t :
19 i f p a r e n t [ v ] = p :
20 f o r e a c h n o d e b i n a l m o s t B l a c k :
21 RELAX( b , v )
22 end f o r
23 end f o r
24 e l s e
25 f o r e a ch node v i n wh i t e A n d G r a y L i s t :
26 RELAX( u , v )
27 en d f o r
28 end w h i l e
29
30 RELAX( u , v )
31 i f ( d i s t a n c e O f ( u , v ) + d s r c [ u ] < d s r c [ v ] )
32 d s r c [ v ] : = d i s t a n c e O f ( u , v ) + d s r c [ u ]
33 p a r e n t [ v ] : = u
34 i f ( c o l o r [ v ] = WHITE)
35 c o l o r [ v ] : = GRAY
36 i n s e r t ( g r a y L i s t , v )
37 e l s e
38 u p d a t e ( g r a y l i s t , v )
When one node in the almostBlackList uses all N
connections (do not support more children), then it
is removed from that list and all nodes in the white-
AndGrayList must update its dsrc information (relax
process). We check this every time a parent is as-
signed to a node. The operation is repeated until the
grayList is empty. This algorithm is described in the
following pseudo code.
2.3.3 Fast Bandwidth and Position Aware Tree -
FBPA
This algorithm is based on the first algorithm pre-
sented, but using the “relax” process of the previous
algorithm. Therefore, it uses two data structures, the
whiteList and grayList.
As the previous algorithms, this one starts insert-
ing the source node in the grayList, initializing all
other nodes with it distance from the source dsrc as
infinity and adding those in the whiteList. It pro-
ceeds by extracting the closest node X to the source
node from the grayList. Node X share bandwidth to
provide other N nodes as it children. For all nodes
in the whiteList it is calculated the distance from X.
Then, the N closest nodes from X are inserted in the
grayList. Node X is set as a black node. The operation
is repeated until the grayList is empty. This algorithm
is described in the following pseudo code.
Listing 3: FBPA Pseudo Code.
1 FBPA ( AllN o des , sr cN od e )
2 f o r e a c h n o d e n i n Al lN od es :
3 c o l o r [ n ] : = WHITE
4 d s r c [ n ] : = i n f i n i t y
5 end f o r
6 c o l o r [ s r c N o d e ] : = GRAY
7 d s r c [ src No de ] : = 0
8 p u sh ( g r a y L i s t , sr c N o d e )
9 w h i l e ( g r a y L i s t != 0 )
10 u : = p u l l F i r s t ( g r a y L i s t )
11 fo r e ac h node v i n w h i t e L i s t :
12 d s r c [ v ] : = d i s t a n c e O f ( u , v ) + d s r c [ u ]
13 end f o r
14 fo r i = 1 t o N[ u ] :
15 n : = e x t r a c t −min−d s r c ( w h i t e L i s t )
16 c o l o r [ n ] : = GRAY
17 p a r e n t [ n ] : = u
18 pu s h ( g r a y L i s t , n )
19 end f o r
20 c o l o r [ u ] : = BLACK
21 end w h i l e
3 PRELIMINARY ANALYSIS
In this section we analyze the three building algo-
rithms, comparing the mean distance from the source
node against the elapsed time during the calculation
of the tree. The nodes were inserted in a network
topology and its coordinates were normalized to be
in a Cartesian plan between (0,0) and (1000,1000).
Also, the nodes could share their bandwidth with
A LOCATION AND BANDWITDH AWARE P2P VIDEO ON DEMAND SYSTEM FOR MOBILE DEVICES
251
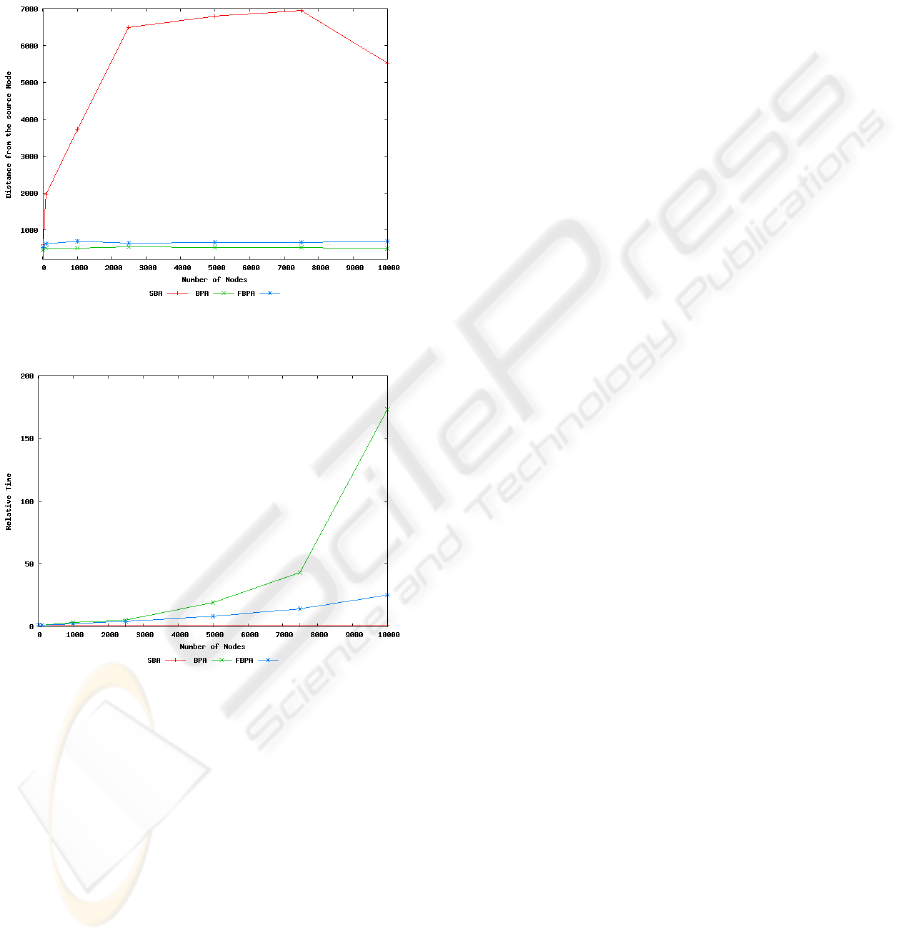
a maximun of three others nodes. The simulations
were done using topologies with 10, 100, 1000, 2500,
5000, 7500 and 10000 nodes. The first graph on Fig-
ure 2 shows the mean distance from the source for
each topology. The second graph on Figure 3 shows
the relative elapsed time to calculate the tree for each
topology. This elapsed time is relative to the calcula-
tion time of SBA, which is the fastest one.
Figure 2: Mean distance from the source node.
Figure 3: Relative calculation elapsed time.
Despite of the fact that the mean distance of BPA
is shorter than FBPA, the relative elapsed time when
calculate a tree with more than 1000 nodes of the BPA
grows faster than the elapsed time of FBPA. Then,
when calculating the distribution tree, a tradeoff be-
tween the number of nodes and complexity of the al-
gorithm must be considered. Especially when dealing
with a big amount of nodes (more than 1000), and
nodes with restricted processing capabilities, such as
mobile devices.
4 CONCLUSIONS
In this paper we presented an architecture for a mobile
P2P Video on-Demand system, which uses the avail-
able bandwidth and position information of the nodes
to efficiently distribute the multimedia content. It was
discussed why use two overlay networks, one for the
control and negation between the nodes, and another
to distribute the content.
Also, we have shown three tree building algo-
rithms that take into account both, the available band-
width as well as the position information of the nodes
to build trees with low mean distance from the source.
We compared the algorithms considering the process-
ing time to calculate the tree, and the mean distance
from the source of each node. We have shown that
a tradeoff between the BPA (Bandwidth and Position
Aware Tree) and FBPA (Fast Bandwidth and Position
Aware Tree) algorithms must be considered related to
the number of nodes in each calculation.
The next step in our work is the simulation of the
system as a whole in a more realistic topology. In this
simulation we intend to analyze the delay for video
delivery. Also, we plan to simulate others cases, such
as changes of available bandwidth of a node during
a transmission, leave of a node, failure of a node,
change in the position of a node, and other specific
cases. Finally, after the simulation stage, a full imple-
mentation of the system is planned in order to validate
the system as a whole.
REFERENCES
(2007). IETF P2PSIP Working Group.
Dabek, F., Cox, R., Kaashoek, F., and Morris, R. (2004).
Vivaldi: A decentralized network coordinate system.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische Mathematik.
Hu, A. (2001). Video-on-demand broadcasting protocols:
a comprehensive study. In Proceedings. INFOCOM
2001. Twentieth Annual Joint Conference of the IEEE
Computer and Communications Societies, pages 508
– 517. IEEE.
Jain, M. and Dovrolis, C. (2002). Pathload: A measurement
tool for end-to-end available bandwidth.
Knuth, D. E. (1997). The Art Of Computer Programming.
Ma, H. and Shin, K. G. (2002). Multicast video-on-
demand services. SIGCOMM Comput. Commun. Rev.,
32(1):31–43.
Thouin, F. and Coates, M. (2007). Video-on-demand
networks: Design approaches and future challenges.
IEEE Network, 21:42 – 48.
Wai-Pun Ken Yiu, X. J. and Chan, S.-H. G. (2007). Chal-
lenges and approaches in large-scale peer-to-peer me-
dia streaming. In IEEE Multimedia, Vol. 14, No. 2,
pages 50–59.
WINSYS 2008 - International Conference on Wireless Information Networks and Systems
252
