Comparing Two Action Planning Approaches for Color

Learning on a Mobile Robot

Mohan Sridharan and Peter Stone

The University of Texas at Austin, USA

Abstract. A major challenge to the deployment of mobile robots in a wide range

of tasks is the ability to function autonomously, learning appropriate models for

environmental features and adapting these models in response to environmental

changes. Such autonomous operation is feasible iff the robot is able to plan an

appropriate action sequence. In this paper, we focus on the task of color model-

ing/learning, and present two algorithms that enable a mobile robot to plan action

sequences that facilitate color learning. We propose a long-term action-selection

approach that maximizes color learning opportunities while minimizing localiza-

tion errors over an entire action sequence, and compare it with a greedy/heuristic

action-selection approach that plans incrementally, to maximize the utility based

on the current state information. We show that long-term action-selection pro-

vides a more principled solution that requires minimal human supervision. All

algorithms are fully implemented and tested on the Sony AIBO robots.

1 Motivation

Recent developments in sensor technology have provided a range of high-ﬁdelity sen-

sors (laser range ﬁnders, color cameras) at moderate costs, thereby making it feasible

to use mobile robots in several ﬁelds [1–3]. But the sensors typically require frequent

and extensive manual calibration in response to environmental changes. An essential

requirement for the widespread deployment of mobile robots is therefore the ability

to function autonomously, learning appropriate models for environmental features, and

adapting these models in response to changes in the environment. Such autonomous

behavior can be achieved iff the mobile robot can autonomously plan a sequence of

actions that facilitates learning and adaptation. Mobile robots typically operate under

constrained computational resources, but they need to operate in real-time to respond

to the dynamic changes in their environment. Autonomous learning and adaptation on

mobile robots is hence a challenging problem.

Here we focus on autonomous learning and adaptation in the context of color seg-

mentation, i.e. the mapping from image pixels to color labels such as red, blue and or-

ange. This mapping, called the color map, may require extensive manual re-training in

response to environmental changes such as illumination and object conﬁgurations. We

enable the robot to autonomously plan an action sequence that facilitates color learning,

which can be combined with prior work that adapts to illumination changes [4].

Traditional approaches to planning [5–7] require that all the actions and their ef-

fects be known in advance, along with extensive knowledge of state and/or all possible

contingencies. Mobile robots operate with noisy sensors and actuators, and typically

Sridharan M. and Stone P. (2008).

Comparing Two Action Planning Approaches for Color Learning on a Mobile Robot.

In VISAPP-Robotic Perception, pages 43-52

DOI: 10.5220/0002337300430052

 SciTePress

possess incomplete knowledge of the world state and the results of their actions. Here

the robot autonomously builds probabilistic models of the effects of their actions. These

models are used to plan action sequences that maximize color learning opportunities

while minimizing localization errors over the entire sequence. We compare this long-

term action-planning with a typical greedy approach that uses human-speciﬁed heuris-

tics to model the possible results of actions, and plans actions incrementally (one step

at a time) to maximize gain given the current state of the world. We show (Section 5)

that long-term action-planning is more robust than the greedy approach.

2 Related Work

Color segmentation and color constancy are well-researched sub-ﬁelds of computer

vision [8–11], though the approaches are computationally expensive to implement on

mobile robots with constrained resources.

The color map is typically created on mobile robots by hand-labeling image regions

over a few hours [12]. Cameron and Barnes [13] learn this mapping by constructing

closed image regions corresponding to known environmental features. The pixels from

these regions are used to build classiﬁers, but the approach requires human supervi-

sion and ofﬂine processing. Jungel [14] maintains layers of color maps with increasing

precision levels, colors being represented as cuboids. But the segmentation is not as ac-

curate as the hand-labeled one. Schulz and Fox [15] estimate colors using a hierarchical

Bayesian model with Gaussian priors and a joint posterior on robot position and illumi-

nation; the approach requires extensive prior information even for testing under two il-

luminations. Anzani et al. [16] model colors using a mixture of Gaussians and compen-

sate for minor illumination changes. But the method requires prior knowledge of color

distributions and suitable parameter initialization. Thrun et al. [3] distinguish between

safe and unsafe road regions, modeling colors as a mixture of Gaussians whose param-

eters are updated using EM. The approach does not help distinguish between overlap-

ping colors. Our prior work enables the robot to detect large illumination changes, and

learn colors through planning using human-speciﬁed heuristic functions [4]. Research

in planning on mobile robots has lead to several approaches [5–7], which typically re-

quire manual description of the possible states that the robot can be in and/or the effects

of the actions that the robot can execute. Here we enable the robot to learn probabilistic

models that predict the results of actions, and generate complete action sequences that

maximize color learning opportunities while minimizing localization errors.

3 Experimental Platform and Color Model

The experiments were run on the SONY ERS-7 Aibo, a four-legged robot whose pri-

mary sensor is a CMOS color camera with a limited ﬁeld-of-view (56.9

horz., 45.2

vert.). The images are captured at 30Hz with a resolution of 208×160 pixels. The robot

has three degrees-of-freedom in each leg and three in its head. All processing for vision,

localization, motion and strategy is done using an on-board 576MHz processor.

Applications on mobile robots with cameras typically involve a color calibration phase

that is repeated when the environment changes. An application domain for Aibos is the

4444

RoboCup Legged League [17], where teams of four robots play a competitive game

of soccer on an indoor ﬁeld (see Figure 1). We compare two schemes for autonomous

color learning.

Fig.1. Image of Aibo and ﬁeld.

3.1 Color Map and Model

In order to operate in a color coded environment, the robot needs a color map that

provides a discrete color label for each point in the color space:

Π : { m

1,i

, m

2,j

, m

3,k

} 7→ l |

l∈[0,N −1]

, ∀i, j, k ∈ [0, 255] (1)

where m

, m

are the values along the color channels (e.g. R, G, B) and l refers to

the numerical indices of the color labels (blue, orange etc). Typically, the color map is

obtained by generalizing from samples provided by a human observer who labels spe-

ciﬁc image regions (≈ 30 images) over a period of an hour or more [12]. We compare

two action-selection algorithms that enable autonomous color learning: (a) a long-term

approach that maximizes learning opportunities while minimizing localization errors

over the entire action sequence, and (b) a greedy approach that plans one action at time,

maximizing gain based on manually-tuned heuristics and the current state of the world.

Both planning schemes generate a sequence of poses (x, y, θ) that the robot moves

through, learning one color at each pose. We assume that the robot can use the known

structure of the environment (positions, shapes and color labels of objects of interest)

to extract suitable image pixels at each pose, and model the color distributions. As

described in our prior work [4], each color distribution is modeled as a 3D Gaussian or

as a 3D histogram (normalized to obtain a pdf), the choice being made autonomously

for each color, based on statistics collected in real-time. The color space is discretized

and each color map cell is assigned the label of the most likely color’s pdf, by a Bayes’

rule update.

4 Planning Algorithms

In both action-selection algorithms for color learning, the robot starts out with no prior

information on color distributions – the illumination is assumed to be constant during

learning. The robot knows the positions, shapes and color labels of objects in its envi-

ronment (structure)

, and its starting pose. The robot’s goal is to plan a action sequence,

Approaches exist for learning this structure autonomously.

4545

extract suitable image pixels at each pose, learn a model for the color distributions, and

generate the color map to be used for segmentation, object recognition and localization.

4.1 Long-term Planning

Algorithm 1 presents the long-term planning approach, which aims to maximize learn-

ing opportunities while minimizing errors over the motion sequence – the robot may

obtain more training samples by moving a larger distance, but this motion may cause

larger localization errors. Three components are introduced: a motion error model, a

statistical feasibility model, and a search routine.

Algorithm 1 Long-term Action-Selection.

Require: Ability to learn color models [4].

Require: Positions, shapes and color labels of the objects of interest in the robot’s environment

(Regions). Initial robot pose.

Require: Empty Color Map; List of colors to be learned - Colors.

1: Move between randomly selected target poses.

2: CollectMEMData() – collect data for motion error model.

3: CollectColLearnStats() – collect color learning statistics.

4: NNetTrain() – Train the Neural network for the MEM, Equation 2.

5: UpdateFM() – Generate the statistical feasibility model, Equation 3.

6: GenCandidateSeq() – Generate candidate sequences, Equation 4.

7: EvalCandidateSeq() – Evaluate candidate sequences.

8: SelectMotionSeq() – Select ﬁnal motion sequence.

9: Execute motion sequence and model colors [4].

10: Write out the color statistics and the Color Map.

Motion Error Model (MEM). The MEM predicts the error in the robot pose in re-

sponse to a motion command (target (x, y, θ)), as a function of the colors used for

localization (the locations of color-coded markers are known). Assuming an even dis-

tribution of objects in the environment, the inputs are the difference between the starting

pose and target pose, and the list of colors the robot has already learned. The output is

the pose error that would be incurred during this motion. The MEM is represented as

a back-propagation neural network [18] with N + 3 inputs, three outputs and a hidden

layer of 15 nodes:

{∆

, ∆

, c

, . . . , c

} 7→ {err

, err

} (2)

where {∆

, ∆

} represent the desired difference in pose, and {c

, c

, . . . , c

} are

binary variables that represent the N colors in the environment. If the robot knows all

the colors it can recognize all the markers and localize well. With only some colors

known, some markers aren’t recognizable and localization suffers. During training the

robot moves between randomly chosen poses running two localization routines, one

with all colors known (to provide ground truth), and another with only a subset of

colors known. The difference in the two pose estimates provides the outputs for training

samples.

4646

Statistical Feasibility Model (FM). For each robot pose, the FM provides the proba-

bility of learning each of the desired colors given that a certain set of colors have been

learned previously. The possible robot poses are discretized into cells. Given the robot’s

joint angles and camera ﬁeld-of-view, a feasibility check eliminates several cells – if the

robot’s camera is not pointing towards a valid object it cannot learn colors. Each FM

cell also stores a probability:

F M (d, e, f, v

) = p, ∀{d, e , f} ∈ [0, K − 1] (3)

where d, e, f are cell indices corresponding to the K discrete poses (x, y, θ), and v

, i ∈

[0, M − 1] represents all possible combinations of colors. As the robot moves during

training, its pose maps into one of the cells. Assuming prior knowledge of a set of

colors, it attempts to learn other colors and stores a count of successes. At the end of

the training phase, the normalized cell counts provide the probability.

Search for Motion Sequence. In the training phase the robot moves between ran-

domly chosen target poses and collects the data/statistics to build the MEM (lines 2, 4)

and the FM (lines 3, 5). The FM has to be re-learned when the object conﬁgurations

change, but even with just the geometric constraints the robot is able to provide motion

sequences leading to successful color learning. Then the robot iterates through all can-

didate motion sequences (GenCandidateSeq – line 6), i.e. all possible paths through the

discretized pose cells. The search depth is equal to the number of colors to be learned

i.e. to learn N colors:

path : {x

, y

, θ

, c olor

} ∀i ∈ [0, N − 1] (4)

This formulation results in a large number of paths (≈ 10

). But only a much smaller

subset (≈ 10

) is evaluated completely. The MEM provides the expected pose error if

the robot travels from the starting pose to the ﬁrst pose. The vector sum of the error

and the target pose provides the actual pose. If the desired color can be learned at this

pose (evaluated using FM), the move to the next pose in the path is evaluated. If the

whole path is evaluated, the net pose error and probability of success are computed

(EvalCandidateSeq – line 7). Of the paths that provide a high probability of success,

the one with the least pose error is executed by the robot (SelectMotionSeq – line 8) to

extract suitable image pixels and learn the parameters of the color models [4].

4.2 Greedy Action Planning

Algorithm 2 describes greedy action-selection. Actions are planned one step at a time,

maximizing utility based on current state knowledge. The main difference compared to

Algorithm 1 is that the functions that predict the results of actions are manually tuned

and heuristic, as with typical planning approaches [7]

Due to the noise in the motion model and the initial lack of visual information,

geometric constraints on object positions are used to resolve conﬂicts during learning.

The robot needs to decide the order in which the colors are to be learned, and the best

candidate object for learning a color. The algorithm makes these decisions greedily and

We assume that the robot learns one color at each pose.

4747

Algorithm 2 Greedy Action-Selection.

Require: Ability to learn color models [4].

Require: Positions, shapes and color labels of the objects of interest in the robot’s environment

(Regions). Initial robot pose.

Require: Empty Color Map; List of colors to be learned - Colors.

1: i = 0, N = M axColors

2: while i < N do

3: Color = BestColorToLearn( i );

4: T argetP ose = BestTargetPose( Color );

5: Motion = RequiredMotion( T argetP ose )

6: Perform Motion {Monitored using visual input and localization}

7: Model the color [4] and update color map.

8: i = i + 1

9: end while

10: Write out the color statistics and the Color Map.

heuristically – it uses heuristic action models to plan one step at a time. The aim is to

obtain a large target object while moving minimally, especially when not many colors

are known. Three weights are computed for each color-object combination (l, i):

= f

( d(l, i) ), w

= f

( s(l, i) ), w

= f

( o(l, i) ) (5)

where the functions d(l, i), s(l, i) and o(l, i) represent the distance, size and object

description for each color-object combination. Function f

( d(l, i) ) assigns a smaller

weight to larger distances – the robot should move minimally to learn the colors. Func-

tion f

( s(l, i) ) assigns larger weights to larger candidate objects – larger objects pro-

vide more samples (pixels) to learn the color parameters. Function f

( o(l, i) ) assigns

larger weights iff the particular object (i) for a particular color (l) is unique, i.e. it can

be used to learn the color without having to wait for any other color to be learned. In

each planning cycle, the robot uses the weights to dynamically chooses the color-object

combination that provides the highest value. The BestColorToLearn (line 3) is:

argmax

l∈[0,9]



max

i∈[0,N

−1]

{ f

( d(l, i) ) + f

( o(l, i) ) }



(6)

where the robot parses the different objects (N

) available for each color (l ∈ [0, N −1])

– the color with the maximum value is chosen to be learned ﬁrst. The robot determines

the best target object to learn that color as:

argmax

i∈[0,N

−1]



( d(l, i) ) + f

( o(l, i) )



(7)

For a chosen color, the target object provides the maximum weight/value. The robot

then computes the target pose where it can learn from this target object, based on the

known ﬁeld-of-view constraints (line 5). The robot executes the motion command to

move to the target pose, extract suitable image pixels and model the color’s distribution

(lines 6-7). The known colors are used to recognize objects, localize, and provide feed-

back, i.e. the knowledge available at any given instant is exploited to plan and execute

the subsequent tasks.

4848

5 Experimental Setup and Results

We ran experiments to compare the two action-selection algorithms in the robot soccer

domain. We aim to ensure that the learned color map is similar in performance to a

hand-labeled color map. But segmentation accuracy is not a good performance mea-

sure in the presence of background noise. Hence the localization accuracy is measured.

Of the colors needed for localization (pink, yellow, blue, white, green), the ground col-

ors (green, white) are typically learned/modeled by scanning in place (a feature of the

environment) – the depth of the search process is therefore three. The algorithms ex-

tend to additional colors, the smaller subset being used only to make things easier to

understand.

For long-term action-selection, the range of poses was divided into (6×9×12) cells,

i.e. divisions of 600mm, 600mm, and 30

along x, y, amd θ. The back-propagation net-

work was learned using the MATLAB Neural Network toolbox [19] (≈ 2000 training

samples). For the greedy action-selection scheme, the heuristics were modeled as linear

and exponential functions (Equation 5) whose parameters were experimentally tuned.

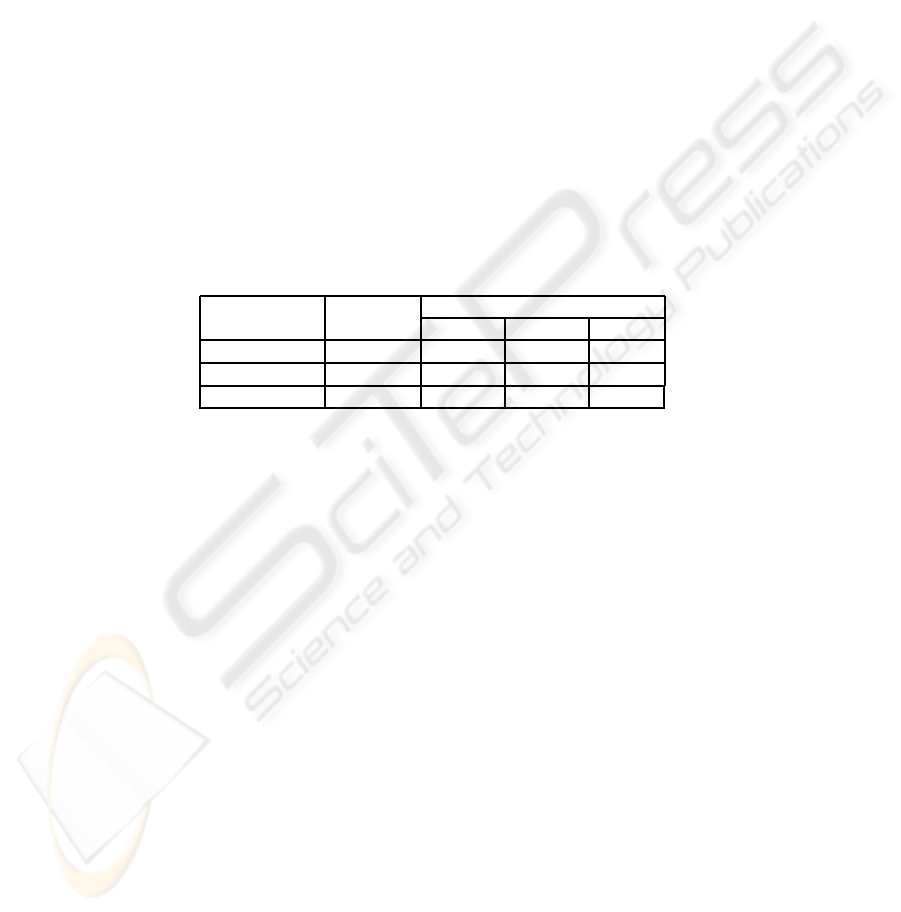
Table 1. Planning and Localization Accuracies in challenging conﬁgurations with two planning

schemes. Long-term planning is better.

Conﬁg Plan success Localization error

X (cm) Y (cm) θ (deg)

Long-term 100 7.6 ± 3.7 11.1 ± 4.8 9 ± 6.3

Greedy heuristic 89.3 ± 6.7 11.6 ± 5.1 15.1 ± 7.8 11 ± 9.7

Hand-label n/a 6.9 ± 4.1 9.2 ± 5.3 7.1 ± 5.9

Both algorithms were tested under several object conﬁgurations and robot starting

poses – there are six objects that can be placed anywhere along the outside of the ﬁeld,

but the robot knows their positions. Table 1 shows the success ratio averaged over 5

different object conﬁgurations, each with 15 different robot starting poses – a trial is

a success if all desired colors are learned. We also had the robot move through a set

of poses using the learned color map and measured localization errors (15 trials of 10

poses each) – a tape measure and protractor provided ground truth (see Table 1).

With long-term planning, the robot is able to generate a valid plan over all the tri-

als, unlike in the case with human-speciﬁed heuristics. The localization accuracy with

long-term planning is better than that with greedy planning, and is comparable to that

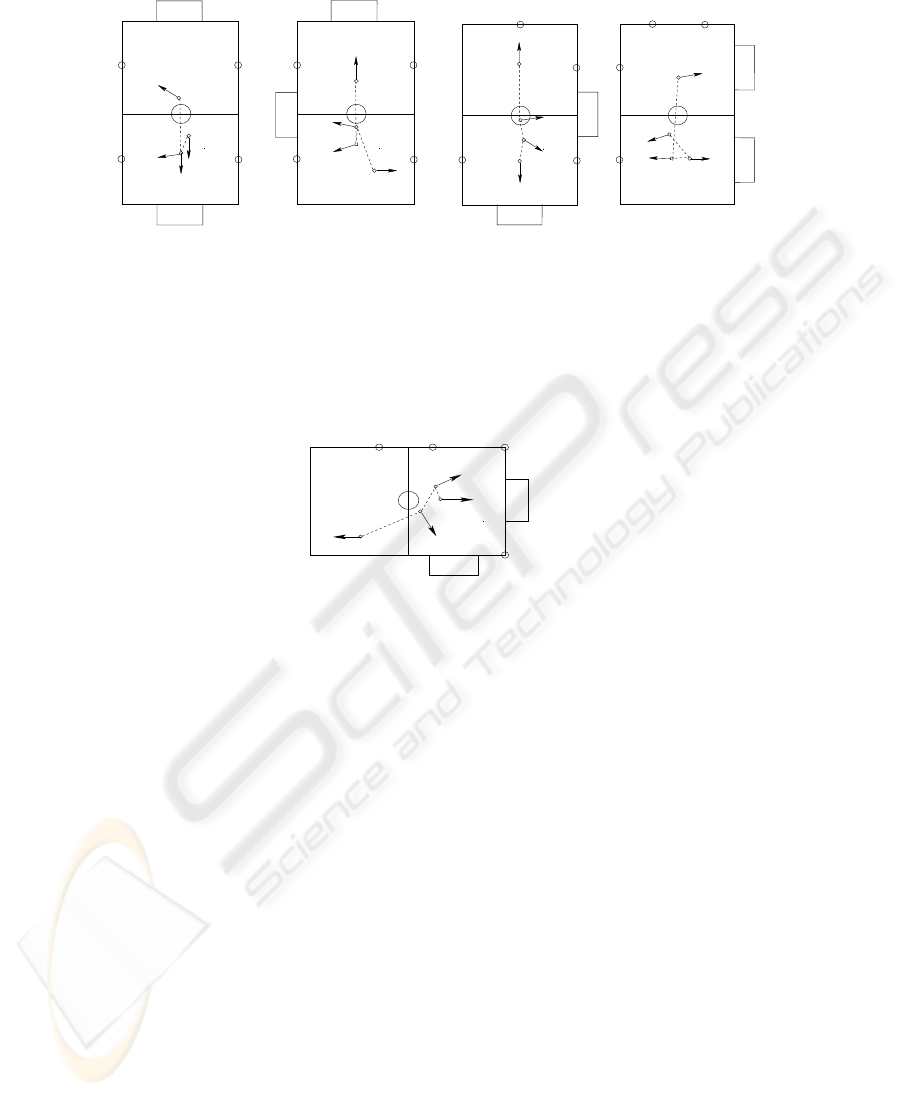
obtained with a hand-labeled color map. Figure 2 shows some plans obtained with our

long-term planning scheme, the starting position denoted by number ’0’, while the di-

rection of the arrows show the orientation. We observe:

1. As all objects with the color pink have another colored blob of the same size,

the robot learns pink only after one of the other two colors (blue, yellow) have been

learned.

2. Among the other two colors (blue, yellow) the robot ﬁrst learns the color which

requires motion that would result in smaller localization error.

3. For colors which exist in several objects the robot automatically makes a trade-

off between object size and distance to be moved.

4949

PINK−BLUE

BLUE−PINK

PINK−YELLOW

YELLOW−PINK

BLUE−PINK

YELLOW−PINK

BLUE GOAL

YELLOW GOAL

PINK−YELLOW

PINK−BLUE

BLUE GOAL

PINK−BLUE

BLUE GOAL

BLUE−PINK

YELLOW−PINK

YELLOW GOAL

PINK−YELLOW

PINK−BLUE

BLUE−PINK

PINK−YELLOW

YELLOW−PINK

YELLOW GOAL

BLUE GOAL

Fig.2. Sample motion plans generated by long-term planning. All plans lead to successful learn-

ing on the robot.

In addition to the ’best’ motion-plan, several of the top sequences lead to successful

learning. The algorithm works well when additional colors that overlap with existing

colors (orange, red etc) are also learned.

PINK−BLUE

YELLOW GOAL

BLUE GOAL

BLUE−PINK

YELLOW−PINK

PINK−YELLOW

Fig.3. A conﬁguration where heuristic planning fails.

The reason behind the better performance of the long-term planning algorithm, as com-

pared to the heuristic planning scheme, is determined by analyzing the conﬁgurations

where the heuristic planning failed to work. Figure 3 shows one example, where the

robot has to move a large distance to obtain its ﬁrst color-learning opportunity (from

pose 0 to 1). This sometimes leads the robot into poses different from its target pose

(pose 1) due to slippage, and it is then unable to ﬁnd any candidate image region that

satisﬁes the constraints for the target. Autonomous learning of models for motion errors

and color learning feasibility enables long-term planning to anticipate pose estimation

errors and account for it in the learning procedure. The long-term planning scheme fails

only due to unforeseen reasons (say the environment changes after a plan is created).

Then the robot replans a path starting from current state – the learned MEM and FM

are still applicable.

The color learning with either planning approach proceeds autonomously in real-

time: long-term planning takes ≈ 7 minutes, while greedy planning takes ≈ 6 minutes

of robot effort – hand-labeling takes ≈ 2 hours of human effort. The additional time

taken by the long-term planning scheme is due to the initial search for the motion se-

quence. The initial training of the models (in long-term planning) takes 1-2 hours, but it

proceeds autonomously (human supervision only for changing batteries), and needs to

be done only once for an environment. The greedy planning scheme, on the other hand,

5050

requires manual parameter tuning of heuristics (over a few days), which is typically

sensitive to (and may need to be repeated in response to) minor changes, for instance

different object conﬁgurations. The learned models are robust to such environmental

changes.

(a) (b) (c)

(d) (e) (f)

Fig.4. Sample images. (a)-(c) Original, (d)-(f) Segmented.

The segmentation performance (Figure 4) of the learned color map is similar with either

planning scheme. Over 20 images, the average segmentation accuracies of the learned

and hand-labeled color map are 94.9 ± 3.9 and 96.7 ± 4.3 respectively (no difference

at 95% signiﬁcance). Ground truth is provided by a human.

6 Conclusions

The potential of mobile robots can be exploited iff they operate autonomously. The

robot needs to be able to plan action sequences that facilitate the autonomous learning

(and adaptation) of models for environmental features. Two major challenges for robots

with color cameras are manual calibration and sensitivity to illumination changes. Prior

work has focused on modeling known illuminations [11], learning a few distinct col-

ors [3], and using heuristic models to plan action sequences that facilitate learning [4].

In this paper,we enable the robot to autonomouslylearn models for motion error and

learning feasibility. The long-term action-selection maximizes learning opportunities

while minimizing errors over the entire action sequence, resulting in better performance

than the greedy, heuristic approach that involves extensive manual parameter tuning.

Though we have presented results for color learning in a moderately structured scene,

similar techniques can be devised for other higher-dimensional features. In addition, the

planning scheme used to model colors can be applied to other learning/modeling tasks.

Both planning schemes require the environmental structure as input, which is much

easier to provide than hand-labeling several images. One challenge is to combine this

work with autonomous vision-based map building (SLAM) [20] so that structure can

also be largely learned by the robot. We also aim to combine the planned learning

approach with our prior work that detects and adapts to illumination changes [4]. The

ultimate goal is to develop algorithms for autonomous mobile robot operation under

natural conditions.

5151

References

1. Pineau, J., Montemerlo, M., Pollack, M., Roy, N., Thrun, S.: Towards Robotic Assistants in

Nursing Homes: Challenges and results. RAS Special Issue on Socially Interactive Robots

(2003)

2. Minten, B.W., Murphy, R.R., Hyams, J., Micire, M.: Low-order Complexity Vision-based

Docking. IEEE Transactions on Robotics and Automation 17 (2001) 922–930

3. Thrun, S.: Stanley: The Robot that Won the DARPA Grand Challenge. Journal of Field

Robotics 23 (2006) 661–692

4. Sridharan, M., Stone, P.: Color Learning on a Mobile Robot: Towards Full Autonomy under

Changing Illumination. In: The International Joint Conference on Artiﬁcial Intelligence.

(2007)

5. Brooks, R.A.: A Robust Layered Control System for a Mobile Robot. Robotics and Au-

tomation 2 (1986) 14–23

6. Boutillier, C., Dean, T., S.Hanks: Decision Theoretic Planning: Structural Assumptions and

Computational Leverage. Journal of AI Research 11 (1999) 1–94

7. Ghallab, M., Nau, D., Traverso, P.: Automated Planning: Theory and Practice. Morgan

Kaufmann, San Francisco, CA 94111 (2004)

8. Comaniciu, D., Meer, P.: Mean shift: A Robust Approach Toward Feature Space Analysis.

PAMI (2002)

9. Shi, J., Malik, J.: Normalized Cuts and Image Segmentation. In IEEE Transactions on PAMI

(2000)

10. Maloney, L.T., Wandell, B.A.: Color Constancy: A Method for Recovering Surface Spectral

Reﬂectance. Journal of Optical Soceity of America A 3 (1986) 29–33

11. Rosenberg, C., Hebert, M., Thrun, S.: Color Constancy using KL-divergence. In: The IEEE

International Conference on Computer Vision (ICCV). (2001)

12. Cohen, D., Ooi, Y.H., Vernaza, P., Lee, D.D.: UPenn TDP, RoboCup-2003: RoboCup Com-

petitions and Conferences. (2004)

13. Cameron, D., Barnes, N.: Knowledge-based Autonomous Dynamic Color Calibration. In:

The International RoboCup Symposium. (2003)

14. Jungel, M.: Using Layered Color Precision for a Self-calibrating Vision System. In: The

International RoboCup Symposium. (2004)

15. Schulz, D., Fox, D.: Bayesian Color Estimation for Adaptive Vision-based Robot Localiza-

tion. In: IROS. (2004)

16. Anzani, F., Bosisio, D., Matteucci, M., Sorrenti, D.: On-line Color Calibration in Non-

stationary Environments. In: RoboCup Symposium. (2005)

17. Four Legged: The RoboSoccer Four-Legged League (2007) http://www.tzi.de/

4legged/.

18. Bishop, C.M.: Neural Networks for Pattern Recognition. Oxford University Press (1995)

19. NN-Toolbox: Matlab Neural Network Toolbox (2007) http://www.mathworks.com/

access/helpdesk/help/toolbox/nnet/.

20. Jensfelt, P., Folkesson, J., Kragic, D., Christensen, H.I.: Exploiting distinguishable image

features in robotic mapping and localization. In: The European Robotics Symposium (EU-

ROS). (2006)

5252