ext-Dependent Speaker Identiﬁcation using

Spectrograms based on Conditional Quantization

Tridibesh Dutta

Indian Statistical Institute

203, B. T. Road, Kolkata - 700108, India

Abstract. The goal of this paper is to study a new approach to text dependent

speaker identiﬁcation using spectrograms. This, mainly, revolves around trapping

the complex patterns of variation in frequency and amplitude with time while an

individual utters a given word through spectrogram segmentation. These opti-

mally segmented spectrograms are used as a database to successfully identify

the unknown individual from his/her voice. The methodology used for identi-

fying, rely on classiﬁcation of spectrograms (of speech signals), based on tem-

plate matching of the conditionally quantized frequency-time domain features of

the database spectrogram samples and the unknown speech sample. Performance

of this novel approach on a sample collected from 40 speakers show that this

methodology can be effectively used to produce a desirable success rate.

1 Introduction

The process of automatically recognizing who is speaking by distinguishing qualities

in a speaker’s voice is called speaker recognition. For this purpose, it is important to

preserve the speaker speciﬁc information in the speech signal. Human voice has lots of

variations termed as intra-speaker variability. Variations in voice ‘in between’ speakers

is called inter-speaker variation. According to the relevance to the content of speech, the

speaker recognition task could be divided into ‘text independent’ and ‘text dependent’.

Moreover, the text-dependent speaker identiﬁcation can be subdivided into two

further categories, closed-set and open-set problems. The closed set text-dependent

speaker identiﬁcation problem may be stated as follows. Out of a total population of

N ‘known’ speakers, ﬁnd the speaker whose reference pattern has closest resemblance

to the sample pattern of the ‘unknown’ speaker who is assumed to be one of the given

set of speakers. In the open set problem, a reference model for an unknown speaker may

not exist. In this situation, an additional decision alternative, that the unknown does not

match any of the models, is required. This speaker veriﬁcation (in an open set) task is a

hypothesis testing problem where the system has to accept or reject a claimed identity

associated with an utterance. Since most of todays systems are based on probability cal-

culations, two types of erroneous decisions may occur in speaker veriﬁcation. A false

acceptance is said to occur when an impostor is accepted, while a false rejection occurs

when the system rejects a true client. There is a trade-off between these two error types.

If safety is emphasized, the false rejection rate will have to increase in order to keep the

false acceptance rate low. But if the system produces too many false rejections, users

Dutta T. (2008).

Text-Dependent Speaker Identiﬁcation using Spectrograms based on Conditional Quantization.

In Image Mining Theory and Applications, pages 133-142

DOI: 10.5220/0002338301330142

 SciTePress

may ﬁnd the system annoying. One common choice is to put the false acceptance and

false rejection rates equal, aiming for the equal-error-rate (EER) [1].

In this paper, text-dependent speaker identiﬁcation for both the closed set and open

set problems have been studied with. In the proposed method, speaker identiﬁcation

is carried out by means of speech spectrograms. Templates of stored spectrograms

are matched against the pattern to be recognized using similarity measures [2]. The

essence of this technique lies in formulating the speaker-identiﬁcation problem into

pattern recognition of images and resolving it using machine learning tools. This is a

notable drift from the usual the Vector Quantization (VQ) [3] and Gaussian Mixture

Models (GMM) [4] techniques for text-dependent speaker identiﬁcation.

Speaker Identiﬁcation task includes the basic components: (I) feature extraction (II)

speaker modeling (III) speaker matching and (IV) decision logic. The feature extraction

module converts the raw speech waveform in the given sample to a spectrogram. Dis-

tributional features of the spectrograms are then used to make representative codebooks

of speaker’s voice patterns and use them to create a database. Later, when unknown

samples arrive, they are used to match spectrograms from the given database. The deci-

sion logic ﬁnally makes a one-out-of-N decision, e.g. selects the speaker with maximum

degree of similarity.

A database designed for speaker identiﬁcation with limited enrollment data, is used

in the study. The database is collected in realistic conditions (normal room environ-

ment, which allowed room acoustics to interfere with the recordings) with the use of an

external microphone. The database contains 40 enrolled speakers, each reciting a list

of words. There are three words: ‘cat’, ‘gadget’ and ‘loss’; with each enrolled speaker

reciting each of the assigned words 6 times, of which 1 sample, for each word, are to be

randomly chosen for training purpose and the other 5 samples for testing. The speech

signals are sampled with 8 − 16kHz. Samples from every speaker are collected in dif-

ferent sessions varying over time, to make our database as efﬁcient as possible. Also,

before computation of the spectrogram, any DC offset present in the signals were re-

moved and the signals centered around 0 vertically, thus, denoising the speech signal

to an extent. The recorded samples were manually aligned by removing the initial and

trailing silence as much as possible. The maximum amplitude of the utterances was nor-

malized to −3dB, to ensure a fair comparison of the spectrograms. Frequencies with

intensity less than −70dB are screened.

The rest of this letter has been organized as follows: in Section 2, the spectrogram

feature extraction and modeling are explained. The identiﬁcation methods in closed and

in open set of speakers are described in Section 3. Experimental results are discussed in

Section 4. Applications and conclusion have been outlined in Section 5.

2 Spectrogram Processing

It can be seen from the spectrograms illustrated in Figures 1 and 2, the spectrograms

appear to be dissimilar for different speakers, for the utterance ‘gadget’. Hence, an es-

sential task of image comparison is to justify the claim. Spectrogram comparison to

recognize a speaker is already an established procedure in our text-dependent speaker

identiﬁcation problem [5, 7]. The spectrogram comparison approach for speaker iden-

134134

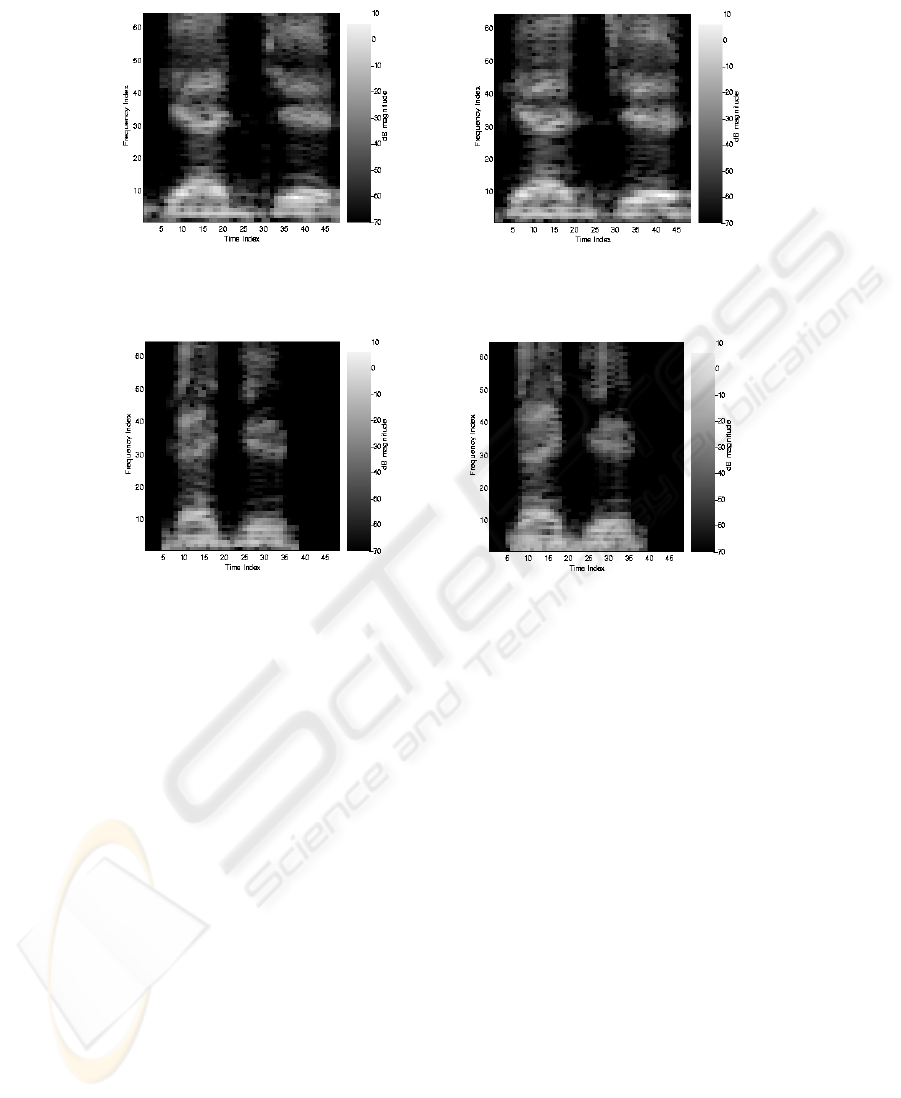
Fig. 1. Similarity in spectrograms for the utterance ‘gadget’ of the ‘Speaker 1’.

Fig. 2. Similarity in spectrograms for the utterance ‘gadget’ of the ‘Speaker 17’.

tiﬁcation proposed by Dutta and Basak [5], uses a non-parametric technique namely,

the Kolmogorov-Smironov test for image comparison comprising of Hollander-Wolfe

statistic [6]. In that, spectrograms are segmented along one axis and compared using the

cumulative distribution function of the gray-scale intensities taking into consideration

weights of different (frequency or time) bands. Segmenting along the frequency axis

resulted in lesser error rates than splitting the spectrogram along time axis. Optimality

in spectrogram segmentation was not treated [5].

In [7], the notion of a greedy search optimal spectrogram segmentation has been

introduced in which spectrograms were segmented into overlapping bands along the

frequency axis only, as in [5]. Then, spectrograms were compared by computing the

mean of each frequency band and taking into account the Euclidean distances between

corresponding bands of the spectrograms. This procedure adopted by Dutta [7], using

Euclidean distances (between the spectrograms of known and unknown speech sam-

ples) of the features of the frequency domain, does not capture information/features

from the overall time-frequency domains.

Under assumption that images are subject to random noise, we want to test if im-

ages are the same (the speech samples are of the same speaker). We say that two images

are the same if the corresponding bands of the segmented images have the same distri-

135135

butional properties. The choice of variable of interest to be extracted from the spectro-

grams is of utmost importance i.e. the variable which loses the least information about

the speakers. One may choose the statistical mean (ﬁrst moment), information entropy

(or Shannon entropy), the second central moment, the third and so on. It has been shown

in [7], that the the results are best when considering the mean of pixel values of bands

as the variable of interest.

The spectrograms are partitioned into several overlapping bands having near-ly

equal bandwidths and overlaps, for separate processing. Given a segmentation pattern,

all the spectrograms in question (each of which have the same pixel matrix size), are

split in a similar fashion. The number of bands a spectrogram is segmented into along

any axis, depends on the band-width and overlap. It is important to note here that, as the

number of bands differ, it is not always possible to segment a spectrogram into bands

having an ‘equal’ band-width and overlap. As a remedy, the spectrograms are split into

bands having a nearly equal bandwidths and overlaps. Though, the choice of the best

band-width and band-overlap selection remains to be an open problem, a good success

rate and speedy completion of the test may be assumed to satisfy an optimality crite-

rion. Results on effect of segmenting the spectrograms into bands along axes have been

provided in a later section. The motivation behind decomposition of the spectrograms

lie in a higher dimension comparison of the spectral features of two different images.

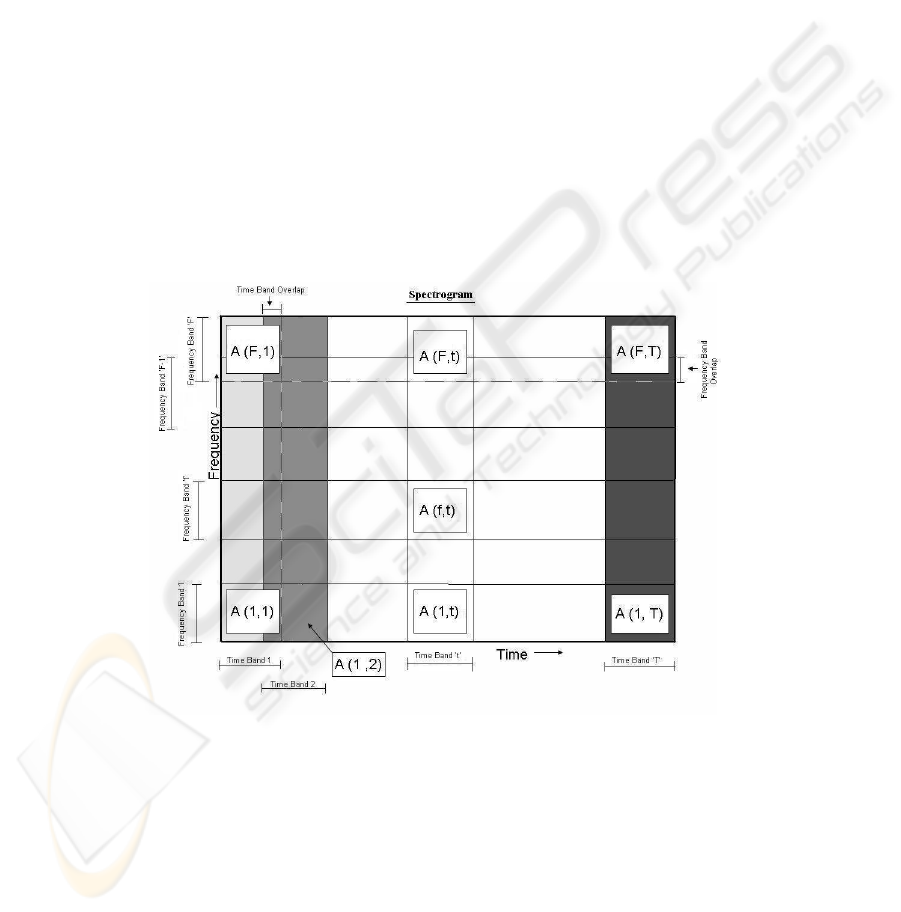
Fig. 3. Spectrogram segmentation into overlapping matrix cells.

The task of spectrogram segmentation has been formulated as follows: Split a spectro-

gram into an optimal number of overlapping bands along the frequency axis. Given this

segmented spectrogram, the entire image is again split into overlapping bands along the

time domain. The motivation behind this segmentation lies in the fact that it captures

information both along the time and frequency domain. A pictorial representation of

136136

the segmentation has been provided in Figure 3. The pixel values in these overlapping

ordered matrix cells A(f, t) (f = 1, 2, . . . , F ), (t = 1, 2, . . . , T ) may be interpreted

as the energy content in the cells (which uniquely characterizes an individual) as the

speech signal is swept through time. The matrix, A(f, t), is the intersection of pixel

cells of the f

frequency band and the t

time band.

As is depicted in the ﬁgure, the spectrogram has been segmented into several over-

lapping matrices. Let the mean of the pixel values of the (f, t)

matrix, A(f, t), be

given by µ

, where ‘f’ denotes the frequency band and ‘t’ denotes the time band.

Given a spectrogram of the speech signal of a speaker, the F -dimensional vector

(µ

, µ

, . . . , µ

F t

) (t = 1, 2, . . . , T ), represents the vocal properties of the speaker in

the t

time band.

In the database samples, let µ

ijrf t

denote the mean pixel values for replicate r cor-

responding to the (f, t)

matrix, A(f, t), of the spectrogram of the i

speaker’s utter-

ance of the j

word. Here, i = 1, . . . , N; j = 1, . . . , M ; r = 1, . . . , R; t = 1, . . . , T

and l = i, . . . , P . N denotes the number of speakers in the closed set; M, the number

of different words uttered; R, the number of replications per word used for training,

corresponding to each known speaker. F denotes the number of frequency bands the

spectrograms are segmented into in the frequency domain and T denotes the number of

time bands the spectrograms are split into along the time axis. We use these observa-

tions to prepare our codebook corresponding to each spectrogram. A typical codebook,

corresponding to the r

replicate of the j

word, of the i

speaker would consist of T

code vectors. The elements of each code vector would be representing the means of the

ordered overlapping matrices of the segmented (along frequency axis) time band and

the vector is given by Ψ

ijrt

= (µ

ijr1t

, µ

ijr2t

, . . . , µ

ijrF t

)

where t = 1, . . . , T . This

technique of data compression draws a close resemblance with quantization, in which

each time band is represented by a F -dimensional vector conditioning on the F fre-

quency bands. Quantization by conditioning on frequency bands enhances recognition

rate as it performs a superior template matching of images in question, than, uncon-

ditional vector quantization (of pixels in a particular time band) as in the later case,

the ordering/distribution of the centroids is not taken into consideration. Also, in vector

quantization, formation of empty clusters is likely, specially in time bands representing

silence or uniform energy content, thus, leading to erroneous results. This fact lays the

basis of our methodology to verify and, more importantly, identify a speaker.

3 Speaker Recognition

3.1 Identiﬁcation in a Closed Set

Having collected our training database of spectrograms for 40 speakers, 1 training sam-

ple for every word for every speaker is chosen randomly to be tested with. We consider

a test sample comprising of the 3 words of an unknown speaker (in the closed set).

An important assumption is that, the unknown speaker is in the closed set and utters

the three prescribed words in a predeﬁned order to enable identifying which sample

corresponds to which word.

Let θ represent the actual identity of the unknown speaker based on the mean pixel

values of the matrices of the segmented spectrogram. For simplicity, let the i

speaker

137137

in our database be denoted by ‘Speaker i’ (i = 1, . . . , 40). Given codebook C

ijr

rep-

resenting the i

speaker’s, r

replicate of the j

word, the minimizing value i of an

appropriately deﬁned ‘distance score’ [8–10] from the ‘unknown’ speaker’s codebook

, of the j

word, is a plausible solution to the speaker identiﬁcation problem, using

only the j

word. Mean pixel value of a particular matrix, A(f, t), of the segmented

spectrograms of a speciﬁc word by a speaker does not remain the same with replica-

tions due to variation in voice and also phase shifts. In the database samples, let the

vector deﬁned by Ψ

ijrt

= (µ

ijr1t

, µ

ijr2t

, . . . , µ

ijrF t

)

, be the centroid generated by

the t

time band of the r

replicate of the i

speaker’s utterance of the j

word.

Hence, C

ijr

= (Ψ

ijr1

, . . . , Ψ

ijrT

). Again, let x

θjf t

denote the mean of the unknown

speaker’s (f, t

)

matrix of the spectrogram corresponding to the j

word. Deﬁne the

codebook for the j

word of the unknown speaker as: S

= (s

, s

, . . . , s

), where

= (x

θj1t

, x

θj2t

, . . . , x

θjF t

)

, t

= 1, . . . , T .

Given an unknown speaker with identity θ, for the i

speaker and j

word, deﬁne

a ‘distance score’ D

θ|(i,j)

as:

min

r∈{1,...,R }

∈S

min

ijrt

∈C

ijr

d(s

, C

ijr

) (1)

where d(., .) is the distance metric deﬁned over the feature space [10, 11]. Typically,

Euclidean metric is used as the distance measure. The ‘distance score’ D

θ|(i,j)

proposed

in Eqn.(1) searches for the nearest neighbor (closest match) amongst all the replicates

of the i

speaker’s utterances of the j

word. This matching function:

∈S

min

ijrt

∈C

ijr

d(s

, C

ijr

)

is the quantization between two vector sets to be compared.

Utterances of different words serve as statistical blocking factors which enhances

recognition rate, experimental results of which has been presented in the ‘Results’ sec-

tion. Hence, incorporating the results from three words, classify, the unknown person θ

as the m

person if:

j=1

θ|(i,j)

(2)

achieves minimum for i = m, i.e. the ‘aggregate distance score’ [Eqn. (2)] between

the unknown speaker’s samples from the database samples of ‘Speaker m’ averaged

over 3 words is minimum.

Given this algorithm, results on choice of F , the ‘optimum’ number of frequency

bands; T , the ‘optimum’ number of time bands and R, the number of replicates required

for successful identiﬁcation has been depicted in a later section.

3.2 Identiﬁcation in an Open Set

In this case, the objective is slightly different and more difﬁcult. The problem is to

successfully identify a speaker who is in the set of 40 speakers and reject those who

138138

are not. Given a word, let two samples belong to the same cluster (i.e. the same speaker

as in our case), if the ‘distance score’ is less than some threshold distance d

[8]. It

is immediately obvious that the choice of d

is very important. Large values of d

will result in false acceptance. If d

is small, it’ll lead to false rejection. Hence, the

choice of the threshold ‘d

’ has to be such that it is greater than ‘average within speaker

distances’, but, less than the ‘between speaker distances’. Here, the modiﬁed codebook

for each replicate of the database speakers would contain the contents as in the closed

set case, as well as, the threshold distance value for the corresponding word of the

database speaker. A general framework to speaker recognition in an open set has been

presented in Figure 4.

Therefore, an ‘unknown’ speaker is said to be the m

speaker in the database if

and only if for each word his ‘distance score’ [Eqn. (1)] is less than the threshold value

for each word corresponding to the m

speaker. Experimental results have been

provided in the following section by randomly eliminating from the database, a set

of 5 speakers, and then choosing a speaker from the original 40 speakers to test for

identiﬁcation.

Fig. 4. Speaker recognition system in an ‘open set’.

4 Results

Successful identiﬁcation (in the text-constrained problem) in a closed set of speakers by

choosing the vector-valued statistical mean of the pixel values of each time band as the

variable of interest and an appropriate choice of R (the number of replicates for each

word required for training) has been depicted in Table 1. The pixel matrix size of each

spectrogram is 253 × 271. Optimal values of F and T were computed to be 10 and 9,

respectively, for this algorithm, with average optimal bandwidth 46 and band-overlap

23 along the frequency axis. The average optimal bandwidth along the time axis is 38

and band-overlap 10. Corresponding results, for successful identiﬁcation, when using

imaging procedures proposed in [5] and [7], has also been summarized in Table 1.

A comparative study of ‘success rates’ when identifying speaker by Hollander-

Wolfe Statistic [5] and Euclidean distances [7], which are, based on frequency domain

139139

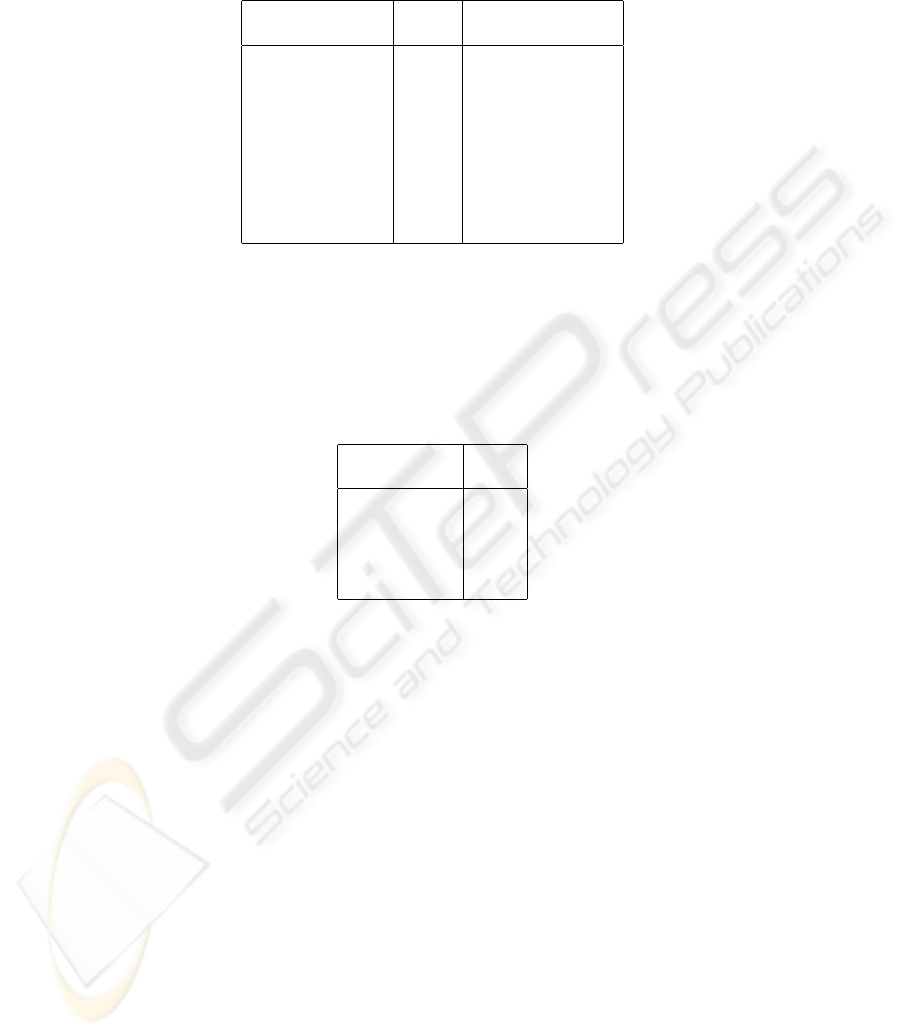
Table 1. Results based on 100% successful identiﬁcation in closed set identiﬁcation. (R: Training

replicates used for each word, for each speaker.).

Methodology Value of CPU run-time

used R to identify a speaker

Proposed ‘aggregate 1 0.57 sec.

distance score’

Euclidean 4 0.98 sec.

distance [7]

Hollander-Wolfe 3 1.4 sec.

Statistic [5]

only has been presented in Table 2. As is evident from the Tables 1 and 2, the efﬁciency

registered (taking one replicate for each of the three words), to successfully identify a

speaker is higher in the proposed algorithm than the benchmark techniques suggested

in [5] and [7].

Table 2. Success Rates when using other techniques for R. = 1, in closed set identiﬁcation.

Technique Success

used Rate

Euclidean 85%

Distance [7]

Hollander-Wolfe 67%

Statistic [5]

Though, successful identiﬁcation of a speaker from just a word, by calculating the min-

imum ‘distance score’ (based on 1 training sample), may be as low as 65 − 80%; com-

bining results from the 3 words, computing the ‘aggregate distance score’ (as stated in

Speaker Identiﬁcation) and choosing an appropiate database size for every speaker (1

speech sample for each of the three words for each speaker as in the case study), one

can obtain as good as 100% success rate in identiﬁcation in a closed set text-constrained

problem. Results are as stated in Table 1. While, identiﬁcation rate when the spectro-

gram is not segmented is as low as 27.5% (when using mean of the pixel values of

the entire spectrogram), segmenting the spectrogram along both axes and working with

the mean values of the ordered overlapping matrices yielded better results which is

as shown in Figure 5. In [7], when segmenting only along the frequency axis, it was

shown that for the given dataset, the best results were achieved when segmenting the

spectrograms into 10 overlapping bands. Figure 5 plots the results, for segmenting the

spectrogram into a varying number of overlapping time bands, given that the spectro-

gram has been already been segmented into 10 bands along the frequency axis.

Conducting 200 tests (each test comprising of 3 test spectrograms corresponding

to the three words uttered by a speaker amongst the closed set of speakers) for each

140140

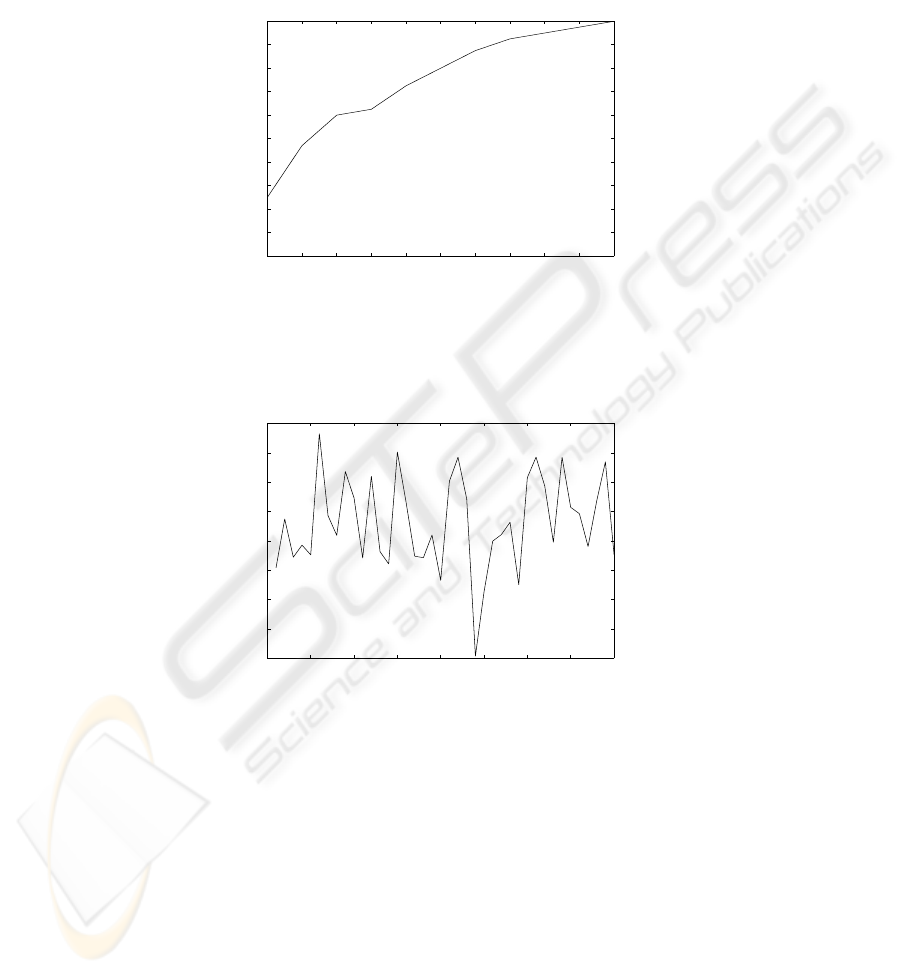
mentioned procedure, Success Rates, when it is known that the unknown speaker is

from the closed set, have been computed which is as shown in Table 1. Figure 6 gives

a plot of the comparative (proposed) aggregate distance score an ‘unknown speaker’

(Speaker ID:24) has with the database samples of the speakers 1, . . . , 40.

1 2 3 4 5 6 7 8 9 10 11

100

Number of time bands −>

Success percentage in speaker identification −>

Fig. 5. Success Rates on segmenting the spectrogram along time axis (given that the spectro-

gram has already been split into 10 overlapping bands in the frequency domain) when comparing

‘unknown speakers’ (closed set) with the known database.

0 5 10 15 20 25 30 35 40

1200

1400

1600

1800

2000

2200

2400

2600

2800

Speaker ID −>

Aggregate Distance Score −>

Fig. 6. Aggregate Distance Score Vs. Speaker when comparing an ‘unknown speaker’ (Speaker

ID:24) with the known database samples.

In the open set classiﬁcation, given a word, using the average ‘within speaker distance’

, as the threshold value, for each word (corresponding to every speaker), the false

rejection or false acceptance rates in identiﬁcation when a ‘unknown’ speaker may or

may not be in the closed set of speakers, was determined. This method of computa-

tion of d

satisﬁed the equal-error-rate criterion (EER) [1] (stated in the ‘Introduction’

section), which was computed to be 0.136. On increasing the value of d

, as expected,

the rate of false acceptance increases, while the value of false rejection falls, which is

certainly not desirable.

141141

5 Applications and Conclusions

This paper presents a method for successful text-dependent speaker identiﬁcation based

on extracting unique speaker effects on the pronunciation of a word. In view of the

results presented here, the proposed technique outperforms the spectrogram comparison

methodologies adopted before.

This methodology can be used to identify speakers in password protected zones

where a database of voices of speakers can be used as passwords. This model, if re-

quired, can be made more dynamic by adding the ‘most recent successful voice accep-

tance’ of a particular speaker into his/her database of samples, discarding his/her spec-

trogram corresponding to earliest voice sample in the database. This dynamic model,

takes into consideration the change in voice of a particular speaker over time.

Future work will focus on more robust nearest neighbor classiﬁers, better selection

of words, optimality of bandwidth selection, implementation of this technique on a

large-scale and in text-independent case. Also, it would be important subsequently, to

reduce its computational complexity and computation time even further.

References

1. Olsson J.: Text Dependent Speaker Veriﬁcation with a Hybrid HMM/ANN System. Thesis

Project, downloadable at http://www.speech.kth.se/prod/publications/ﬁles/1630.pdf.

2. Jain Anik K., Duin Robert P. W. and Jianchang M.: Statistical Pattern Recognition: A Review.

IEEE Transactions on Pattern Analysis and Machine Intelligence, Volume 22, Issue 1(January

2000), pp. 4-37, 2000.

3. Soong F.K., Rosenberg A.E., Juang B.H. and Rabiner L.R.: A vector quantization approach to

speaker recognition. AT & T Technical Journal, 66:14-26, pp. 1987.

4. Reynolds D. A.: Speaker identiﬁcation and veriﬁcation using Gaussian mixture speaker mod-

els. Speech Commun. 17 (1995), pp. 91-108.

5. Dutta T. and Krishna Basak G.: Text dependent speaker identiﬁcation using similar patterns

in spectrograms. PRIP’2007 Proceedings, Volume 1, pp. 87-92, Minsk, 2007.

6. Demidenko E.: Kolmogorov-Smirnov image comparison. Lecture Notes Comp Sci 3056: 933-

938, 2004.

7. Dutta T.: Text dependent speaker identiﬁcation based on spectrograms. Accepted paper in The

Twenty Second International Image and Vision Computing New Zealand (IVNCZ 2007) to be

held at Hamilton, New Zealand, December 5-7, 2007.

8. Duda R. O., Hart P. E. and Stork D. G.: Pattern Classiﬁcation. John Wiley and Sons, 2006.

9. Hastie T., Tibshirani R. and Friedman J.: The Elements of Statistical Learning: Data Mining,

Inference and Prediction. Springer, 2001.

10. Webb R. A.: Statistical Pattern Recognition. John Wiley and Sons, 2002.

11. Gupta H., Hautamki V., Kinnunen T. and Frnti P.: Field Evaluation of Text-

Dependent Speaker Recognition in an Access Control Application. Paper, downloadable at

http://cs.joensuu.ﬁ/pages/pums/public results/DTWpaper.pdf.

142142