Fast Multi-View Evaluation of Data
Represented by Symmetric Clusters
Alexander Vinogradov
A. A. Dorodnicyn Computing Centre, Russian Academy of Sciences
Vavilov str. 40, 119333 Moscow, Russian Federation
Abstract. A new framework is proposed for a fast calculation of linear scalings
posed on structured data. Several widely used types of data representation based
on clusters with intrinsic features of local simmetry are taken into account. Pa-
per presents some Image Mining technologies that are used for improvement of
abstract data multi-view evaluation procedures.
1 Introduction
On-line estimation of standard parameters concerning to big samples is usually per-
formed on the basis of preliminary calculation and accumulation of frequently used
intermediate values. The greater the costs of time expenditures, the more numerous in-
termediate data become. A characteristic example is given by systems of class OLAP
(On-Line Analytical Processing) in which files of aggregates prepared in advance can
surpass in size initial sample in tens and hundreds times [5], [12]. Nevertheless, mul-
tiple view is quite necessary for many types of data, in particular, for various types of
spatially distributed data, 3D scenes and images. Recently hypercubes and other ad-
vanced architectures and methods quickly spread and benefit in many applications of
Image Processing and Image Mining technologies, for instance, in GIS [9], [10], [11].
And, vice-versa, some technologies of IP and IM turn out to be useful in processing
abstract samples in structured data spaces [4], [7]. A subject matter of the paper be-
longs to this last class of methods: we develop a framework providing fast evaluation
of density distributions for arbitrary linear scalings posed on a data sample. Techniques
described here use certain properties of spatial symmetry that are specific to clusters of
some widely used types of data representation.
1.1 Multiple View on a Data Sample
Existing software products and systems of the specified type are focused, mainly, on
calculation of several key parameters of data. At the same time, inquiries of refined
analysts concern often also to various non-standard relations of parameters for each of
which aggregated scales can’t be prepared in advance [2], [4], [6]. Such inquiries can
concern to spatiotemporal relations, indirect or hidden indicators, actual and presup-
posed dependencies, and so on [1], [3], [8]. In some cases that we address to in what
Vinogradov A. (2008).
Fast Multi-View Evaluation of Data Represented by Symmetric Clusters.
In Image Mining Theory and Applications, pages 53-57
DOI: 10.5220/0002338600530057
Copyright
c
 SciTePress

follows, it is possible to perform fast estimations of corresponding distributions with-
out direct use of bulky files of data. By the equation of arbitrary relation A(x) = a
an a-parametric scaling is determined in the data space X. Projections of clusters of
X onto the parameterization scale automatically form sampling estimates of the den-
sity distribution for a. If the form of clusters possesses properties of isotropy, i.e., to
some extent it is invariant with respect to linear transformations belonging to the group
SO
N
, in some cases it is possible to replace all procedures of calculation and gathering
projections by simple summation of values that are independent on actual direction of
a-layers in X.
2 Local Linear Transforms
We assume that for a sample X = {x
i
} ⊆ R
N
, i ∈ I, of great volume |I|, some kind
of preliminary segmentation or structuring was made that can be permanently refined
with new data. The situation is widespread when such pre-segmentation produces an
estimation of empirical density f
I
(x) =
1
|I|
P
R
δ(x −x
i
)dx in the form of finite sum
g(x) =
P
λ
k
g
k
(x), in which every component g
k
(x) represents in the vicinity of its
center x
k
a limited function h of some positively determined 2-form B
k
of coordinates:
g
k
(x) = h((x − x
k
)
T
B
k
(x − x
k
)), where λ
k
are aprioristic weights. Examples are:
normal mixtures, final sets of ellipsoidal clusters, of ”thick” spheres, etc. The last type
of vicinities is specific to data of the highest dimension, first of all, for long time series
(for example, the sphere with ”thickness” 0.01R contains more than 90% of the volume
of 1000-dimensional sphere).
2.1 Advantages of Clusters with Symmetry
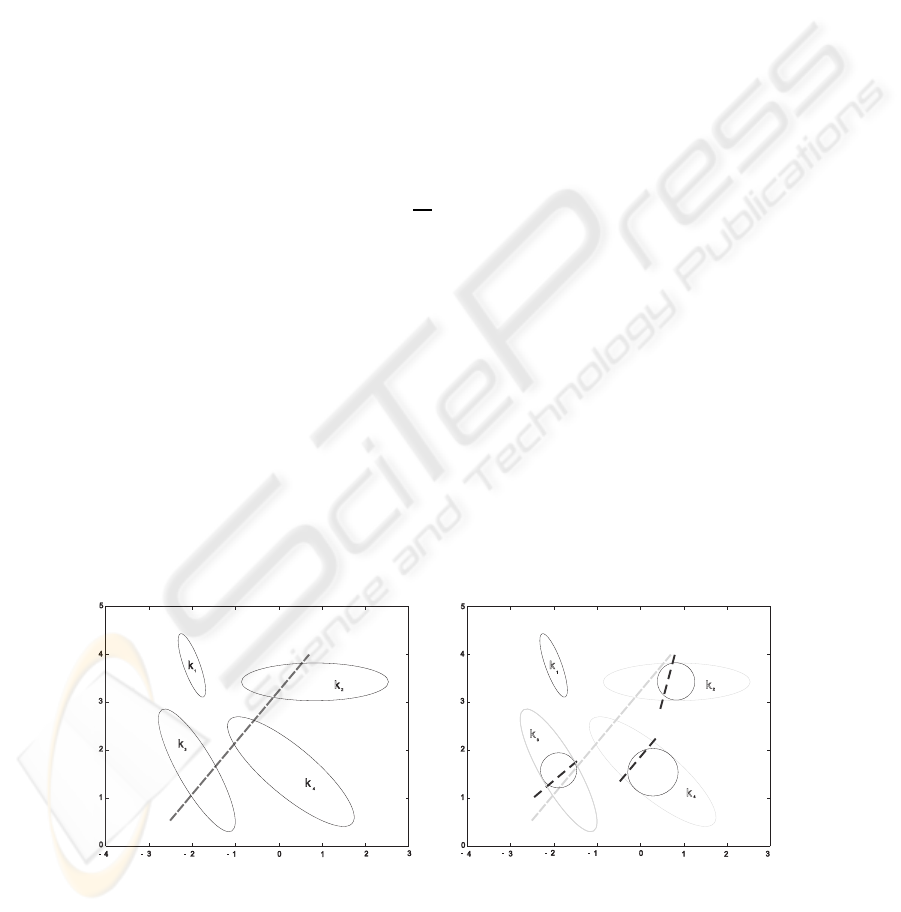
The common for these representations (see Fig. 1) is that in the vicinity of the center x
k
each component of the sum
P
λ
k
g
k
(x) is resulted by some invertible linear transform
L
k
to spherically symmetric form g
sk
(y
k
) = h
s
(
P
(y
k
n
)
2
),
R
g
sk
(y
k
)dy
k
= 1.
Fig.1. Clusters of initial representation are rebuilt to isotropic ones via local transforms. Linear
layer of a scaling (dotted line, left) is replaced with its transformed images (right).
5454

If the integral
R
L
k
(S
a
)
g
sk
(y
k
)dy
k
on the image L
k
(S
a
) of a layer S
a
is easily calculable
(or can be represented by table values prepared in advance along with permanent refine-
ment of the representation
P
λ
k
g
k
(x)), an estimation of aprioristic distribution of scal-
ing parameter p(a) =
P
µ
k
(c
k
)
R
g
sk
(y
k
)dy
k
is reduced to an arrangement of trans-
formed layers L
k
(S
a
) in R
N
, and also to calculation of factors µ
k
(c
k
), adhering coordi-
nates y
k
to uniform scale of scalar parameter a. In a linear case, when A(x) =
P
c
j
x
j
,
all layers are hyper-planes of dimension N − 1, and the value
R
L
k
(S
a
)
g
sk
(y
k
)dy
k
de-
pends only on the distance from component’s center x
k
to the image L
k
(S
a
) of a layer
S
a
whatever direction of vector c
k
j
, j ∈ {1, ..., N }, taken in the space R
N
.
3 Fast Calculations on Isotropic Clusters
The form of each linear transform L
k
is uniquely (and simply) determined by the equa-
tion A(x) =
P
c
j
x
j
and by the main axes of the initial shape of cluster k. Let matrixes
of these transforms are constructed for all components. In a linear case factors µ
k
(c
k
)
are determined by the formula
µ
k
(c
k
) =
PP
(c
k
j
(L
k
)
−1
ij
)
2
P
(c
k
j
)
2
!
1
2
(1)
If we exclude from the analysis exotic types of distributions g
k
(x) used in integrals on
transformed layers L
k
(S
a
), then obvious formulas can be written out. We show here as
examples the two corresponding estimates of density p(a) for cases of a normal mixture
and a set of uniformly filled ellipsoids.
For a normal mixture:
p(a) =
1
√
2π
X
λ
k
µ
k
(c
k
)exp −
1
2
(a −
P
c
k
j
x
k
j
)
2
PP
(c
k
j
(L
k
)
−1
ij
)
2
!
(2)
For a set of ellipsoids:
p(a) =
1
√
π
Γ (
N
2
+ 1)
Γ (
N−1
2
+ 1)
X
λ
k
µ
k
(c
k
) 1 −
(a −
P
c
k
j
x
k
j
)
2
PP
(c
k
j
(L
k
)
−1
ij
)
2
!
N −1
2
(3)
So, if a data representation of specified type is used, then for evaluation of distributions
on linear scales A(x) =
P
c
j
x
j
it is enough to make weighted by factors (1) transver-
sal summations on always the same set of k one-dimensional files of size n
k
filled
with predefined constants
R
L
k
(S
a
)
g
sk
(y
k
)dy
k
, where n
k
depends only on a necessary
detailing of the density p(a).
3.1 Possible Generalizations
Certainly, mixed combinations are admissible, when the sum
P
λ
k
g
k
(x) contains com-
ponents g
k
(x) of different types. In general case a critical point is a choice of suitable
5555

piece-wise approximationof the scaling A(x) = a. For a single linear scaling each clus-
ter intersects with entire (N −1)-hyper-plane, but the calculation of its partial crossings
with linear pieces proves to be a separate hard analytical and computational problem
even for simple equations of kind A(x) = a, especially when N grows. Approximate,
but yet computationally efficient solutions can be found in cases when actual repre-
sentations
P
λ
k
g
k
(x) consist of numerous compact clusters that are small enough to
embody close to exactly plain fragments of a smooth non-linear a-layer (see Fig. 2).
This condition can be directly satisfied for diminishing ellipsoids in sparse clusterings,
Fig.2. Plain piece-wise approximation of intersections of smaller clusters with layers of a smooth
non-linear scaling A(x) = a.
but for kernels with infinite support (such as Gaussian ones) some additional assump-
tions are necessary, for instance, usage of kernels cut within ellipsoids that contain main
share of kernels’ volume. In any case, computation of values of type (2), (3) is a prob-
lem essentially less complicated, than pre-calculation and warehousing of numerous
data aggregations or a direct calculation on the sample X = {x
i
}.
4 Conclusions
A framework was proposed for efficient estimation of a distribution taking place on
parameter a scale of arbitrary linear scaling A(x) = a posed on a big data sample. It
was shown that in special cases it is possible to replace all procedures of calculation
of a sample share represented in any global a-layer by simple weighted summation of
highly limited number of predefined values. Besides exactly computational advantages,
basic improvements of estimates p(a) are provided on this way in the case when it’s
ensured a priori, that not only approximation, but also the true distribution of the sample
5656

X = {x
i
} is a mixture of the form
P
λ
k
g
k
(x). Then formulas of type (2) or (3)
containing estimates of parameters x
k
, c
k
, B
k
, µ
k
obtained on the basis of searching all
the set of initial data, will be more exact, than nonparametric density estimates provided
by restricted fragments situated in layers of scaling A(x) = a, in particular,more exact,
than similar evaluations produced from standard aggregates or other partial histograms.
The framework could be useful in applied tasks concerning to mining and analytical
processing images and other big data sets represented by clusters with described above
features of symmetry.
Acknowledgements
This work was supported by the Russian Foundation for Basic Research (05-01-00332,
05-07-90333,06-01-00492, 06-01-08045, 07-01-12020), and the Grant of Presidium of
RAS ”Scientific Schools” No 5833.2006.1.
References
1. Alejandro A. Vaisman, Alberto O. Mendelzon, Walter Ruaro and Sergio G. Cymerman: Sup-
porting dimension updates in an OLAP server. Information Systems, Volume 29, Issue 2
(2004) 165-185
2. Alfredo Cuzzocrea: Improving range-sum query evaluation on data cubes via polynomial
approximation. Data & Knowledge Engineering, Volume 56, Issue 2 (2006) 85-121
3. Chun-Che Huang, Tzu-Liang (Bill) Tseng, Ming-Zhong Li and Roger R. Gung: Models
of multi-dimensional analysis for qualitative data and its application. European Journal of
Operational Research, Volume 174, Issue 2 (2006) 983-1008
4. Damianos Chatziantoniou: Using grouping variables to express complex decision support
queries. Data & Knowledge Engineering, Volume 61, Issue 1 (2007) 114-136
5. J. Mundy: Smarter data warehouses. Intelligent Entherprise v.4 No 3 (2001) 100-120
6. Ki Yong Lee, Jin Hyun Son and Myoung Ho Kim: Reducing the cost of accessing relations
in incremental view maintenance. Decision Support Systems, Volume 43, Issue 2 (2007)
512-526
7. Ming-Chuan Hung, Man-Lin Huang, Don-Lin Yang and Nien-Lin Hsueh: Efficient ap-
proaches for materialized views selection in a data warehouse. Information Sciences, Volume
177, Issue 6 (2007) 1333-1348
8. Navin Kumar, Aryya Gangopadhyay and George Karabatis: Supporting mobile decision
making with association rules and multi-layered caching. Decision Support Systems, Vol-
ume 43, Issue 1 (2007) 16-30
9. Owen Kaser and Daniel Lemire: Attribute value reordering for efficient hybrid OLAP. Infor-
mation Sciences, Volume 176, Issue 16 (2006) 2304-2336
10. Pierre Marchand, Alexandre Brisebois, Yvan Bedard and Geoffrey Edwards: Implementation
and evaluation of a hypercube-based method for spatiotemporal exploration and analysis.
ISPRS Journal of Photogrammetry and Remote Sensing, Volume 59, Issues 1-2 (2004) 6-20
11. Sonia Rivest, Yvan Bedard, Marie-Jose Proulx, Martin Nadeau, Frederic Hubert and Julien
Pastor: SOLAP technology: Merging business intelligence with geospatial technology for
interactive spatio-temporal exploration and analysis of data. ISPRS Journal of Photogram-
metry and Remote Sensing, Volume 60, Issue 1 (2005) 17-33
12. Young-Koo Lee, Kyu-Young Whang, Yang-Sae Moon and Il-Yeol Song: An aggregation
algorithm using a multidimensional file in multidimensional OLAP. Information Sciences,
Volume 152 (2003) 121-138
5757