Can Feature Information Interaction Help for

Information Fusion in Multimedia Problems?

Jana Kludas

, Eric Bruno

and Stephane Marchand-Maillet

University of Geneva, Switzerland

Abstract. The article presents the information-theoretic based feature informa-

tion interaction, a measure that can describe complex feature dependencies in

multivariate settings. According to the theoretical development, feature interac-

tions are more accurate than current, bivariate dependence measures due to their

stable and unambiguous deﬁnition. In experiments with artiﬁcial and real data

we compare the empirical estimates of correlation, mutual information and 3-

way feature interaction. We can conclude that feature interactions give a more

detailed and accurate description of data structures that should be exploited for

information fusion in multimedia problems.

1 Introduction

With the rise of the Web 2.0 and its tendencyto populate the WWW more and more with

images and videos multimedia related topics became lively discussed ﬁelds of research.

In its core there is an essential need for information fusion due to the multi modal na-

ture of multimedia data. Hence the fusion of multi modal data (e.g. text and images)

has a large impact on algorithms like multimedia indexing, retrieval and classiﬁcation,

object recognition as well as for data preprocessing like feature selection or data model

development. Information fusion has established itself as an independent research area

over the last decades, but a general theoretic framework to describe general information

fusion systems is still missing [6]. Up to today the understanding of how fusion works

and by what it is inﬂuenced is limited. Probably that is one reason why in multimedia

document retrieval for web applications the visual component is up to today lacking

behind expectations as can be seen for example in the INEX 2006 [24] and 2007 Multi-

media Track , where text-only based runs outperformed all others. As another example

can be named the text-based image searches from Google, Yahoo! and others.

All work done so far on information fusion in multimedia settings can be divided

into two main directions: (1) fusion of independent or complementary information by

assuming or creating independence and (2) fusion of dependent information by exploit-

ing their statistical dependencies. Both approaches have been applied in multimedia

processing problems equally successfully - for some tasks the fusion on independent

sources outperforms the algorithms based on dependent sources, on other tasks it is the

other way around. Neither of these approaches is in general superior.

Aligned to the second approach we like to investigate another way of analyzing

input data for multimedia problems based on feature information interactions with the

Kludas J., Bruno E. and Marchand-Maillet S. (2008).

Can Feature Information Interaction Help for Information Fusion in Multimedia Problems?.

In Metadata Mining for Image Understanding, pages 23-33

DOI: 10.5220/0002339500230033

 SciTePress

long term goal of information fusion performance improvement. This multivariate, in-

formation theoretic based dependence measure is more accurate in ﬁnding the data’s

structure e.g. situations, where the independence assumption is sufﬁcient and where the

dependency between the input data is not negligible.

Information interaction is superior to traditional dependence measures due to its

consistent deﬁnition, its global application to the whole feature set and its capture of

linear and higher order statistical dependencies. Considering this new deﬁnition of fea-

ture interactions current machine learning algorithms do not treat the feature’s statisti-

cal dependencies properly. Hence the investigation of feature interactions in multimedia

data could help to improve the information fusion and hence the whole performance of

the entailed retrieval and classiﬁcation algorithm.

In Section 2 we discuss in more detail state-of-the-art fusion approaches with in-

dependent and dependent input data and their shortcomings. Thereafter we present in

Section 3 the idea of feature interaction information and how it can help to improve

information fusion algorithms. In Section 4 we give the results of data analysis exper-

iments with artiﬁcial and real data, which is followed by the conclusions in Section

2 Related Work

Our article discuss the problem of information fusion, but most of the related work can

be found in multimedia processing where information fusion is only implicitly treated

as one part of the problem. We review some example approaches and explain when and

why they can fail.

In early years of information fusion research scientists fused different sources by

assuming independence between them as in one of the ﬁrst works on classiﬁer and

decision fusion on fusing neural network outputs [4]. The independence assumption is

still widely used in machine learning as e.g. in the naive Bayes classiﬁer. Its success is

based on its simplicity in calculation and the learned models, as well as its robustness

in estimating the evidence [18]. Approaches that fuse independent or complementary

sources mostly belong to classiﬁer and decision fusion, where ﬁrst each modality of

the input is treated separately and then a ﬁnal decision is based on the single results.

Applications that can be found in literature are for example multimedia retrieval [14,

12], multi modal object recognition [5], multi-biometrics [7] and video retrieval [15].

Despite its successful application for some problems it seems to fail completely for

others. In [7] it is shown that the violation of the independence assumption hurts the in-

formation fusion performance. So a trade off between simple and fast calculated results

and their accuracy is necessary. That loss in performance was empirically undermined

in [9], where they showed that the maximum performance improvement in a multi-

biometrics application can be only achieved, if the statistical dependencies between the

modalities are taken into account. Independence assumption based algorithms are also

called myopic, because they treat all attributes as conditionally independent given the

class label [25].

To circumvent the problem of attribute dependencies in data other approaches try

to create independence with the help of linear transformation methods like principal

2424

and independent component analysis (PCA/ICA), factor analysis and projection pur-

suit as reviewed in [19]. Unfortunately these methods are not sufﬁcient to eliminate

all dependencies in the data, since they target only pairwise and linear feature depen-

dencies [20]. In addition the authors showed empirically that their multi modal object

recognition problem is affected by higher order dependency patterns. A similar result

was found in [16]. In the multimedia classiﬁcation task the Support Vector Machine

(SVM) approach using an ICA-based feature selection was outperformed by a SVM

on the original data set. Multimedia processing approaches that exploit explicitly at-

tribute dependencies fuse the information preferably at data or feature level. Example

applications are multimedia summarization [1], text and image categorization [3], multi

modal image retrieval [13] and web document retrieval [8]. Those approaches exploit

all some form of attribute dependency at data level like co-occurrence (LSI [28]), corre-

lation (kCCA [16]) or mutual information. As examples for late fusion, where classiﬁer

dependencies are exploited, can be named copula functions [27] or nonlinear fusion

algorithms based on SVM’s [2].

The most important shortcoming of those algorithms is that they only take bivariate

dependencies into account, even though they work in a multivariate setting [21]. High

level feature relationships such as conditional dependencies of a feature pair to a third

variable e.g. the class label are neglected. For now there exists no prove that this higher

order dependencies have an impact on the performance of multimedia processing sys-

tems, but in [22] their exploitation led to a performance improvement.

3 Feature Information Interaction

Before the introduction of feature interaction by [17,18] there was no unifying deﬁni-

tion of feature dependence in multivariate settings, but similar formulae have emerged

independently in other ﬁelds from physics to psychology. Feature information interac-

tion or co-information as it was named in [23] is based on McGill’s multivariate gen-

eralization of Shannon’s mutual information. It describes the information that is shared

by all of k random variables, without overcounting redundant information in attribute

subsets. So it ﬁnds irreducible and unexpected patterns in data that are necessary to

learn from data [26].

This general view of attributeinteractions could help machine learning algorithms to

improve their performance. For example attribute interactions can be helpful in domains

where the lack of expert knowledge hinders the selection of very informative attributes

sets by ﬁnding interacting attributes needed for learning. Another example is the case

when the attribute representation is primitive and attribute relationships are more im-

portant than the attributes themselves. Then similarity based learning algorithms will

fail, because the proximity in the instance space is not related to classiﬁcation in this

domain.

Two levels of interactions can be differentiated: (1) relevant non-linearities between

the input attributes, which are useful in unsupervised learning and (2) interactions be-

tween the input attributes and the indicators or class labels, which is needed in super-

vised learning. The k-way interaction information as found in [17] for a subset S

⊆ X

of all attributes X = {X

, X

, ..., X

} is deﬁned as:

2525

I(S) = −

T ⊆S

(−1)

|S|−| T |

H(T ) = I(S \ X|X) − I(S \ X), X ∈ S (1)

with the entropy deﬁned as:

H(S) = −

¯υ∈

P (¯υ)log

P (¯υ), (2)

where the cartesian product of the sets of attribute values

X = X

× X

× ... × X

is used. The feature interaction for k = 1 reduces to the single entropy, for k = 2 to the

well known mutual information and for k = 3 attributes to McGill’s multiple mutual

information:

I(A; B) = H(A) + H(B) − H(A, B) (3)

I(A; B; C) = I(A; B|C) − I(A; B) (4)

= H(A, B) + H(A, C) + H(B, C) (5)

− H(A) − H(B) − H(C) − H(A, B, C). (6)

According to this deﬁnition 3-way information interaction will be only zero iff A

and B are conditionally independent in the context of C, because then I(A; B|C) =

I(A; B). So it gives only the information exclusively shared by the involved attributes.

Information interactions are stable and unambiguous, since adding new attributes is not

changing already existing interactions, but only adding new ones. Furthermore they are

symmetric and undirected between attribute sets.

It is not to be confused with multi-information as presented in [21]. This dependence

measure is based on the Kullback-Leibler divergence between the joint probability of

, i = 1...M attributes and their marginals:

multi

(X) =

H(X

) − H(X) =

P (x)log

P (x)

P (x

)

(7)

Multi information results for i = 2 as well in mutual information, but for i = 3

attributes it differs from the information interaction:

multi

(A, B, C) = H(A) + H(B) + H(C) − H(A, B, C). (8)

Hence it can capture higher order statistical dependencies, but is not taking the pair-

wise interactions into account. This way multi-information overﬁts the k-way mutual

information by counting redundant feature dependencies several times.

Another interesting point about feature information interaction is that it results in pos-

itive and negative values, which represent two different types of feature interactions.

An explanation using synergy and redundancy between attributes that was given in [17,

18], is presented in the following.

2626

3.1 Positive Interaction: Synergy

In case of positive interactions the process beneﬁts from an unexpected synergy in the

data. In statistics this phenomena is called moderating effect and is known a long time.

Synergy occurs when A and B are statistical independent, but get dependent in the

context of C as can be seen in Figure 1(a). In [17] this type of interaction is described

as observational, because the relationships between the features can only be found by

looking at all of them at once. Myopic feature selections are unable to exploit the syn-

ergy in the data. It can be exploited e.g. for feature selection in supervised learning or

for feature construction in the unsupervised case.

(a) synergy (b) redundancy

Fig.1. Interaction diagrams of different types of information interactions between A, B and C.

3.2 Negative Interaction: Redundancy

Negative interactions occur when attributes partly contribute redundant information in

the context of another attribute, which leads to a reduction of the overall dependence.

It is shown in Figure 1(b) on behalf of the redundant attributes A, B towards a third

attribute C. This type of interaction is also called representational, because it includes

some conditions on all involved attributes. In supervised learning the negative inﬂu-

ence of redundancy can be resolved by eliminating unneeded redundant attributes, but

it could be advantageous in unsupervised learning in the case of noisy data.

In any case myopic voting function that are based on the independence assumption

as well as fusion algorithms that use only local dependencies are confused by positive

and negative feature interactions, which results in decreased information fusion perfor-

mance. In general it is harder to resolve the inﬂuence of negative interactions.

In the following section we compare empirical estimates of correlation, mutual in-

formation and 3-way feature information interaction for artiﬁcial and real multi modal

data to draw conclusions about their usefulness as dependence measure in information

fusion.

4 Experiments

For the objective evaluation of the different dependence measures we ﬁrst conducted

tests on simple artiﬁcial data sets, where the relations between the input variables as

well as their relations towards the class labels are known.

2727

features

1 2 3 4 5 6 7 8 9

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.05

0.1

0.15

0.2

0.25

p(x)

(a) absolute correlation, zero-bar: 0%

classes

features

0.5 1 1.5 2 2.5 3 3.5

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

p(x)

(b) absolute correlation, zero-bar: 0%

features

1 2 3 4 5 6 7 8 9

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

p(x)

classes

features

0.5 1 1.5 2 2.5 3 3.5

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

p(x)

(d) mutual information, zero-bar:68%

features

1 2 3 4 5 6 7 8 9

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

p(x)

(e) 3-way interaction (f v

= 1) zero: 69%

features

1 2 3 4 5 6 7 8 9

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

p(x)

(f) 3-way interaction (cl = 1) zero: 60%

Fig.2. Unsupervised (a,c,e) / supervised (b,d,f) case for AND combined artiﬁcial data.

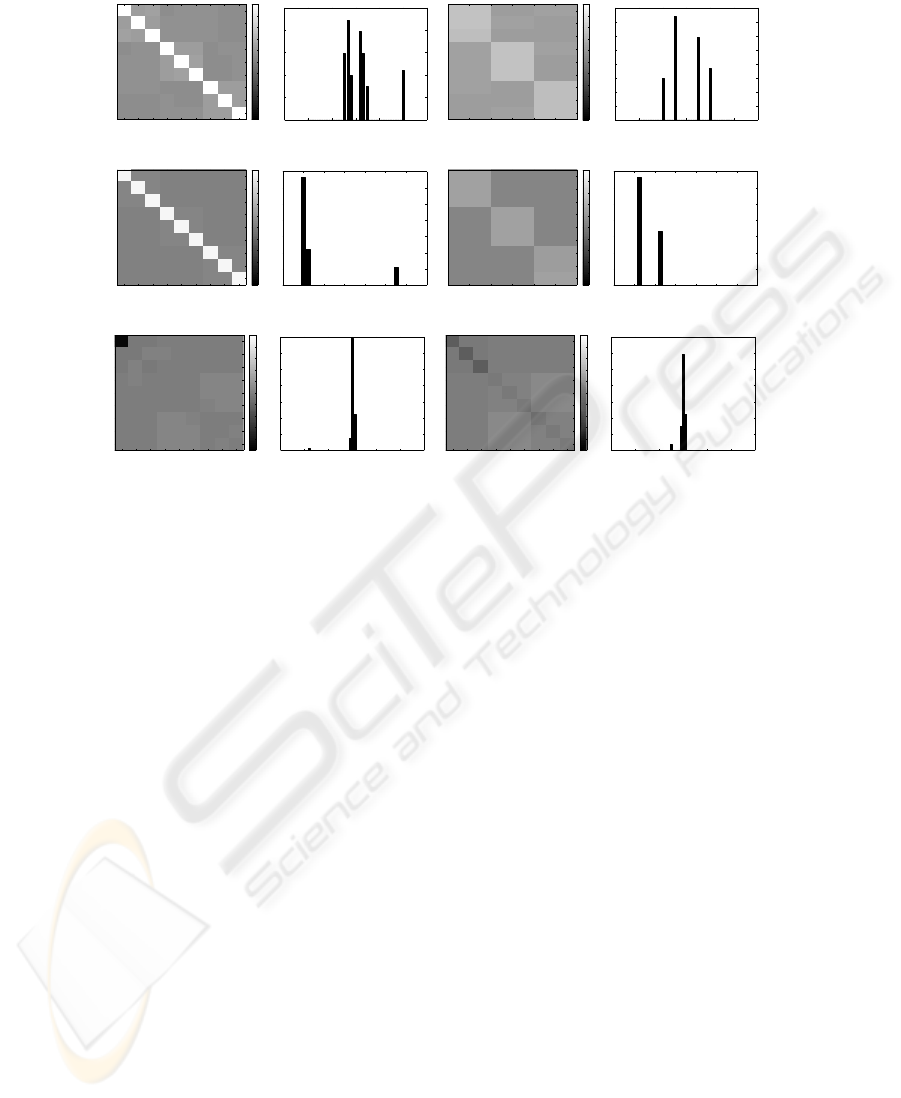
The ﬁrst artiﬁcial data set is based on an AND combination of 3 binary variables

deﬁning one of the 3 classes. Additional input variables are ﬁlled with random values.

Hence the intra-class variables are dependent on each other and their class label, but

independent to the other six input variables.

Figure 2 shows the empirical estimates and histograms of the correlation matrix,

the mutual information and the 3-way information interaction respectively for the unsu-

pervised (features towards features) and the supervised (features towards class labels)

case. In the both all dependence measures succeed in ﬁnding the 3 dependent intra-class

variables, but with differences in accuracy.

Correlation, for example, is constantly overestimating the dependencies, because

it shows no independence for the inter-class variables. Furthermore the knowledge of

positive or negative correlation seem of no use for information fusion, but only the ab-

solute magnitudes. Mutual information performs similarly in accuracy as information

interaction. So it ﬁnds the inter-class independence of the input variables as well as

the dependence of the intra-class variables. Finally, information interaction is giving

the most detailed information about the data’s structure. For the intra-class variables

it results in negative interaction, which indicates redundancy. The inter-class informa-

tion interactions are mostly zero and surprisingly it shows positive interactions, hence

synergy, between the blocks of intra-class variables, where we are not sure yet how to

explain this.

The second and more interesting artiﬁcial data set is based on the AND data set, but

now each input variable is replaced by its XOR combination of 2 variables. Overall it

has again 3 classes, where each depends now on 6 input variables. This new data set

2828

features

2 4 6 8 10 12 14 16 18

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(a) absolute correlation, zero-bar: 89%

classes

features

0.5 1 1.5 2 2.5 3 3.5

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(b) absolute correlation, zero-bar: 100%

features

2 4 6 8 10 12 14 16 18

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

classes

features

0.5 1 1.5 2 2.5 3 3.5

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(d) mutual information, zero-bar: 100%

features

2 4 6 8 10 12 14 16 18

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(e) 3-way interaction (fv

= 1) zero: 99%

features

2 4 6 8 10 12 14 16 18

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(f) 3-way interaction (cl = 1) zero: 94%

Fig.3. Unsupervised (a,c,e) / supervised (b,d,f) case for OR combined artiﬁcial data.

is a parity problem, which contains synergy between the XOR combined variables and

their class labels.

Figures 3(a),3(c) and 3(e) show the empirical estimates and the histograms for the

unsupervised case. Correlation ﬁnds independence between all variables except be-

tween the parity variables, where it results randomly in positiveor negative correlations.

Mutual information as well as the 3-way information interaction results show also only

the dependence between the parity variables. So none of the investigated dependence

measures ﬁnds all features that one class depends on in the unsupervised setting. We

hope to ﬁnd this hidden dependencies by investigating higher order information inter-

actions in future work.

The results of the supervised case, that are presented in the Figures 3(b),3(d) and

3(f), show a clear advantage of information interaction over the other two dependence

measures. Correlation and mutual information do not succeed in ﬁnding even the parity

variables, because they are based only on bivariate relationships. Whereas information

interaction ﬁnds synergy between the parity variables and detects all dependent vari-

ables of a class. As in the unsupervised case we hope to ﬁnd the intuitively expected

redundancies between the pairs of parity variables by regarding higher order informa-

tion interactions.

To summarize, it can be said that feature information interactions more accurately

describe complex dependence structures in data sets by giving their irreducible patterns.

This is especially true for parity problems. Furthermore it allows to differentiate feature

relationships into synergies and redundancies, which we feel is useful knowledge to

exploit in information fusion systems.

2929

features

100 200 300 400 500 600

100

200

300

400

500

600

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

p(x)

(a) correlation matrix, zero-bar: 37%

classes

features

2 4 6 8 10 12 14 16 18 20

100

200

300

400

500

600

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−1.5 −1 −0.5 0 0.5 1 1.5

0.05

0.1

0.15

0.2

0.25

0.3

0.35

p(x)

(b) correlation matrix, zero-bar: 30%

features

100 200 300 400 500 600

100

200

300

400

500

600

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

p(x)

classes

features

2 4 6 8 10 12 14 16 18 20

100

200

300

400

500

600

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.2 0 0.2 0.4 0.6 0.8 1 1.2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

p(x)

(d) mutual information, zero-bar: 68%

features

100 200 300 400 500 600

100

200

300

400

500

600

−0.1

−0.08

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

0.1

−0.2 −0.15 −0.1 −0.05 0 0.05 0.1 0.15

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(e) 3-way interaction (fv

= 1) zero: 95%

features

100 200 300 400 500 600

100

200

300

400

500

600

−0.1

−0.08

−0.06

−0.04

−0.02

0.02

0.04

0.06

0.08

0.1

−0.2 −0.15 −0.1 −0.05 0 0.05 0.1 0.15

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

p(x)

(f) 3-way interaction (cl = 1) zero: 93%

Fig.4. Unsupervised (a,c,e) / supervised (b,d,f) case for the Washington collection.

For the real data experiments we used the Washington collection, which consists

of 886 images annotated with 1 to 10 keywords and grouped into 20 classes. The ex-

tracted feature set consists of the global color and texture histogram which have 165

and 164 features respectively. Additionally we constructed of the term frequencies of

the keywords a textual feature vector of size 297.

This simple setting is in fact too simple to succeed with a classiﬁcation or retrieval

task. Intuitively global visual features and a handful of keywords are insufﬁcient to

discriminate any class. So we expect low relationships between the features in both: the

unsupervised case and the supervised.

Ignoring the class labels we ﬁrst investigated the feature dependencies for the unsu-

pervised setting. We calculated a sampled version of the 3-way information interaction,

where each sample consists of k = 3 random features out of the whole set. Figures

4(a),4(c) and 4(e) give the empirical estimates of the dependence measures and their

histograms. As expected the feature information interactions show only little depen-

dence in the feature set. Be aware that the interaction diagrams are scaled between

[−0.1, 0.1] compared to [−1, 1] for correlation and mutual information. So it is clearly

visible that the latter two, both 2-way dependence measures, indicate much higher re-

lationships (in number and magnitude) between the features. Hence one can state that

they also overestimate the feature’s dependencies for real data sets.

The results for the supervised setting are shown in Figures 4(b),4(d) and 4(f). Again

the scale of the information interaction diagrams is set to [−0.1, 0.1] for visibility rea-

sons. Here the correlation between the features and their class labels results in high de-

pendencies that are neither supported by the mutual information nor the 3-way feature

3030

information interaction. Mutual information overestimates as well a little the dependen-

cies.

Experiments that compare end-to-end classiﬁcation or retrieval results based on dif-

ferent feature selection or construction algorithms in multimedia problems have still to

be done in future work. Until then the usefulness of feature information interactions

in information fusion stays empirically unproven, but reasonable given that complex

feature relationships can be estimated reliably.

5 Conclusions and Future Work

The article reviews the formal theory and characteristics of feature information interac-

tion, an information-theoretic dependence measure. Through its stable and unambigu-

ous deﬁnition of feature relationships it can more accurately determine dependencies,

because e.g. redundant contributions to the overall relationships are not overcounted.

Interestingly, information interaction can have positiveand negativevalues, whereas

until now it is not completely clear how to consistently resolve the negative ones. Pos-

itive interactions are synergies, that should be exploited, for example, by complicating

the data model and using the feature’s joint evidence.

Experiments on artiﬁcial data, where the feature dependencies are known, under-

mine the theoretically claimed superior performance of information interactions over

bivariate dependence measures like correlation and mutual information especially for

parity problems. These ﬁndings in the controlled setting ﬁt also the tests on the real

data of the Washington collection. The ﬁnal prove of usefulness of feature information

interactions for information fusion in classiﬁcation or retrieval has to be done in future

work.

Other directions of research will be the utilization of more complex multimedia data

as e.g. the Wikipedia collection and tests with more sophisticated features like moment-

based visual features.

References

1. A. B. Benitez, S. F. Chang, Multimedia knowledge integration, summarization and evalua-

tion, Workshop on Multimedia Data Mining, 2002, pp. 23-26.

2. E. Bruno, N. Moenne-Loccoz, S. Marchand-Maillet, Design of multimodal dissimilarity

spaces for retrieval of multimedia documents, to appear in IEEE Transaction on Pattern Anal-

ysis and Machine Intelligence, 2008.

3. G. Chechik, N. Tishby, Extracting relevant structures with side information, Advances in

Neural Information Processing Systems, 15, 2003.

4. K. Tumer, J. Gosh, Linear order statistics combiners for pattern classiﬁcation, Combining

Artiﬁcial Neural Networks, 1999, 127–162.

5. L. Wu, P.R. Cohen, S.L. Oviatt, From members to team to committee - a robust approach to

gestural and multimodal recognition, Transactions on Neural Networks, 13(4), 2002, 972 -

982.

6. M. M. Kokar, J. Weyman, J.A. Tomasik, Formalizing classes of information fusion systems,

Information Fusion, 5, 2004, 189–202.

3131

7. N. Poh, S. Bengio, How do correlation and variance of base-experts affect fusion in biomet-

ric authentication tasks?, IEEE Transactions on Acoustics, Speech, and Signal Processing,

vol. 53, 2005, pp. 4384–4396.

8. R. Zhao, W. I. Grosky, Narrowing the semantic gap - improved text-based web document

retrieval using visual features, IEEE Trans. on Multimedia, 4(2), 2002, 189–200.

9. S. C. Dass, A. K. Jain, K. Nandakumar, A principled approach to score level fusion in multi-

modal biometric systems, Proc. of Audio- and Video-based Biometric Person Authentication

(AVBPA), 2005, pp. 1049–1058.

10. S. Wu, S. McClean, Performance prediction of data fusion for information retrieval, Infor-

mation Processing and Management, 42, 2006, 899–915.

11. D. M. Squire, W. Mller, H. Mller, and J. Raki, Content-based query of image databases,

inspirations from text retrieval: inverted ﬁles, frequency-based weights and relevance feed-

back, in the 10th Scandinavian Conference on Image Analysis (SCIA’99), (Kangerlussuaq,

Greenland), 1999, pp. 143–149.

12. T. Kolenda, O. Winther, L.K. Hansen, J. Larsen, Independent component analysis for under-

standing multimedia content, Neural Networks for Signal Processing, 2002, 757– 766.

13. T. Westerveld, A. P. de Vries, Multimedia retrieval using multiple examples, In International

Conference on Image and Video Retrieval (CIVR’04), 2004, 344-352.

14. Y. Wu, K. Chen-Chuan Chang, E. Y. Chang and J. R. Smith, Optimal multimodal fusion for

multimedia data analysis, MULTIMEDIA ’04: Proc. of the 12th annual ACM international

conference on Multimedia, ACM Press, 2004, pp. 572–579.

15. R. Yan, A. G. Hauptmann, The combination limit in multimedia retrieval, MULTIMEDIA

’03: Proceedings of the eleventh ACM international conference on Multimedia, ACM Press,

2003, pp. 339–342.

16. A. Vinokurow, D.R. Hardoon and J. Shawe-Taylor, Learning the Semantics of Multime-

dia Content with Application to Web Image Retrieval and Classiﬁcation, in Proceedings

of Fourth International Symposium on Independent Component Analysis and Blind Source

Separation, Nara, Japan, 2003.

17. A. Jakulin, I. Bratko, Quantifying and Visualizing Attribute Interactions, ArXiv Computer

Science e-prints, Provided by the Smithsonian/NASA Astrophysics Data System, 2003.

18. A. Jakulin, I. Bratko, Analyzing Attribute Dependencies, Proc. of Principles of Knowledge

Discovery in Data (PKDD), 2838, 2003, 229–240.

19. A. Hyvarinen, E. Oja, Independent Component Analysis: Algorithms and Applications, Neu-

ral Networks, 2000, 13(4-5),pp. 411-430.

20. N. Vasconcelos, G. Carneiro, What is the Role of Independence for Visual Recognition?,

European Conference on Computer Vision, Copenhagen, 2002, 297 - 311.

21. I. Nemenman, Information theory, multivariate dependence and genetic networks, eprint

arXiv:q-bio/0406015, ARXIV, 2004.

22. M.J. Pazzani, Searching for Dependencies in Bayes Classiﬁers, 1996, Learning from Data:

AI and Statistics, Springer Verlag.

23. A.J. Bell, The Co-Information Lattice, 4th Int. Symposium on Independent Component Anal-

ysis and blind Signal Seperation (ICA2003), 2003, pp. 921–926.

24. T. Westerveld and R. van Zwol, Multimedia Retrieval at INEX 2006, 2007, ACM SIGIR

Forum, 41(1), pp. 58-63.

25. I. Kononenko, E. Simec and M. Robnik-Sikonja, Overcoming the myopia of inductive learn-

ing algorithms with RELIEFF, Applied Intelligence, 7(1), 1997, pp. 39-55, Springer Nether-

lands.

26. I. Perez, Learning in presence of complex attribute interactions: An Approach Based on

Relational Operators, PhD dissertation, University of Illinois at Urbana-Champaign, 1997.

3232

27. K. Jajuga and D. Papla, Copula Functions in Model Based Clustering, in Studies in Classiﬁ-

cation, Data Analysis, and Knowledge Organization, Part 15, 2006, Springer Berlin Heidel-

berg.

28. T. Liu, Z. Chen, B. Zhang, W. Ma and G. Wu, Improving Text Classiﬁcation using Local La-

tent Semantic Indexing, Fourth IEEE International Conference on Data Mining (ICDM’04),

pp. 162-169, 2004.

3333